Multi-Physical Models of Bending Characteristics on the Double-Clamped Beam Switch for Flexible Electronic Devices Application
Abstract
1. Introduction
2. Modeling
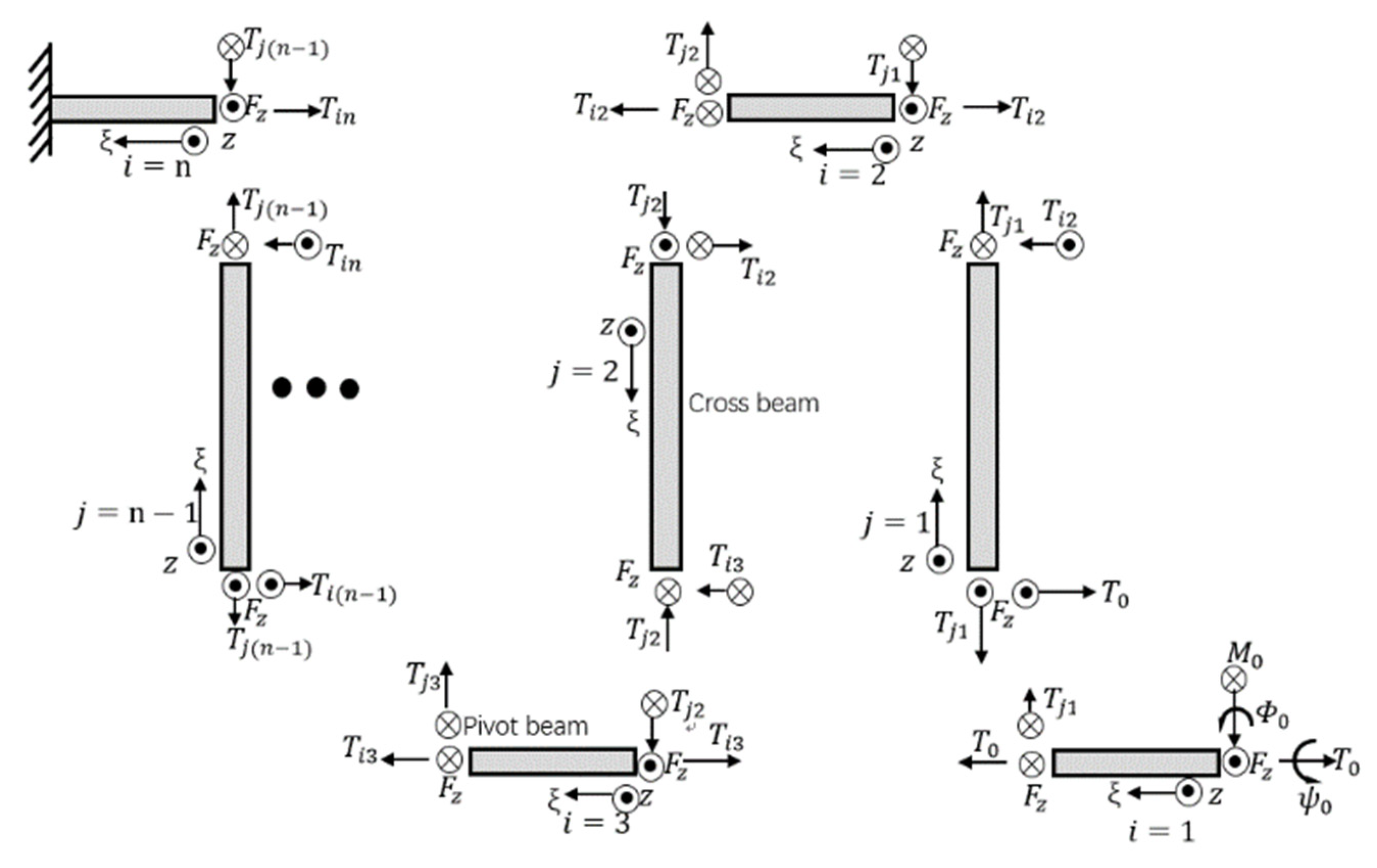
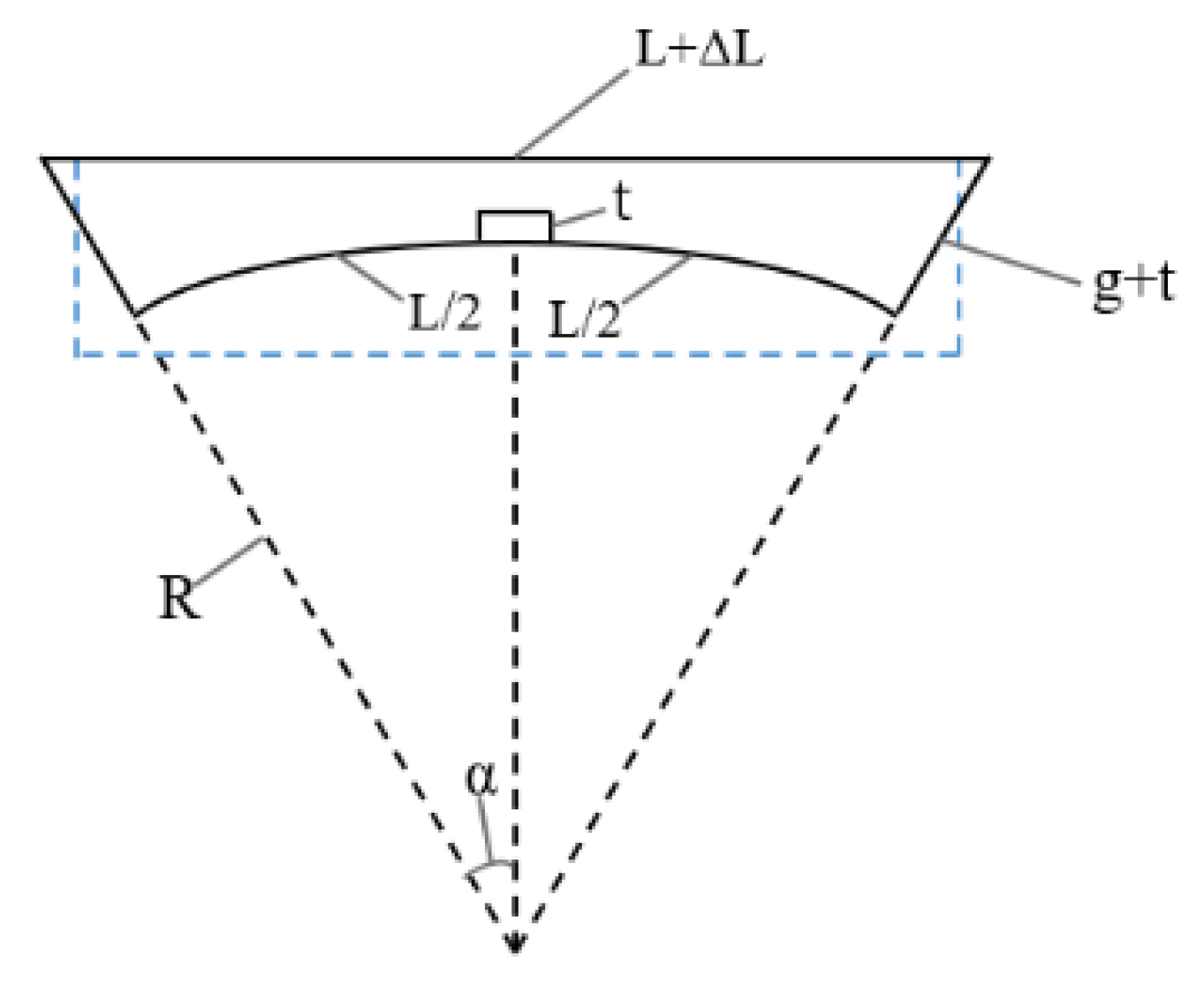
2.1. Static Model of Bending Characteristics
2.2. Dynamic Model of Bending Characteristics
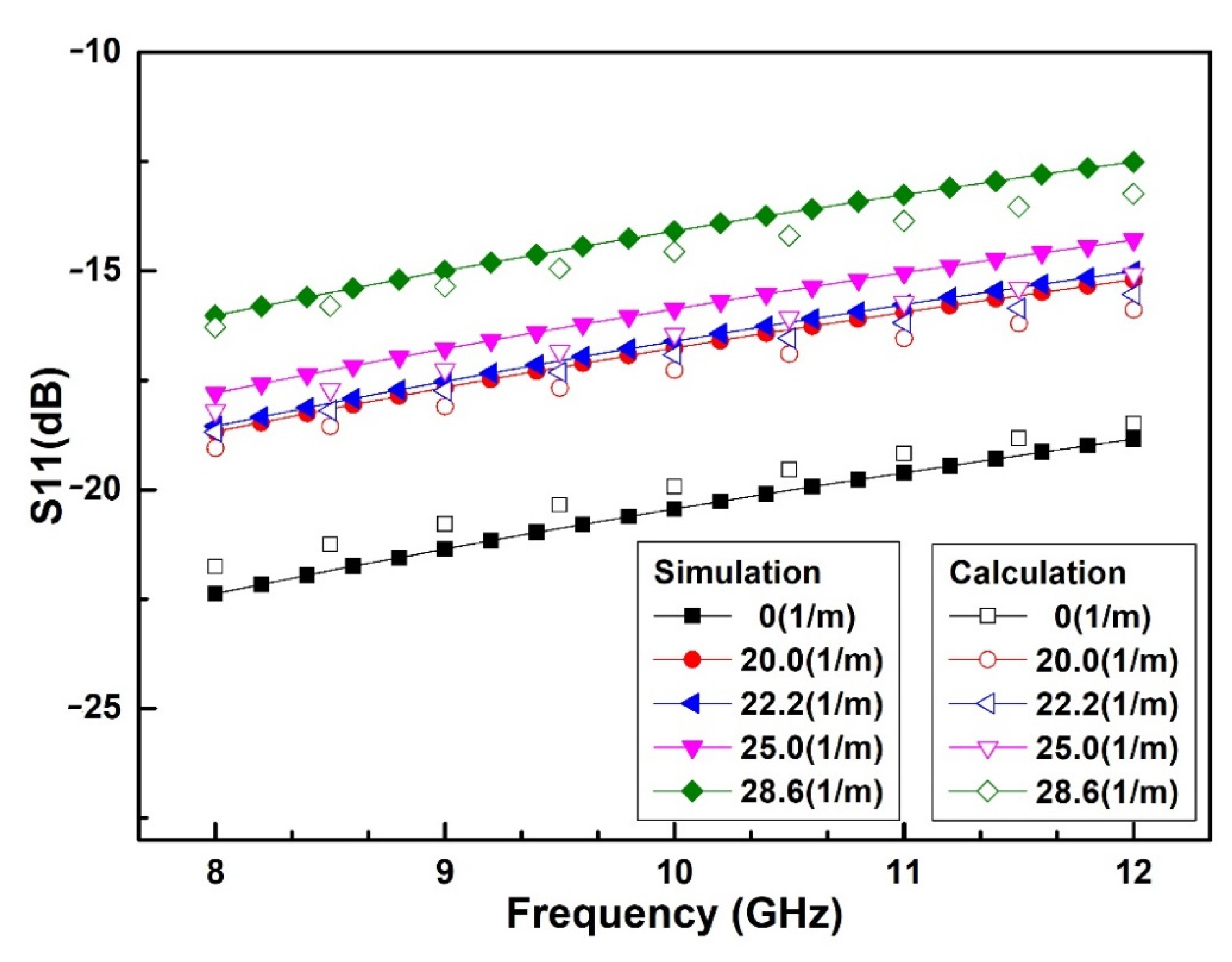
2.3. Microwave Model of Bending Characteristics
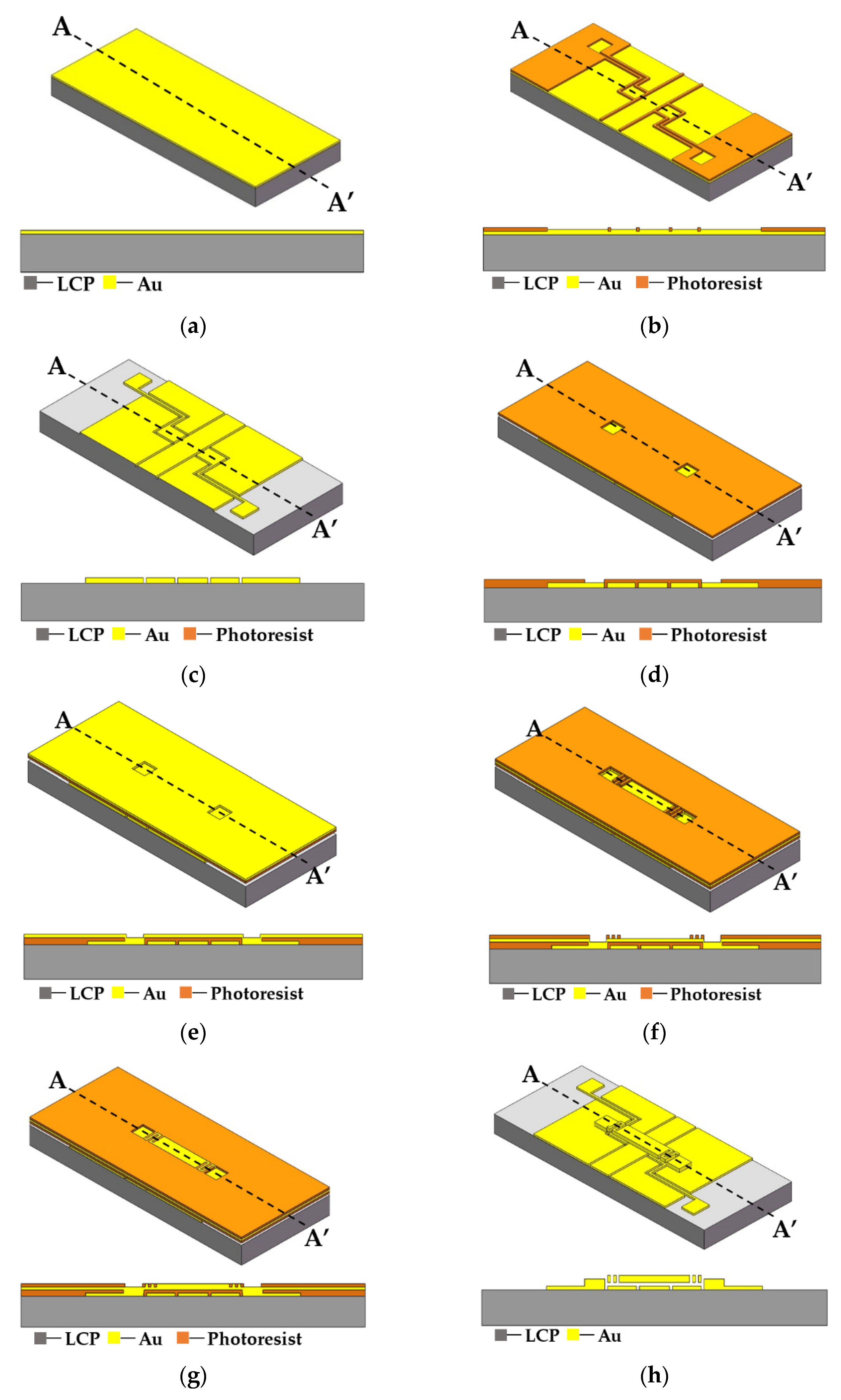
3. Design and Fabrication
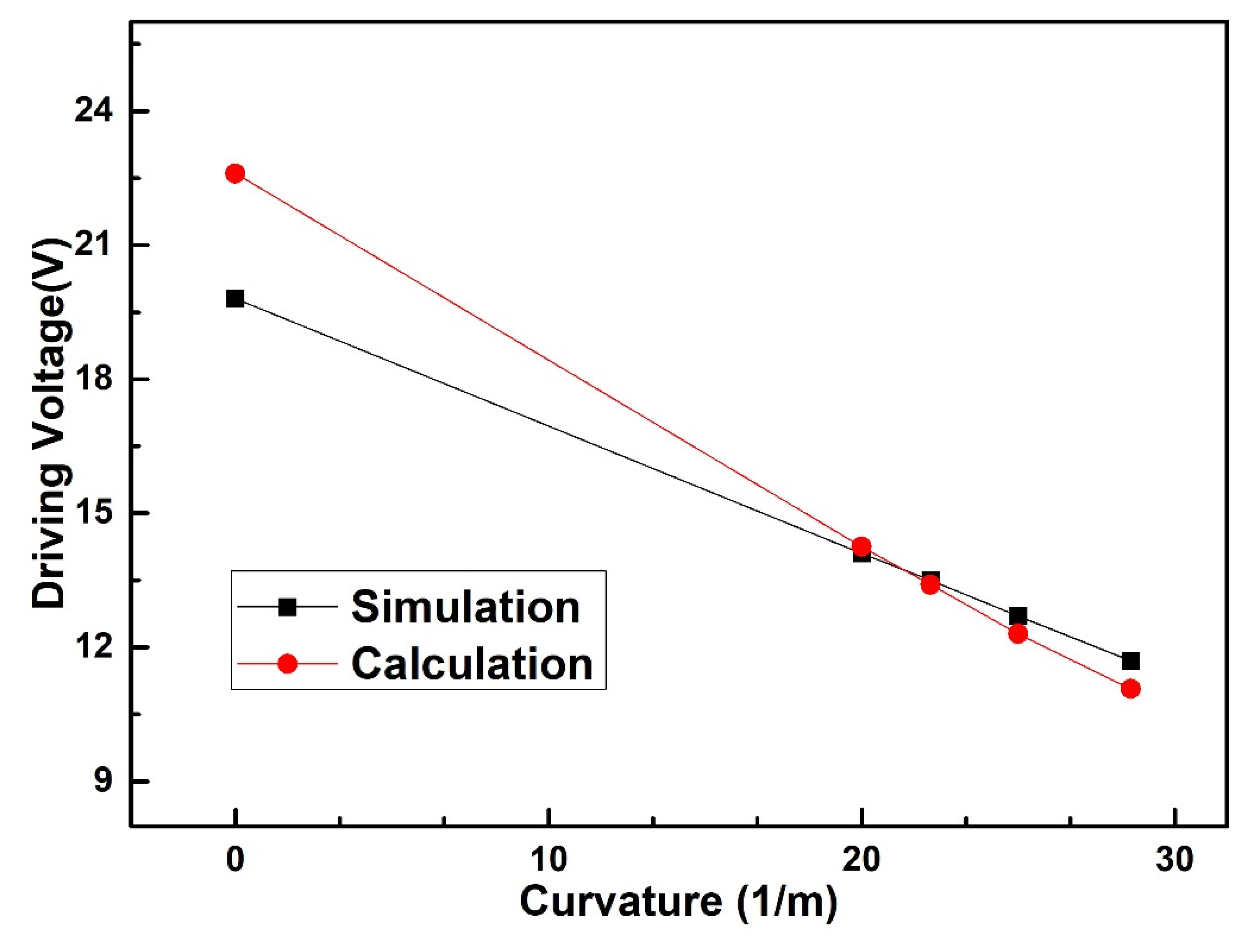
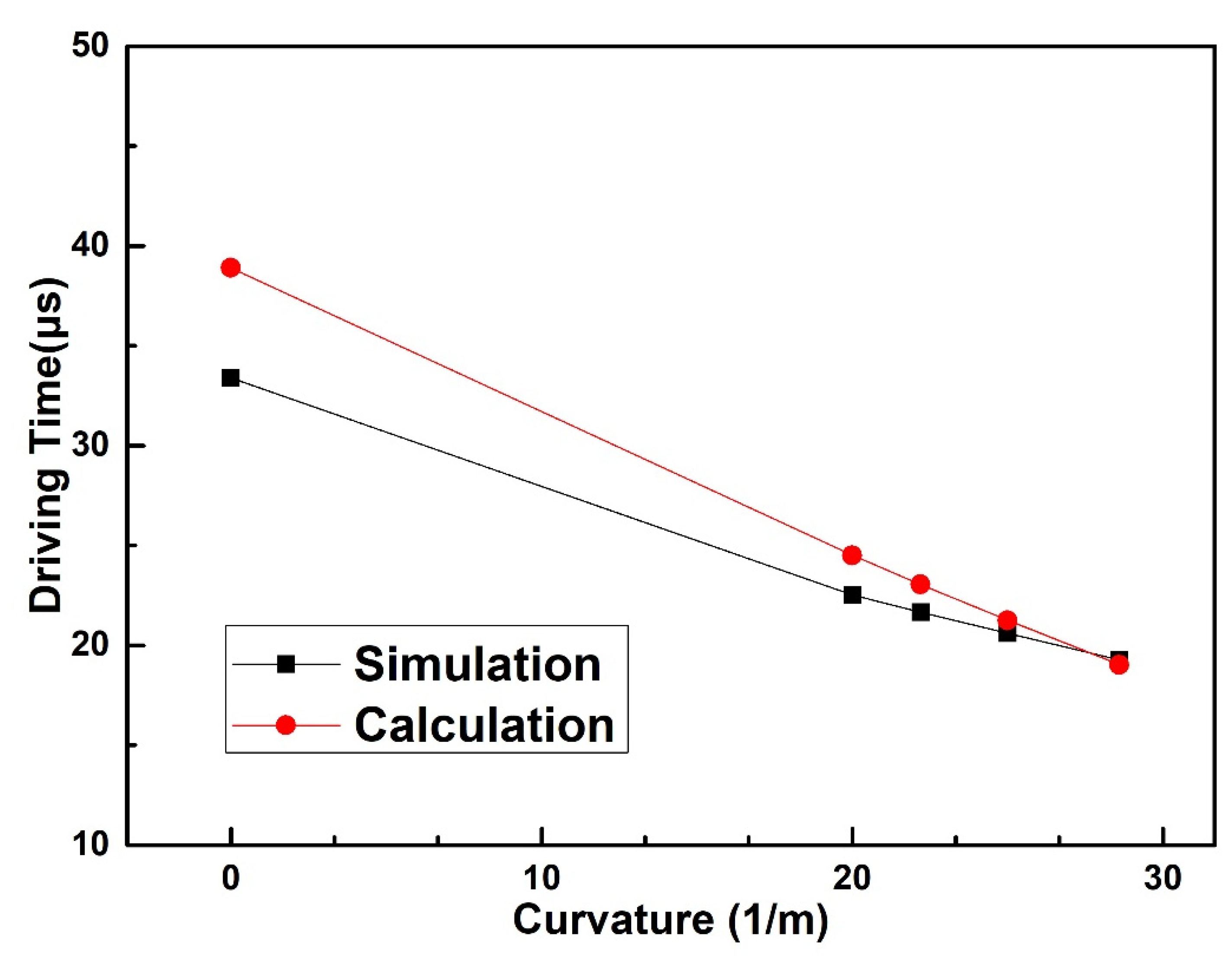
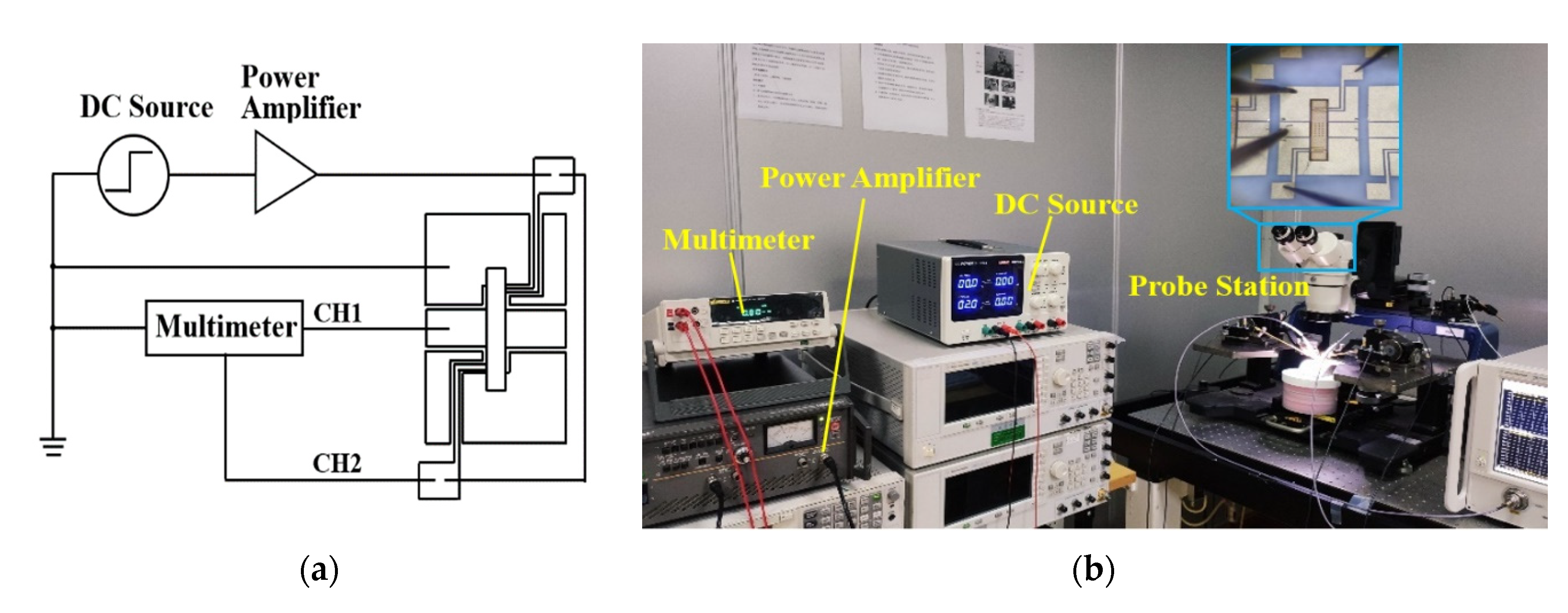
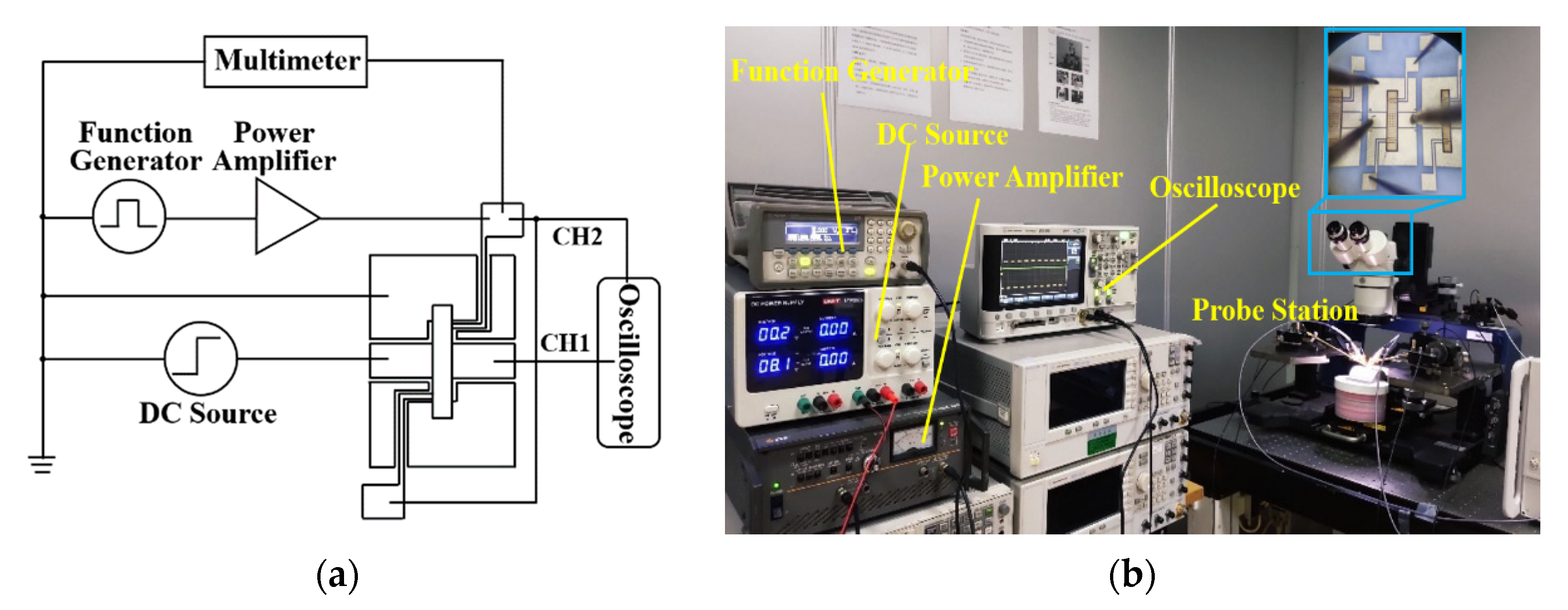
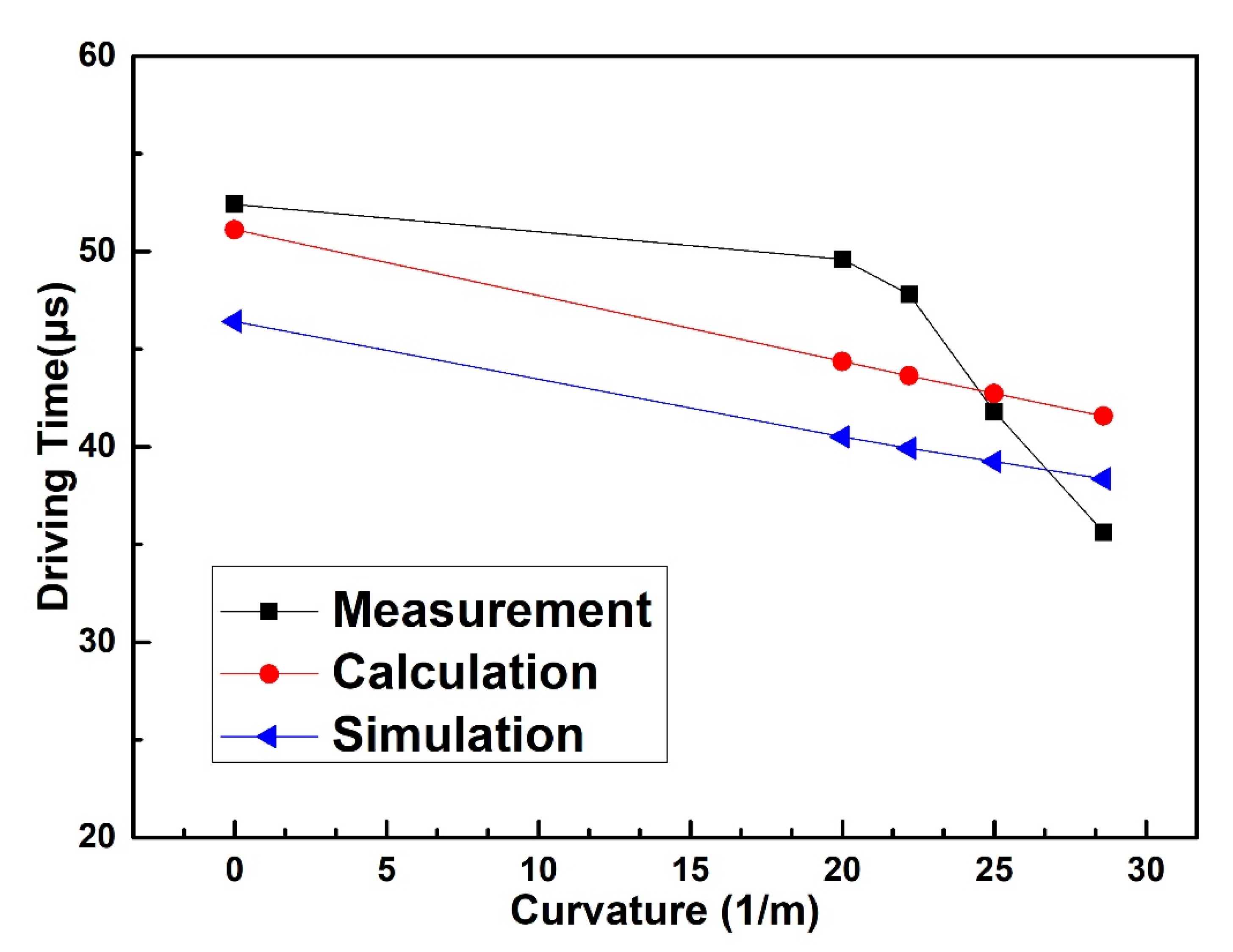
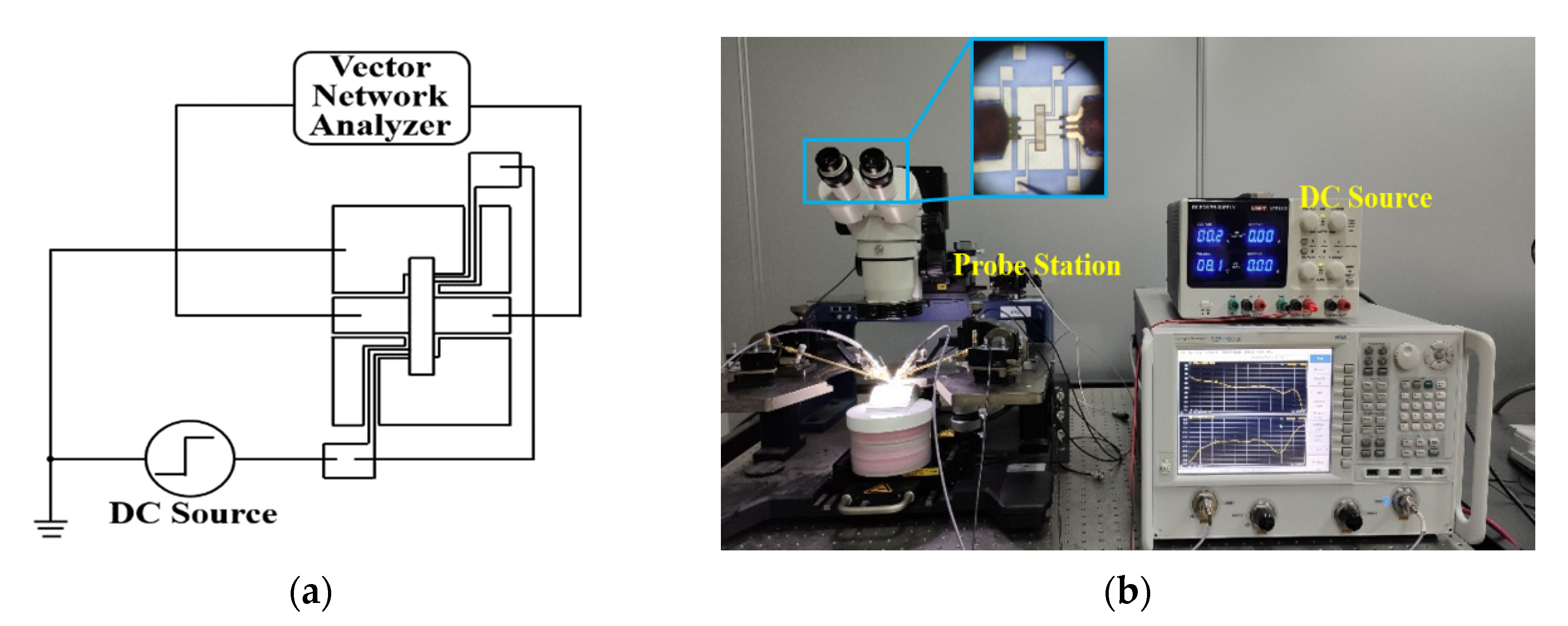
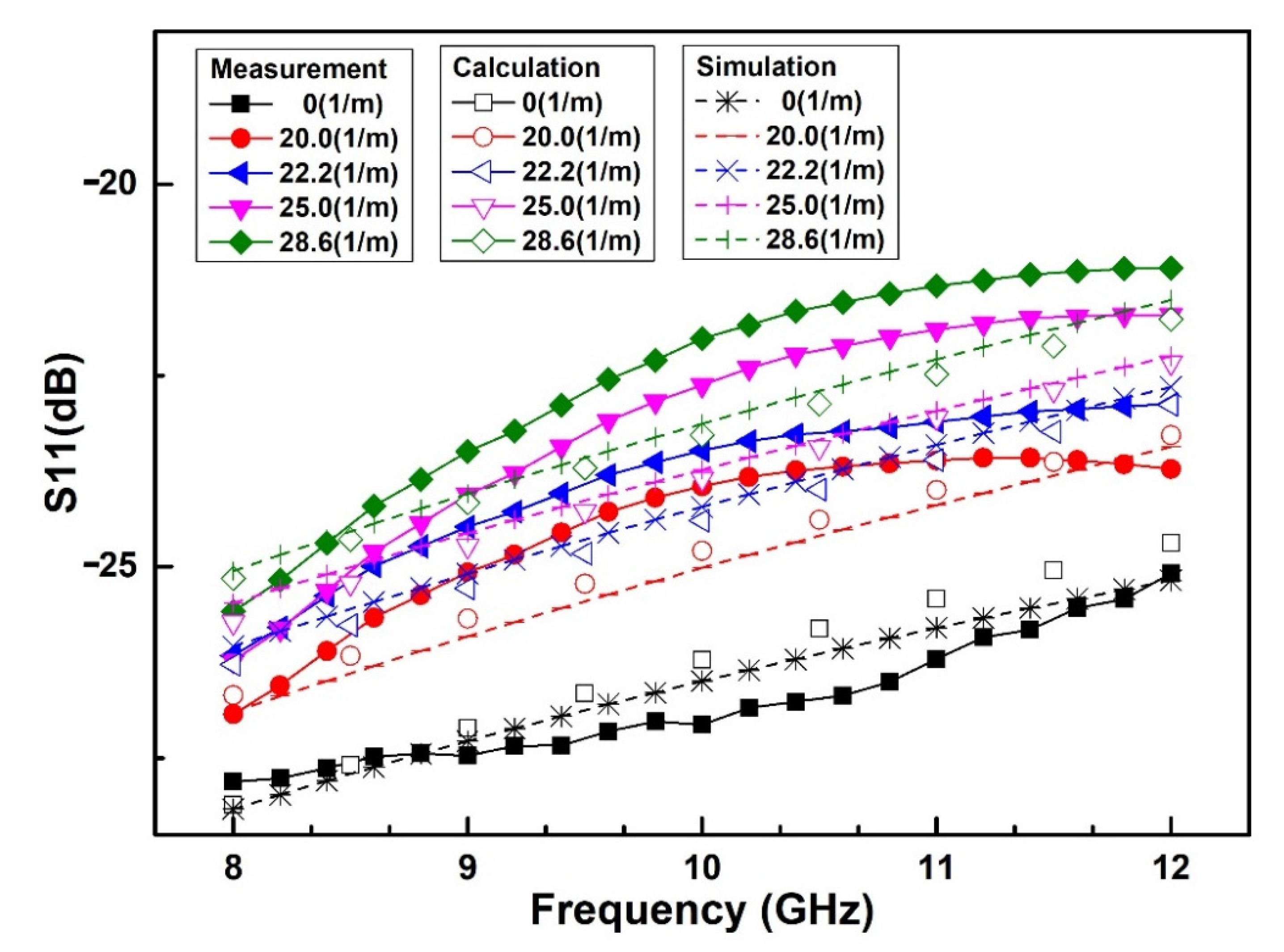
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jiang, Y.; Zhang, M.L.; Duan, X.X.; Zhang, H.; Pang, W. A flexible, gigahertz, and free-standing thin film piezoelectric MEMS resonator with high figure of merit. Appl. Phys. Lett. 2017, 111, 023505. [Google Scholar] [CrossRef]
- Fujishiro, A.; Takahashi, S.; Sawada, K.; Ishida, M.; Kawano, T. Flexible neural electrode arrays with switch-matrix based on a planar silicon process. IEEE Electron. Device Lett. 2014, 35, 253–255. [Google Scholar] [CrossRef]
- Xu, Y. Post-CMOS and post-MEMS compatible flexible skin technologies: A review. IEEE Sens. J. 2013, 13, 3962–3975. [Google Scholar] [CrossRef]
- Lu, J.; Nakano, Y.; Takagi, H.; Maeda, R. High-efficient chip to wafer self-alignment and bonding applicable to MEMS-IC flexible integration. IEEE Sens. J. 2013, 13, 651–656. [Google Scholar] [CrossRef]
- Griesbach, T.; Wurz, M.C.; Rissing, L. Design, fabrication, and testing of a modular magnetic field microsensor on a flexible polymer foil. IEEE Trans. Magn. 2012, 48, 3843–3846. [Google Scholar] [CrossRef]
- Cerveri, P.; Quinzi, M.; Bovio, D.; Frigo, C.A. A novel wearable apparatus to measure fingertip forces in manipulation tasks based on MEMS barometric sensors. IEEE Trans. Haptics 2017, 10, 317–324. [Google Scholar] [CrossRef]
- Guo, Y.; Schütz, S.; Vaghi, A.; Li, Y.-H.; Guo, Z.Q.; Chang, F.-K.; Barrettino, D.; Wang, S.X. Stand-alone stretchable absolute pressure sensing system for industrial applications. IEEE Trans. Ind. Electron. 2017, 64, 8739–8746. [Google Scholar] [CrossRef]
- Kim, J.; Seo, D.G.; Cho, Y.-H. A flexible skin piloerection monitoring sensor. Appl. Phys. Lett. 2014, 104, 253502. [Google Scholar] [CrossRef]
- Bock, K. Polymer electronics systems—Polytronics. Proc. IEEE 2005, 93, 1400–1406. [Google Scholar] [CrossRef]
- Gaikwad, A.M.; Steingart, D.A.; Ng, T.N.; Schwartz, D.E.; Whiting, G.L. A flexible high potential printed battery for powering printed electronics. Appl. Phys. Lett. 2013, 102, 233302. [Google Scholar] [CrossRef]
- Wang, X.F.; Engel, J.; Liu, C. Liquid crystal polymer (LCP) for MEMS: Processes and applications. J. Micromech. Microeng. 2003, 13, 628–633. [Google Scholar] [CrossRef]
- Kang, Y.R.; Kang, S.C.; Paek, K.K.; Kim, Y.K.; Kim, S.W.; Ju, B.K. Air-gap type film bulk acoustic resonator using flexible thin substrate. Sens. Actuat. A-Phys. 2005, 117, 62–70. [Google Scholar] [CrossRef]
- Petroni, S.; Maruccio, G.; Guido, F.; Amato, M.; Campa, A.; Passaseo, A.; Todaro, M.T.; De Vittorio, M. Flexible piezoelectric cantilevers fabricated on polyimide substrate. Microelectron. Eng. 2012, 98, 603–606. [Google Scholar] [CrossRef]
- Coutts, G.M.; Mansour, R.R.; Chaudhuri, S.K. A MEMS-tunable frequency-selective surface monolithically integrated on a flexible substrate. In Proceedings of the 2007 IEEE/MIT-S International Microwave Symposium, Honolulu, HI, USA, 3–8 June 2007. [Google Scholar]
- Kingsley, N.; Papapolymerou, J. Organic “Wafer-Scale” packaged miniature 4-bit RF MEMS phase shifter. IEEE Trans. Microw. Theory Tech. 2006, 54, 1229–1236. [Google Scholar] [CrossRef]
- Kingsley, N.; Ponchak, G.E.; Papapolymerou, J. Reconfigurable RF MEMS phased array antenna integrated within a liquid crystal polymer (LCP) System-on-Package. IEEE Trans. Antennas Propag. 2008, 56, 108–118. [Google Scholar] [CrossRef]
- Wang, G.; Thompson, D.; Tentzeris, E.M.; Papapolymerou, J. Low cost RF MEMS switches using LCP substrate. In Proceedings of the 34th European Microwave Conference, Amsterdam, The Netherlands, 12–14 October 2004; pp. 1441–1444. [Google Scholar]
- Zhang, Q.X.; Yu, A.B.; Guo, L.H.; Kumar, R.; Teoh, K.W.; Liu, A.Q.; Lo, G.Q.; Kwong, D.L. Development of RF MEMS switch on flexible organic substrate with wafer transfer technology (WTT). In Proceedings of the 56th Electronic Components and Technology Conference 2006, San Diego, CA, USA, 30 May–2 June 2006. [Google Scholar]
- Patil, S.B.; Chu, V.; Conde, J.P. Performance of thin film silicon MEMS on flexible plastic substrates. Sens. Actuat. A-Phys. 2008, 144, 201–206. [Google Scholar] [CrossRef]
- Pestana, T.G.; Pinto, R.M.R.; Dias, R.A.; Martins, M.; Chu, V.; Gaspar, J.; Conde, J.P. Fabrication and characterization of thin-film silicon resonators on 10 μm-thick polyimide substrates. J. Micromech. Microeng. 2020, 30, 045007. [Google Scholar] [CrossRef]
- Hatem, S.; Fehmi, N.; Slim, C. Dynamic study of a capacitive MEMS switch with double clamped-clamped microbeams. Shock Vib. 2014, 2014, 807489. [Google Scholar]
- Persano, A.; Quaranta, F.; Martucci, M.C.; Siciliano, P.; Cola, A. On the electrostatic actuation of capacitive RF MEMS switches on GaAs substrate. Sens. Actuat. A-Phys. 2015, 232, 202–207. [Google Scholar] [CrossRef]
- Pertin, O. Kurmendra Pull-in-voltage and RF analysis of MEMS based high performance capacitive shunt switch. Microelectron. J. 2018, 77, 5–15. [Google Scholar] [CrossRef]
- Han, L.; Gao, X.F. Modeling of bending characteristics on micromachined RF MEMS switch based on LCP substrate. IEEE Trans. Electron Devices 2016, 63, 3707–3712. [Google Scholar] [CrossRef]
- Rebeiz, G.M. RF MEMS: Theory, Design, and Technology; John Wiley & Sons Inc.: New York, NY, USA, 2004; pp. 50–62. [Google Scholar]
- Goran, S.; Ljiljana, Z.; Mirjana, D. Novel efficient methods for inductance calculation of meander inductor. COMPEL 2006, 25, 916–928. [Google Scholar]
- Fang, Y.M.; Li, P. A pull-in model for parallel-plate electrostatically MEMS actuators with the fringing field effect. Chin. J. Sens. Actuat. 2011, 24, 848–852. [Google Scholar]



| Material | Au | LCP |
|---|---|---|
| Resistivity ρ (μΩ·cm) | 2.35 | N/A |
| Thermal conductivity κ (W/cm·K) | 3.18 | 0.002 |
| Thermal expansion coefficient α (×10−6/K) | 14.2 | 17 |
| Young’s modulus E (GPa) | 78 | 2.225 |
| Density δ (kg/m3) | 19,300 | 1400 |
| Specific heat capacity C (J/kg·K) | 128 | 1340 |
| Poisson’s ratio | 0.42 | 0.49 |
| Item | Size (μm) |
|---|---|
| Width of the beam | 100 |
| Length of the beam | 600 |
| Thickness of the beam | 2.5 |
| Width of the driving electrode | 100 |
| Length of the driving electrode | 155 |
| Thickness of the driving electrode | 2 |
| Gap between the original beam and driving electrode | 3 |
| Item | Size (μm) |
|---|---|
| Width of the beam | 140 |
| Length of the beam | 650 |
| Thickness of the beam | 2.4 |
| Gap between the original beam and driving electrode | 10.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, L.; Chen, L.; Qin, R.; Wang, K.; Zhang, Z.; Nie, M.; Huang, X. Multi-Physical Models of Bending Characteristics on the Double-Clamped Beam Switch for Flexible Electronic Devices Application. Sensors 2020, 20, 7074. https://doi.org/10.3390/s20247074
Han L, Chen L, Qin R, Wang K, Zhang Z, Nie M, Huang X. Multi-Physical Models of Bending Characteristics on the Double-Clamped Beam Switch for Flexible Electronic Devices Application. Sensors. 2020; 20(24):7074. https://doi.org/10.3390/s20247074
Chicago/Turabian StyleHan, Lei, Lijun Chen, Ruijie Qin, Kang Wang, Zhiqiang Zhang, Meng Nie, and Xiaodong Huang. 2020. "Multi-Physical Models of Bending Characteristics on the Double-Clamped Beam Switch for Flexible Electronic Devices Application" Sensors 20, no. 24: 7074. https://doi.org/10.3390/s20247074
APA StyleHan, L., Chen, L., Qin, R., Wang, K., Zhang, Z., Nie, M., & Huang, X. (2020). Multi-Physical Models of Bending Characteristics on the Double-Clamped Beam Switch for Flexible Electronic Devices Application. Sensors, 20(24), 7074. https://doi.org/10.3390/s20247074




