Gyro-Sensor-Based Vibration Control for Dynamic Humanoid-Robot Walking on Inclined Surfaces
Abstract
:1. Introduction
- Proposal of a gyro-sensor-based feedback-control system to control the ankle-pitch and hip-pitch motors of the robot for stable walking on inclined surfaces, as indicated in Figure 1. The control system enables the robot to walk stably on a downslope surface of inclination up to 10.2°. The feedback controller is easy to implement in a commercial, low-cost, mass-produced, and open-source hardware platform that can be integrated easily into a light-weight humanoid robot (see Section 2).
- The ankle-pitch and hip-pitch motors play a significant role in posture stabilization [15,19]. Therefore, initially for smaller surface inclinations, the ankle-pitch motor is controlled and for larger surface inclinations both ankle-pitch and hip-pitch motors are controlled. This reduces the computational complexity compared to the inverse-kinematics-based approaches in the conventional ZMP-based control [18,19,48] (see Section 2).
- The angular-pitch velocity of the robot is considered to be a characteristic of the robot-gait, is measured by the gyro sensor for the walking robot and is analyzed in the frequency domain. A novel use of the Fourier analysis for the angular-pitch velocity is proposed to determine the cause of postural instability on inclined surfaces. Moreover, the effect of the feedback gain on the robot gait on inclined surfaces is analyzed (see Section 2 and Section 3).
- Experimental observation, which increased the friction between robot feet and inclined surface reduces the robot vibrations at larger surface inclinations. The results of robot-walking experiments with increased friction represents an optimization approach for the feedback gain to reduce vibrations in the robot at increased surface inclinations (see Section 4).
- The IPM, used to model the robot walking, is extended for inclined surfaces. An additional gyro-sensor-based feedback loop is included in the model to explain the Fourier response of the angular-pitch velocity. Further, the IPM is extended to include the nonlinearity, induced by the surface inclination, to explain the harmonics observed in the Fourier transform of the angular-pitch velocity (see Section 5).
2. Robot-Walking Experiments
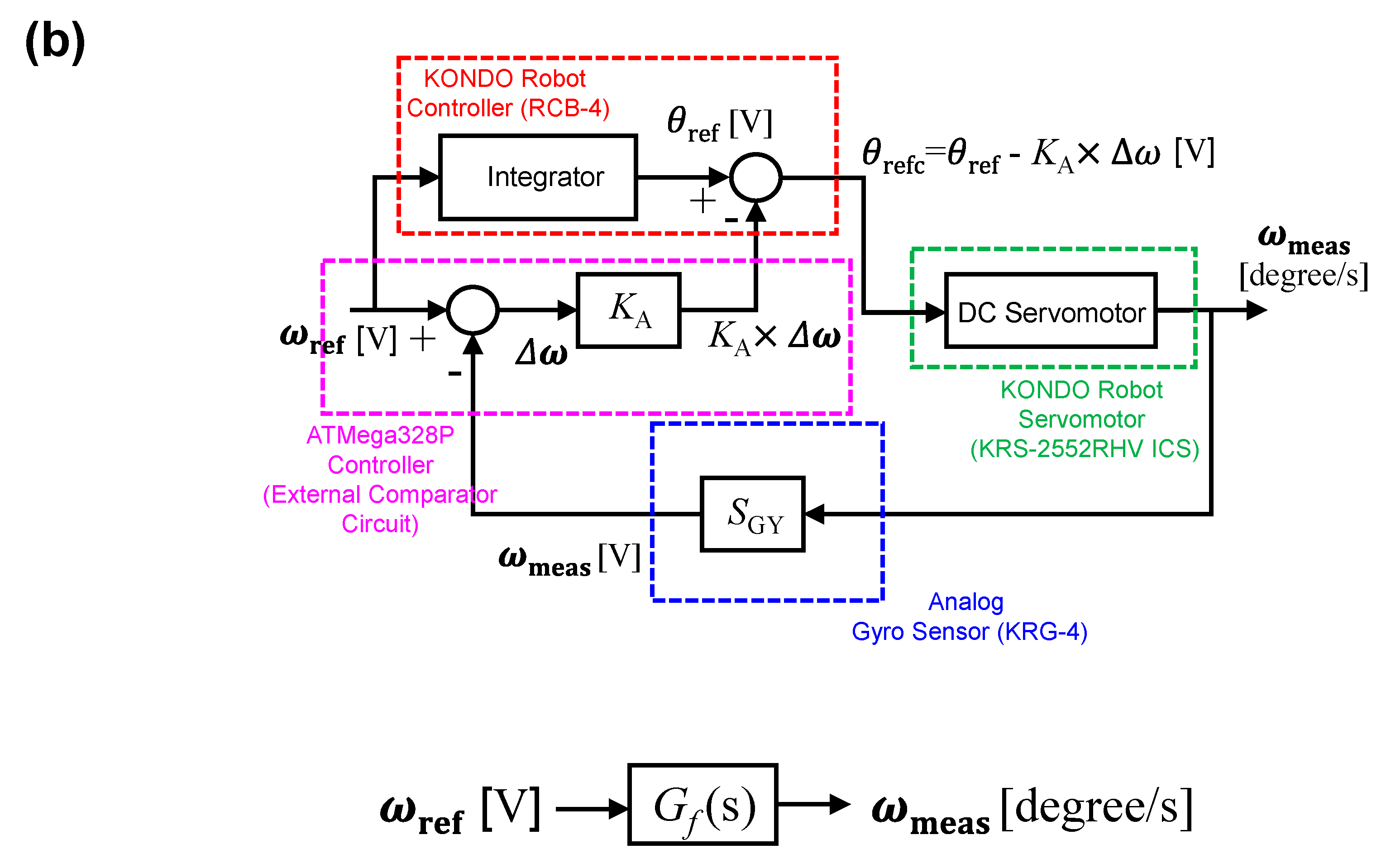
2.1. Motor Control System
2.2. Experimental Setup
- The robot is walking on the inclined surfaces without any gyro-sensor-based feedback control, until it becomes unstable beyond a critical inclination φcr0.
- Beyond the critical inclination φcr0, the ankle-pitch motor (MA) is controlled by the gyro-sensor feedback. This allows the robot to walk up to a higher critical surface inclination φcr1. The robot becomes unstable beyond φcr1.
- The hip-pitch motor (MH) is controlled by the gyro-sensor feedback in addition to the ankle motor. This enables the robot to walk stably on inclined surfaces above the critical surface inclination φcr1.
2.3. Robot-Gait Implementation
2.4. Experimental Results
3. Analysis of Experimental Results
4. Experiments with Robot-Foot Friction
5. Model Development for Robot Balancing
5.1. Inverted Pendulum Model for Robot Walking
5.2. Robot-Walking-Model Extension to Inclined Surfaces
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Eaton, R.; Katupitiya, J.; Siew, K.W.; Howarth, B. Autonomous farming: Modeling and control of agricultural machinery in a unified framework. In Proceedings of the 15th International Conference on Mechatronics and Machine Vision Practice, Auckland, New Zealand, 2–4 December 2008; Volume 1, pp. 499–504. [Google Scholar]
- Cheein, F.A.A.; Carelli, R. Agricultural robotics: Unmanned robotic service units in agricultural tasks. IEEE Ind. Electron. Mag. 2013, 7, 48–581. [Google Scholar] [CrossRef]
- Michael, N.; Fink, J.; Kumar, V. Cooperative manipulation and transportation with aerial robots. Auton. Robot. 2011, 30, 73–86. [Google Scholar] [CrossRef] [Green Version]
- Burri, M.; Nikolic, J.; Hürzeler, C.; Caprari, G.; Siegwart, R. Aerial service robots for visual inspection of thermal power plant boiler systems. In Proceedings of the 2nd International Conference on Applied Robotics for the Power Industry (CARPI), Zurich, Switzerland, 11–13 September 2012; pp. 70–75. [Google Scholar]
- Casper, J.; Murphy, R.R. Human-robot interactions during the robot-assisted urban search and rescue response at the World Trade Center. IEEE Trans. Syst. Man. Cybern. B 2003, 33, 138–153. [Google Scholar] [CrossRef] [Green Version]
- Holt, M.; Campbell, R.J.; Nikitin, M.B. Fukushima Nuclear Disaster; Congressional Research Service: Washington, DC, USA, 2012. [Google Scholar]
- Yoshida, T.; Nagatani, K.; Tadokoro, S.; Nishimura, T.; Koyanagi, E. Improvements to the Rescue Robot Quince Toward Future Indoor Surveillance Missions in the Fukushima Daiichi Nuclear Power Plant. In Field and Service Robotics; Springer Tracts in Advanced Robotics; Yoshida, K., Tadokoro, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; pp. 19–32. [Google Scholar]
- Hirai, K.; Hirose, M.; Haikawa, Y.; Takenaka, T. The development of Honda humanoid robot. In Proceedings of the IEEE International Conference on Robotics and Automation, Leuven, Belgium, 16–20 May 1998; pp. 1321–1326. [Google Scholar]
- Kaneko, K.; Harada, K.; Kanehiro, F.; Miyamori, G.; Akachi, K. Humanoid robot HRP-3. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22—26 September 2008; pp. 2471–2478. [Google Scholar]
- Kaneko, K.; Kaminaga, H.; Sakaguchi, T.; Kajita, S.; Morisawa, M.; Kumagai, I.; Kanehiro, F. Humanoid Robot HRP-5P: An electrically actuated humanoid robot with high-power and wide-range joints. IEEE Robot. Autom. Lett. 2019, 4, 1431–1438. [Google Scholar] [CrossRef]
- Pratt, G.; Manzo, J. The DARPA robotics challenge [competitions]. IEEE Robot. Autom. Mag. 2013, 20, 10–12. [Google Scholar] [CrossRef]
- Hornung, A.; Wurm, K.M.; Bennewitz, M. Humanoid robot localization in complex indoor environments. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 1690–1695. [Google Scholar]
- Kuindersma, S.; Deits, R.; Fallon, M.; Valenzuela, A.; Dai, H.; Permenter, F.; Koolen, T.; Marion, P.; Tedrake, R. Optimization-based locomotion planning, estimation, and control design for the atlas humanoid robot. Auton. Robot. 2016, 40, 429–455. [Google Scholar] [CrossRef]
- Dai, H.; Tedrake, R. Planning robust walking motion on uneven terrain via convex optimization. In Proceedings of the IEEE-RAS 16th International Conference on Humanoid Robots (Humanoids), Cancun, Mexico, 15–17 November 2016; pp. 579–586. [Google Scholar]
- Hemami, H.; Weimer, F.; Koozekanani, S. Some aspects of the inverted pendulum problem for modeling of locomotion systems. IEEE Trans. Automat. Contr. 1973, 18, 658–661. [Google Scholar] [CrossRef]
- Kajita, S.; Tani, K. Study of dynamic biped locomotion on rugged terrain-derivation and application of the linear inverted pendulum mode. In Proceedings of the IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; pp. 1405–1411. [Google Scholar]
- Kajita, S.; Kanehiro, F.; Kaneko, K.; Yokoi, K.; Hirukawa, H. The 3D Linear Inverted Pendulum Mode: A simple modeling for a biped walking pattern generation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Maui, HI, USA, 29 October–3 November 2001; pp. 239–246. [Google Scholar]
- Vukobratovic, M.; Borovac, B. Zero-Moment Point-Thirty Five Years of Its Life. Int. J. Hum. Robot. 2004, 1, 157–173. [Google Scholar] [CrossRef]
- Kajita, S.; Hirukawa, H.; Harada, K.; Yokoi, K. Introduction to Humanoid Robotics; Springer: Berlin Heidelberg, Germany, 2014; pp. 45–65, 69–97. [Google Scholar]
- Regier, P.; Milioto, A.; Stachniss, C.; Bennewitz, M. Classifying obstacles and exploiting class information for humanoid navigation through cluttered environments. Int. J. Humanoid Robot. 2020, 17, 2050013. [Google Scholar] [CrossRef]
- Wahrmann, D.; Hildebrandt, A.C.; Bates, T.; Wittmann, R.; Sygulla, F.; Seiwald, P.; Rixen, D. Vision-based 3d modeling of unknown dynamic environments for real-time humanoid navigation. Int. J. Humanoid Robot. 2019, 16, 1950002. [Google Scholar] [CrossRef]
- Nguyen, Q.; Agrawal, A.; Martin, W.; Geyer, H.; Sreenath, K. Dynamic bipedal locomotion over stochastic discrete terrain. Int. J. Robot Res. 2018, 37, 1537–1553. [Google Scholar] [CrossRef]
- Morisawa, M.; Kajita, S.; Kanehiro, F.; Kaneko, K.; Miura, K.; Yokoi, K. Balance control based on capture point error compensation for biped walking on uneven terrain. In Proceedings of the 12th IEEE-RAS International Conference on Humanoid Robots, Osaka, Japan, 29 November–1 December 2012; pp. 734–740. [Google Scholar]
- Sygulla, F.; Rixen, D. A force-control scheme for biped robots to walk over uneven terrain including partial footholds. Int. J. Adv. Robot. Syst. 2020, 17, 1–14. [Google Scholar] [CrossRef]
- Chew, C.M.; Pratt, J.; Pratt, G. Blind walking of a planar bipedal robot on sloped terrain. In Proceedings of the IEEE International Conference on Robotics and Automation, Detroit, MI, USA, 10–15 May 1999; pp. 381–386. [Google Scholar]
- Hidaka, Y.; Nishizawa, K.; Nenchev, D.N. Dynamic stepping on unknown obstacles with upper-body compliance and angular momentum damping from the reaction null-space. In Proceedings of the International Conference on Robotics and Automation, Montreal, QC, Canada, 20–24 May 2019; pp. 5273–5279. [Google Scholar]
- Fevre, M.; Goodwine, B.; Schmiedeler, J.P. Terrain-blind walking of planar underactuated bipeds via velocity decomposition-enhanced control. Int. J. Robot Res. 2019, 38, 1307–1323. [Google Scholar] [CrossRef]
- KHR-3HV Ver.2 with Li-Fe Battery, Kondo Kagaku Co. Ltd. 2019. Available online: https://kondo-robot.com/product/03110e (accessed on 26 November 2020).
- Ayyappa, E. Normal human locomotion, part 1: Basic concepts and terminology. J. Prosthet. Orthot. 1997, 9, 10–17. [Google Scholar] [CrossRef]
- Ayyappa, E. Normal human locomotion, part 2: Motion, ground-reaction force and muscle activity. JPO J. Prosthet. Orthot. 1997, 9, 49–57. [Google Scholar] [CrossRef]
- Schneider, E.; Chao, E.Y. Fourier analysis of ground reaction forces in normals and patients with knee joint disease. J. Biomech. 1983, 16, 591–601. [Google Scholar] [CrossRef]
- Chao, E.Y.; Laughman, R.K.; Schneider, E.; Stauffer, R.N. Normative data of knee joint motion and ground reaction forces in adult level walking. J. Biomech. 1983, 16, 219–233. [Google Scholar] [CrossRef]
- Giakas, G.; Baltzopoulos, V. Time and frequency domain analysis of ground reaction forces during walking: An investigation of variability and symmetry. Gait. Posture. 1997, 5, 189–197. [Google Scholar] [CrossRef]
- Crowe, A.; Schiereck, P.; De Boer, R.W.; Keessen, W. Characterization of human gait by means of body center of mass oscillations derived from ground reaction forces. IEEE Trans. Biomed. Eng. 1995, 42, 293–303. [Google Scholar] [CrossRef]
- Crowe, A.; Schiereck, P.; de Boer, R.; Keessen, W. Characterization of gait of young adult females by means of body centre of mass oscillations derived from ground reaction forces. Gait. Posture. 1993, 1, 61–68. [Google Scholar] [CrossRef]
- Wurdeman, S.R.; Huisinga, J.M.; Filipi, M.; Stergiou, N. Multiple sclerosis affects the frequency content in the vertical ground reaction forces during walking. Clin. Biomech. 2011, 26, 207–212. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tafazzoli, F.; Safabakhsh, R. Model-based human gait recognition using leg and arm movements. Eng. Appl. Artif. Intel. 2010, 23, 1237–1246. [Google Scholar] [CrossRef]
- Suzuki, K.; Imai, H.; Kawamura, Y.; Sankai, Y. Gait control of human and humanoid on irregular terrain considering interaction with environment. In Proceedings of the IEEE International Workshop on Robot and Human Interactive Communication, Millbrae, CA, USA, 31 October–2 November 2003; pp. 277–284. [Google Scholar]
- Bötzel, K.; Olivares, A.; Cunha, J.P.; Sáez, J.M.G.; Weiss, R.; Plate, A. Quantification of gait parameters with inertial sensors and inverse kinematics. J. Biomech. 2018, 72, 207–214. [Google Scholar] [CrossRef] [PubMed]
- Cela, A.; Yebes, J.J.; Arroyo, R.; Bergasa, L.M.; Barea, R.; López, E. Complete Low-Cost Implementation of a Teleoperated Control System for a Humanoid Robot. Sensors 2013, 13, 1385–1401. [Google Scholar] [CrossRef] [Green Version]
- Gyro Sensor KRG-4, Kondo Kagaku Co. Ltd. 2019. Available online: https://kondo-robot.com/product/03003 (accessed on 26 November 2020).
- Morimoto, J.; Endo, G.; Nakanishi, J.; Cheng, G. A biologically inspired biped locomotion strategy for humanoid robots: Modulation of sinusoidal patterns by a coupled oscillator model. IEEE Trans. Robot. 2008, 24, 185–191. [Google Scholar] [CrossRef]
- Khan, U.I.; Chen, Z. Natural Oscillation and Optimal Gaits for Humanoid Biped Models. In Proceedings of the IEEE-RAS International Conference on Humanoid Robots, Beijing China, 6–9 November 2018; pp. 196–201. [Google Scholar]
- Kajita, S.; Asano, F.; Mitsuharu, M.; Miura, K.; Kaneka, K.; Kanehiro, F.; Kazuhito, Y. Vertical vibration suppression for a position controlled biped robot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 1629–1634. [Google Scholar]
- Cheng, C.; Chang, J.; Lv, W.; Li, K.; Li, Z.; Yuan, C.; Ma, S. Frequency-Temporal Disagreement Adaptation for Robotic Terrain Classification via Vibration in a Dynamic Environment. Sensors 2020, 20, 6550. [Google Scholar] [CrossRef]
- Liu, H.; Cui, S.; Liu, Y.; Ren, Y.; Sun, Y. Design and Vibration Suppression Control of a Modular Elastic Joint. Sensors 2018, 18, 1869. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.-Y.; Park, I.-W.; Oh, J.-H. Walking Control Algorithm of Biped Humanoid Robot on Uneven and Inclined Floor. J. Intel. Robot. Syst. 2007, 48, 457–484. [Google Scholar] [CrossRef] [Green Version]
- Joe, H.-M.; Oh, J.-H. A Robust Balance-Control Framework for the Terrain-Blind Bipedal Walking of a Humanoid Robot on Unknown and Uneven Terrain. Sensors 2018, 18, 1869. [Google Scholar] [CrossRef] [Green Version]
- KRS-2552RHV ICS Servomotor, Kondo Kagaku Co. Ltd. 2019. Available online: https://kondo-robot.com/product/03067e (accessed on 27 November 2020).
- PIC16F690. Available online: https://www.microchip.com/wwwproducts/en/PIC16F690 (accessed on 27 November 2020).
- RCB-4HV Board, Kondo Kagaku Co. Ltd. 2019. Available online: https://kondo-robot.com/product/03076 (accessed on 12 December 2020).
- Ogata, K.; Yang, Y. Modern Control Engineering; Prentice hall: Upper Saddle River, NJ, USA, 2010; pp. 27–29. [Google Scholar]
- Corke, P. Robotics, Vision and Control: Fundamental Algorithms in MATLAB® Second, Completely Revised; Springer: Berlin/Heidelberg, Germany, 2017; Volume 118, pp. 251–257. [Google Scholar]
- Siciliano, B.; Sciavicco, L.; Villani, L.; Oriolo, G. Robotics: Modelling, Planning and Control; Springer Science & Business Media: Berlin, Germany, 2010; pp. 198–209. [Google Scholar]
- Scarpino, M. Motors for Makers: A Guide to Steppers, Servos, and Other Electrical Machines; Que Publishing: Seattle, WA, USA, 2015; pp. 78–85. [Google Scholar]
- Urrea, C.; Kern, J. A new model for analog servo motors. Simulations and experimental results. Can. J. Automat. Contr. Intel. Syst. 2011, 2, 29–38. [Google Scholar]
- Wada, T.; Ishikawa, M.; Kitayoshi, R.; Maruta, I.; Sugie, T. Practical modeling and system identification of R/C servo motors. In Proceedings of the IEEE Control Applications & Intelligent Control, St. Petersburg, Russia, 8–10 July 2009; pp. 1378–1383. [Google Scholar]
- Sakai, F.; Kamiya, Y.; Seki, H.; Hikizu, M. Dynamic Characteristics of DC Servo Motor Driven by Conventional Servo Driver-Estimation of Circuit Constants in Conventional Servo Driver. J. Japan Soc. Precis. Eng. 2000, 66, 266–271. [Google Scholar] [CrossRef] [Green Version]
- Atmel, “ATmega328P: 8-bit AVR Microcontroller”. 2015. Available online: https://www.microchip.com/wwwproducts/en/ATmega328P (accessed on 29 November 2020).
- Ellis, G. Control System Design Guide, 4th ed.; Butterworth-Heinemann: Waltham, MA, USA, 2012; pp. 364–366. [Google Scholar]
- Cannon, R.H. Dynamics of Physical Systems; Courier Corporation: Chelmsford, MA, USA, 2003; pp. 171–172. [Google Scholar]
- Li, Z.; Zhou, C.; Tsagarakis, N.; Caldwell, D. Compliance control for stabilizing the humanoid on the changing slope based on terrain inclination estimation. Auton. Robot. 2016, 40, 955–971. [Google Scholar] [CrossRef] [Green Version]
- Loney, S.L. Plane Trigonometry; Cambridge University Press: London, UK, 1893; pp. 87–88. [Google Scholar]
- Euler, L. De novo genere oscillationum. Commentarii Academiae Scientiarum Petropolitanae 1750, 11, 128–149. [Google Scholar]
- Euler, L. The Rational Mechanics of Flexible or Elastic Bodies: Introduction to Vol. X and XI; Springer Science & Business Media: Berlin, Germany, 1960; pp. 1638–1788. [Google Scholar]
- Von Helmholtz, H. On the Sensations of Tone as a Physiological Basis for the Theory of Music, 2nd ed.; Longmans: London, UK, 1885; pp. 411–413. [Google Scholar]
- Strutt, J.W.; Rayleigh, B. The Theory of Sound; Dover: Downers Grove, IL, USA, 1945; pp. 74–84. [Google Scholar]
- Duffing, G. Forced Oscillations with Variable Natural Frequency and Their Technical Significance; Vieweg & Sohn: Berlin, Germany, 1918. [Google Scholar]
- Kovacic, I.; Brennan, M.J. The Duffing Equation: Nonlinear Oscillators and Their Behavior; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 28–29. [Google Scholar]
- Spong, M.W. The swing up control problem for the acrobot. IEEE Control Syst. Mag. 1995, 15, 49–55. [Google Scholar]
- Nijmeijer, H.; Berghuis, H. On Lyapunov control of the Duffing equation. IEEE Trans. Circuits Syst. I. Fundam. Theory Appl. 1995, 42, 473–477. [Google Scholar] [CrossRef]
- Sandberg, I.W. On the response of nonlinear control systems to periodic input signals. Bell Syst. Tech. J. 1964, 43, 911–926. [Google Scholar] [CrossRef]















| Parameter | Unit | Amount |
|---|---|---|
| Height | m | 0.4 |
| Height of COM | m | 0.3 |
| Length of foot | m | 0.03 |
| Mass + | kg | 1.5 |
| Degrees of Freedom * | - | 17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dutta, S.; Miura-Mattausch, M.; Ochi, Y.; Yorino, N.; Mattausch, H.J. Gyro-Sensor-Based Vibration Control for Dynamic Humanoid-Robot Walking on Inclined Surfaces. Sensors 2020, 20, 7139. https://doi.org/10.3390/s20247139
Dutta S, Miura-Mattausch M, Ochi Y, Yorino N, Mattausch HJ. Gyro-Sensor-Based Vibration Control for Dynamic Humanoid-Robot Walking on Inclined Surfaces. Sensors. 2020; 20(24):7139. https://doi.org/10.3390/s20247139
Chicago/Turabian StyleDutta, Sunandan, Mitiko Miura-Mattausch, Yoshihiro Ochi, Naoto Yorino, and Hans Jürgen Mattausch. 2020. "Gyro-Sensor-Based Vibration Control for Dynamic Humanoid-Robot Walking on Inclined Surfaces" Sensors 20, no. 24: 7139. https://doi.org/10.3390/s20247139
APA StyleDutta, S., Miura-Mattausch, M., Ochi, Y., Yorino, N., & Mattausch, H. J. (2020). Gyro-Sensor-Based Vibration Control for Dynamic Humanoid-Robot Walking on Inclined Surfaces. Sensors, 20(24), 7139. https://doi.org/10.3390/s20247139






