Consideration of Thermo-Vacuum Stability of a MEMS Gyroscope for Space Applications
Abstract
:1. Introduction
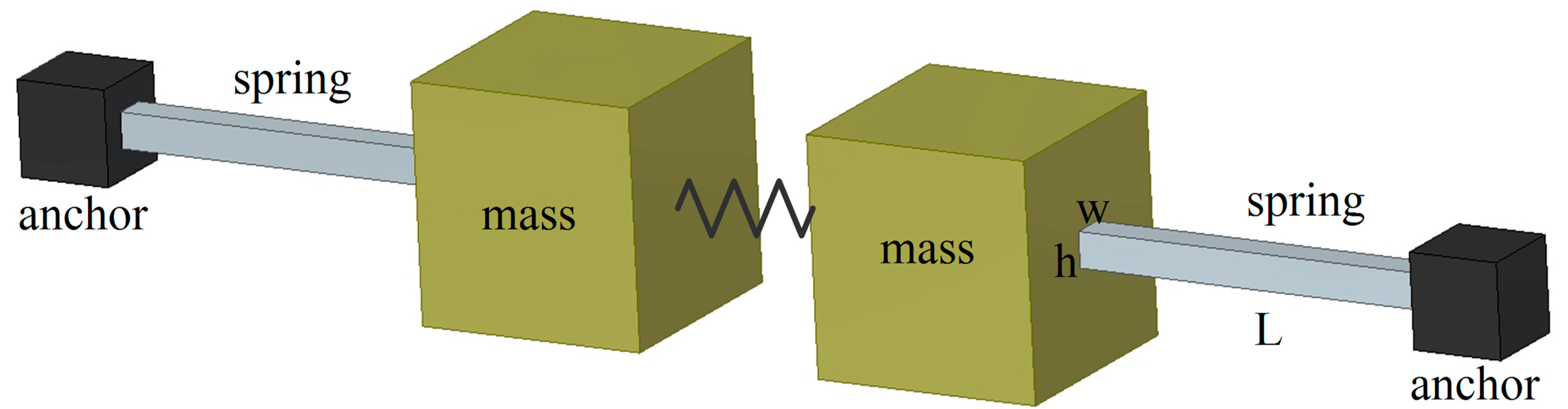
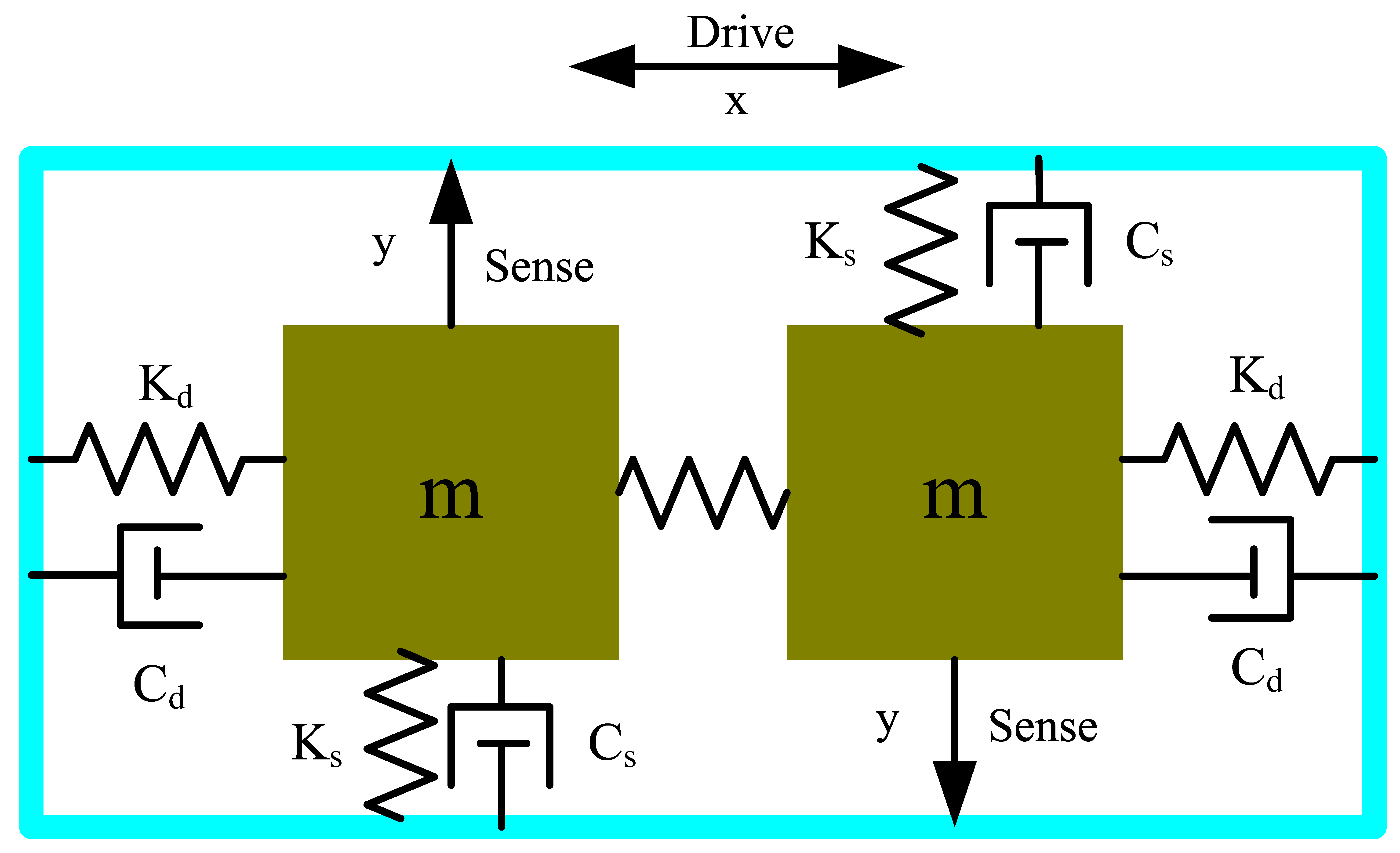
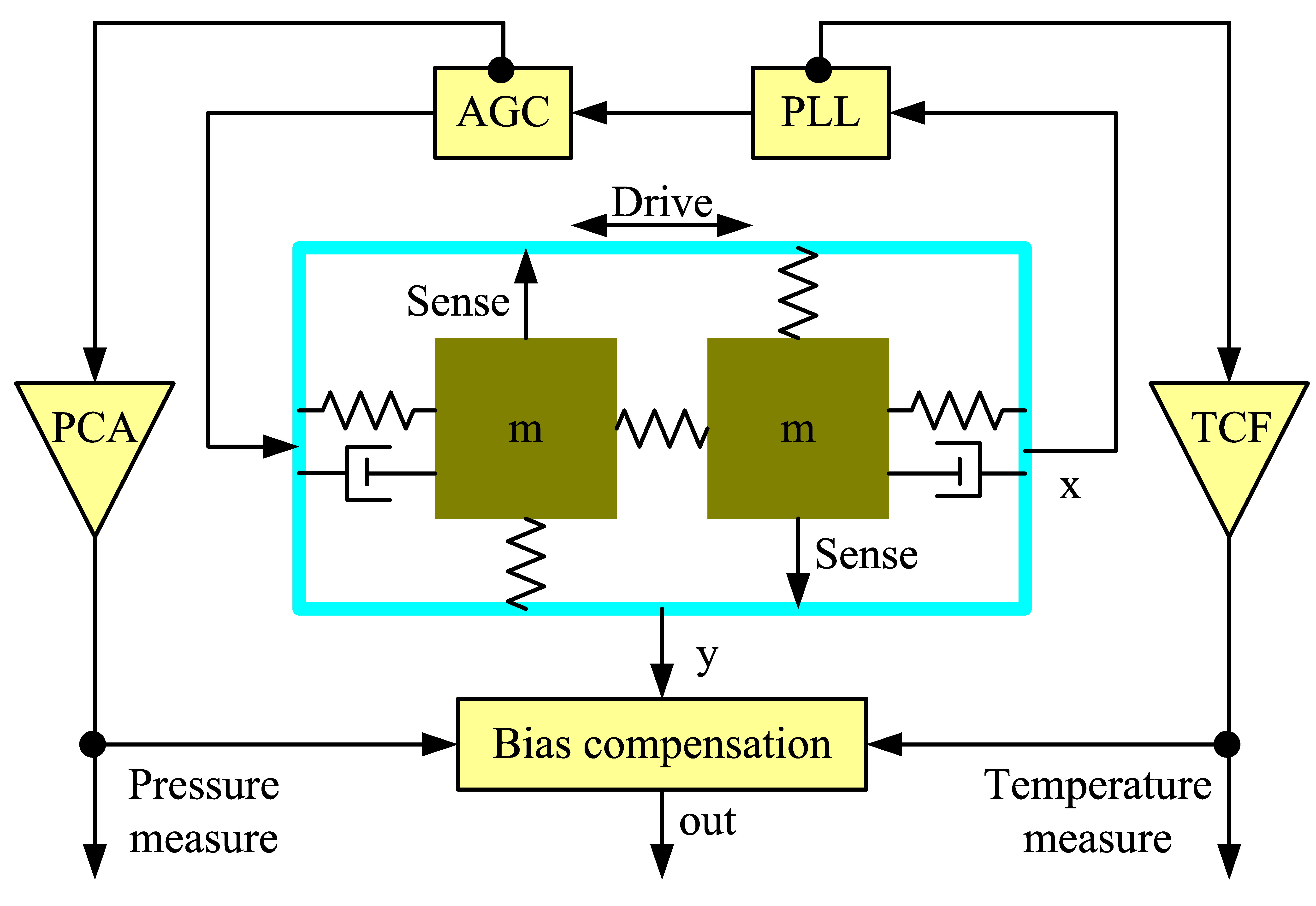
2. Bias Drift Analysis and Compensation
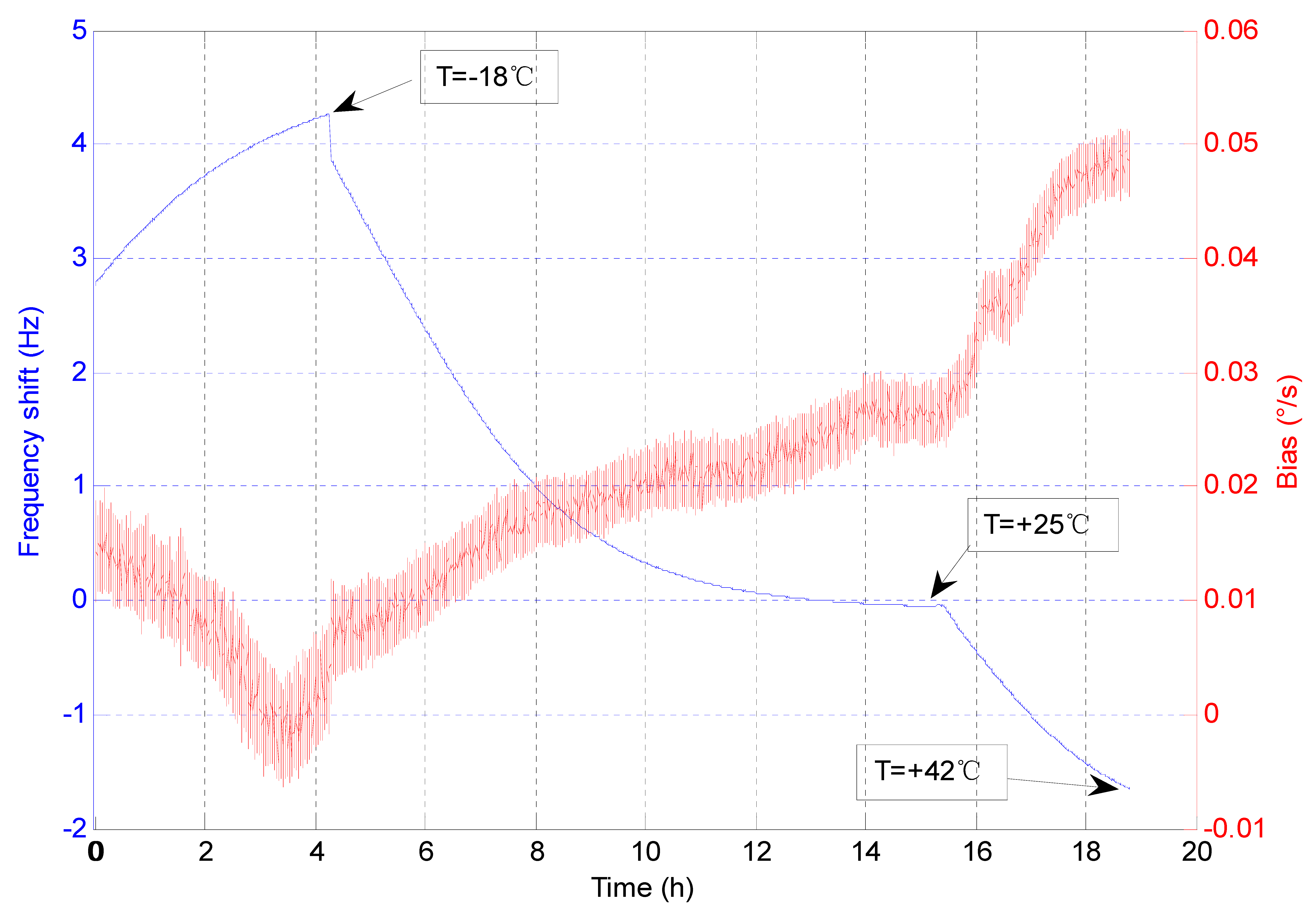
2.1. Temperature-Induced Bias Drift
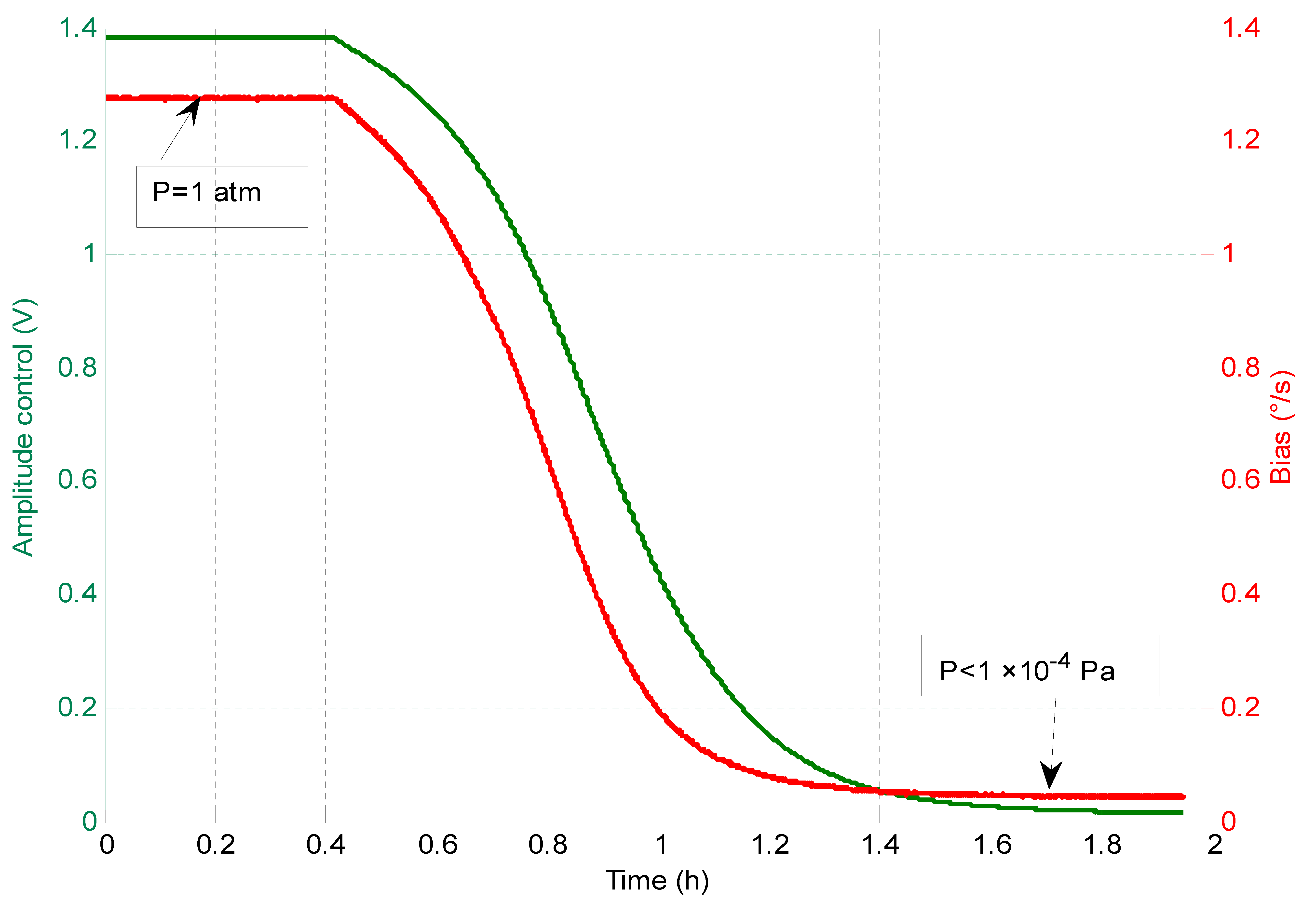
2.2. Air Pressure-Induced Bias Drift
2.3. Bias Compensation Using Drive-Mode Parameters
3. Results and Discussion
3.1. Comprehensive Effect Verification
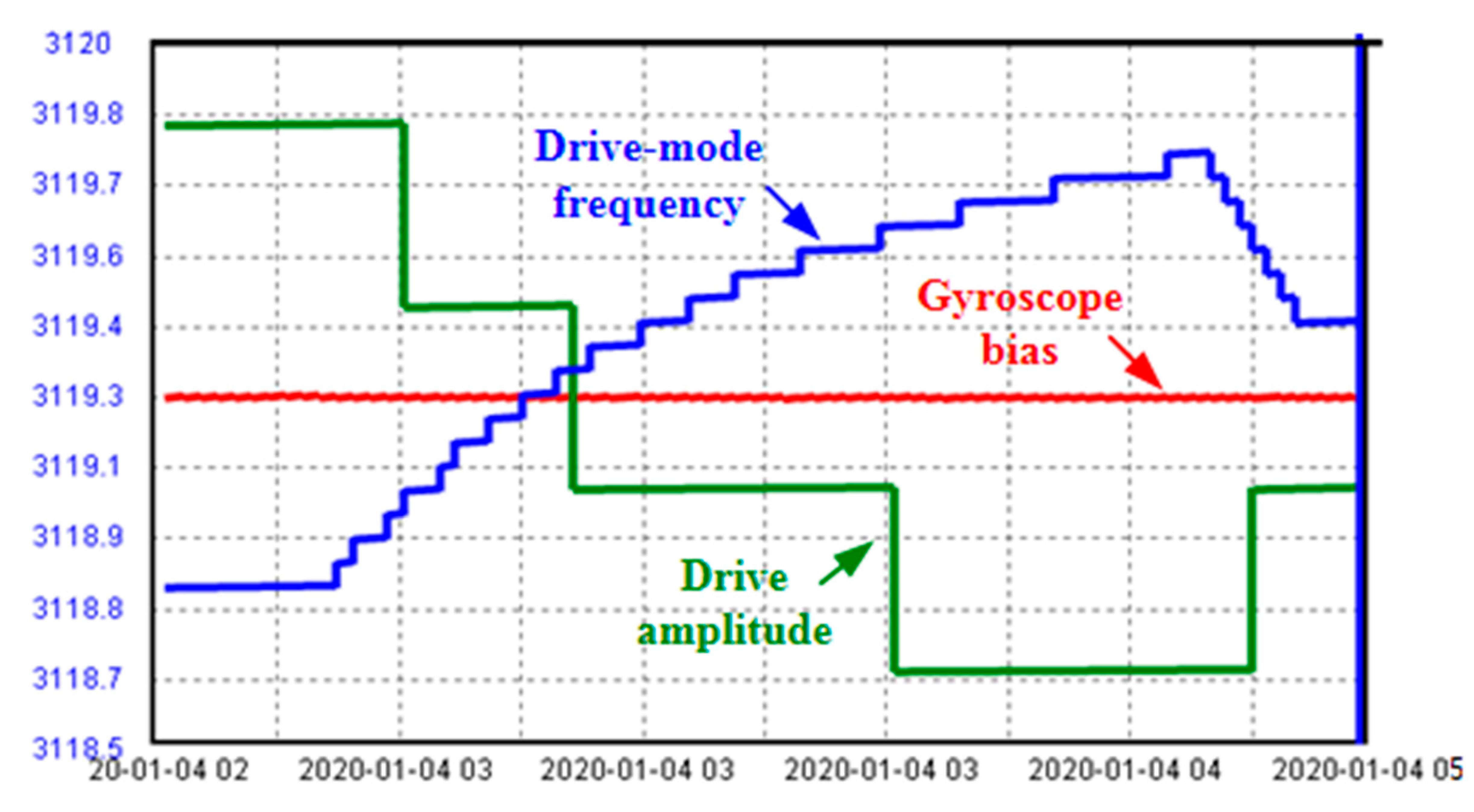
3.2. On-Orbit Experimental Demonstration
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, T.; Zhou, B.; Yin, P.; Chen, Z.; Zhang, R. Optimal Design of a Center Support Quadruple Mass Gyroscope (CSQMG). Sensors 2016, 16, 613. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wen, H.; Daruwalla, A.; Liu, C.-S.; Ayazi, F. A hermetically-sealed 2.9MHz N = 3 disk baw gyroscope with sub-degree-per-hour bias instability. In Proceedings of the 2020 IEEE 33rd International Conference on Micro Electro Mechanical Systems (MEMS), Vancouver, BC, Canada, 18–22 January 2020; pp. 741–744. [Google Scholar] [CrossRef]
- Dussy, S.; Durrant, D.; Moy, A.; Perriault, N.; Celerier, B. MEMS gyro for space applications overview of European activities. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005. [Google Scholar] [CrossRef]
- Syed, W.U.; An, B.H.; Mansouri, M.S.; Mohammed, Z.; Aldahmani, S.; Elfadel, I.M.; Choi, D.S. MEMS gyroscope for miniaturized space attitude control system. In Proceedings of the 2018 Symposium on Design, Test, Integration & Packaging of MEMS and MOEMS (DTIP), Roma, Italy, 22–25 May 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Guérard, J.; Larroque, M.; Lizin, G.; Verstraeten, L.; Delavoipière, G. MEMS gyroscope demonstration for space application using a DPC. In Proceedings of the AMICSA, Leuven, Belgium, 17–20 June 2018; pp. 15–21. [Google Scholar]
- Madni, A.; Costlow, L.; Knowles, S. Common design techniques for BEI GyroChip quartz rate sensors for both automotive and aerospace/defense markets. IEEE Sens. J. 2003, 3, 569–578. [Google Scholar] [CrossRef]
- Stanimirovic, I.; Stanimirovic, Z. MEMS Reliability. In Proceedings of the MIEL 2012, Nis, Serbia, 13–16 May 2012; pp. 173–175. [Google Scholar]
- Bandi, T.; Polido-Gomes, J.; Neels, A.; Dommann, A.; Shea, H. Making MEMS more suited for Space: Assessing the proton-radiation tolerance of structural materials for microsystems in orbit. In Reliability, Packaging, Testing, and Characterization of MOEMS/MEMS and Nanodevices XII; International Society for Optics and Photonics: Bellingham, WA, USA, 2013; Volume 8614, p. 86140M. [Google Scholar]
- Jandakl, M.; Vaqner, M.; Neuzil, T. Reduction of vibration and mechanical shocks in MEMS gyroscopes for space application. In Proceedings of the 2018 DGON Inertial Sensors and Systems (ISS), Braunschweig, Germany, 11–12 September 2018; pp. 1–14. [Google Scholar] [CrossRef]
- Challoner, A.D.; Ge, H.H.; Liu, J.Y. Boeing Disc Resonator Gyroscope. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014; pp. 504–514. [Google Scholar]
- Kubena, R.L.; Stratton, F.P.; Huang, L.X.; Joyce, R.J.; Kirby, D.J.; Chang, D.T.; Yong, Y.K. Co-integration of a quartz OCXO and Si MEMS inertial sensors for improved navigational accuracy. In Proceedings of the 2016 IEEE International Frequency Control Symposium (IFCS), New Orleans, LA, USA, 9–12 May 2016; pp. 1–6. [Google Scholar]
- Singh, S.S.; Nagourney, T.; Cho, J.Y.; Darvishian, A.; Najafi, K.; Shiari, B. Design and fabrication of high-Q birdbath resonator for MEMS gyroscopes. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018; pp. 15–19. [Google Scholar] [CrossRef]
- Xiao, D.; Li, W.; Hou, Z.; Lu, K.; Shi, Y.; Wu, Y.; Wu, X. Fused Silica Micro Shell Resonator With T-Shape Masses for Gyroscopic Application. J. Microelectr. Syst. 2017, 27, 47–58. [Google Scholar] [CrossRef]
- Koenig, S.; Rombach, S.; Gutmann, W.; Jaeckle, A.; Weber, C.; Ruf, M.; Grolle, D.; Rende, J. Towards a navigation grade Si-MEMS gyroscope. In Proceedings of the 2019 DGON Inertial Sensors and Systems (ISS), Braunschweig, Germany, 10–11 September 2019; pp. 1–18. [Google Scholar]
- Xia, D.; Chen, S.; Wang, S.; Li, H. Microgyroscope Temperature Effects and Compensation-Control Methods. Sensors 2009, 9, 8349–8376. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Su, Y.; Qiu, A.P.; Xia, G.M. Self-temperature compensation for high quality factor micro-machined gyroscope. Opt. Precis. Eng. 2013, 21, 2870–2876. [Google Scholar] [CrossRef]
- Rui, F.; Anping, Q.; Qin, S.; Yan, S. Temperature characteristic of natural frequency of double-mass silicon micro-mechanical gyroscope. J. Nanjing Univ. Sci. Technol. 2013, 37, 94–100. [Google Scholar]
- Qian, J.; Liu, C.; Zhang, D.C.; Zhao, Y.P. Residual stresses in micro-electro-mechanical systems. J. Mech. Strength 2001, 23, 393–401. [Google Scholar]
- Hopcroft, M.; Nix, W.D.; Kenny, T.W. What is the Young’s Modulus of Silicon? J. Microelectr. Syst. 2010, 19, 229–238. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Chen, D.; Wang, J. Regulating parameters of electromagnetic micromachined vibrating ring gyroscope by feedback control. Micro Nano Lett. 2012, 7, 1234–1236. [Google Scholar] [CrossRef]
- Putty, M.W. A Micro-Machined Vibrating Ring Gyroscope. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 1995. [Google Scholar]
- Kim, B.; Hopcroft, M.A.; Candler, R.N.; Jha, C.M.; Agarwal, M.; Melamud, R.; Chandorkar, S.A.; Yama, G.; Kenny, T.W. Temperature Dependence of Quality Factor in MEMS Resonators. J. Microelectromech. Syst. 2008, 17, 755–766. [Google Scholar] [CrossRef] [Green Version]
- Piyabongkarn, D.; Rajamani, R.; Greminger, M. The development of a MEMS gyroscope for absolute angle measurement. IEEE Trans. Control Syst. Technol. 2005, 13, 185–195. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Yazdanpanah, M.J. Robust adaptive passivity-based control of open-loop unstable affine non-linear systems subject to actuator saturation. IET Control Theory Appl. 2017, 11, 2731–2742. [Google Scholar] [CrossRef]
- Gu, H.; Su, W.; Zhao, B.; Zhou, H.; Liu, X. A Design Methodology of Digital Control System for MEMS Gyroscope Based on Multi-Objective Parameter Optimization. Micromachines 2020, 11, 75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prikhodko, I.P.; Trusov, A.A.; Shkel, A.M. Compensation of drifts in high-Q MEMS gyroscopes using temperature self-sensing. Sens. Actuators A Phys. 2013, 201, 517–524. [Google Scholar] [CrossRef] [Green Version]



| Temperature/°C | Drive-Mode Frequency/Hz |
|---|---|
| −20 | 3121.64 |
| −5 | 3120.09 |
| 10 | 3118.58 |
| 35 | 3116.13 |
| 50 | 3114.61 |
| Pressure/Pa | Drive Amplitude/V |
|---|---|
| 101,000 | 1.38 |
| 80,000 | 1.11 |
| 10,000 | 0.15 |
| 2000 | 0.043 |
| 0.0001 | 0.015 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Fu, M.; Meng, C.; Li, J.; Li, K.; Hu, J.; Chen, X. Consideration of Thermo-Vacuum Stability of a MEMS Gyroscope for Space Applications. Sensors 2020, 20, 7172. https://doi.org/10.3390/s20247172
Liu J, Fu M, Meng C, Li J, Li K, Hu J, Chen X. Consideration of Thermo-Vacuum Stability of a MEMS Gyroscope for Space Applications. Sensors. 2020; 20(24):7172. https://doi.org/10.3390/s20247172
Chicago/Turabian StyleLiu, Jili, Mingrui Fu, Chao Meng, Jianpeng Li, Kai Li, Jun Hu, and Xiaojuan Chen. 2020. "Consideration of Thermo-Vacuum Stability of a MEMS Gyroscope for Space Applications" Sensors 20, no. 24: 7172. https://doi.org/10.3390/s20247172




