Research on High-Resolution Miniaturized MEMS Accelerometer Interface ASIC
Abstract
1. Introduction
2. Materials and Methods
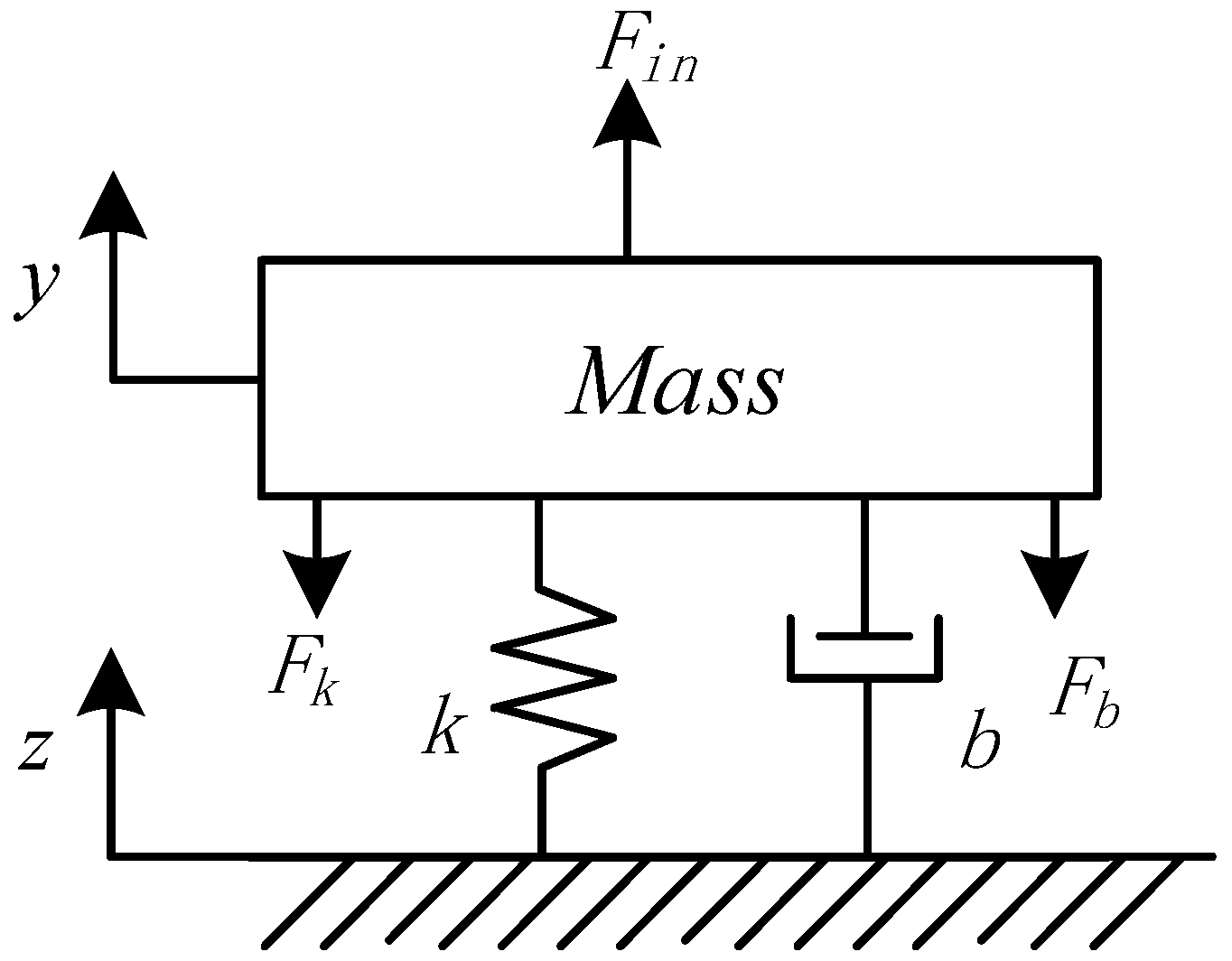
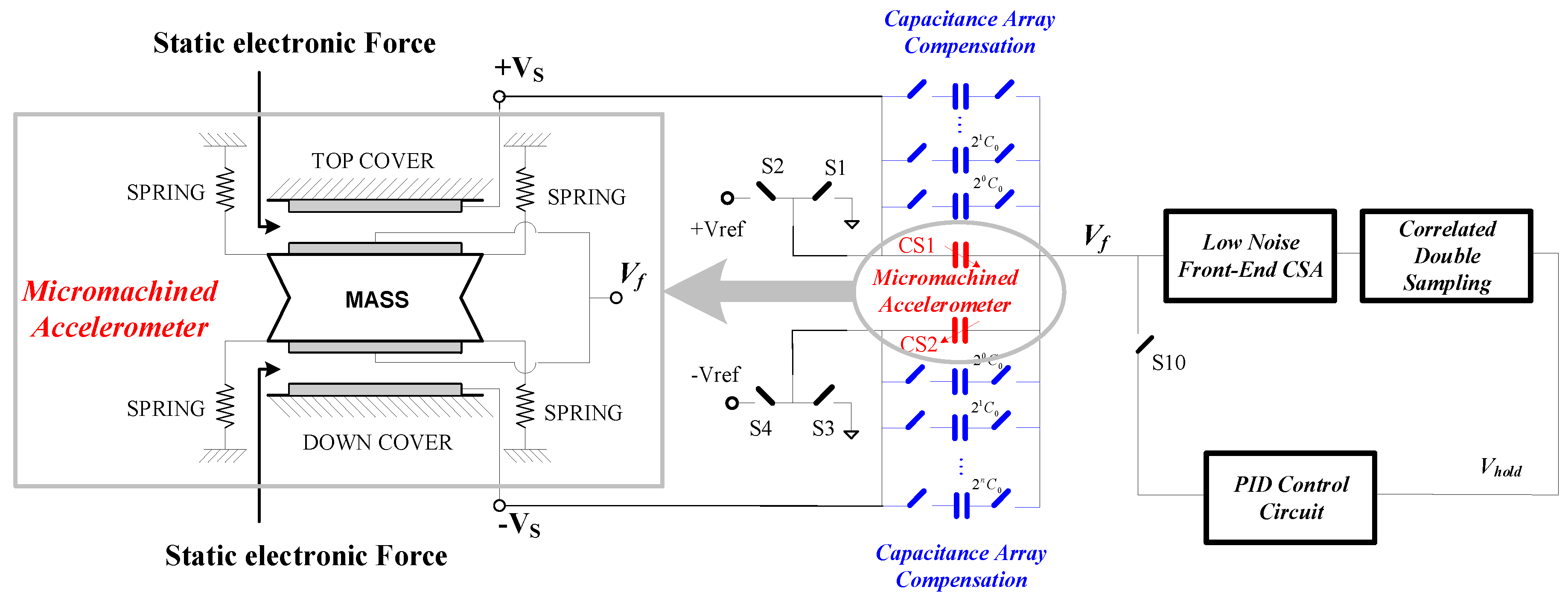
2.1. Accelerometer Sensitive Element and High-Resolution Closed-Loop Interface Circuit
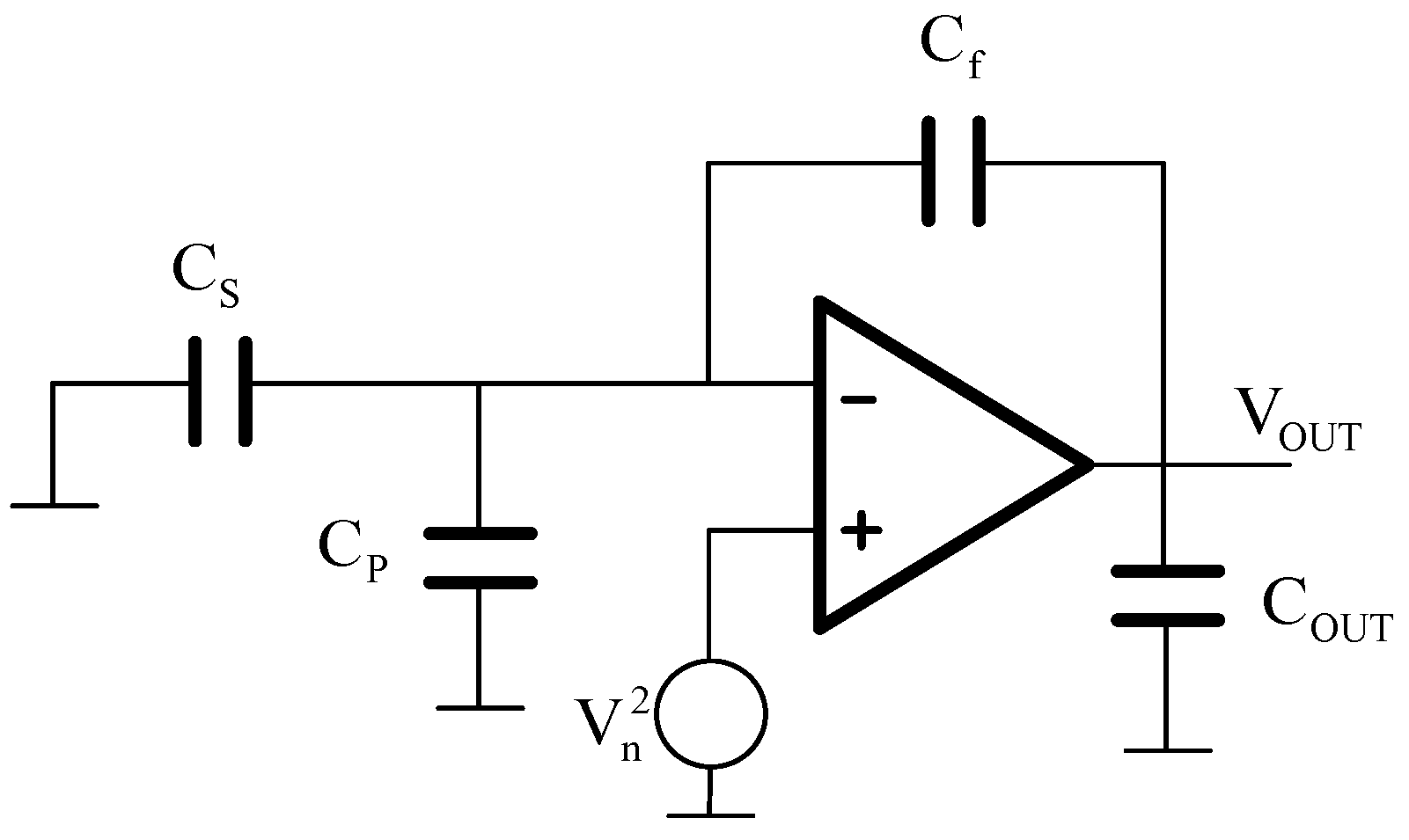
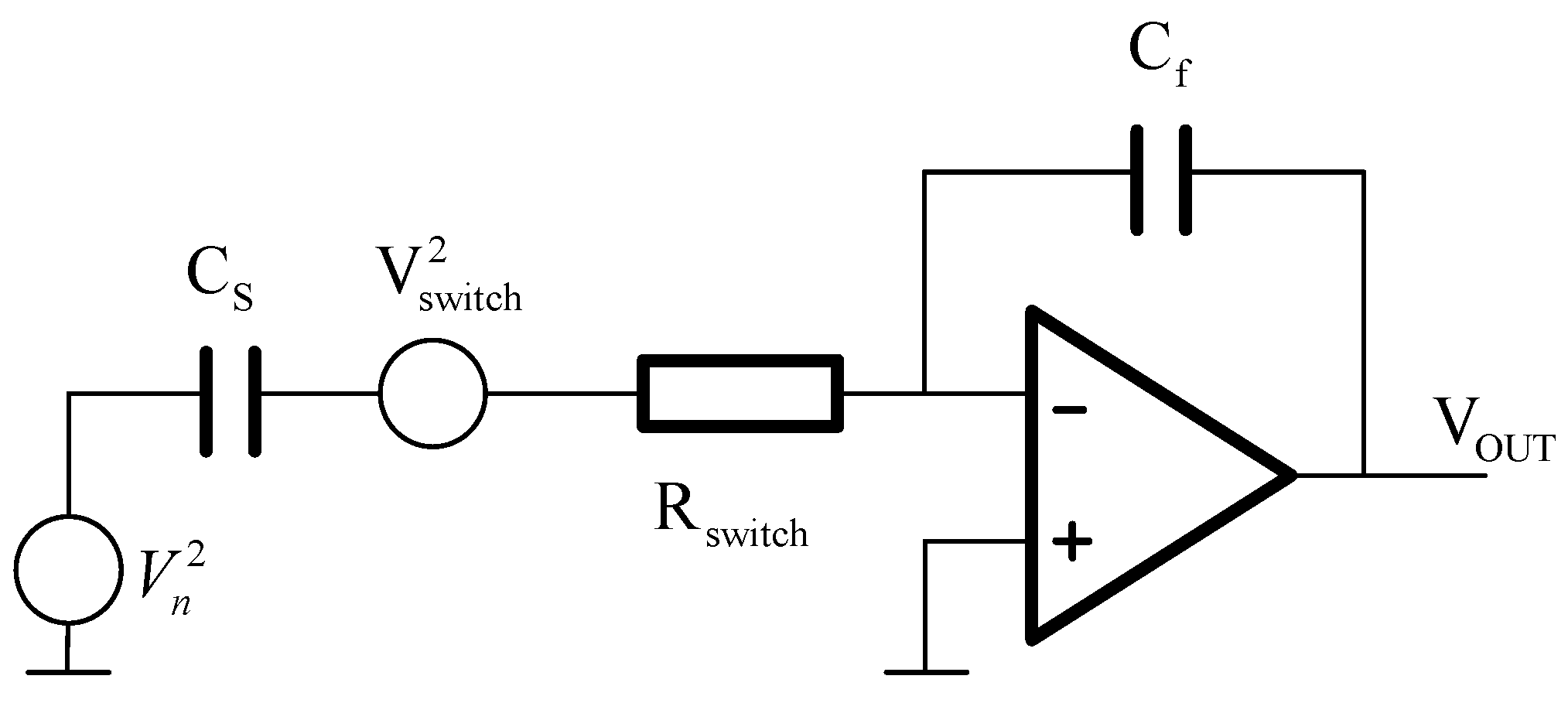
2.2. Noise Analysis of Closed-Loop Micromachined Accelerometers
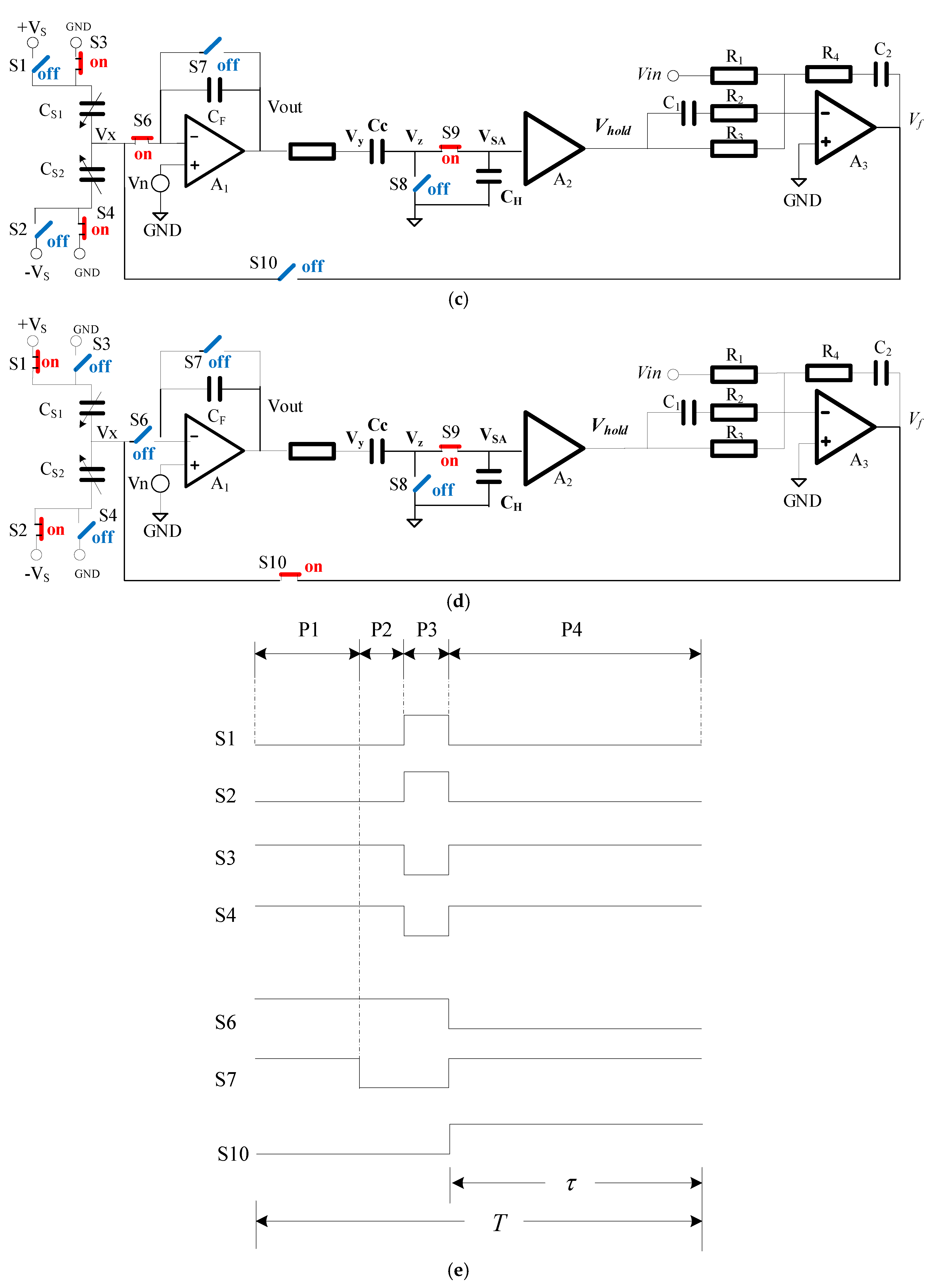
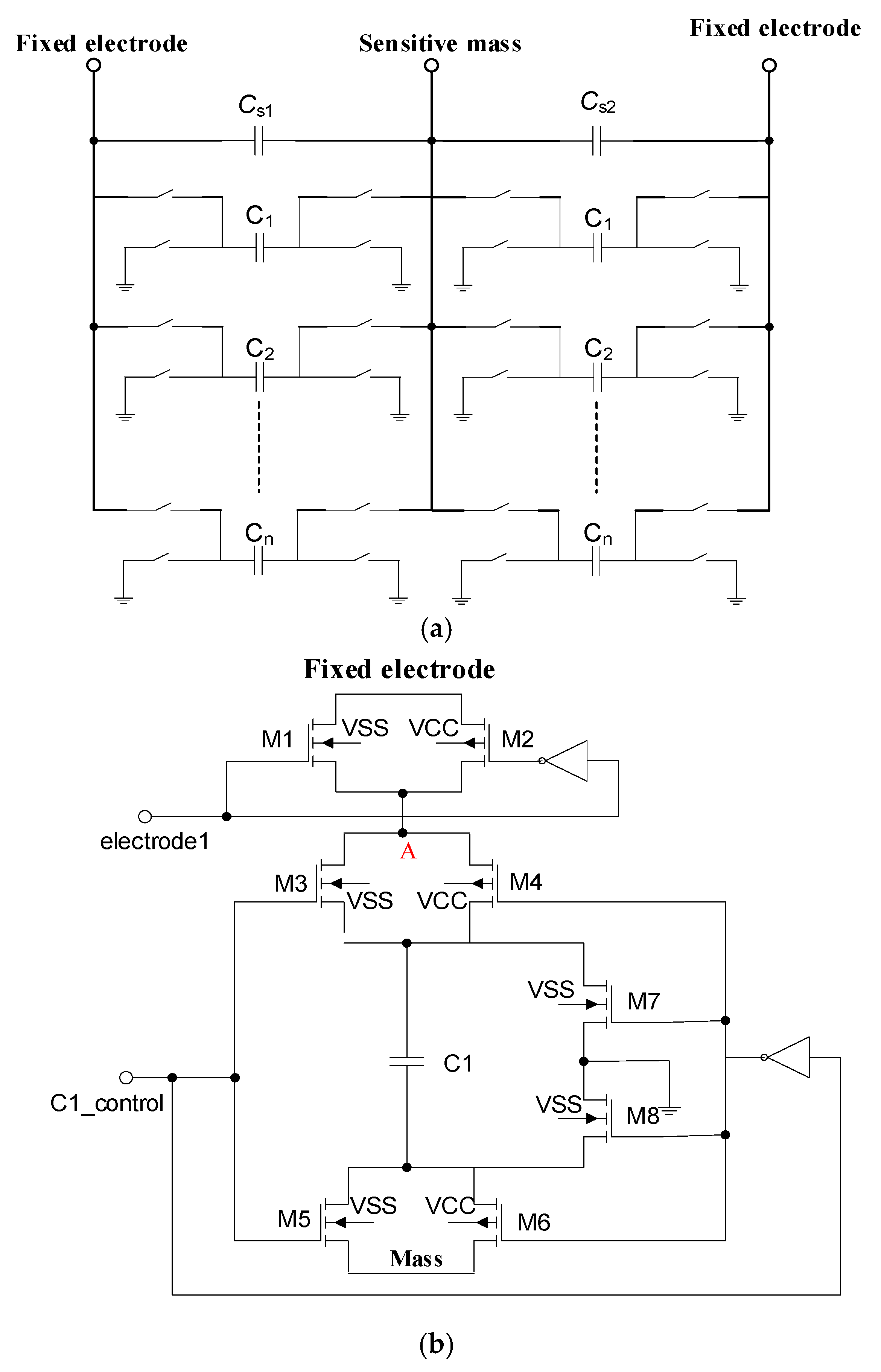
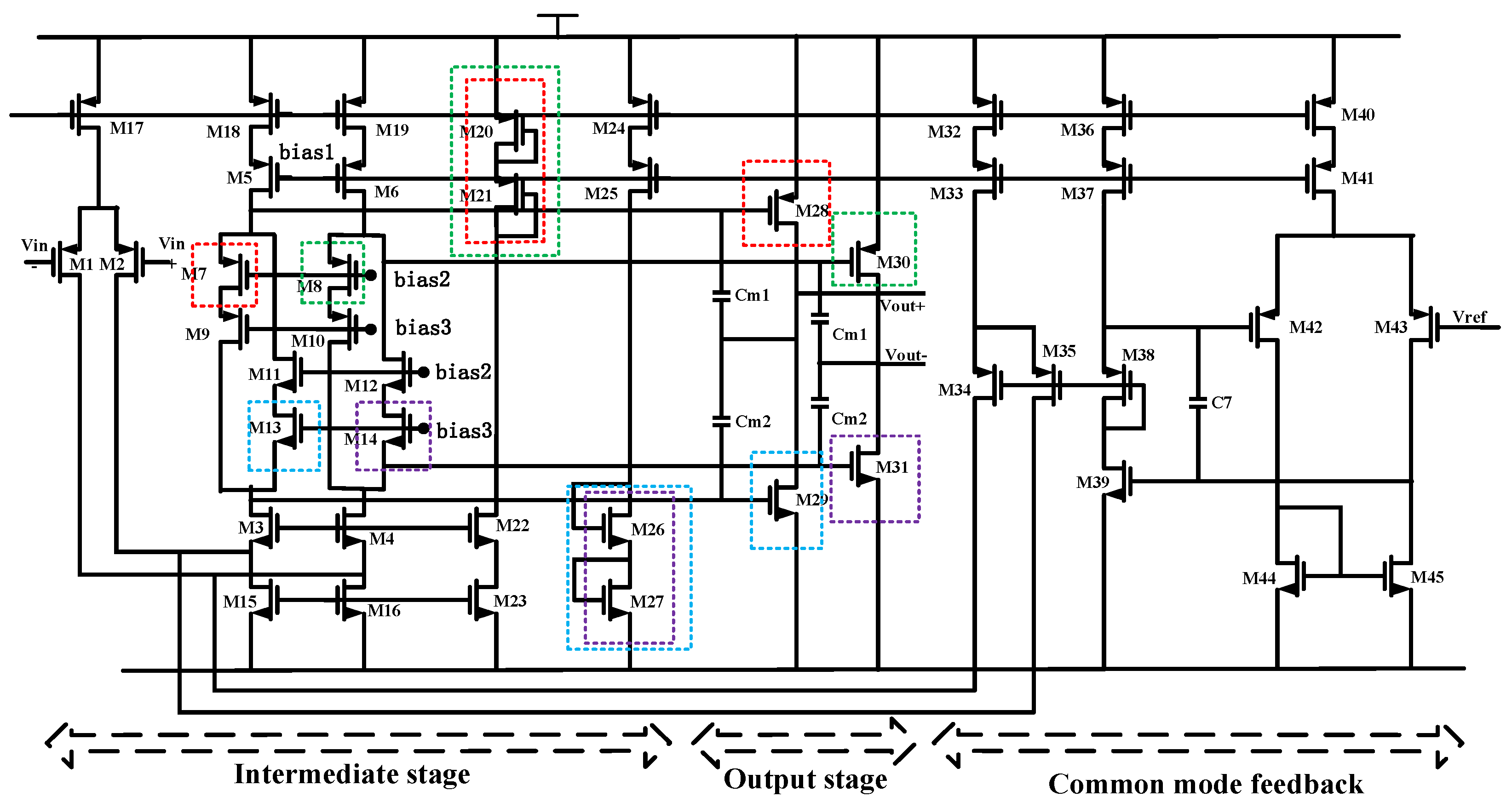
2.3. Interface Circuit Optimization and Design
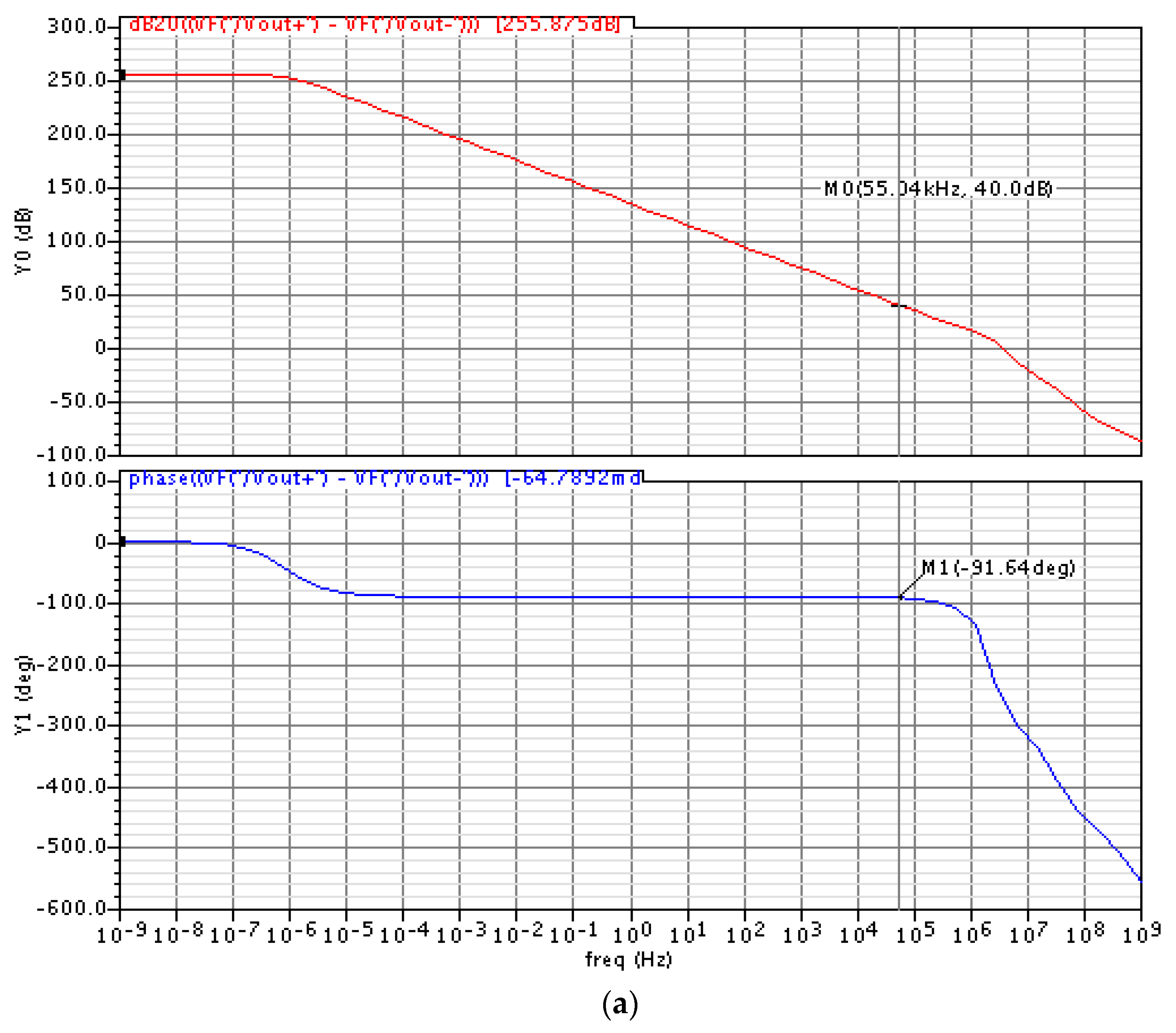
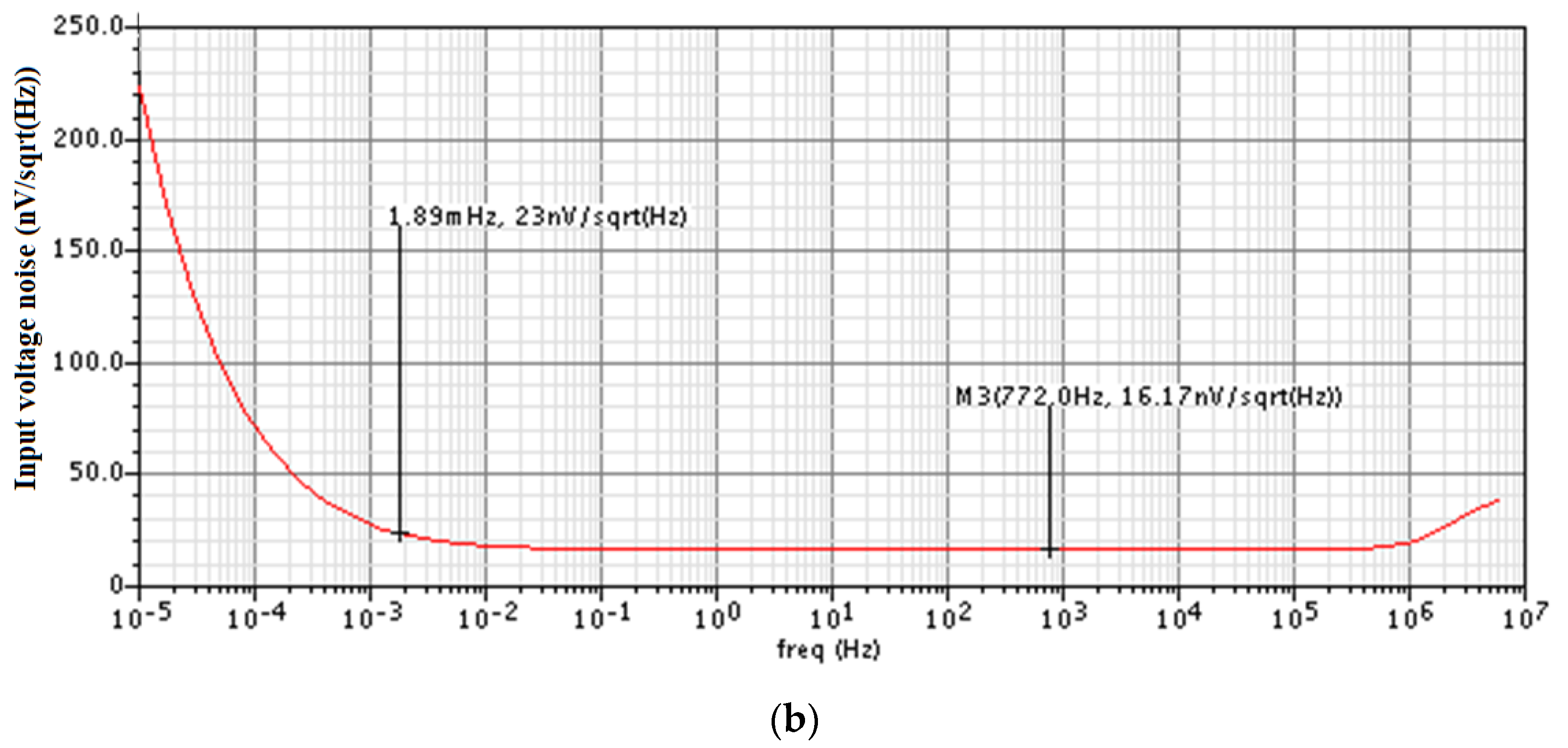
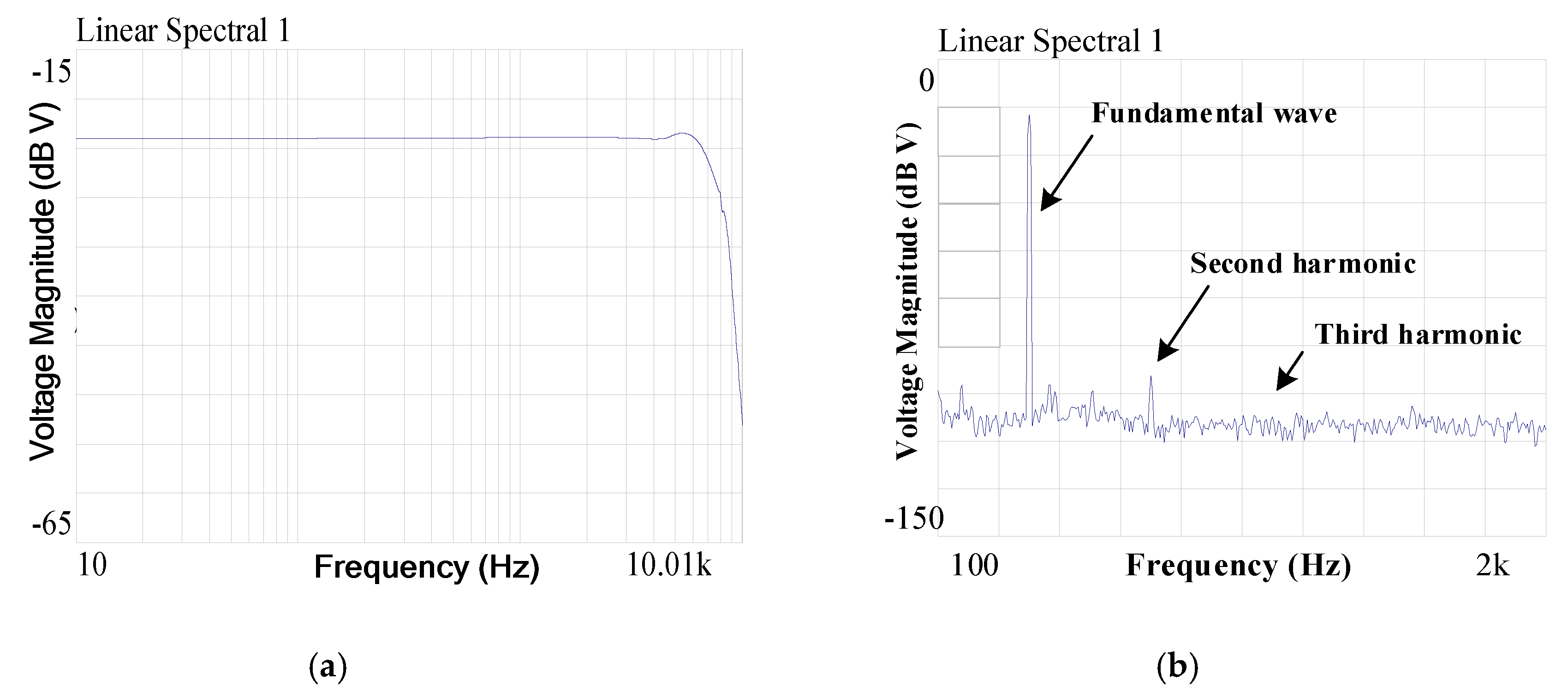
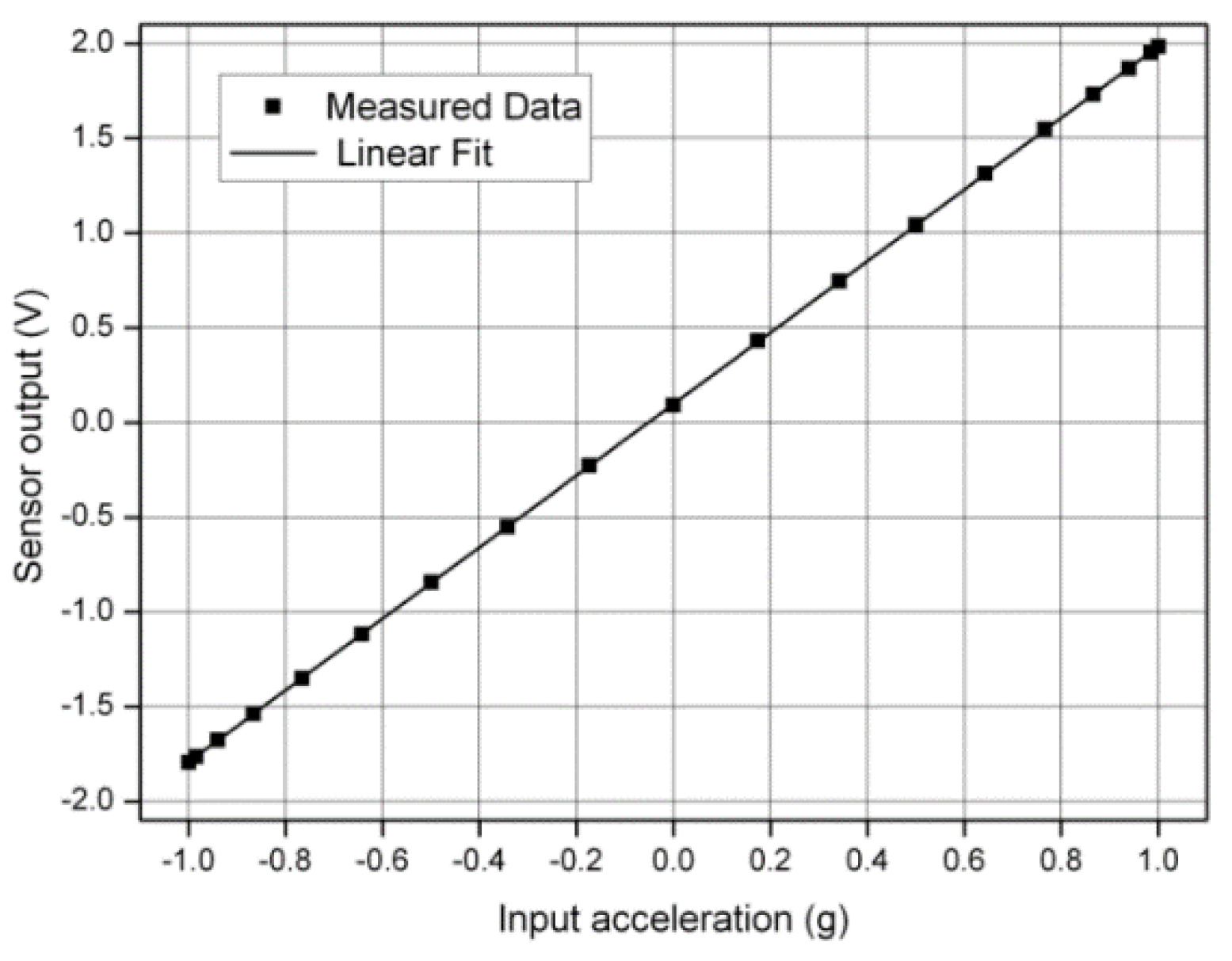
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, C.; Chen, F.; Wang, Y.; Sadeghpour, S.; Wang, C.X. Micromachined Accelerometers with Sub-mu g/root Hz Noise Floor: A Review. Sensors 2020, 20, 4054. [Google Scholar] [CrossRef]
- Yuan, Z.Y.; Han, E.C.; Meng, F.L.; Zuo, K.Y. Detection and Identification of Volatile Organic Compounds based on Temperature-Modulated ZnO Sensors. Instrum. Meas. IEEE Trans. 2020, 69, 4533–4544. [Google Scholar] [CrossRef]
- Soen, J.; Voda, A.; Condemine, C. Implementation of a CMOS/MEMS Accelerometer with ASIC Processes. Micromachines 2019, 10, 50. [Google Scholar]
- Chen, D.L.; Yin, L.; Fu, Q.; Zhang, W.B.; Wang, Y.H. A Straightforward Approach for Synthesizing Electromechanical Sigma-Delta MEMS Accelerometers. Sensors 2020, 20, 91. [Google Scholar] [CrossRef]
- Kar, S.K.; Chatterjee, P.; Mukherjee, B.; Swamy, K.B.M.M.; Sen, S. A Differential Output Interfacing ASIC for Integrated Capacitive Sensors. IEEE Trans. Instrum. Meas. 2018, 53, 196–203. [Google Scholar] [CrossRef]
- Li, X.Y.; Hu, J.P.; Liu, X.W. A High-Performance Digital Interface Circuit for a High-Q Micro-Electromechanical System Accelerometer. Micromachines 2018, 9, 675. [Google Scholar] [CrossRef]
- Gomez, J.M.; Bota, S.A.; Marco, S. Electrical equivalent modeling of MEMS differential capacitive accelerometer. Microelectron. J. 2020, 99, 104770. [Google Scholar]
- Petkov, V.P.; Balachandran, G.K.; Beintner, J. A Fully Differential Charge-Balanced Accelerometer for Electronic Stability Control. IEEE J. Solid-State Circuits 2014, 49, 262–270. [Google Scholar] [CrossRef]
- Li, H.W.; Zhai, Y.X.; Tao, Z.; Gui, Y.X.; Tan, X. Thermal Drift Investigation of an SOI-Based MEMS Capacitive Sensor with an Asymmetric Structure. Sensors 2020, 19, 3522. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.H.; Fu, Q.; Zhang, Y.F.; Liu, X.W. A Digital Closed-Loop Sense MEMS Disk Resonator Gyroscope Circuit Design Based on Integrated Analog Front-end. Sensors 2020, 20, 687. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.C.; Liu, B.D.; Yeh, C.Y. Design of a 0.6-V 0.2-mW CMOS MEMS Accelerometer. In Proceedings of the 2015 IEEE International Conference on Consumer Electronics, Taipei, Taiwan, 6–8 June 2015; pp. 444–445. [Google Scholar]
- Xu, H.L.; Liu, X.W.; Yin, L. A Closed-Loop Sigma Delta Interface for a High-Q Micromechanical Capacitive Accelerometer with 200 ng/root Hz Input Noise Density. IEEE J. Solid-State Circuits 2015, 50, 2101–2112. [Google Scholar] [CrossRef]
- Chen, D.L.; Liu, X.W.; Yin, L.; Wang, Y.H.; Shi, Z.H.; Zhang, G.R. A Sigma Delta Closed-Loop Interface for a MEMS Accelerometer with Digital Built-In Self-Test Function. Micromachines 2018, 9, 444. [Google Scholar] [CrossRef] [PubMed]
- Amini, B.V.; Abdolvand, R.; Ayazi, F. A 4.5-mW closed-loop micro-gravity CMOS SOI accelerometer. IEEE J. Solid-State Circuits 2006, 41, 2983–2991. [Google Scholar] [CrossRef]
- Aaltonen, L.; Rahikkala, P.; Saukoski, M.; Halonen, K. High-resolution continuous time interface for micromachined capacitive accelerometer. Int. J. Circuit Theory Appl. 2009, 37, 333–349. [Google Scholar] [CrossRef]
- Aaltonen, L.; Halonen, K. Continuous-time interface for a micromachined capacitive accelerometer with NEA of 4 g and bandwidth of 300 H. Sens. Actuators A Phys. 2009, 154, 46–56. [Google Scholar] [CrossRef]
- Chen, D.L.; Yin, L.; Fu, Q.; Liu, X.W. Measuring and calibrating of the parasitic mismatch in MEMS accelerometer based on harmonic distortion self-test. Sens. Actuators A Phys. 2020, 313, 112159. [Google Scholar] [CrossRef]
- Zhong, L.J.; Yang, J.; Xu, D.L.; Lai, X.Q. Bandwidth-Enhanced Oversampling Successive Approximation Readout Technique for Low-Noise Power-Efficient MEMS Capacitive Accelerometer. IEEE J. Solid-State Circuits 2020, 55, 2529–2538. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chan, P.K.; Li, H.K.H. A Low-Power Highly-Sensitive Capacitive Accelerometer IC Using Auto-Zero Time-Multiplexed Differential Technique. IEEE Sens. J. 2015, 15, 6179–6191. [Google Scholar] [CrossRef]
- Liu, D.D.; Liu, H.F.; Liu, J.Q. Gradient Method for Alleviating Bonding-Induced Warpage in a High-Precision Capacitive MEMS Accelerometer. Sensors 2020, 20, 1186. [Google Scholar] [CrossRef]
- Song, Z.; Sun, T.; Wu, J. System-Level Simulation and Implementation for a High Q Capacitive Accelerometer with PD Feedback Compensation. Microsyst. Technol. 2014, 21, 2233–2240. [Google Scholar] [CrossRef]
- Chen, F.; Zhao, Y.; Wang, J.C.; Zou, H.S.; Kraft, M.; Li, X.X. A Single-Side Fabricated Triaxis (111)-Silicon Microaccelerometer with Electromechanical Sigma–Delta Modulation. IEEE J. Solid-State Circuits 2018, 18, 1859–1869. [Google Scholar] [CrossRef]
- Akita, I.; Okazawa, T.; Kurui, Y.; Fujimoto, A.; Asano, T. A Feedforward Noise Reduction Technique in Capacitive MEMS Accelerometer Analog Front-End for Ultra-Low-Power IoT Applications. IEEE J. Solid-State Circuits 2020, 55, 1599–1609. [Google Scholar] [CrossRef]
- Yucetas, M.; Pulkkinen, M.; Kalanti, A. A high-resolution accelerometer with electrostatic damping and improved supply sensitivity. IEEE J. Sens. 2012, 47, 1721–1730. [Google Scholar] [CrossRef]
- Pastre, M.; Kayal, M.; Schmid, H.; Huber, A. A 300Hz 19b DR capacitive accelerometer based on a versatile front end in a 5th-order ΔΣ loop. In Proceedings of the 2009 Proceedings of ESSCIRC, Athens, Greece, 14–18 September 2009; pp. 288–291. [Google Scholar]




| Parameters | Value |
|---|---|
| Sensitivity | 200 ± 2 mV/g |
| Full-scale range | ±10 g |
| Bandwidth (−3 dB) | 0 to ≥2.4 kHz |
| Resonant frequency (ω0) | 2 kHz |
| Nonlinearity | <1% FS |
| Noise spectral density in band | 25 μV/ |
| The Noise Source | Theoretical Expression |
|---|---|
| Thermal noise of the sensitive element | |
| The equivalent noise of the pre-stage charge-sensitive amplifier (CSA) | |
| The equivalent noise of the reference voltage | |
| The equivalent noise of the switch |
| MEMS Sensitive Element and Interface Circuit | |
|---|---|
| Sensitivity (mV/g) | 1200 |
| Input range (g) | ±1.2 |
| Bandwidth (Hz) | 1000 |
| Power dissipation (mW) | 7.7 |
| Nonlinearity | 0.15% |
| Bias instability (μg) | 50 μg |
| Noise floor (μg/Hz1/2) | 0.5 (@200 Hz) |
| Parameters | [24] | [16] | [14] | [25] | This Work |
|---|---|---|---|---|---|
| Circuit structure | Hybrid S-C | Closed-loop continuous-time | Closed-loop S-C | Closed-loop S-C | Closed-loop S-C |
| Process (μm) | 0.35 | 0.7 | 0.5 | 0.6 | 0.35 |
| Sensitivity(V/g) | 0.495 | 2.267 | NA | 0.373 | 1.2 |
| Noise floor (μg/Hz1/2) | 2(@200 Hz) | 0.3 (@300 Hz) | 4 (@500 Hz) | 1.15 (@300 Hz) | 0.5 (@200 Hz) |
| Power (mW) | 3.6 | 85.8 | 4.5 | 12 | 7.7 |
| Supply/Range | 3.6 V/±1.15 g | 5 V/±1.5 g | 3 V/NA | 9 V/±11 g | 5 V/±1.2 g |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zheng, Y.; Kong, X.; Liu, Y.; Tang, D. Research on High-Resolution Miniaturized MEMS Accelerometer Interface ASIC. Sensors 2020, 20, 7280. https://doi.org/10.3390/s20247280
Li X, Zheng Y, Kong X, Liu Y, Tang D. Research on High-Resolution Miniaturized MEMS Accelerometer Interface ASIC. Sensors. 2020; 20(24):7280. https://doi.org/10.3390/s20247280
Chicago/Turabian StyleLi, Xiangyu, Yangong Zheng, Xiangyan Kong, Yupeng Liu, and Danling Tang. 2020. "Research on High-Resolution Miniaturized MEMS Accelerometer Interface ASIC" Sensors 20, no. 24: 7280. https://doi.org/10.3390/s20247280
APA StyleLi, X., Zheng, Y., Kong, X., Liu, Y., & Tang, D. (2020). Research on High-Resolution Miniaturized MEMS Accelerometer Interface ASIC. Sensors, 20(24), 7280. https://doi.org/10.3390/s20247280






