An Ensemble-Based Approach to Anomaly Detection in Marine Engine Sensor Streams for Efficient Condition Monitoring and Analysis
Abstract
:1. Introduction
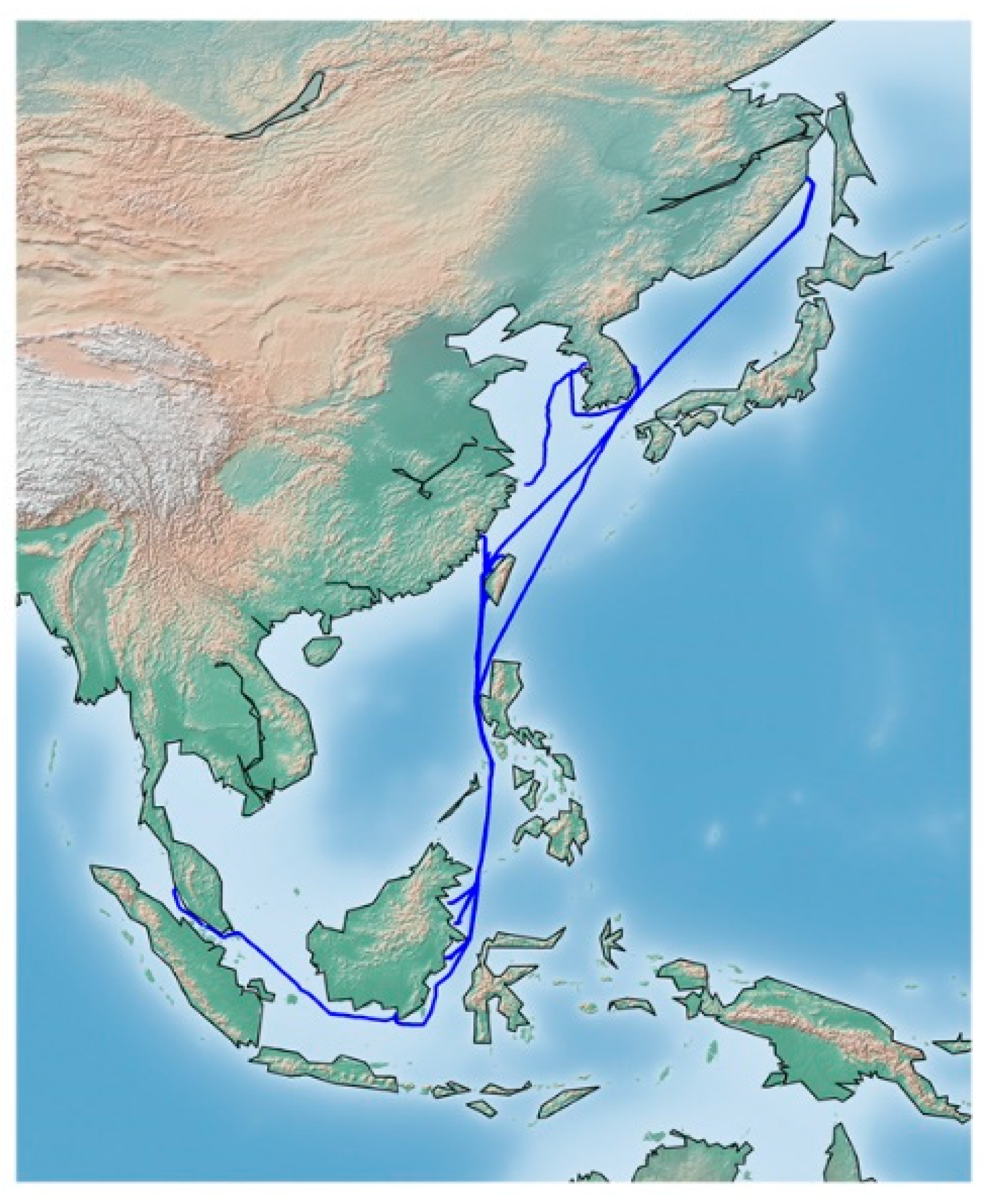
2. Data Description
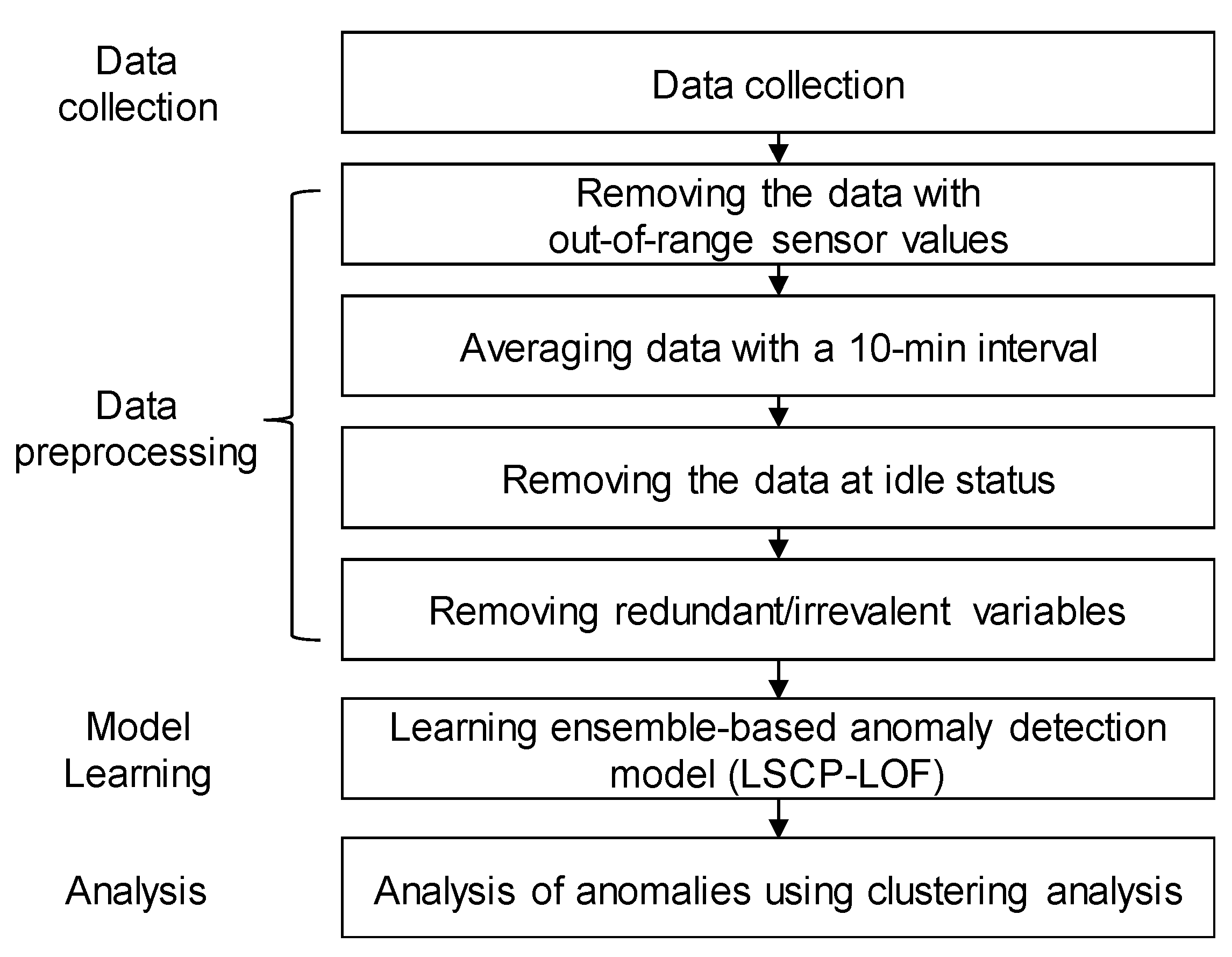
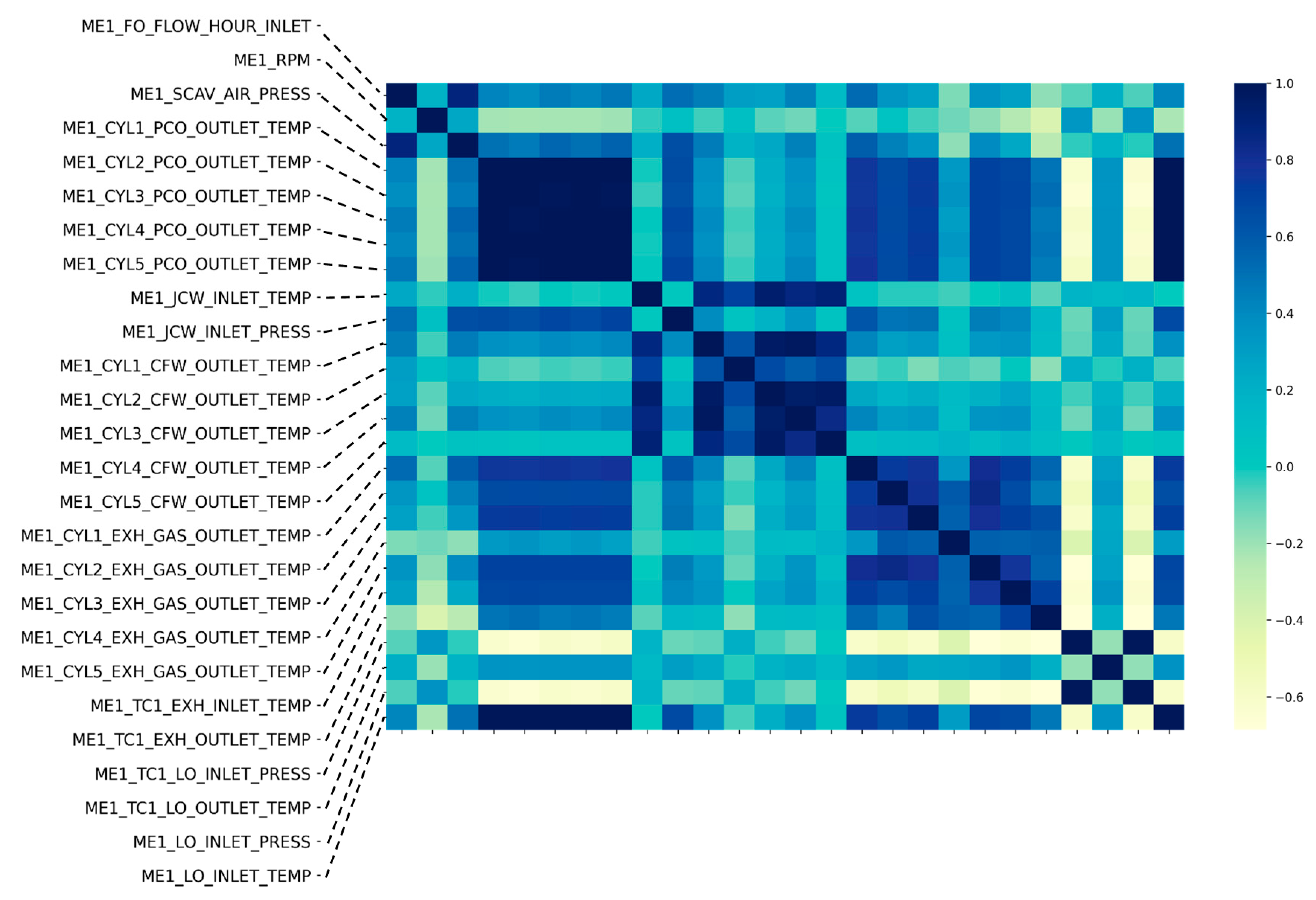
3. Data Preprocessing
4. Ensemble-Based Method for Anomaly Detection
4.1. Base Anomaly Detection Algorithm: Local Outlier Factor
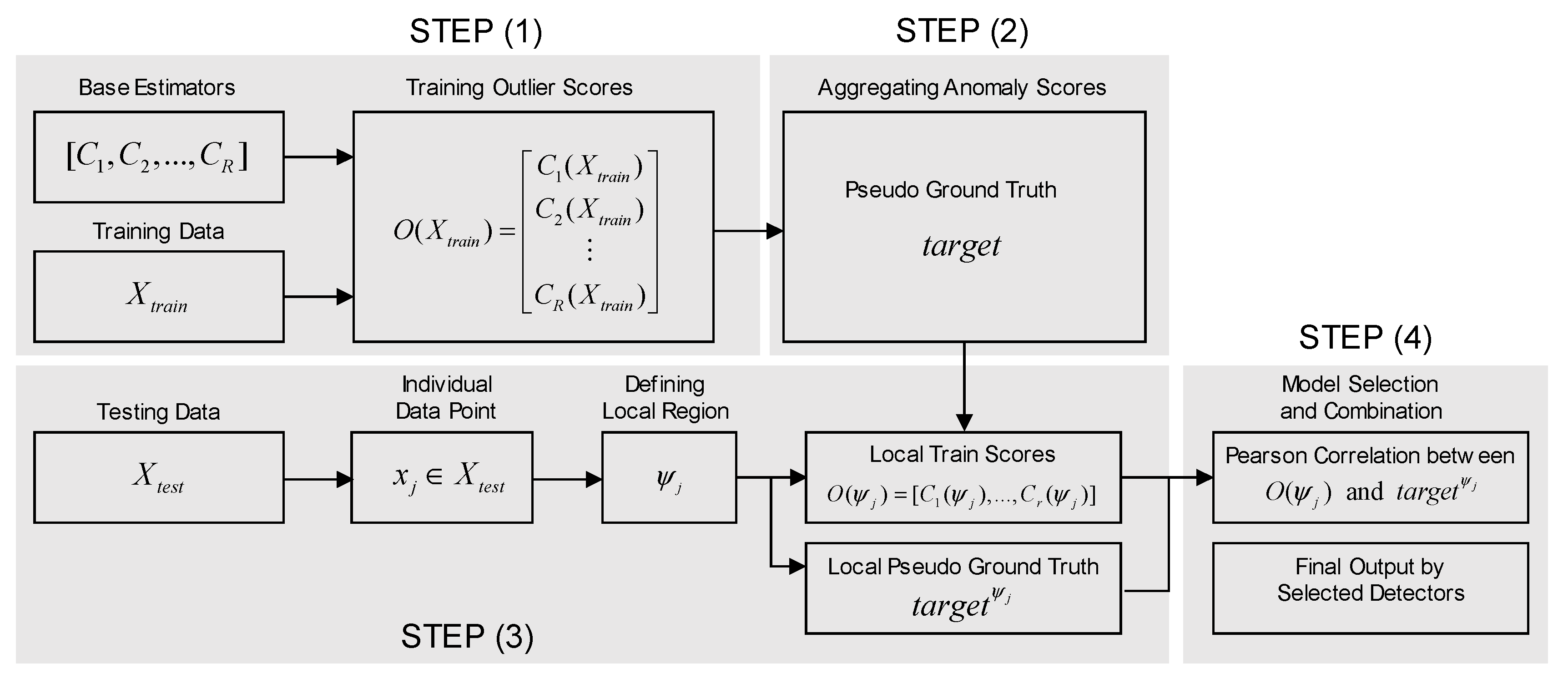
4.2. Ensemble-Based Approach to Anomaly Detection: LSCP
5. Experimental Result
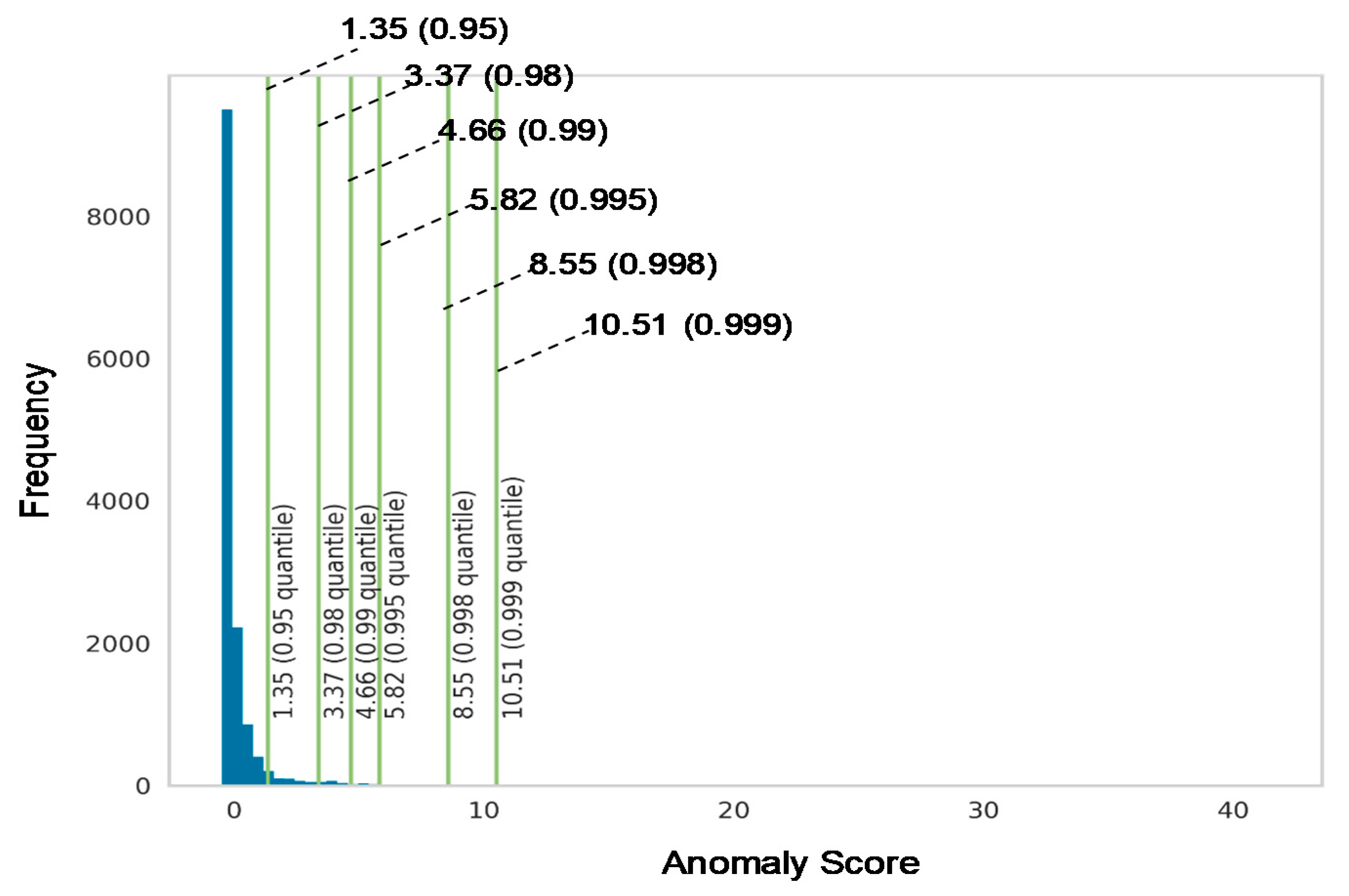
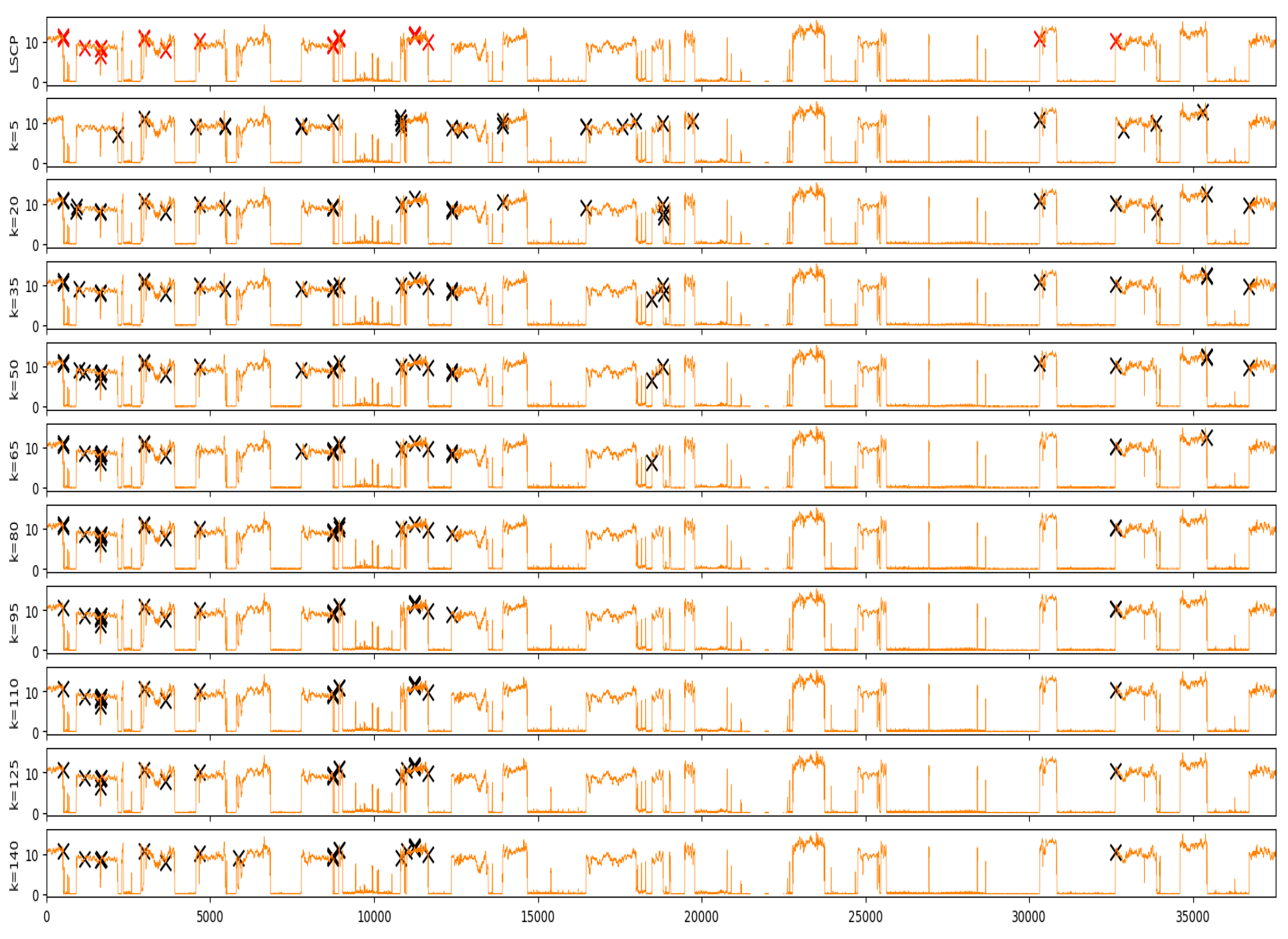
5.1. Anomalies Detection Result
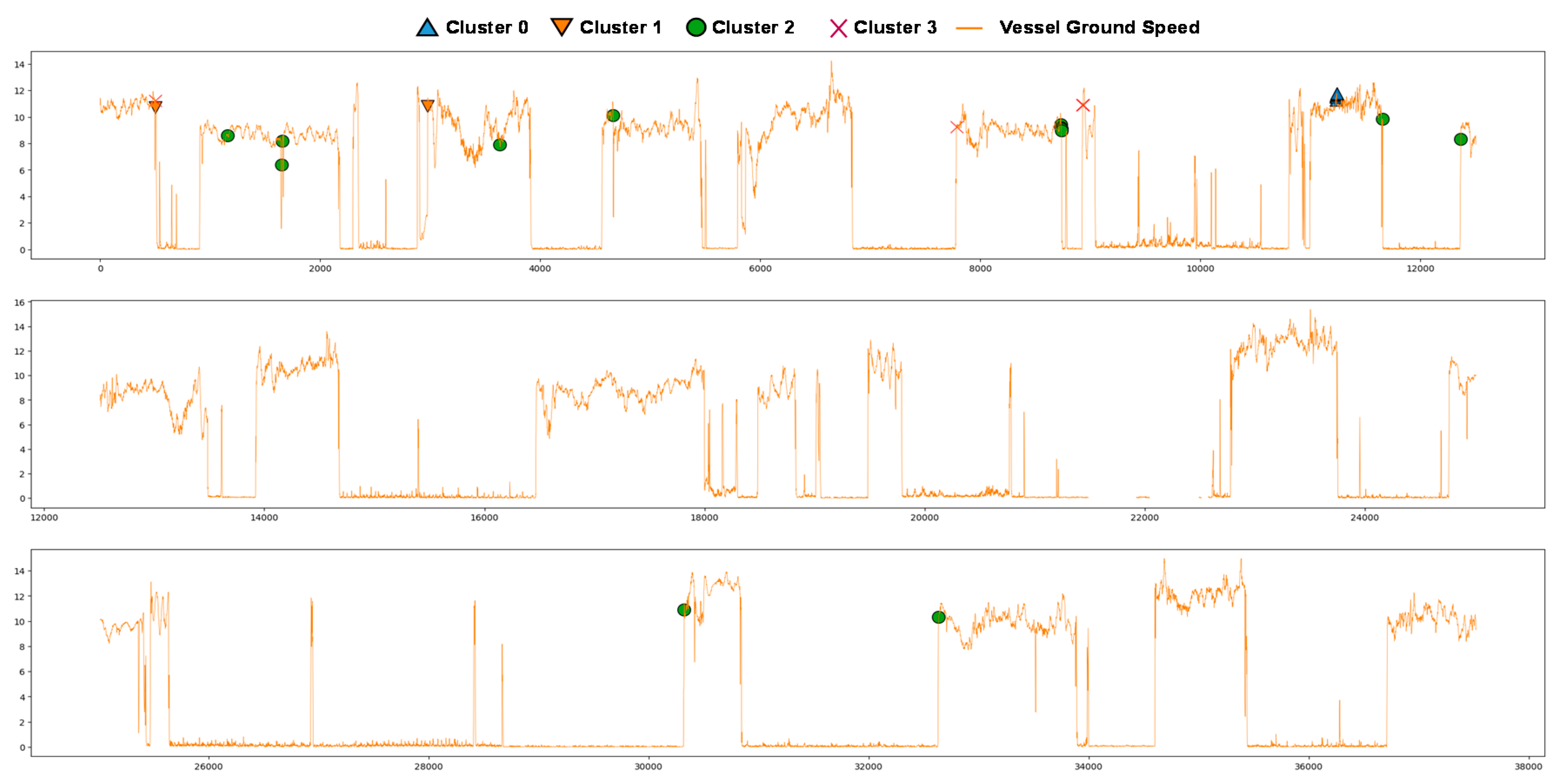
5.2. Anomalous Pattern Identification Using Clustering Analysis
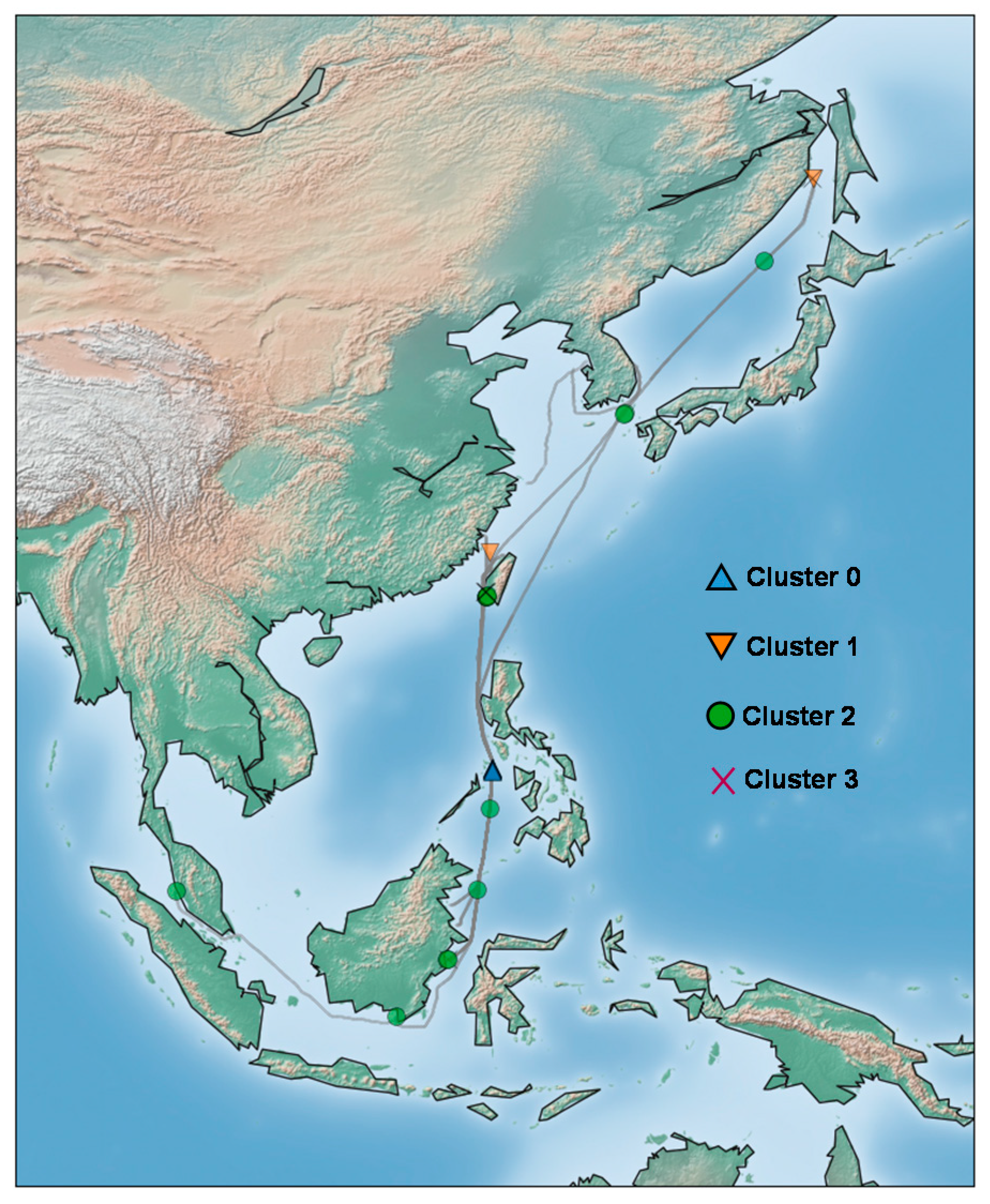
5.3. Anomalous Engine Status Analysis with Vessel Operational Information
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lazakis, I.; Turan, O.; Aksu, S. Increasing ship operational reliability through the implementation of a holistic maintenance management strategy. Ships Offshore Struct. 2010, 5, 337–357. [Google Scholar] [CrossRef]
- Jiang, R.; Yan, X. Condition Monitoring of Diesel Engines. In Complex System Maintenance Handbook; Springer: London, UK, 2008. [Google Scholar]
- Kandemir, C.; Celik, M. A human reliability assessment of marine auxiliary machinery maintenance operations under ship PMS and maintenance 4.0 concepts. Cogn. Technol. Work 2019, 22, 1–15. [Google Scholar] [CrossRef]
- Jimenez, V.J.; Bouhmala, N.; Gausdal, A.H. Developing a predictive maintenance model for vessel machinery. J. Ocean. Eng. Sci. 2019, 5, 358–386. [Google Scholar] [CrossRef]
- Perera, L.P.; Mo, B. Marine engine-centered data analytics for ship performance monitoring. J. Offshore Mech. Arct. Eng. 2017, 139, 021301. [Google Scholar] [CrossRef]
- Mak, L.; Sullivan, M.; Kuczora, A.; Millan, J. Ship performance monitoring and analysis to improve fuel efficiency. In Proceedings of the 2014 Oceans—St. John’s, St. John’s, NL, Canada, 14–19 September 2014. [Google Scholar]
- Aldous, L.; Smith, T.; Bucknall, R.; Thompson, P. Uncertainty analysis in ship performance monitoring. Ocean. Eng. 2015, 110, 29–38. [Google Scholar] [CrossRef]
- Soner, O.; Akyuz, E.; Celik, M. Use of tree-based methods in ship performance monitoring under operating conditions. Ocean. Eng. 2018, 166, 302–310. [Google Scholar] [CrossRef]
- Kim, D.; Lee, S.; Lee, J. Data-Driven Prediction of Vessel Propulsion Power Using Support Vector Regression with Onboard Measurement and Ocean Data. Sensors 2020, 20, 1588. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chi, H.; Pedrielli, G.; Ng, S.H.; Kister, T.; Bressan, S. A framework for real-time monitoring of energy efficiency of marine vessels. Energy 2018, 145, 246–260. [Google Scholar] [CrossRef]
- Gkerekos, C.; Lazakis, I.; Theotokatos, G. Machine learning models for predicting ship main engine Fuel Oil Consumption: A comparative study. Ocean. Eng. 2019, 188, 106282. [Google Scholar] [CrossRef]
- Strušnik, D.; Avsec, J. Artificial neural networking and fuzzy logic exergy controlling model of combined heat and power system in thermal power plant. Energy 2015, 80, 318–330. [Google Scholar] [CrossRef]
- Strušnik, D.; Marčič, M.; Golob, M.; Hribernik, A.; Živić, M.; Avsec, J. Energy efficiency analysis of steam ejector and electric vacuum pump for a turbine condenser air extraction system based on supervised machine learning modelling. Appl. Energy 2016, 173, 386–405. [Google Scholar] [CrossRef]
- Perera, L.P.; Mo, B. Data analysis on marine engine operating regions in relation to ship navigation. Ocean. Eng. 2016, 128, 163–172. [Google Scholar] [CrossRef]
- Perera, L.P.; Mo, B. Marine engine operating regions under principal component analysis to evaluate ship performance and navigation behavior. IFAC-Pap. 2016, 49, 512–517. [Google Scholar] [CrossRef]
- Brandsæter, A.; Vanem, E.; Glad, I.K. Efficient on-line anomaly detection for ship systems in operation. Expert Syst. Appl. 2019, 121, 418–437. [Google Scholar] [CrossRef]
- Vanem, E.; Brandsæter, A. Unsupervised anomaly detection based on clustering methods and sensor data on a marine diesel engine. J. Mar. Eng. Technol. 2019, 1–18. [Google Scholar] [CrossRef]
- Bae, Y.M.; Kim, M.J.; Kim, K.J.; Jun, C.H.; Byeon, S.S.; Park, K.M. A Case Study on the Establishment of Upper Control Limit to Detect Vessel’s Main Engine Failures using Multivariate Control Chart. J. Soc. Nav. Archit. Korea 2018, 55, 505–513. [Google Scholar] [CrossRef]
- Phaladiganon, P.; Kim, S.B.; Chen, V.C.; Baek, J.G.; Park, S.K. Bootstrap-based T 2 multivariate control charts. Commun. Stat. Simul. Comput. 2011, 40, 645–662. [Google Scholar] [CrossRef]
- Mason, R.L.; Young, J.C. Multivariate Statistical Process Control with Industrial Applications; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2002. [Google Scholar]
- MAN Two Stroke—Project Guide. Available online: https://marine.man-es.com/two-stroke/project-guides (accessed on 20 November 2020).
- Chu, C.S.J. Time series segmentation: A sliding window approach. Inf. Sci. 1995, 85, 147–173. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 1995, 41, 1–58. [Google Scholar] [CrossRef]
- Das, S.; Wong, W.K.; Dietterich, T.; Fern, A.; Emmott, A. Incorporating expert feedback into active anomaly discovery. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining, Barcelona, Spain, 12–15 December 2016. [Google Scholar]
- Aggarwal, C.C. Outlier ensembles: Position paper. ACM Sigkdd Explor. Newsl. 2013, 14, 49–58. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 16–18 May 2000. [Google Scholar]
- Ramaswamy, S.; Rastogi, R.; Shim, K. Efficient algorithms for mining outliers from large data sets. ACM Sigmod Rec. 2000, 29, 427–438. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Outlier Analysis; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Zhao, Y.; Nasrullah, Z.; Hryniewicki, M.K.; Li, Z. LSCP: Locally selective combination in parallel outlier ensembles. In Proceedings of the 2019 SIAM International Conference on Data Mining, Calgary, AB, Canada, 2–4 May 2019. [Google Scholar]
- Zhao, Y.; Nasrullah, Z.; Li, Z. PyOD: A Python Toolbox for Scalable Outlier Detection. J. Mach. Learn. Res. 2019, 20, 1–7. [Google Scholar]
- Huang, Y.; Hong, G. Investigation of the effect of heated ethanol fuel on combustion and emissions of an ethanol direct injection plus gasoline port injection (EDI + GPI) engine. Energy Convers. Manag. 2019, 123, 338–347. [Google Scholar] [CrossRef]
- Rubio, J.A.P.; Vera-García, F.; Grau, J.H.; Cámara, J.M.; Hernandez, D.A. Marine diesel engine failure simulator based on thermodynamic model. Appl. Therm. Eng. 2018, 144, 982–995. [Google Scholar] [CrossRef]
- Cicek, K.; Turan, H.H.; Topcu, Y.I.; Searslan, M.N. Risk-based preventive maintenance planning using Failure Mode and Effect Analysis (FMEA) for marine engine systems. In Proceedings of the 2010 Second International Conference on Engineering System Management and Applications, Sharjah, UAE, 30 March–1 April 2010. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should I trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]



| Specification | |
|---|---|
| Length Overall Length between perpendiculars Breadth Depth Draught Deadweight | 269.36 m 259.00 m 43.00 m 23.80 m 17.3 m 152.517 metric t |
| Sensor Name | Description |
|---|---|
| ME1 FO FLOW HOUR INLET | The consumption rate of fuel oil |
| ME1 FO TOTALIZER INLET | Cumulative consumption of fuel oil |
| ME1 FO TEMP INLET | The temperature of fuel oil |
| ME1 FO DENSITY INLET | The density of fuel oil |
| ME1 RPM ECC | Engine rotation per minute (RPM) |
| ME1 RPM | Same as above |
| ME1 SCAV AIR PRESS ECC | The Pressure of scavenging air |
| ME1 SCAV AIR PREE | Same as above |
| ME1 FO INLET TEMP | The inlet temperature of fuel oil |
| ME1 FO INLET PRESS | Inlet pressure of fuel oil |
| ME1 CYL1 PCO OUTLET TEMP ME1 CYL2 PCO OUTLET TEMP ME1 CYL3 PCO OUTLET TEMP ME1 CYL4 PCO OUTLET TEMP ME1 CYL5 PCO OUTLET TEMP | The outlet temperature of cylinder piston cooling oil |
| ME1 JCW INLET TEMP | The inlet temperature of jacket cooling water |
| ME1 JCW INLET OUTLET | The outlet temperature of jacket cooling water |
| ME1 CYL1 CFW OUT TEMP ME1 CYL2 CFW OUT TEMP ME1 CYL3 CFW OUT TEMP ME1 CYL4 CFW OUT TEMP ME1 CYL5 CFW OUT TEMP | The outlet temperature of cylinder block cooling water |
| ME1 CYL1 EXH GAS OUTLET TEMP ME1 CYL2 EXH GAS OUTLET TEMP ME1 CYL3 EXH GAS OUTLET TEMP ME1 CYL4 EXH GAS OUTLET TEMP ME1 CYL5 EXH GAS OUTLET TEMP | The outlet temperature of exhaust gas |
| ME1 TC1 EXH INLET TEMP | The inlet temperature of exhaust gas of turbocharger |
| ME1 TC1 EXH OUTLET TEMP | The outlet temperature of exhaust gas of turbocharger |
| ME1 TC LO OUTLET TEMP | The outlet temperature of lubricant oil |
| ME1 LO INLET PRESS | Inlet pressure of lubricant oil |
| ME1 LO INLET TEMP | The inlet temperature of lubricant oil |
| Reason | Parameters |
|---|---|
| Fuel Oil Status Indicator (not affect engine condition) | ME1 FO FLOW HOUR INLET, ME1 FO DENSITY INLET, ME1 FO TEMP INLET, ME1 FO TOTALIZER INLE |
| Duplicated sensors | ME1 RPM ECC, ME1 SCAV AIR PREES ECC |
| Aggregate value by averaging | ME1 [CYL1~CYL5] PCO OUTLET TEMP ME1 [CYL1~CYL5] PCO OUTLET TEMP ME1 [CYL1~CYL5] CFW OUTLET TEMP |
| Original Dataset | Preprocessed Dataset | |
|---|---|---|
| Parameters | ME1 FO FLOW HOUR INLET ME1 FO TOTALIZER INLET ME1 FO TEMP INLET ME1 FO DENSITY INLET ME1 RPM ECC ME1 RPM ME1 SCAV AIR PRESS ECC ME1 SCAV AIR PRESS ME1 FO INLET TEMP ME1 FO INLET PRESS ME1 [CYL1~CYL5] PCO OUTLET TEMP ME1 JCW INLET TEMP ME1 JCW INLET OUTLET ME1 [CYL1~CYL5] CFW OUT TEMP ME1 [CYL1~CYL5] EXH GAS OUTLET TEMP ME1 TC1 EXH INLET TEMP ME1 TC1 EXH OUTLET TEMP ME1 TC LO OUTLET TEMP ME1 LO INLET PRESS ME1 LO INLET TEMP | ME1 RPM ME1 SCAV AIR PRESS ME1 FO INLET TEMP ME1 FO INLET PRESS ME1 CYL PCO OUTLET TEMP (Average value of 5 cylinders) ME1 JCW INLET TEMP ME1 JCW INLET OUTLET ME1 CYL CFW OUT TEMP (Average value of 5 cylinders) ME1 CYL EXH GAS OUTLET TEMP (Average value of 5 cylinders) ME1 TC1 EXH INLET TEMP ME1 TC1 EXH OUTLET TEMP ME1 TC LO OUTLET TEMP ME1 TC LO INLET TEMP ME1 TC LO INLET PRESS |
| Number of Observations | 22,513,800 (one second interval) | 37,523 (ten minutes averaging) |
| Clusters | Anomalous Features |
|---|---|
| Cluster 0 | High fuel oil flow rate High engine RPM High scavenging air pressure High turbocharger lubricant oil outlet temperature |
| Cluster 1 | Low jacket cooling water inlet temperature Low turbocharger exhaust gas inlet temperature High turbocharger lubricant oil inlet pressure High lubricant oil inlet temperature Low cylinder block cooling water temperature Low cylinder exhaust gas outlet temperature |
| Cluster 3 | High scavenging air pressure Low turbocharger exhaust gas inlet temperature |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.; Lee, S.; Lee, J. An Ensemble-Based Approach to Anomaly Detection in Marine Engine Sensor Streams for Efficient Condition Monitoring and Analysis. Sensors 2020, 20, 7285. https://doi.org/10.3390/s20247285
Kim D, Lee S, Lee J. An Ensemble-Based Approach to Anomaly Detection in Marine Engine Sensor Streams for Efficient Condition Monitoring and Analysis. Sensors. 2020; 20(24):7285. https://doi.org/10.3390/s20247285
Chicago/Turabian StyleKim, Donghyun, Sangbong Lee, and Jihwan Lee. 2020. "An Ensemble-Based Approach to Anomaly Detection in Marine Engine Sensor Streams for Efficient Condition Monitoring and Analysis" Sensors 20, no. 24: 7285. https://doi.org/10.3390/s20247285
APA StyleKim, D., Lee, S., & Lee, J. (2020). An Ensemble-Based Approach to Anomaly Detection in Marine Engine Sensor Streams for Efficient Condition Monitoring and Analysis. Sensors, 20(24), 7285. https://doi.org/10.3390/s20247285





