A General Grid-Less Design Method for Location and Pressure Sensors with High Precision
Abstract
:1. Introduction
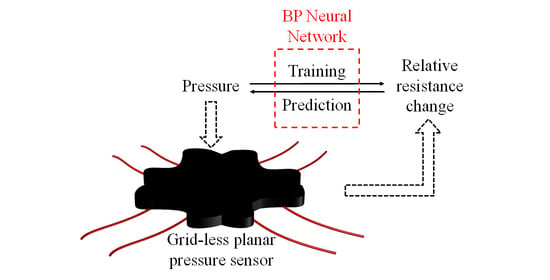
2. Pressure Sensor Fabrication and Measurement
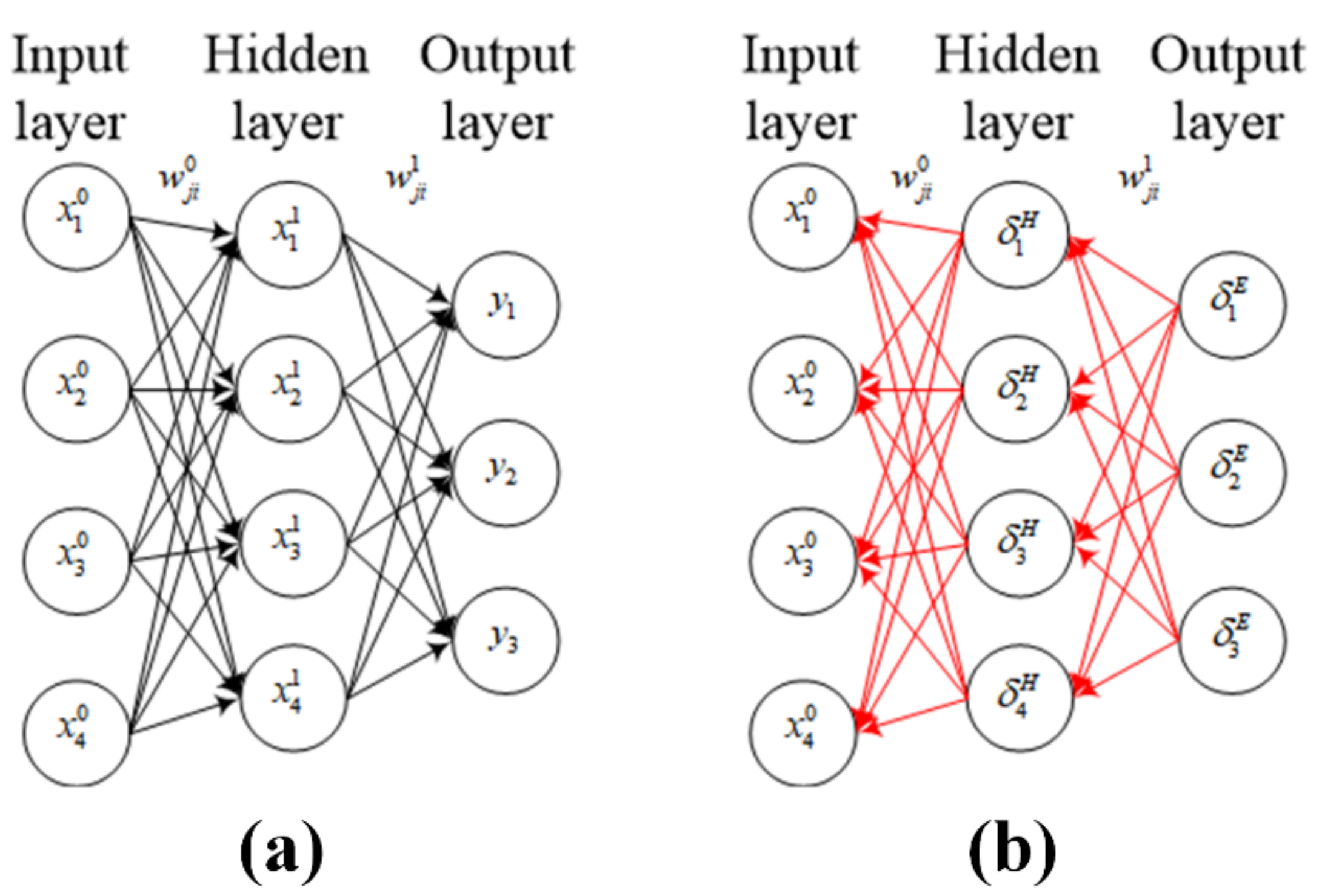
3. The BP Neural Network
4. Results and Discussions
4.1. Experimental Results and Analysis
4.2. Analysis of the Neural Network Prediction Performance
4.2.1. Precision Analysis
4.2.2. Accuracy Analysis
4.2.3. Repeatability Error Analysis
4.2.4. Training Sample Space Analysis
4.2.5. Analysis of the Impact of Material Uniformity
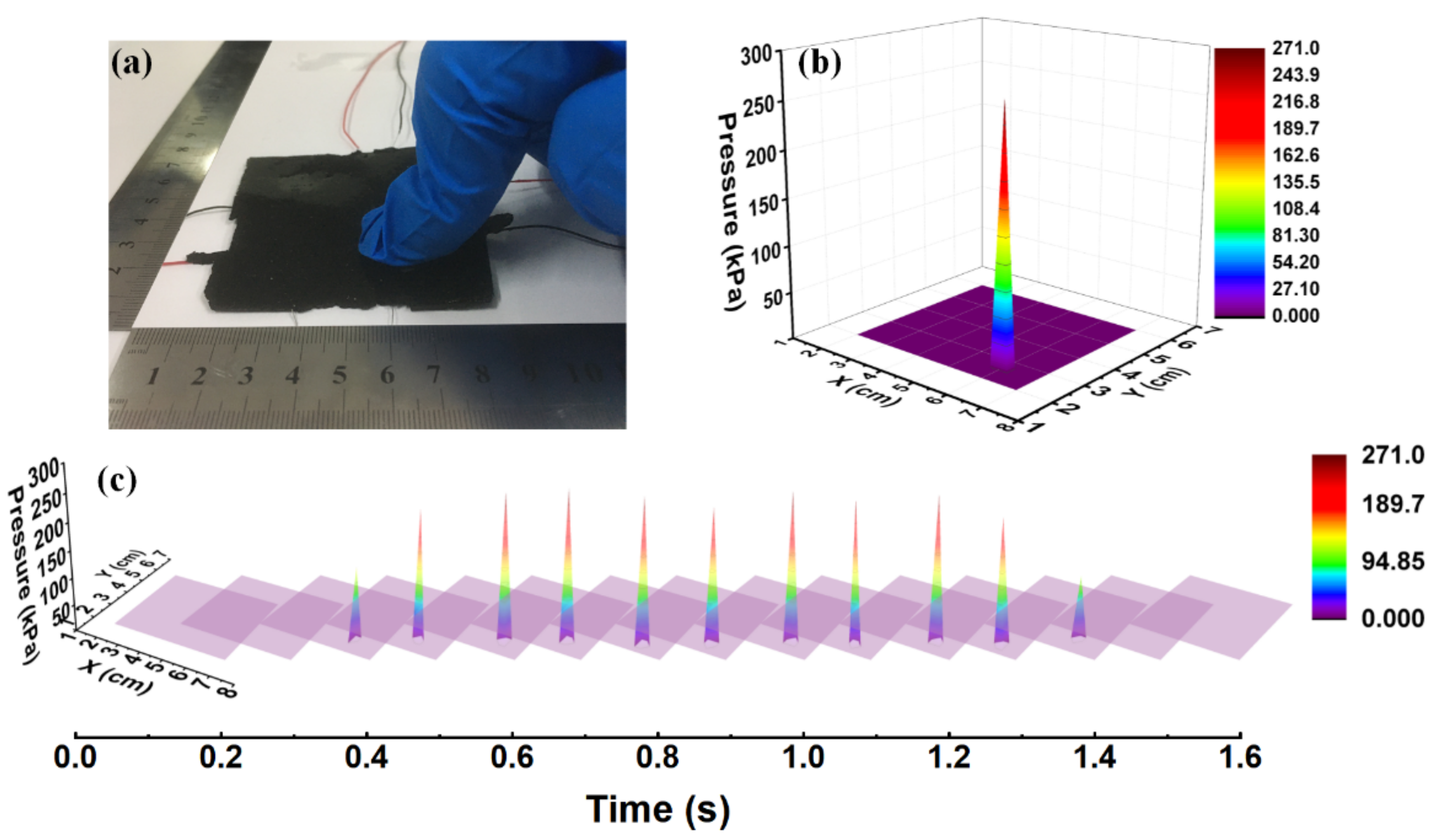
5. Application Examples
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, T.; Jiang, X.; Zhong, Y.; Zhao, X.; Lin, S.; Li, J.; Li, X.; Xu, J.; Li, Z.; Zhu, H. A wearable and highly sensitive graphene strain sensor for precise home-based pulse wave monitoring. ACS Sens. 2017, 2, 967–974. [Google Scholar] [CrossRef]
- Jiang, X.-Z.; Sun, Y.-J.; Fan, Z.; Zhang, T.-Y. Integrated flexible, waterproof, transparent, and self-powered tactile sensing panel. ACS Nano 2016, 10, 7696–7704. [Google Scholar] [CrossRef] [PubMed]
- Rida, I.; Almaadeed, S.; Bouridane, A. Gait recognition based on modified phase-only correlation. Signal Image Video Process. 2016, 10, 463–470. [Google Scholar] [CrossRef]
- Wan, Y.; Wang, Y.; Guo, C.F. Recent progresses on flexible tactile sensors. Mater. Today Phys. 2017, 1, 61–73. [Google Scholar] [CrossRef]
- Hammock, M.L.; Chortos, A.; Tee, B.C.-K.; Tok, J.B.-H.; Bao, Z. 25th anniversary article: The evolution of electronic skin (e-skin): A brief history, design considerations, and recent progress. Adv. Mater. 2013, 25, 5997–6038. [Google Scholar] [CrossRef] [PubMed]
- Rida, I.; Jiang, X.; Marcialis, G.L. Human body part selection by group lasso of motion for model-free gait recognition. IEEE Signal Process. Lett. 2015, 23, 154–158. [Google Scholar] [CrossRef]
- Lee, J.; Sul, H.; Lee, W.; Pyun, K.R.; Ha, I.; Kim, D.; Park, H.; Eom, H.; Yoon, Y.; Jung, J.; et al. Stretchable Skin-Like Cooling/Heating Device for Reconstruction of Artificial Thermal Sensation in Virtual Reality. Adv. Funct. Mater. 2020, 30, 1909171. [Google Scholar] [CrossRef]
- Wang, C.; Dong, L.; Peng, D.; Pan, C. Tactile sensors for advanced intelligent systems. Adv. Intell. Syst. 2019, 1, 1900090. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Dong, L.; Peng, D.; Pan, C. Self-powered tactile sensor array systems based on the triboelectric effect. Adv. Funct. Mater. 2019, 29, 1806379. [Google Scholar]
- Medina, O.; Yozevitch, R.; Shvalb, N. Synthetic Sensor Array Training Sets for Neural Networks. J. Sens. 2019, 2019, 9254315. [Google Scholar] [CrossRef]
- Yang, Z.W.; Pang, Y.; Zhang, L.; Lu, C.; Chen, J.; Zhou, T.; Zhang, C.; Wang, Z.L. Tribotronic transistor array as an active tactile sensing system. ACS Nano 2016, 10, 10912–10920. [Google Scholar] [CrossRef] [PubMed]
- Ma, Y.; Liu, N.; Li, L.; Hu, X.; Zou, Z.; Wang, J.; Luo, S.; Gao, Y. A highly flexible and sensitive piezoresistive sensor based on MXene with greatly changed interlayer distances. Nat. Commun. 2017, 8, 1207. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Zhang, Y.; Zhang, X.; Huo, Z.; Li, X.; Que, M.; Peng, Z.; Wang, H.; Pan, C. A highly stretchable transparent self-powered triboelectric tactile sensor with metallized nanofibers for wearable electronics. Adv. Mater. 2018, 30, 1706738. [Google Scholar]
- Qiao, Y.; Wang, Y.; Tian, H.; Li, M.; Jian, J.; Wei, Y.; Tian, Y.; Wang, D.-Y.; Pang, Y.; Geng, X.; et al. Multilayer graphene epidermal electronic skin. ACS Nano 2018, 12, 8839–8846. [Google Scholar] [CrossRef] [PubMed]
- Chortos, A.; Liu, J.; Bao, Z. Pursuing prosthetic electronic skin. Nat. Mater. 2016, 15, 937–950. [Google Scholar] [CrossRef]
- Kato, Y.; Mukai, T.; Hayakawa, T.; Shibata, T. Tactile Sensor without Wire and Sensing Element in the Tactile Region Based on EIT Method. In Proceedings of the 2007 IEEE Sensors, Atlanta, GA, USA, 28–31 October 2007; pp. 792–795. [Google Scholar]
- Rida, I.; Almaadeed, N.; Almaadeed, S. Robust gait recognition: A comprehensive survey. IET Biom. 2018, 8, 14–28. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, Z.; Huang, X.; You, X.; Ye, J.; Wu, H. A Large-Area, Stretchable, Textile-Based Tactile Sensor. Adv. Mater. Technol. 2020, 5, 1901060. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, J.; Wang, H.; Huang, S.; Wu, H. A flexible tactile sensor with irregular planar shape based on uniform electric field. Sensors 2018, 18, 4445. [Google Scholar] [CrossRef] [Green Version]
- Cheney, M.; Isaacson, D.; Newell, J.C. Electrical impedance tomography. SIAM Rev. 1999, 41, 85–101. [Google Scholar] [CrossRef] [Green Version]
- Frerichs, I.; Amato, M.B.P.; Van Kaam, A.H.; Tingay, D.G.; Zhao, Z.; Grychtol, B.; Bodenstein, M.; Gagnon, H.; Böhm, S.H.; Teschner, E.; et al. Chest electrical impedance tomography examination, data analysis, terminology, clinical use and recommendations: Consensus statement of the TRanslational EIT developmeNt stuDy group. Thorax 2017, 72, 83–93. [Google Scholar] [CrossRef] [Green Version]
- Thomas, A.; Kim, J.; Tallman, T.; Bakis, C. Damage detection in self-sensing composite tubes via electrical impedance tomography. Compos. Part B Eng. 2019, 177, 107276. [Google Scholar] [CrossRef]
- Russo, S.; Nefti-Meziani, S.; Carbonaro, N.; Tognetti, A. A quantitative evaluation of drive pattern selection for optimizing EIT-based stretchable sensors. Sensors 2017, 17, 1999. [Google Scholar] [CrossRef] [PubMed]
- Duan, X.; Taurand, S.; Soleimani, M. Artificial skin through super-sensing method and electrical impedance data from conductive fabric with aid of deep learning. Sci. Rep. 2019, 9, 8831. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar]
- Yu, R.; An, X.; Jin, B.; Shi, J.; Move, O.A.; Liu, Y. Particle classification optimization-based BP network for telecommunication customer churn prediction. Neural Comput. Appl. 2018, 29, 707–720. [Google Scholar] [CrossRef]
- Geng, X.; Lu, S.; Jiang, M.; Sui, Q.; Lv, S.; Xiao, H.; Jia, Y.; Jia, L. Research on FBG-based CFRP structural damage identification using BP neural network. Photonic Sens. 2018, 8, 168–175. [Google Scholar] [CrossRef] [Green Version]
- Wen, H.; Xie, W.; Pei, J.; Guan, L. An incremental learning algorithm for the hybrid RBF-BP network classifier. EURASIP J. Adv. Signal Process. 2016, 2016, 57. [Google Scholar] [CrossRef] [Green Version]
- Li, N.; Yang, D.; Jiang, L.; Liu, H.; Cai, H. Combined use of FSR sensor array and SVM classifier for finger motion recognition based on pressure distribution map. J. Bionic Eng. 2012, 9, 39–47. [Google Scholar] [CrossRef]
- Zhang, R.; Duan, Y.; Zhao, Y.; He, X. Temperature compensation of Elasto-Magneto-Electric (EME) sensors in cable force monitoring using BP Neural Network. Sensors 2018, 18, 2176. [Google Scholar] [CrossRef] [Green Version]
- Sheela, K.G.; Deepa, S.N. Review on methods to fix number of hidden neurons in neural networks. Math. Probl. Eng. 2013, 2013, 425740. [Google Scholar] [CrossRef] [Green Version]




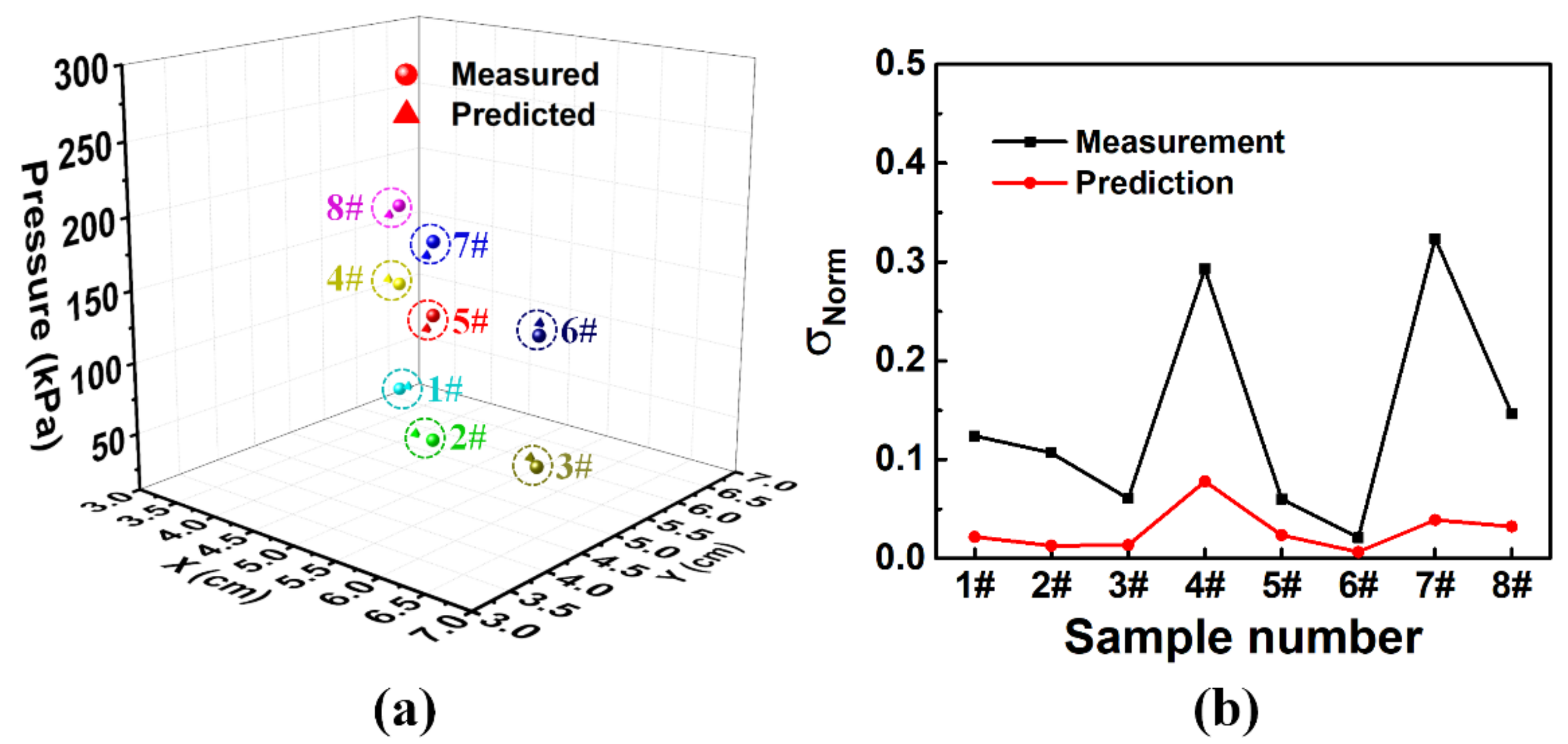



| Selected Point (#) | Coordinates | Pressure (kPa) | |
|---|---|---|---|
| X (cm) | Y (cm) | ||
| 1 | 6.5 | 4.5 | 58.6 |
| 2 | 5.4 | 4.4 | 59.2 |
| 3 | 4.3 | 5.2 | 61.4 |
| 4 | 6.5 | 4.5 | 145.4 |
| 5 | 5.4 | 4.4 | 144.3 |
| 6 | 4.3 | 5.2 | 137.9 |
| 7 | 5.4 | 4.4 | 193.3 |
| 8 | 4.3 | 5.2 | 193.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Cheng, X.; Zhang, W.; Gao, J.; Dai, Y.; Gu, W. A General Grid-Less Design Method for Location and Pressure Sensors with High Precision. Sensors 2020, 20, 7286. https://doi.org/10.3390/s20247286
Zhu X, Cheng X, Zhang W, Gao J, Dai Y, Gu W. A General Grid-Less Design Method for Location and Pressure Sensors with High Precision. Sensors. 2020; 20(24):7286. https://doi.org/10.3390/s20247286
Chicago/Turabian StyleZhu, Xiaobo, Xiong Cheng, Weidong Zhang, Jiale Gao, Yijie Dai, and Wenhua Gu. 2020. "A General Grid-Less Design Method for Location and Pressure Sensors with High Precision" Sensors 20, no. 24: 7286. https://doi.org/10.3390/s20247286
APA StyleZhu, X., Cheng, X., Zhang, W., Gao, J., Dai, Y., & Gu, W. (2020). A General Grid-Less Design Method for Location and Pressure Sensors with High Precision. Sensors, 20(24), 7286. https://doi.org/10.3390/s20247286