An Integrated Positioning and Attitude Determination System for Immersed Tunnel Elements: A Simulation Study
Abstract
:1. Introduction
2. Integrated Positioning and Attitude Determination System of Element Immersion
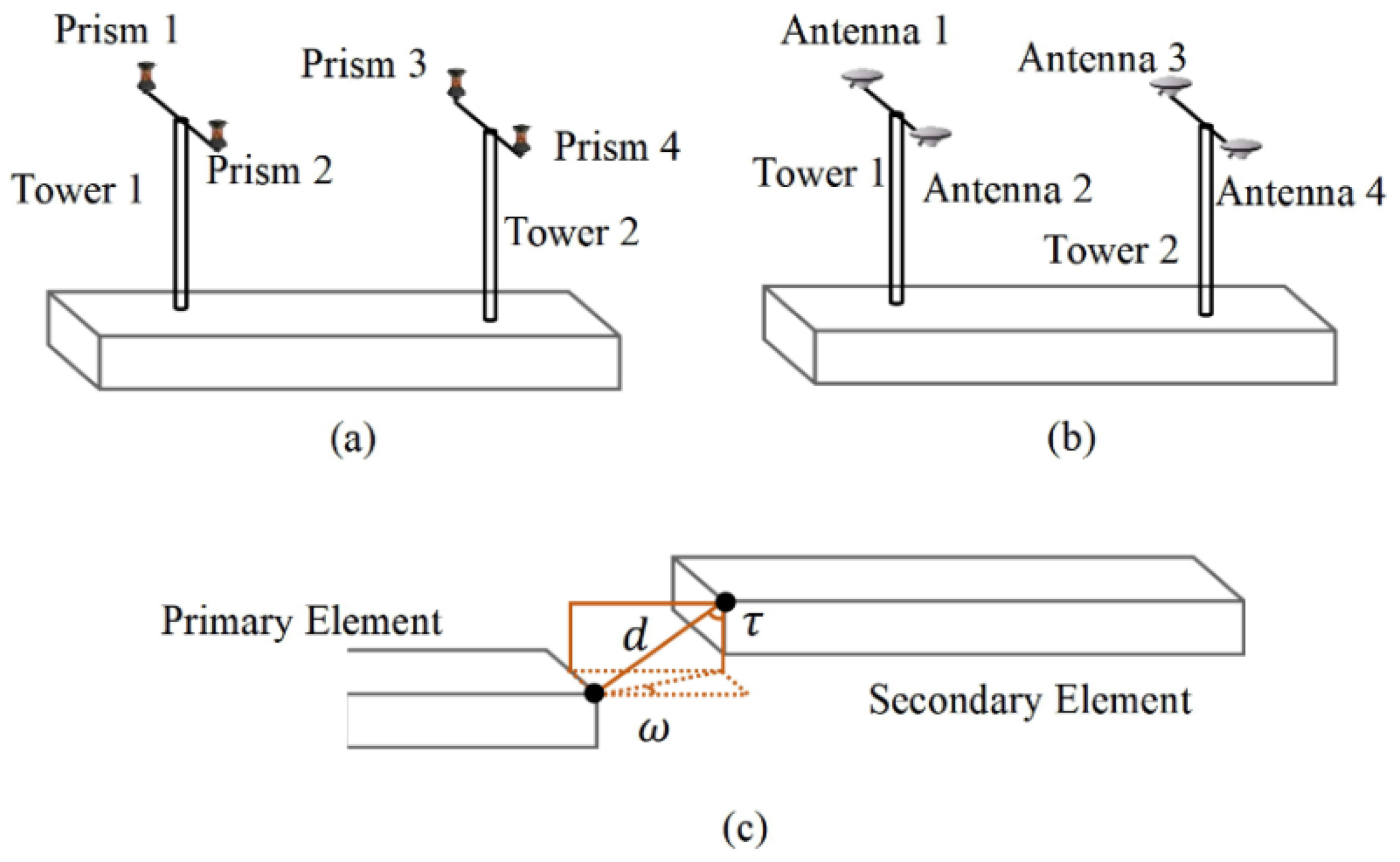
2.1. Coordinate Systems
2.2. Sensors System
2.3. Estimation of Parameters
2.3.1. Definition of Parameters
- : coordinate of antenna 1 in WGS84;
- : roll, pitch and yaw angle of the element.
2.3.2. Functional Model of Positioning and Attitude Determination
- : coordinate of antenna 1 in WGS84 measured by GNSS
- : baseline in WGS84 measured by GNSS
- : baseline in WGS84 measured by GNSS
- : spatial distances measured by the acoustic system
- : roll and pitch angle of the element measured by the inclinometer
2.3.3. Optimal Estimation of the Parameters
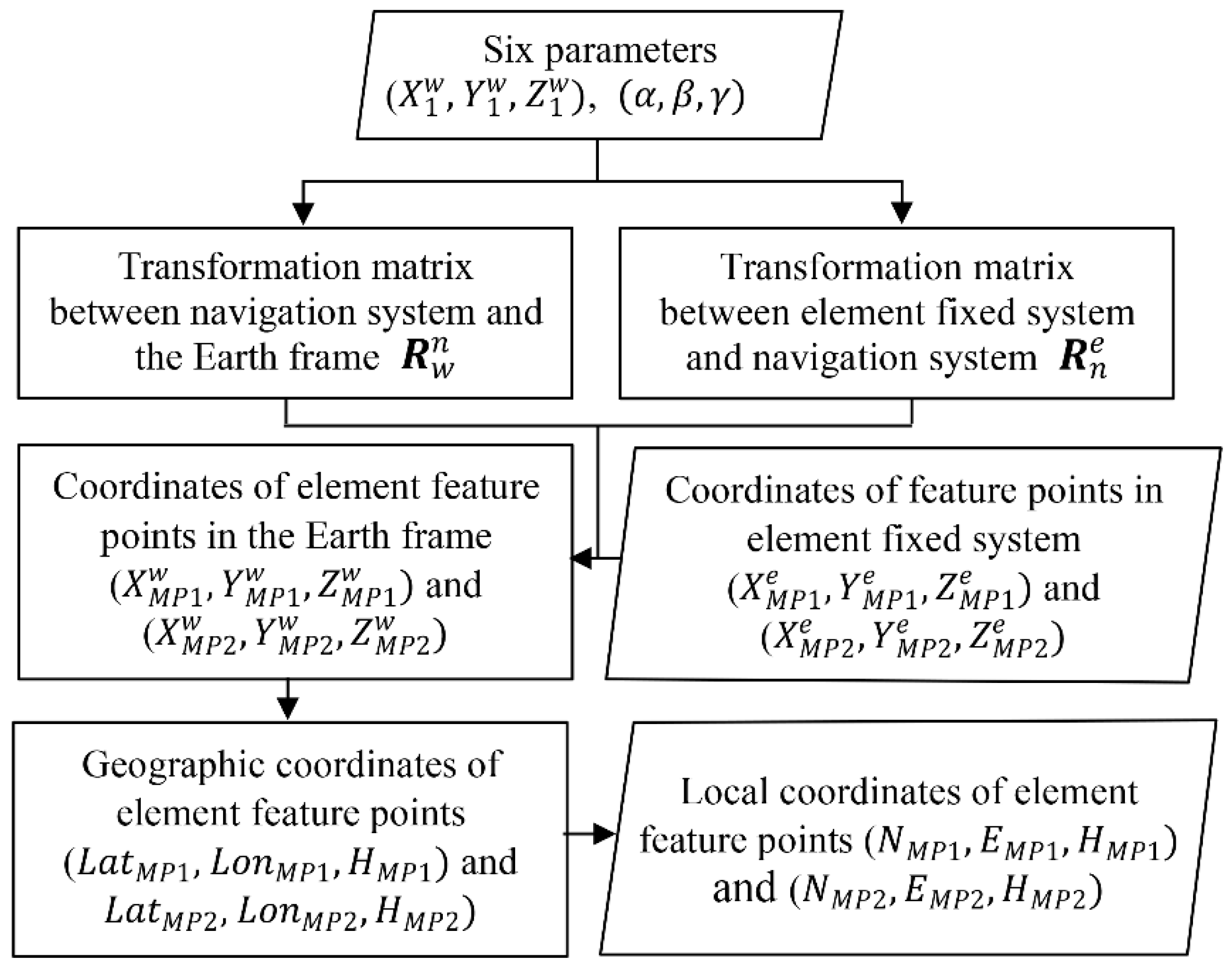
2.4. Coordinate Calculation of Element Feature Points
3. Simulating Errors
3.1. GNSS Errors
3.1.1. GNSS Errors Distribution
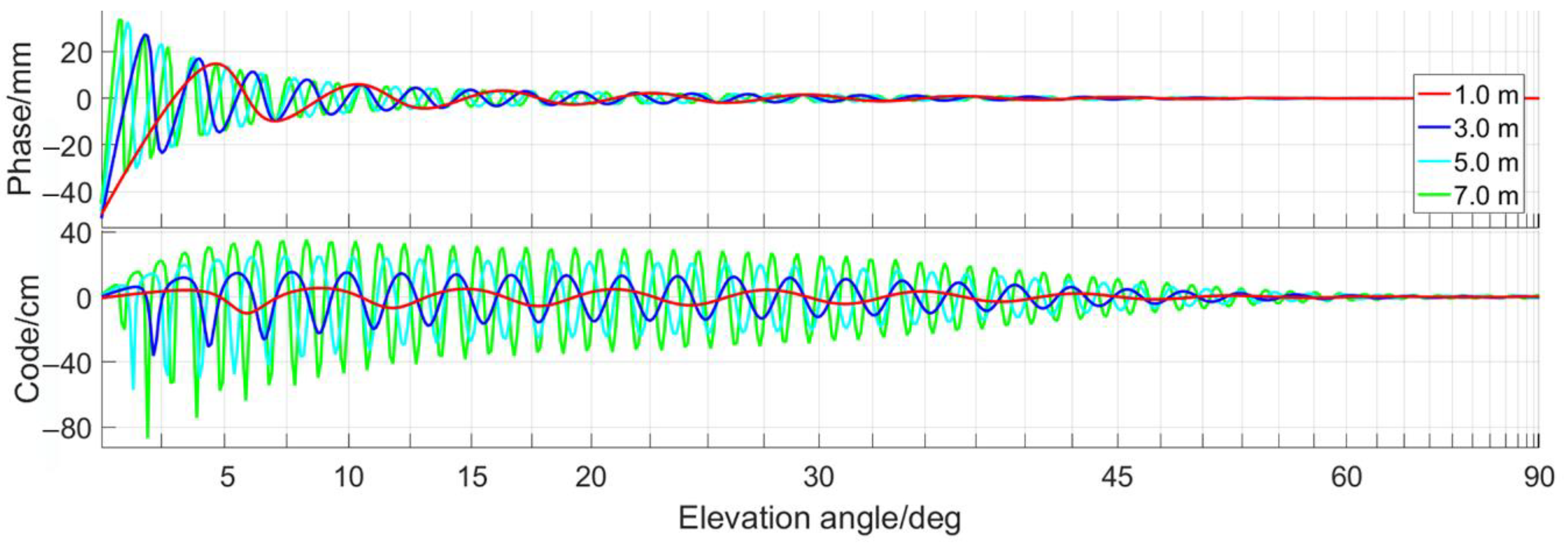
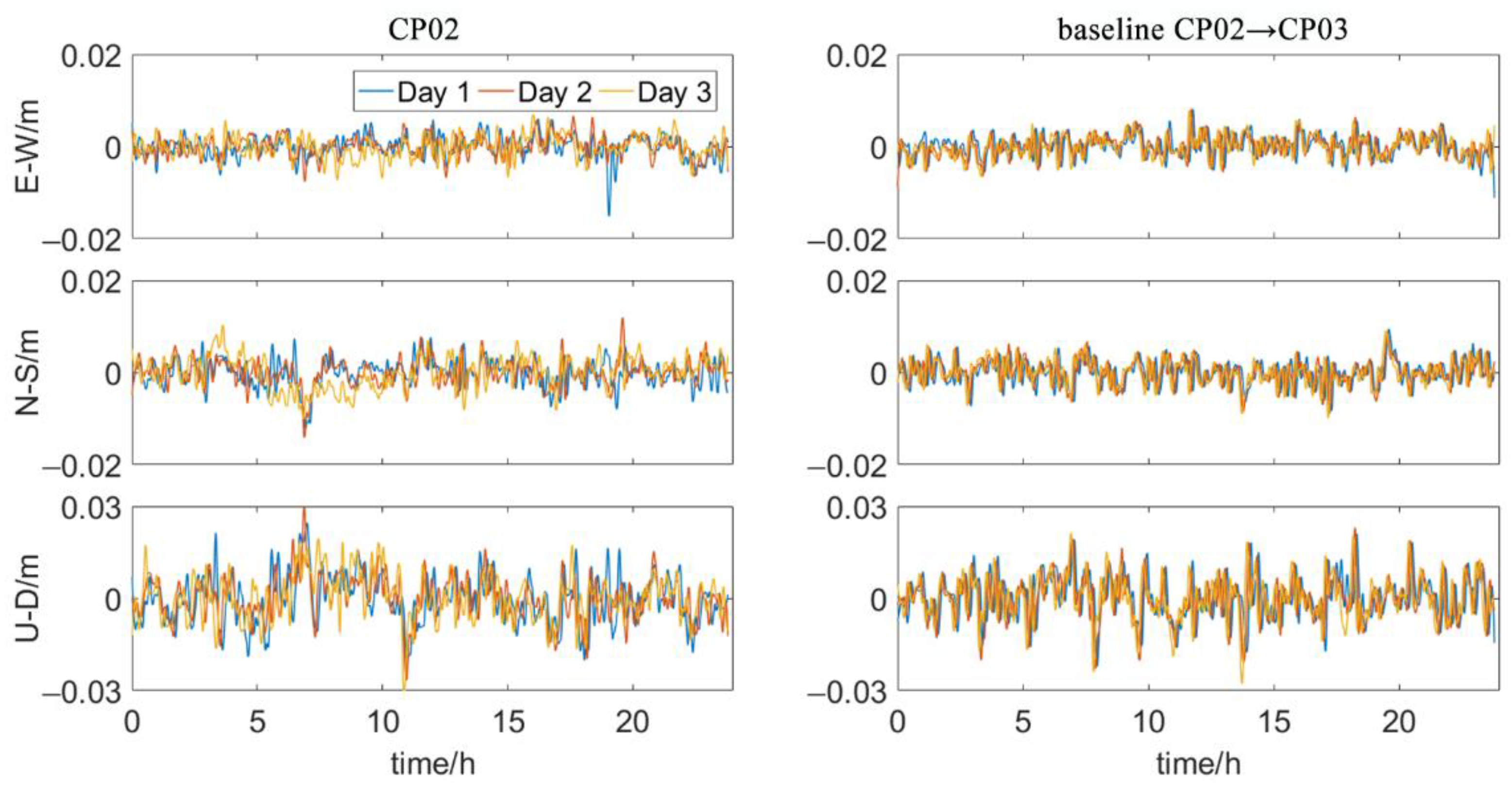
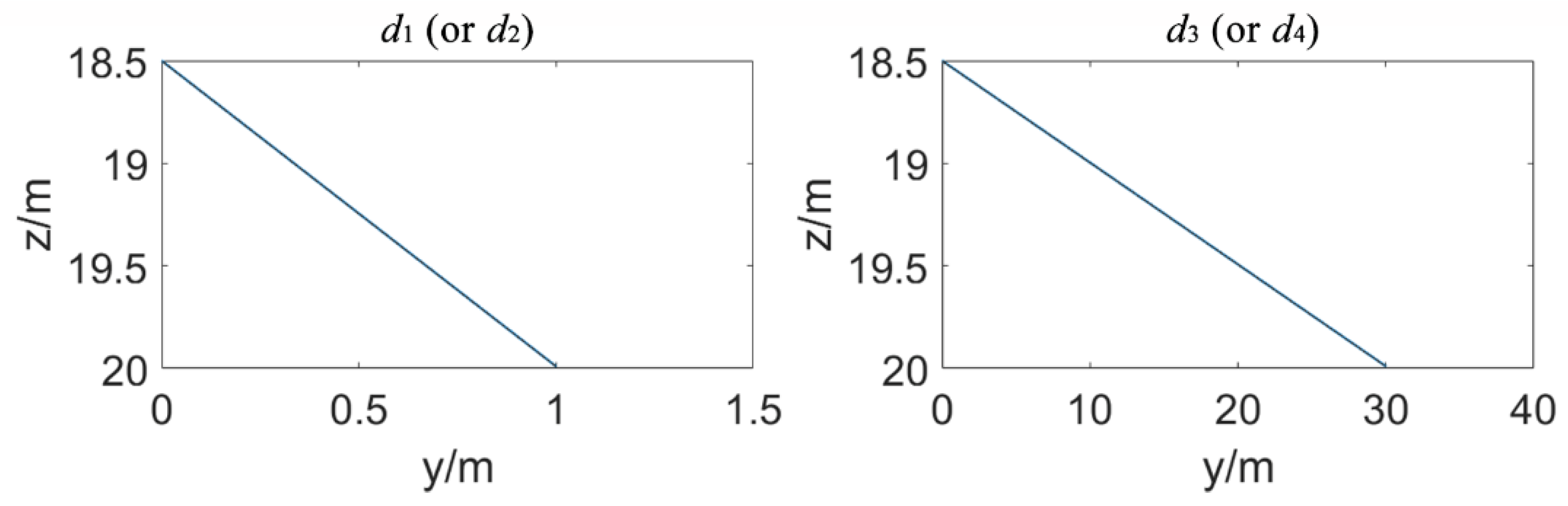
3.1.2. Influence of Multipath Effects
3.2. Roll and Pitch Angle Errors
3.3. Distance Errors
4. Immersed Tunnel Element Immersion Simulation
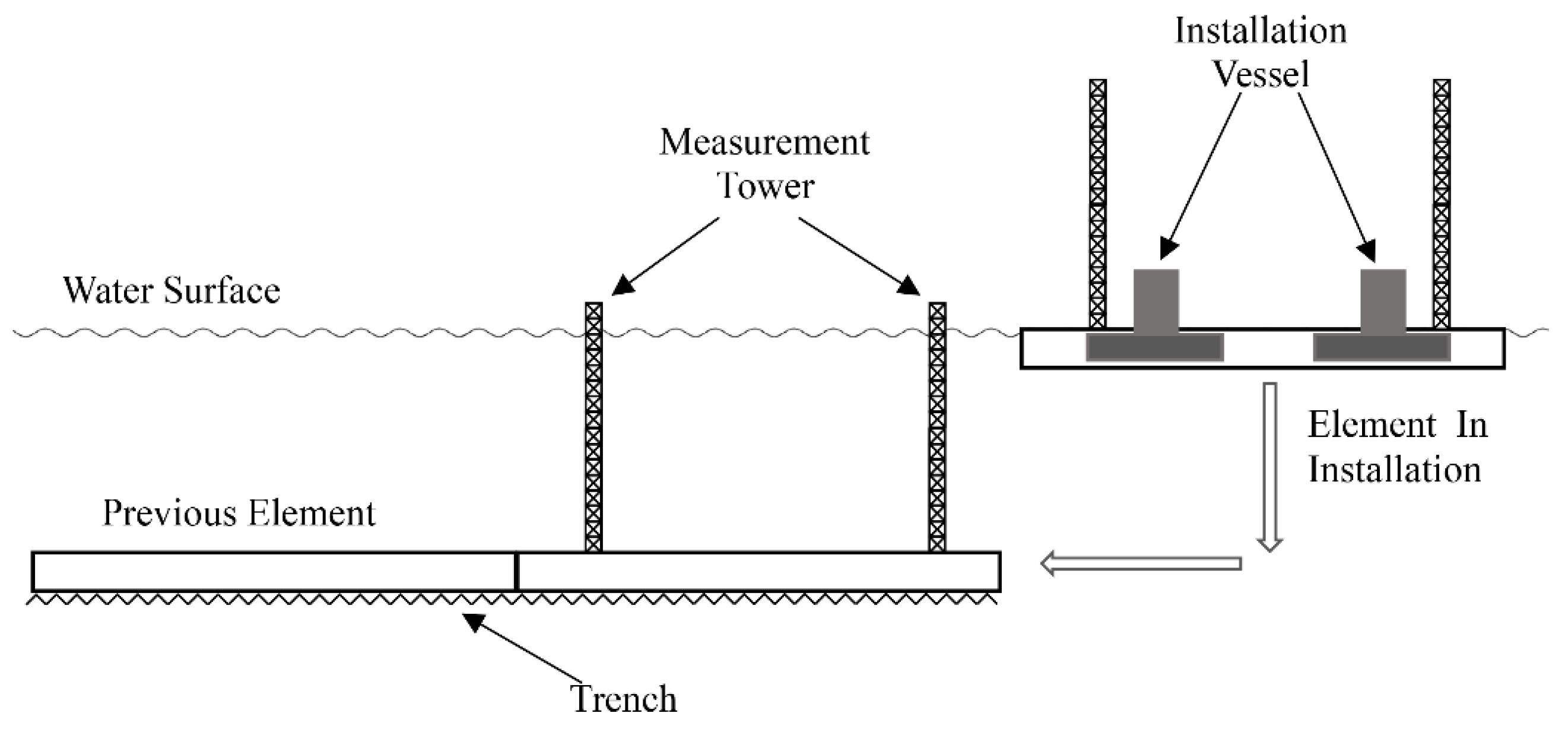
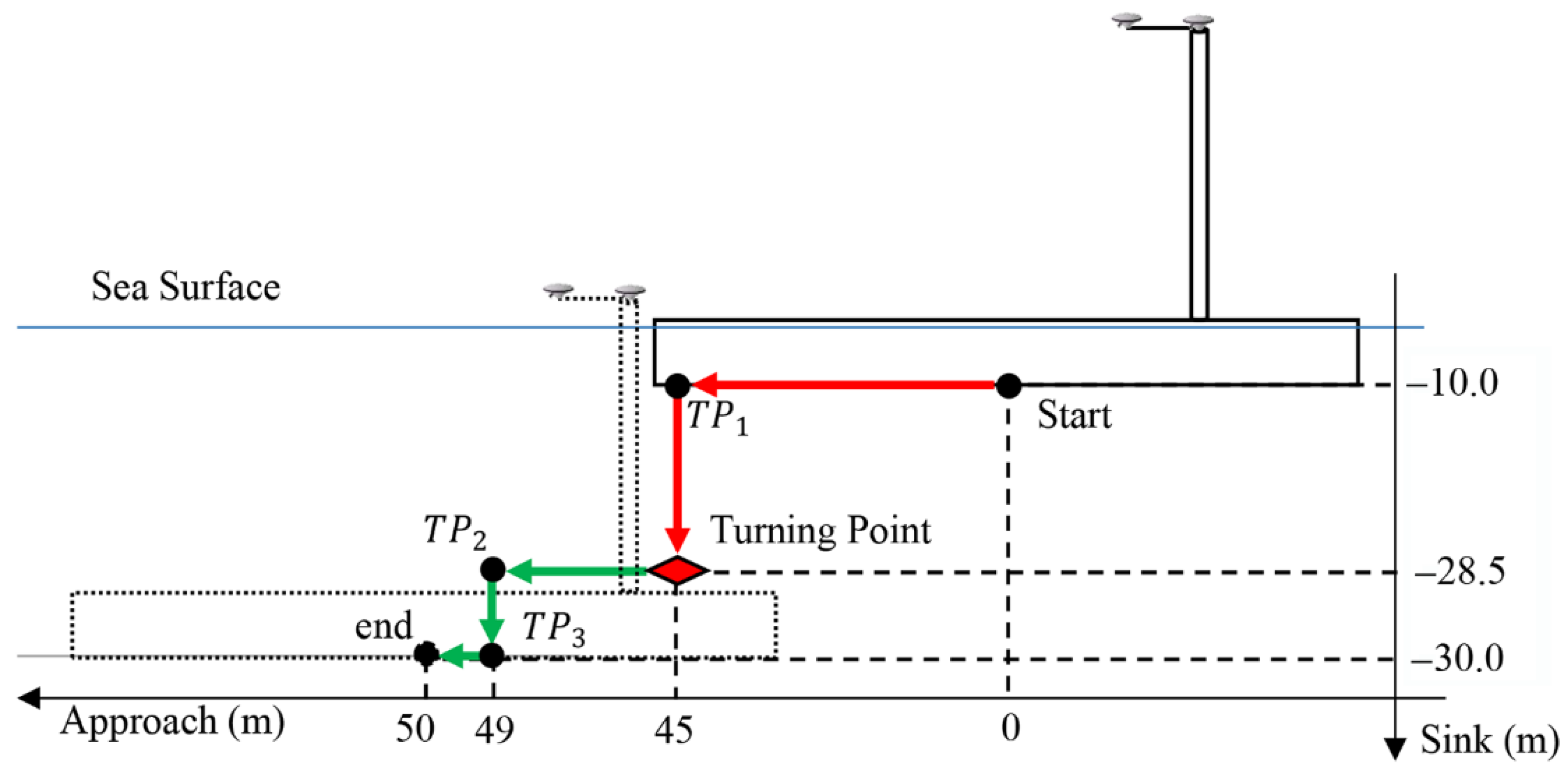
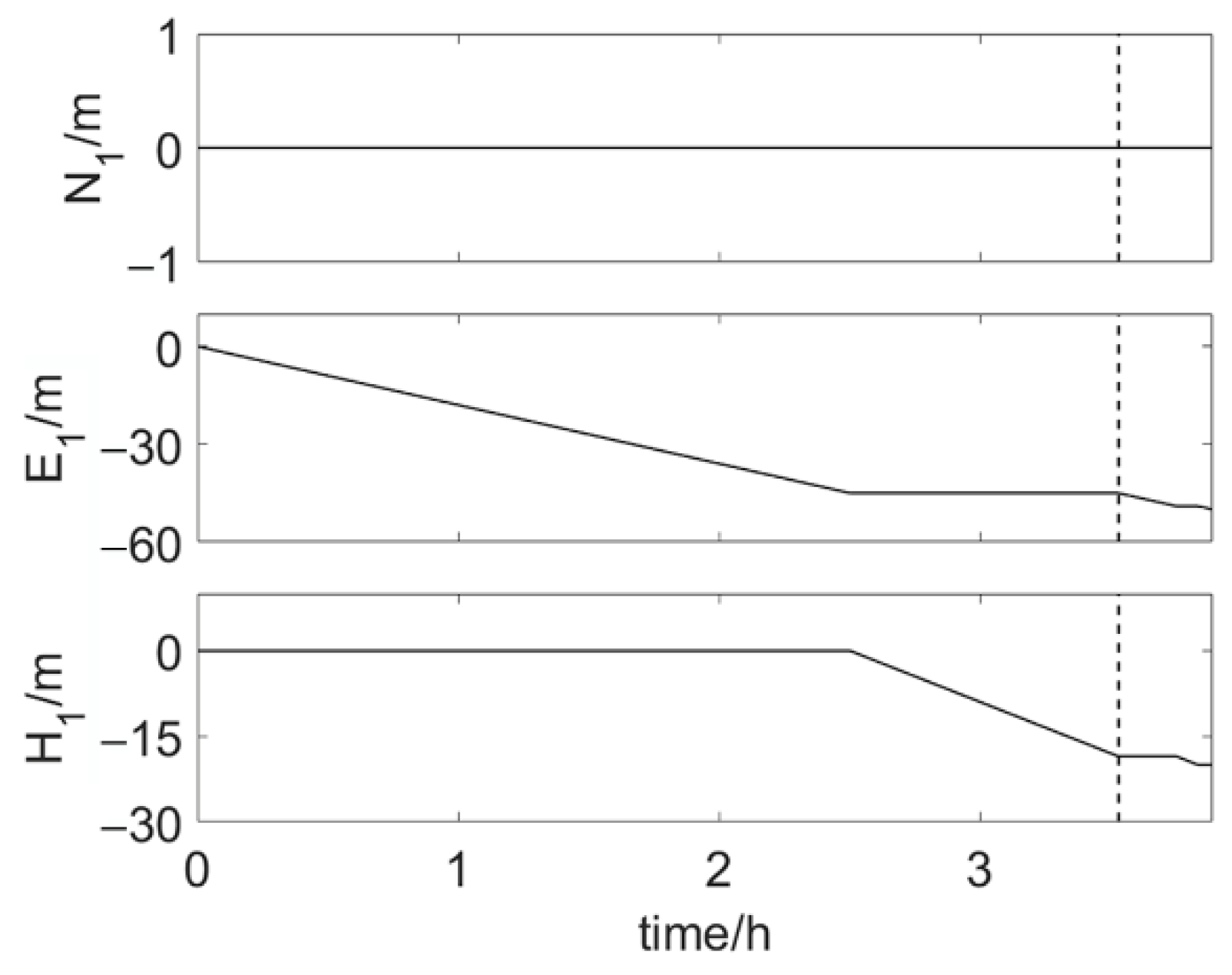
4.1. Installation Scenario
4.2. Observation Error Scenarios
- (1)
- Error scenario 1: only zero mean random errors, no multipath errors or distance systematic errors;
- (2)
- Error scenario 2: multipath error in coordinates of antenna 1, baseline and simultaneously in phase 2 (horizontal 1 cm, vertical 2 cm);
- (3)
- Error scenario 3: multipath error in baseline in phase 2 (horizontal 1 cm, vertical 2 cm);
- (4)
- Error scenario 4: systematic distance errors in phase 2 (1 cm), no multipath errors.
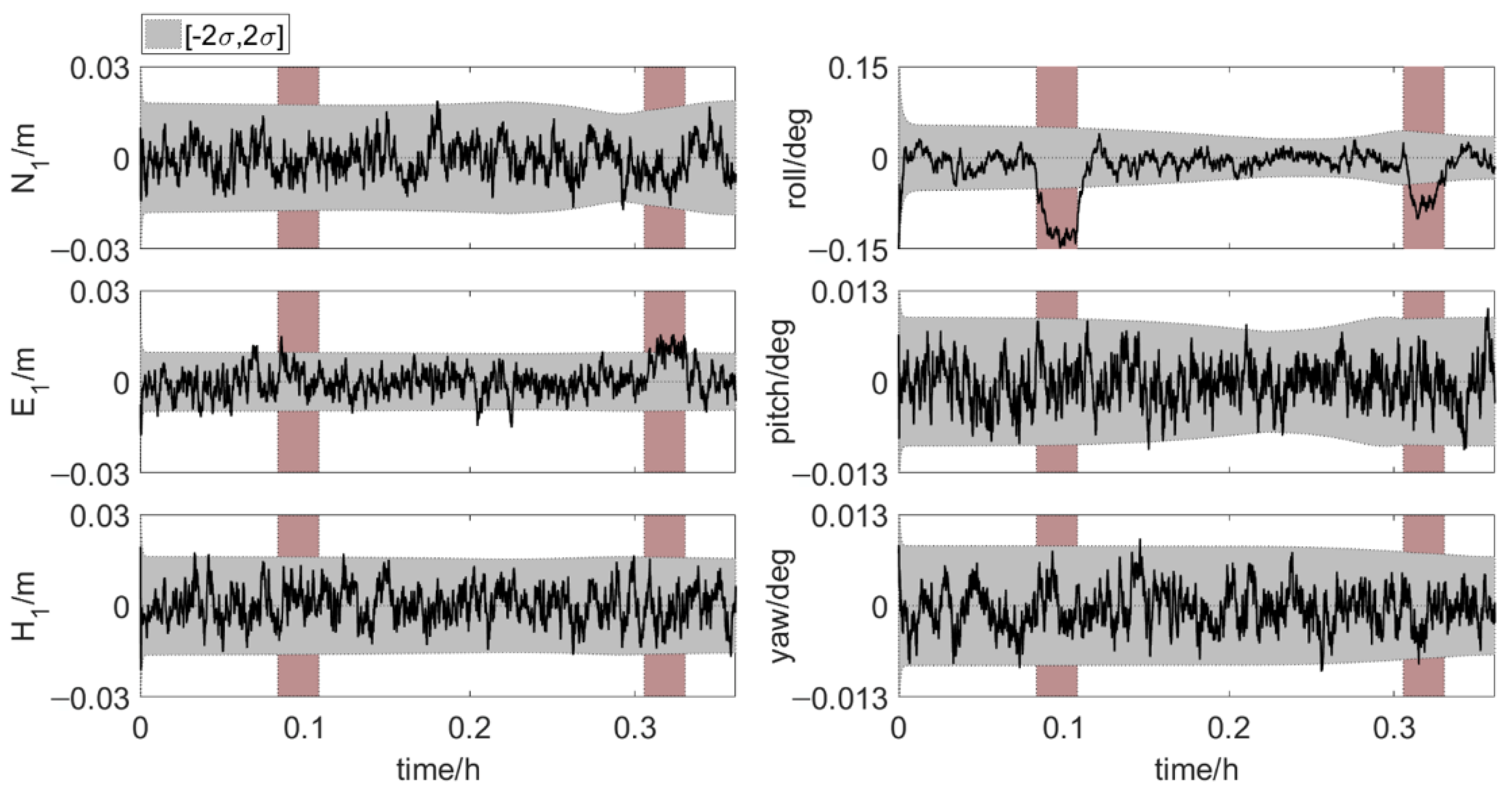
4.3. Results and Discussion
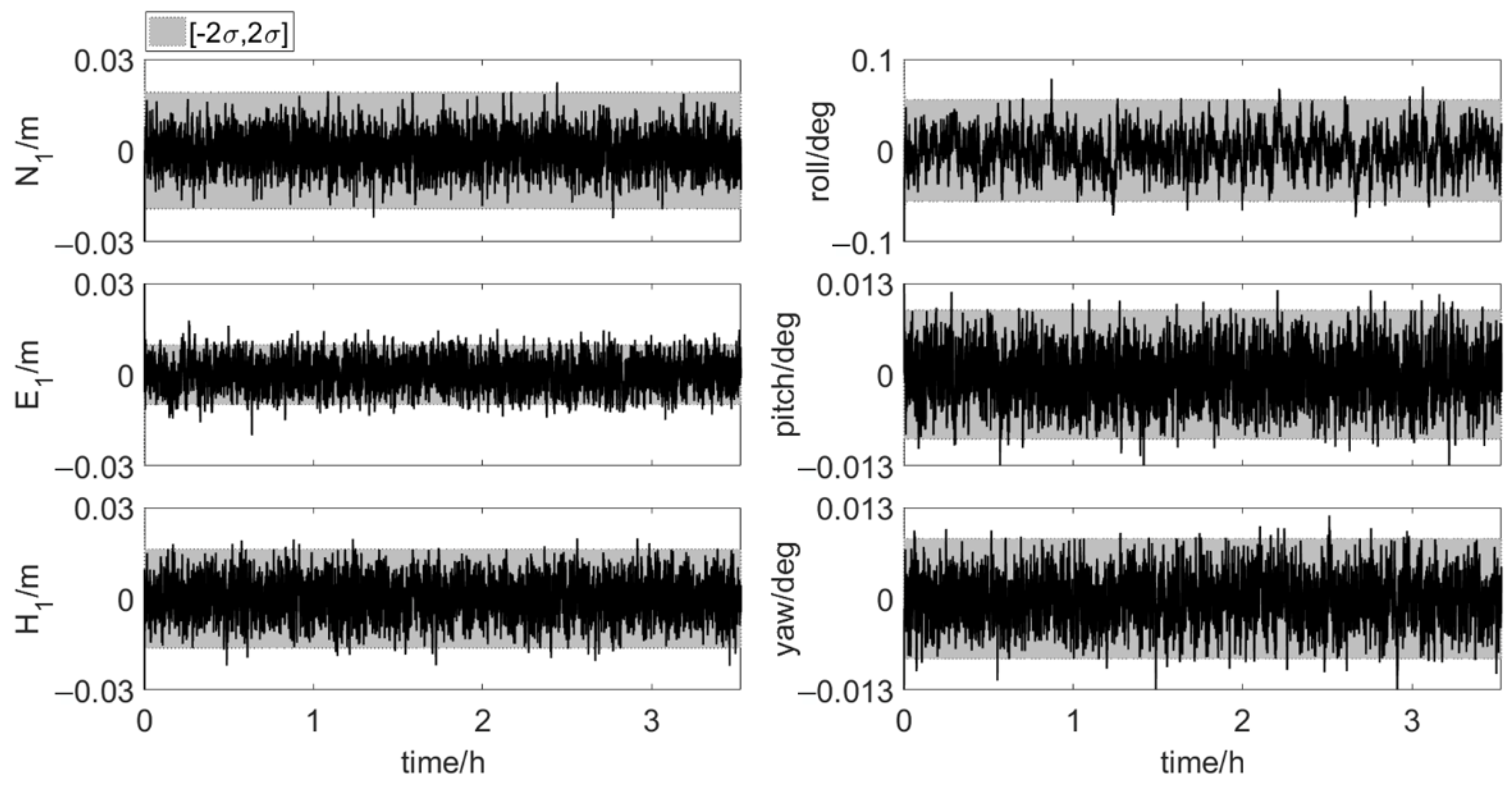
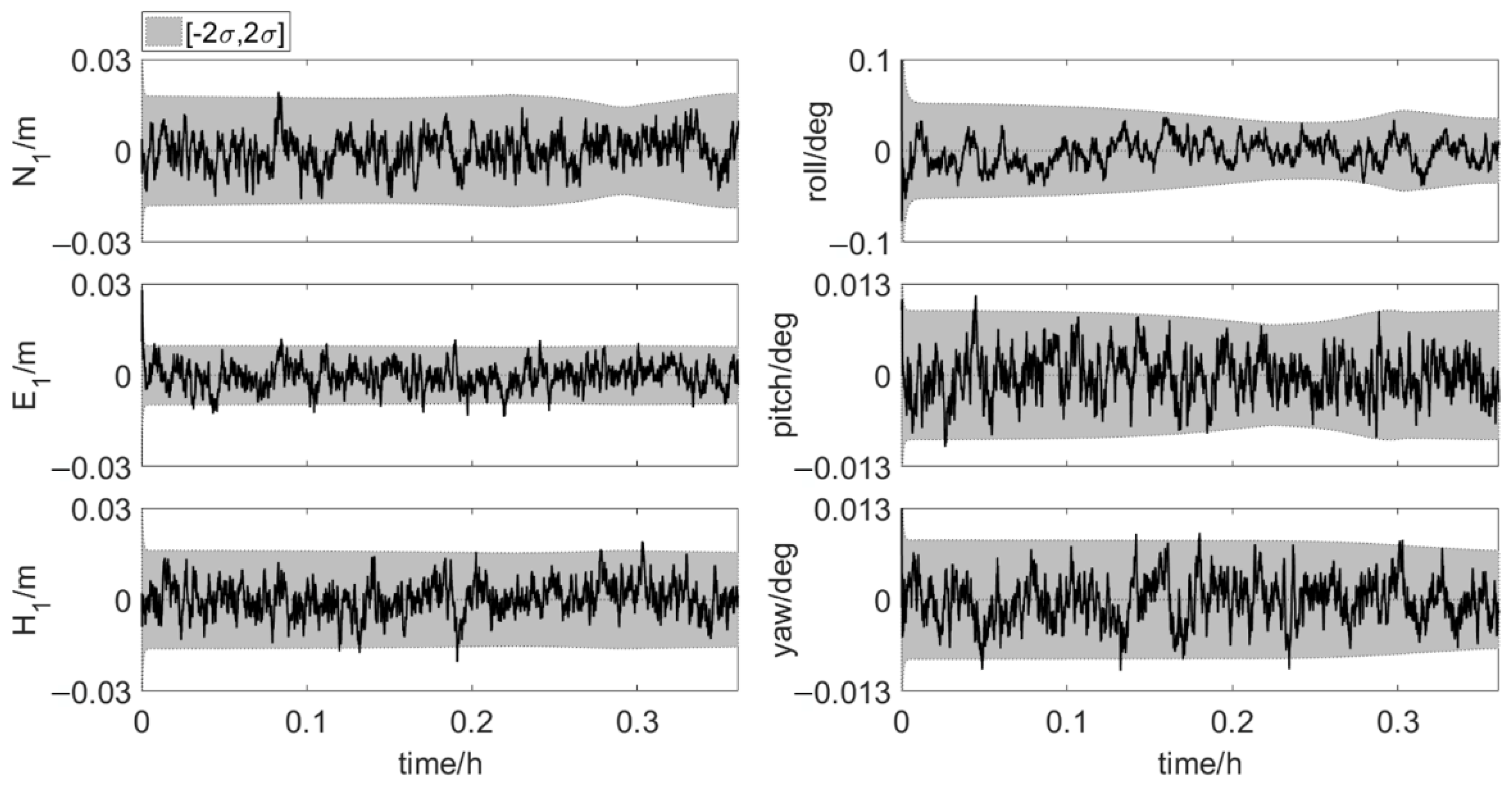
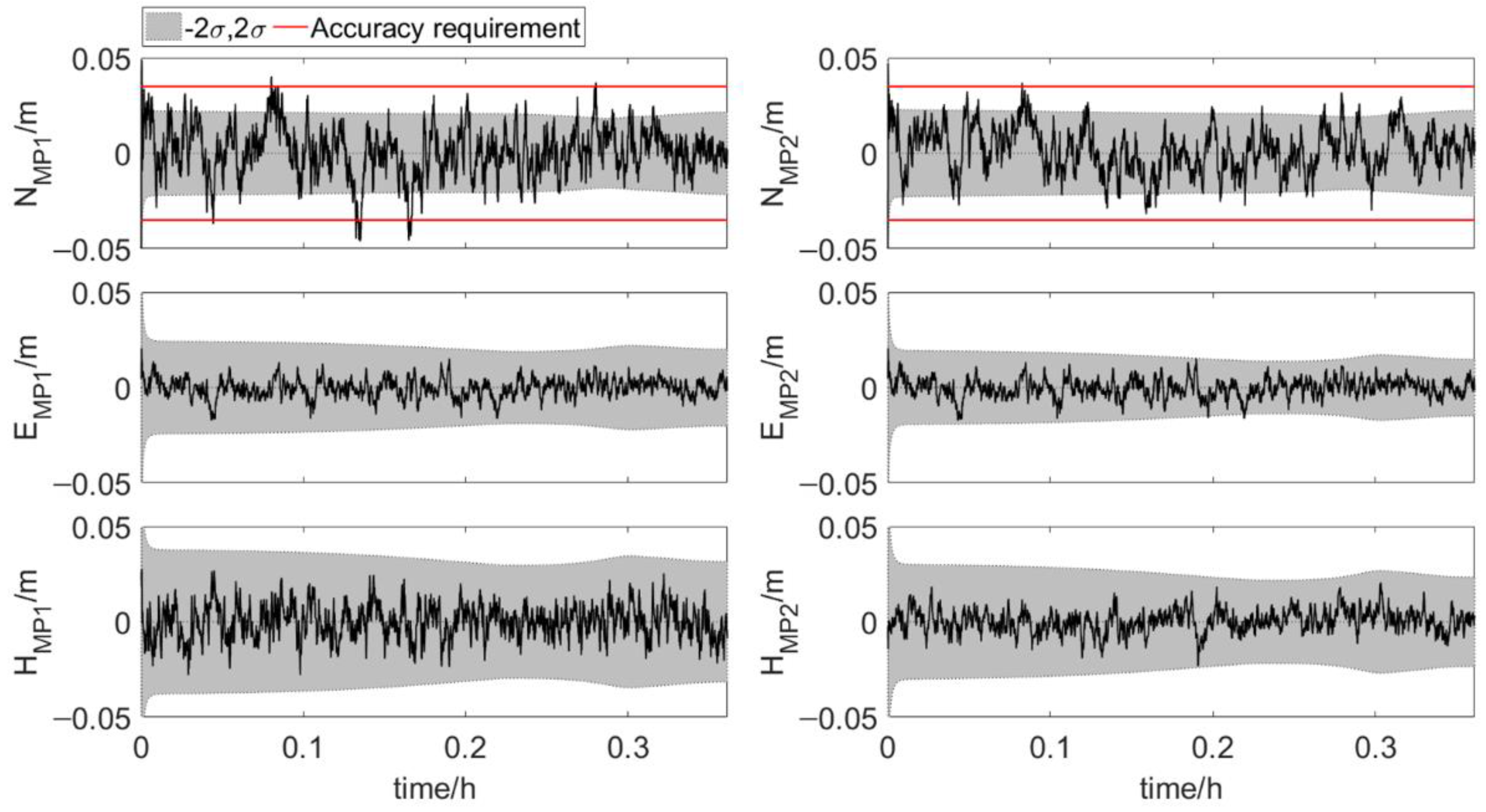
4.3.1. Error Scenario 1
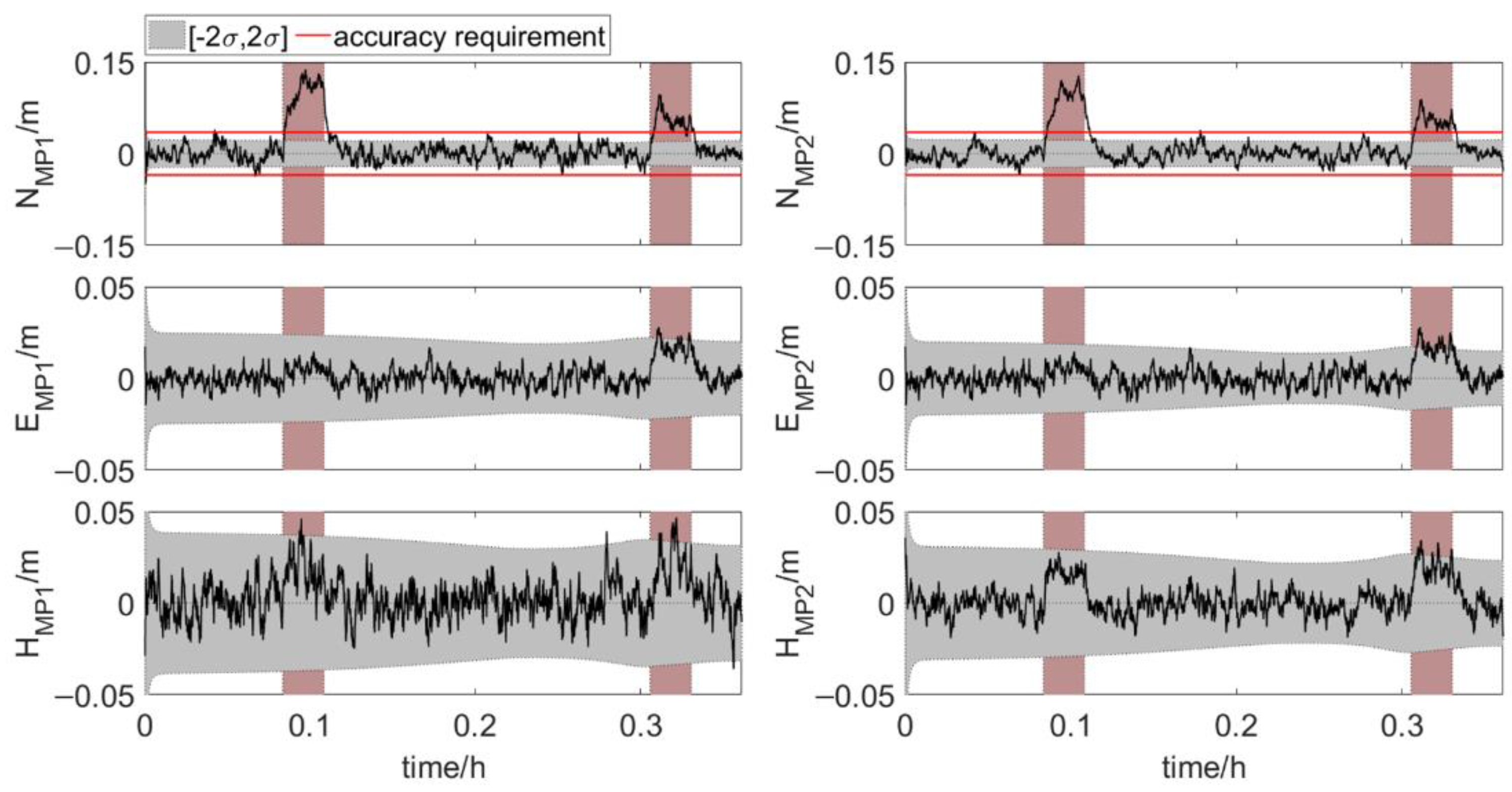
4.3.2. Error Scenario 2 and 3
4.3.3. Error Scenario 4
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- ITA. ITA Working Group 11. An Owners Guide to Immersed and Floating Tunnels. Available online: www.ita-aites.org (accessed on 6 May 2020).
- Marshall, C. The Øresund Tunnel—Making a success of design and build. Tunn. Undergr. Space Technol. 1999, 14, 355–365. [Google Scholar] [CrossRef]
- Janssen, W.; Haas, P.; Yoon, Y. Busan-Geoje Link: Immersed tunnel opening new horizons. Tunn. Undergr. Space Technol. 2006, 21, 332. [Google Scholar] [CrossRef]
- Huang, S.; Li, G.; Wang, X.; Zhang, W. Geodetic network design and data processing for Hong Kong–Zhuhai–Macau link immersed tunnel. Surv. Rev. 2019, 51, 114–122. [Google Scholar] [CrossRef]
- Ren, C.; Lv, H.; Su, L.; Ying, Z. The state of real-time positioning measurement technology for immersed tunnels. Mod. Tunn. Technol. 2012, 49, 44–49. [Google Scholar]
- Fang, C.; Zhao, J. Development of an integrated measurement system used for immersed-tube installation in Guangzhou Zhoutouzui project. China Harb. Eng. 2014, 194, 21–25. [Google Scholar]
- Zhao, K. Research of the Immersed Tube Tunnel Surveying System. Master’s Thesis, South China University of Technology, Guanzhou, China, 2015. [Google Scholar]
- Ruesink, B.; Groot, D. Innovative positioning system integration for immersed tunnel construction. In Proceedings of the Hydro12—Taking Care of the Sea, Rotterdam, The Netherlands, 13–15 November 2012. [Google Scholar]
- Yu, M.; Qi, Q.; Li, T. Applications of acoustic positioning technique in construction of the immersed tunnels. In Proceedings of the Twenty-Fifth International Ocean and Polar Engineering Conference, Kona, HI, USA, 21–26 June 2015. [Google Scholar]
- Van Tol, P. Tunnel Immersion Using Acoustic Positioning. Bachelor’s Thesis, Maritime Instituut Willem Barentsz, Harderwijk, The Netherlands, 2016. [Google Scholar]
- Lu, G. Development of a GPS Multi-Antenna System for Attitude Determination. Ph.D. Thesis, University of Calgary, Calgary, AB, Canada, 1995. [Google Scholar]
- Lachapelle, G.; Cannon, M. Shipborne GPS attitude determination during MMST-93. IEEE J. Ocean. Eng. 1996, 21, 100–104. [Google Scholar] [CrossRef]
- Teunissen, P. The affine constrained GNSS attitude model and its multivariate integer least-squares solution. J. Geod. 2012, 86, 547–563. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Yao, M.; Ma, H.; Jia, W. Low-cost attitude estimation with MIMU and two-antenna GPS for Satcom-on-the-move. GPS Solut. 2013, 17, 75–87. [Google Scholar] [CrossRef]
- Eling, C.; Klingbeil, L.; Kuhlmann, H. Real-time single-frequency GPS/MEMS-IMU attitude determination of lightweight UAVs. Sensors 2015, 15, 26212–26235. [Google Scholar] [CrossRef] [Green Version]
- Cai, X.; Hsu, H.; Chai, H.; Ding, L.; Wang, Y. Multi-antenna GNSS and INS integrated position and attitude determination without base station for land vehicles. J. Navig. 2019, 72, 342–358. [Google Scholar] [CrossRef]
- Teunissen, P. The LAMBDA method for the GNSS compass. Artif. Satell. 2006, 41, 89–103. [Google Scholar] [CrossRef] [Green Version]
- Teunissen, P. A general multivariate formulation of the multi-antenna GNSS attitude determination problem. Artif. Satell. 2007, 42, 97–111. [Google Scholar] [CrossRef] [Green Version]
- Buist, P.; Teunissen, P.; Giorgi, G.; Verhagen, S. Multiplatform instantaneous GNSS ambiguity resolution for triple-and quadruple-antenna configurations with constraints. Int. J. Navig. Obs. 2009, 2009, 565426. [Google Scholar] [CrossRef]
- Teunissen, P. Integer least squares theory for the GNSS compass. J. Geod. 2010, 84, 433–447. [Google Scholar] [CrossRef] [Green Version]
- Chui, C.K.; Chen, G. Orthogonal projection and Kalman Filter. In Kalman Filtering; Springer: Cham, Switzerland, 2017; pp. 33–49. [Google Scholar]
- Gacoki, T.; Aduol, F. Transformation between GPS coordinates and local plane UTM coordinates using the Excel spreadsheet. Emp. Surv. Rev. 2002, 36, 449–462. [Google Scholar] [CrossRef]
- Cheng, P.; Cheng, Y.; Wen, H.; Huang, J.; Wang, H.; Wang, G. Practical Manual on CGCS 2000; Surveying and Mapping Publishing House: Beijing, China, 2008; pp. 144–148. [Google Scholar]
- Goh, S.; Low, K. Survey of Global-Positioning-System-Based attitude determination algorithms. J. Guid. Control. Dyn. 2017, 40, 1321–1335. [Google Scholar] [CrossRef]
- Sun, H. Approximate representation of the p-norm distribution. Geomat. Inf. Sci. Wuhan Univ. 2001, 26, 222–225. [Google Scholar]
- Xiong, P. P-norm semiparametric regression model. In Proceedings of the Sixth International Conference on Machine Learning and Cybernetics, Hong Kong, China, 19–22 August 2007. [Google Scholar]
- Lan, Y.; Jia, Y. The study of error distribution for GPS observed values. Bull. Surv. Mapp. 2008, 4, 12–13. [Google Scholar]
- Nievinski, F.G.; Larson, K.M. Forward modeling of GPS multipath for near-surface reflectometry and positioning applications. GPS Solut. 2014, 18, 309–322. [Google Scholar] [CrossRef]
- RTKLIB: An Open Source Program Package for GNSS Positioning. Available online: http://www.rtklib.com/ (accessed on 1 September 2020).
- Kong, X.; Chen, Q.; Wang, J.; Gu, G.; Wang, P.; Qian, W.; Ren, K.; Miao, X. Inclinometer assembly error calibration and horizontal image correction in photoelectric measurement systems. Sensors 2018, 18, 248. [Google Scholar] [CrossRef] [Green Version]
- Wei, X.; Cui, C.; Wang, G.; Wan, X. Autonomous positioning utilizing star sensor and inclinometer. Measurement 2019, 131, 132–142. [Google Scholar] [CrossRef]
- Mezzino, J. Ray acoustical model of the ocean incorporating a sound-velocity profile with a continuous second derivative. J. Acoust. Soc. Am. 1973, 53, 581–589. [Google Scholar] [CrossRef]
- Munk, W. Sound channel in an exponentially stratified ocean, with application to SOFAR. J. Acoust. Soc. Am. 1974, 55, 220–226. [Google Scholar] [CrossRef]
- Davis, T.M.; Countryman, K.; Carron, M. Tailored acoustic products utilizing the NAVOCEANO GDEM (a generalized digital environmental model). In Proceedings of the 36th Naval Symposium on Underwater Acoustics, Naval Ocean Systems Center, San Diego, CA, USA, 19 December 1986. [Google Scholar]
- LeBlanc, L.; Middleton, F. An underwater acoustic sound velocity data model. J. Acoust. Soc. Am. 1980, 67, 2055–2062. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Zhang, J. A new model for calculating sound speed profile structure. Acta Oceanol. Sin. 2011, 33, 54–60. [Google Scholar] [CrossRef]
- Xu, P.; Ando, M.; Tadokoro, K. Precise, three-dimensional seafloor geodetic deformation measurements using difference techniques. Earth Planets Space 2005, 57, 795–808. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.; Wang, Z.; Liu, H. Investigation on underwater positioning stochastic model based on sound ray incidence angle. Acta Geod. Cartogr. Sin. 2018, 47, 1280–1289. [Google Scholar]




| Coordinate System | Definition |
|---|---|
| ECEF Coordinate System | Origin: the earth’s center of mass; Z-axis: the earth’s rotation axis defined by the Conventional Terrestrial Pole; X-axis: the intersection of the orthogonal plane to Z-axis and Greenwich mean meridian; Y-axis: orthogonal to X-axis and Z-axis, making the system directly oriented. |
| Navigation coordinate system | It is formed from a plane tangent to the Earth’s surface. The three axes point east, north and perpendicular to the tangent plane and away from the center of the earth. |
| Element-fixed coordinated system | It is defined by the plane of the upper surface of the element. See in Figure 3. |
| Local plane coordinate and height system | It is realized by Gauss–Krüger or Universal Transverse Mercator projection. The elevations are given as ellipsoidal heights. |
| Distribution | |||
|---|---|---|---|
| Normal distribution | 68.27% | 95.45% | 99.73% |
| -norm distribution | 71.89% | 94.53% | 99.19% |
| (m or °) | Phase 1 | Last Part of Phase 2 | (m) | Phase 1 | Last Part of Phase 2 |
|---|---|---|---|---|---|
| 0.010 | 0.009 | 0.012 | 0.011 | ||
| 0.005 | 0.005 | 0.013 | 0.010 | ||
| 0.010 | 0.008 | 0.020 | 0.016 | ||
| 0.028 | 0.018 | 0.012 | 0.011 | ||
| 0.005 | 0.005 | 0.010 | 0.007 | ||
| 0.005 | 0.004 | 0.016 | 0.012 |
| Element Feature Points | Phase 1 | Phase 2 | ||
|---|---|---|---|---|
| Within Accuracy Requirement | Within | Within Accuracy Requirement | Within | |
| MP1 | 99.9% | 84.6% | 99.9% | 85.2% |
| MP2 | 99.9% | 90.4% | 99.9% | 90.0% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Klingbeil, L.; Zimmermann, F.; Huang, S.; Kuhlmann, H. An Integrated Positioning and Attitude Determination System for Immersed Tunnel Elements: A Simulation Study. Sensors 2020, 20, 7296. https://doi.org/10.3390/s20247296
Li G, Klingbeil L, Zimmermann F, Huang S, Kuhlmann H. An Integrated Positioning and Attitude Determination System for Immersed Tunnel Elements: A Simulation Study. Sensors. 2020; 20(24):7296. https://doi.org/10.3390/s20247296
Chicago/Turabian StyleLi, Guanqing, Lasse Klingbeil, Florian Zimmermann, Shengxiang Huang, and Heiner Kuhlmann. 2020. "An Integrated Positioning and Attitude Determination System for Immersed Tunnel Elements: A Simulation Study" Sensors 20, no. 24: 7296. https://doi.org/10.3390/s20247296
APA StyleLi, G., Klingbeil, L., Zimmermann, F., Huang, S., & Kuhlmann, H. (2020). An Integrated Positioning and Attitude Determination System for Immersed Tunnel Elements: A Simulation Study. Sensors, 20(24), 7296. https://doi.org/10.3390/s20247296






