Time Reverse Modeling of Damage Detection in Underwater Concrete Beams Using Piezoelectric Intelligent Modules
Abstract
1. Introduction
2. Piezoelectric Intelligent Module and Detecting Approach for Cracks
2.1. Piezoelectric Intelligent Module
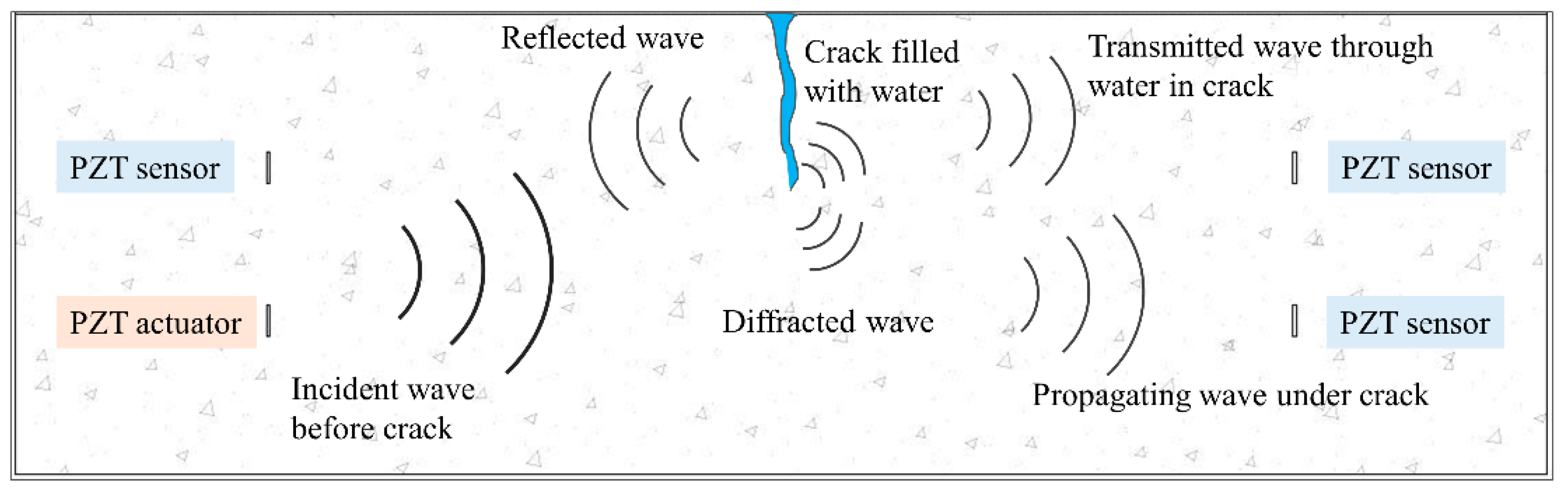
2.2. Wave-Based SHM Method
2.3. Principle of the Time Reversal Method
2.4. Wavelet Packet Decomposition and Damage Index
3. Numerical Modeling Based on the Finite Element Method
3.1. Property and Modeling Principle of Piezoelectric Patch
3.2. Random Aggregates Model
- Step 1
- —estimate the particle size distribution. The random sampling principle of the Monte Carlo method is applied to obtain the particle size distribution in the simulation, following the grading curve with a maximum grain size of 5 mm.
- Step 2
- —determine the geometry of each aggregate. First, a circular particle size is generated with the size from step 1. Then, it is cut into a polygon, whose side length and inner angle are controlled by the irregularity parameter.
- Step 3
- —release the aggregates into the beam. Before placing the aggregates, the beam should be meshed into structured grids. The grid size is considered to be 1mm to achieve a good balance of image resolution and computing cost. The aggregates are then randomly mapped to the grid in the order from large ones to small ones. It is also necessary to check the potential problems, such as aggregate overlap, boundary intersection, and gaps between cement faces. If the above problems occur, the aggregates should be re-dropped.
3.3. Modeling of Wave Propagation
3.3.1. Forward Simulation
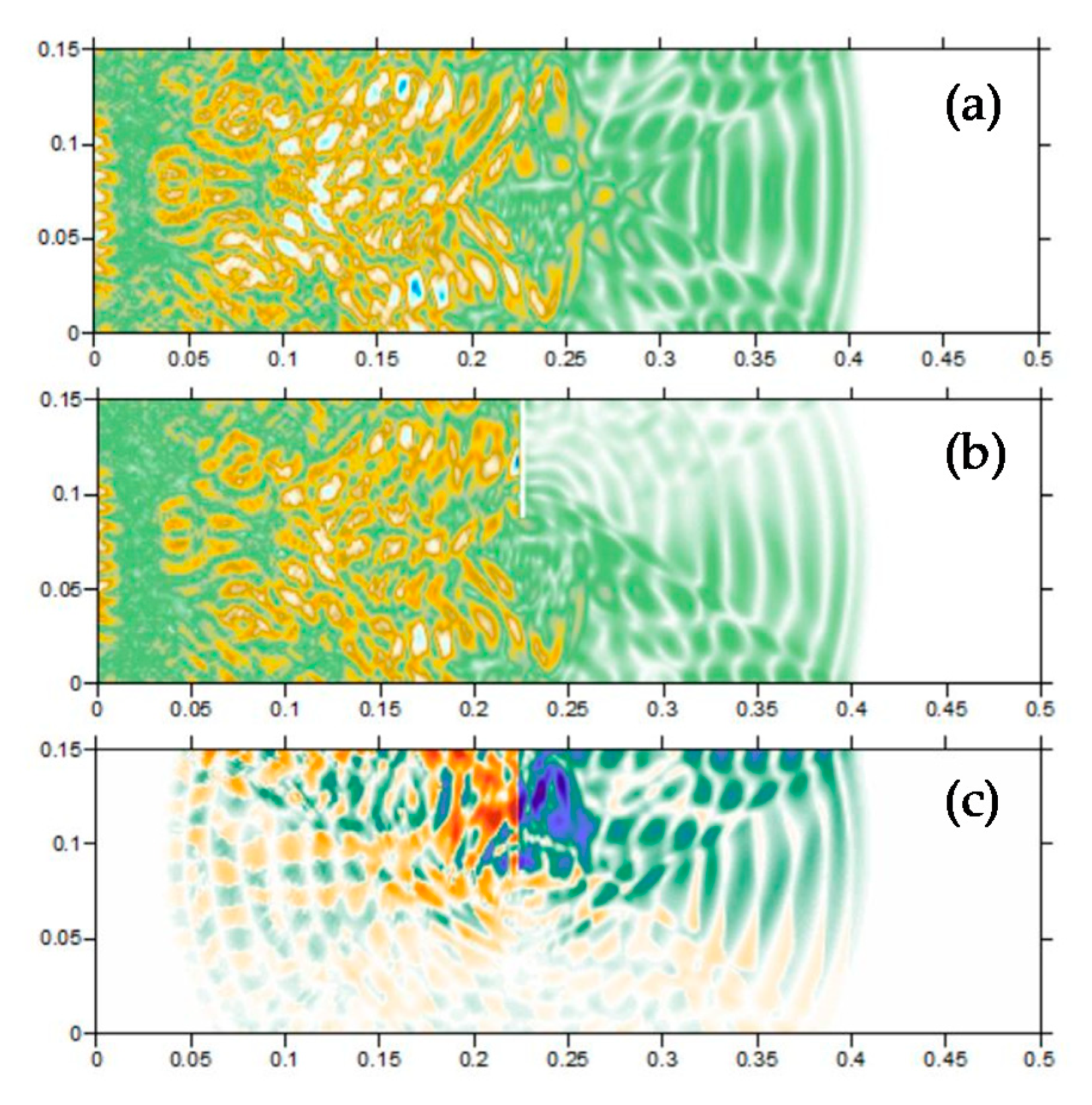
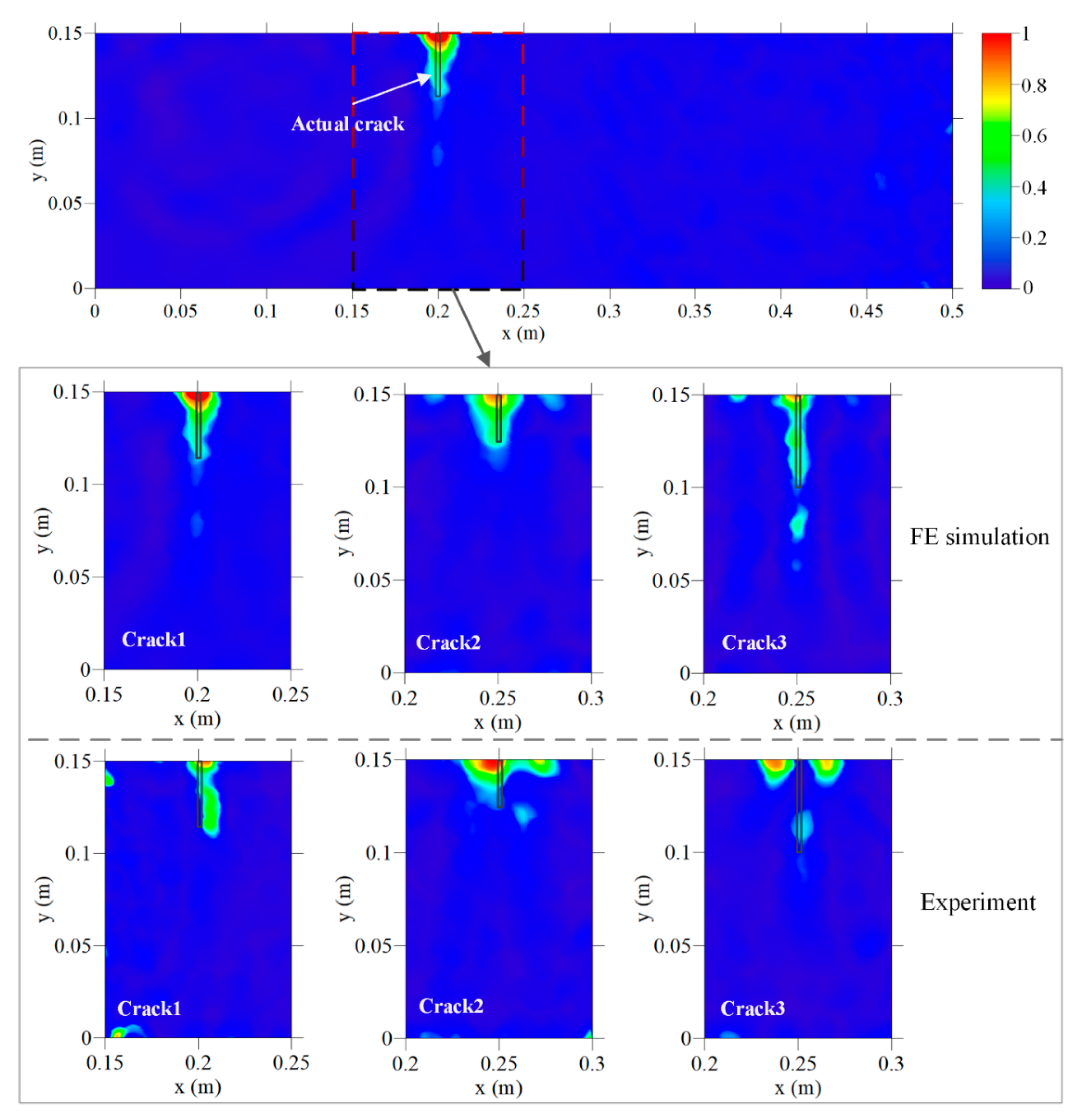
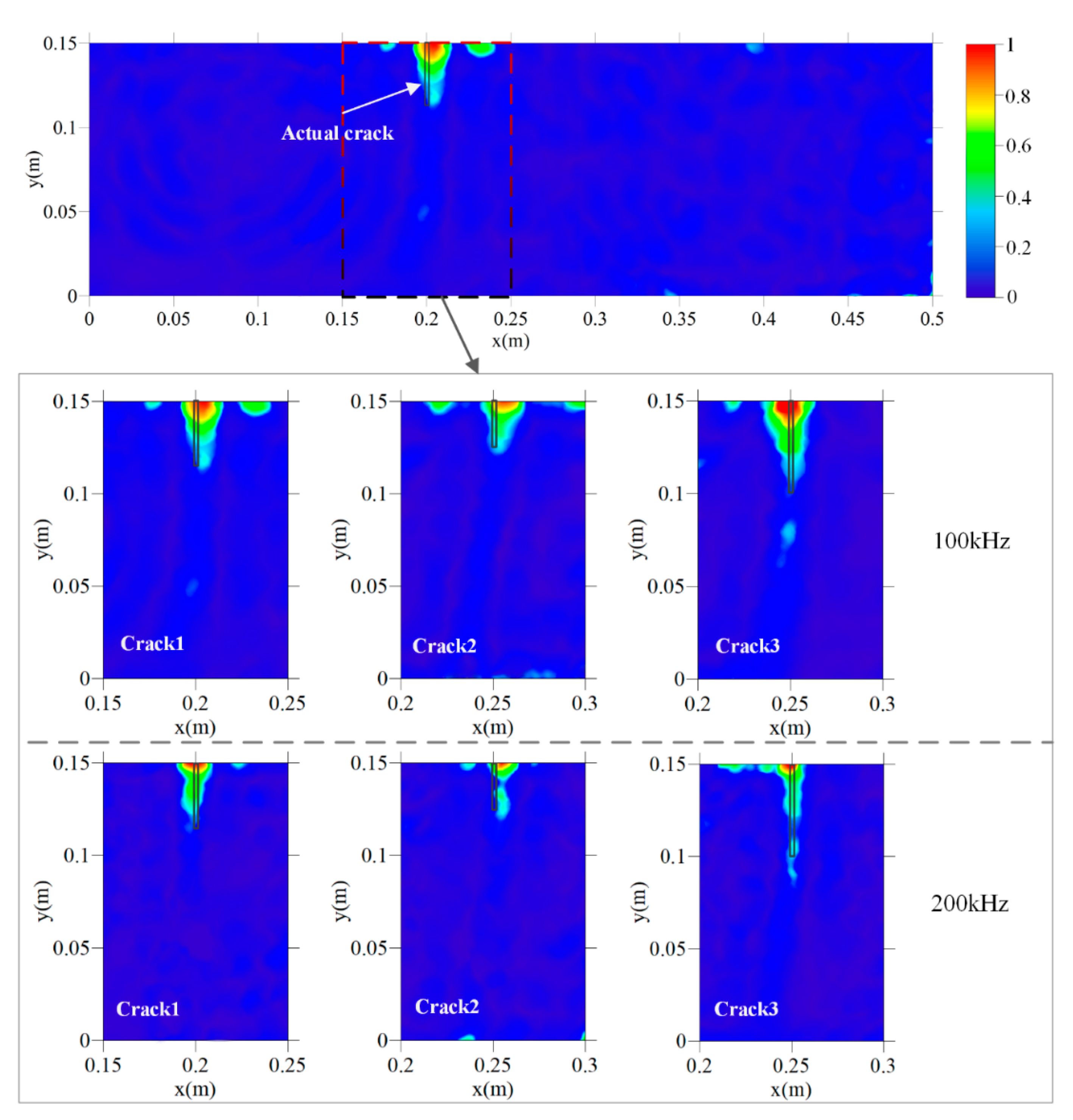
3.3.2. Inverse Simulation and Imaging Conditions
4. Experimental Study
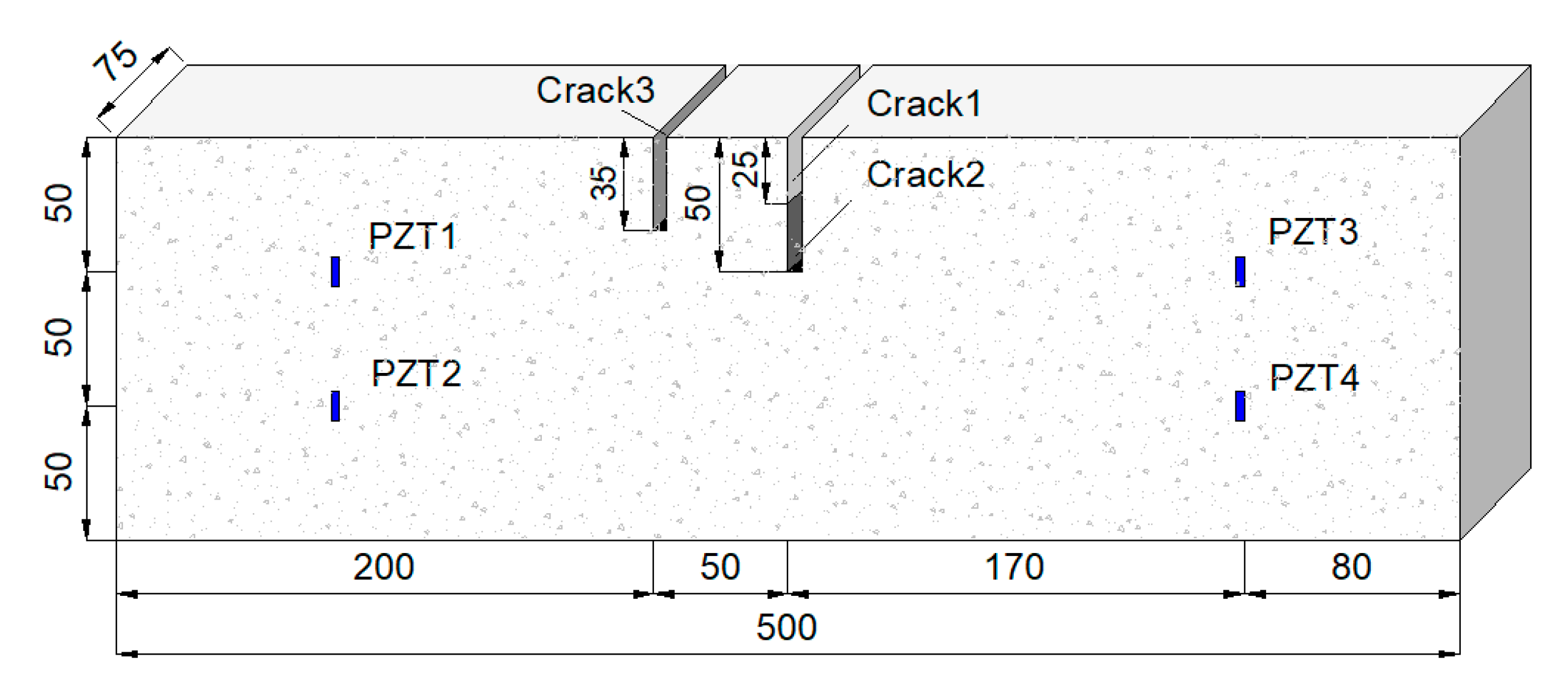
4.1. Experimental Setup
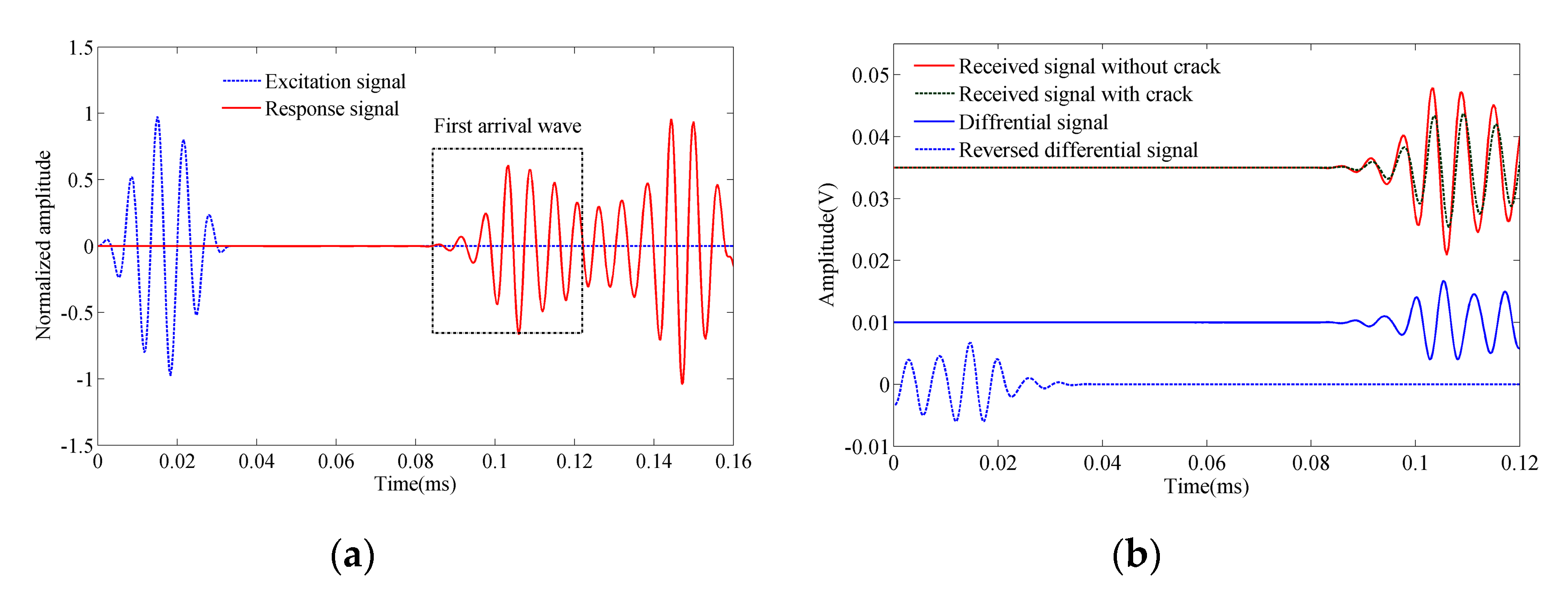
4.2. Experimental Procedures
4.3. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wu, Z.; Xu, B.; Gu, C.; Li, Z. Comprehensive evaluation methods for dam service status. Sci. China Ser. E Technol. Sci. 2012, 55, 2300–2312. [Google Scholar] [CrossRef]
- Wu, B.; Wu, Z.; Chen, B.; Su, H.; Bao, T.; Wang, S. Crack status analysis for concrete dams based on measured entropy. Sci. China Ser. E Technol. Sci. 2016, 59, 777–782. [Google Scholar] [CrossRef]
- Bouchette, G.; Church, P.; McFee, J.E.; Adler, A. Imaging of Compact Objects Buried in Underwater Sediments Using Electrical Impedance Tomography. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1407–1417. [Google Scholar] [CrossRef]
- Xiangan, W.; Xingxin, X.; Jin, W.; Dong, L.; Qizhen, R.; Shunming, H.; Jinyin, S. Research on the GPR exploration for various hidden dangers in water conservancy projects. Geol Prospect 1998, 3, 47–51. (In Chinese) [Google Scholar]
- Sevim, B.; Altunişik, A.C.; Bayraktar, A. Experimental evaluation of crack effects on the dynamic characteristics of a prototype arch dam using ambient vibration tests. Comput. Concr. 2012, 10, 277–294. [Google Scholar] [CrossRef]
- Sevim, B.; Altunisik, A.C.; Bayraktar, A. Structural identification of concrete arch dams by ambient vibration tests. Adv. Concr. Constr. 2013, 1, 227–237. [Google Scholar] [CrossRef]
- Abbas, M.; Shafiee, M. Structural Health Monitoring (SHM) and Determination of Surface Defects in Large Metallic Structures using Ultrasonic Guided Waves. Sensors 2018, 18, 3958. [Google Scholar] [CrossRef]
- Lad, D.B.; Faroz, S.A.; Ghosh, S. Fusion of Rebound Number and Ultrasonic Pulse Velocity Data for Evaluating the Concrete Strength Using Bayesian Updating. In Reliability, Safety and Hazard Assessment for Risk-Based Technologies; Springer: Singapore, 2020; pp. 437–448. [Google Scholar]
- Determining Crack Depth and Measurement Errors Using Time-of-Flight Diffraction Techniques. ACI Mater. J. 1999, 96, 190–195. [CrossRef]
- Hévin, G.; Abraham, O.; Pedersen, H.; Campillo, M. Characterization of surface cracks with Rayleigh waves: A numerical model. NDT E Int. 1998, 31, 289–297. [Google Scholar] [CrossRef]
- Crack Depth Estimation in Concrete Using Energy Transmission of Surface Waves. ACI Mater. J. 2008, 105, 510. [CrossRef][Green Version]
- Seher, M.; In, C.-W.; Kim, J.-Y.; Kurtis, K.E.; Jacobs, L.J. Numerical and Experimental Study of Crack Depth Measurement in Concrete Using Diffuse Ultrasound. J. Nondestruct. Eval. 2012, 32, 81–92. [Google Scholar] [CrossRef]
- Tian, H.; Xin, C.; Zhang, K. The reliability analysis on single plane detecting of ultrasonic wave for the concrete structures crack depth. J. Lanzhou Univ. Technol. 2013, 39, 133–136. (In Chinese) [Google Scholar]
- National Standard of the People’s Republic of China. Calibration Specification for Concrete Crack Width and Depth Measuring Instruments, JJF 1334-2012. Available online: http://www.gbstandards.org/index/GB_standard_english.asp?id=65720&word=Flash%20setting%20admixtures%20for%20s (accessed on 19 December 2020).
- Zhao, X.; Qian, T.; Mei, G.; Kwan, C.; Zane, R.; Walsh, C.; Paing, T.; Popovic, Z. Active health monitoring of an aircraft wing with an embedderd piezoelectric sensor/actuator network: II. Wireless approaches. Smart Mater. Struct. 2007, 16, 1218–1225. [Google Scholar] [CrossRef]
- Zhang, N.; Su, H. Application assessments of concrete piezoelectric smart module in civil engineering. Smart Struct. Syst. 2017, 19, 499–512. [Google Scholar] [CrossRef]
- Neville, A.M. Properties of Concrete; Longman: London, UK, 1995. [Google Scholar]
- Kamada, T.; Fujita, T.; Hatayama, T.; Arikabe, T.; Murai, N.; Aizawa, S.; Tohyama, K. Active vibration control of frame structures with smart structures using piezoelectric actuators (Vibration control by control of bending moments of columns). Smart Mater. Struct. 1997, 6, 448–456. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, Y.; Lu, Y.; Dong, P.; Guo, B.; Ding, W.; Xing, F.; Liu, T.; Dong, B. In-situ crack propagation monitoring in mortar embedded with cement-based piezoelectric ceramic sensors. Constr. Build. Mater. 2016, 126, 361–368. [Google Scholar] [CrossRef]
- Gu, H.; Song, G.; Dhonde, H.; Mo, Y.L.; Yan, S. Concrete early-age strength monitoring using embedded piezoelectric transducers. Smart Mater. Struct. 2006, 15, 1837–1845. [Google Scholar] [CrossRef]
- Song, G.; Olmi, C.; Gu, H. An overheight vehicle–bridge collision monitoring system using piezoelectric transducers. Smart Mater. Struct. 2007, 16, 462–468. [Google Scholar] [CrossRef]
- Su, H.; Zhang, N.; Li, H. Concrete piezoceramic smart module pairs-based damage diagnosis of hydraulic structure. Compos. Struct. 2018, 183, 582–593. [Google Scholar] [CrossRef]
- Zou, D.; Liu, T.; Huang, Y.; Zhang, F.; Du, C.; Li, B. Feasibility of water seepage monitoring in concrete with embedded smart aggregates by P-wave travel time measurement. Smart Mater. Struct. 2014, 23, 067003. [Google Scholar] [CrossRef]
- Feng, Q.; Kong, Q.; Huo, L.; Song, G. Crack detection and leakage monitoring on reinforced concrete pipe. Smart Mater. Struct. 2015, 24, 115020. [Google Scholar] [CrossRef]
- Baharom, S.; Mutlib, N.K.; El-Shafie, A. Crack detection of underwater concrete beams using ultrasonic surface waves. In Proceedings of the Advances in Structural Engineering and Mechanics-ASEM15, Incheon, Korea, 25–29 August 2015. [Google Scholar]
- Marković, N.; Nestorović, T.; Stojić, D. Numerical modeling of damage detection in concrete beams using piezoelectric patches. Mech. Res. Commun. 2015, 64, 15–22. [Google Scholar] [CrossRef]
- Stojić, D.; Nestorović, T.; Marković, N.; Cvetković, R.; Stojić, N. Detection of damage to reinforced-concrete structures using piezoelectric intelligent modules. Građevinar 2016, 68, 371–380. [Google Scholar]
- Fink, M. Time reversal of ultrasonic fields. I. Basic principles. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 555–566. [Google Scholar] [CrossRef] [PubMed]
- Kerbrat, E.; Prada, C.; Cassereau, D.; Fink, M. Ultrasonic nondestructive testing of scattering media using the decomposition of the time-reversal operator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2002, 49, 1103–1113. [Google Scholar] [CrossRef]
- Song, H.-C. An Overview of Underwater Time-Reversal Communication. IEEE J. Ocean. Eng. 2016, 41, 644–655. [Google Scholar] [CrossRef]
- Fink, M.; Montaldo, G.; Tanter, M. Time-Reversal Acoustics in Biomedical Engineering. Annu. Rev. Biomed. Eng. 2003, 5, 465–497. [Google Scholar] [CrossRef]
- Xiaobin, H.; Jianxi, Z.; Peisong, L.; Guojian, H.; Zhou, J.; Lin, P.; Huang, G.; Hong, X.-B. An imaging method for the covered damage region of strand wire based on dual time reversal using piezoceramic transducers. Smart Mater. Struct. 2017, 26, 104005. [Google Scholar] [CrossRef]
- Derode, A.; Tourin, A.; Fink, M. Time reversal in multiply scattering media. Ultrasonics 1998, 36, 443–447. [Google Scholar] [CrossRef]
- Ulrich, T.J.; Johnson, P.A.; Guyer, R.A. Interaction Dynamics of Elastic Waves with a Complex Nonlinear Scatterer through the Use of a Time Reversal Mirror. Phys. Rev. Lett. 2007, 98, 104301. [Google Scholar] [CrossRef]
- Payan, C.; Ulrich, T.J.; Le Bas, P.-Y.; Saleh, T.; Guimarães, M. Probing materials damage at various depths by use of Time Reversal Elastic Nonlinearity Diagnostic: Application to concrete. In Proceedings of the XVII International Conference on Nonlinear Elasticity in Materials; Acoustical Society of America (ASA), Cefalu, Italy, 1–7 June 2012; Volume 16, p. 45013. [Google Scholar]
- Kocur, G.K.; Saenger, E.H.; Grosse, C.U.; Vogel, T. Time reverse modeling of acoustic emissions in a reinforced concrete beam. Ultrasonics 2016, 65, 96–104. [Google Scholar] [CrossRef] [PubMed]
- Gao, W.; Li, H.; Ho, S.C.M. A Novel Embeddable Tubular Piezoceramics-Based Intelligent module for Damage Detection in Two-Dimensional Concrete Structures. Sensors 2019, 19, 1501. [Google Scholar] [CrossRef] [PubMed]
- Tanter, M.; Thomas, J.-L.; Fink, M. Time reversal and the inverse filter. J. Acoust. Soc. Am. 2000, 108, 223–234. [Google Scholar] [CrossRef]
- Joshi, S.P. Non-linear constitutive relations for piezoceramic materials. Smart Mater. Struct. 1992, 1, 80–83. [Google Scholar] [CrossRef]
- Wang, Z.; Kwan, A.; Chan, H. Mesoscopic study of concrete I: Generation of random aggregate structure and finite element mesh. Comput. Struct. 1999, 70, 533–544. [Google Scholar] [CrossRef]
- Zhou, W. Fundamental Study on Smart Piezoelectric Monitoring Technique Applied to Concrete Structure. Master’s Thesis, Chongqing University, Chongqing, China, 2003. [Google Scholar]






| Mortar | Aggregate | Piezoelectric Patch | |
|---|---|---|---|
| Young’s modulus (GPa) | 30 | 80 | 75 |
| Poisson’s ratio | 0.2 | 0.2 | 0.32 |
| Density (kg/m3) | 2400 | 2800 | 7500 |
| Crack 1 | Crack 2 | Crack 3 | |
|---|---|---|---|
| Crack length (mm) | 25 | 50 | 35 |
| Distance to the left side (mm) | 250 | 250 | 200 |
| Crack Opening Position | Crack Size | |||||
|---|---|---|---|---|---|---|
| FE Modeling | Distance to the Left Side (mm) | Error (mm) | Vertical Depth (mm) | Error (mm) | Relative Error (%) | RMSD |
| Crack 1 | 201 | 1 | 381 | 31 | 8.9 | 0.3472 |
| Crack 2 | 248 | −2 | 272 | 22 | 8.7 | 0.2398 |
| Crack 3 | 249 | −1 | 689 | 189 | 37.8 | 0.5288 |
| Experiment | ||||||
| Crack 1 | 203 | 3 | 389 | 39 | 11.2 | 0.2961 |
| Crack 2 | 246 | −4 | 257 | 7 | 3.1 | 0.2168 |
| Crack 3 | 239 | −11 | 447 | 53 | 10.4 | 0.3834 |
| Crack Opening Position | Crack Size | |||||
|---|---|---|---|---|---|---|
| 100 kHz | Distance to the Left Side (mm) | Error (mm) | Vertical Depth (mm) | Error (mm) | Relative Error (%) | |
| Crack 1 | 204 | 4 | 371 | 21 | 6 | |
| Crack 2 | 256 | 6 | 284 | 34 | 13.6 | |
| Crack 3 | 249 | −1 | 693 | 193 | 38.6 | |
| 200 kHz | ||||||
| Crack 1 | 200 | 0 | 366 | 16 | 4.6 | |
| Crack 2 | 255 | 5 | 297 | 47 | 18.8 | |
| Crack 3 | 249 | −1 | 621 | 121 | 24.2 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, J.; Chen, B.; Shao, C.; Li, J.; Wu, B. Time Reverse Modeling of Damage Detection in Underwater Concrete Beams Using Piezoelectric Intelligent Modules. Sensors 2020, 20, 7318. https://doi.org/10.3390/s20247318
Liang J, Chen B, Shao C, Li J, Wu B. Time Reverse Modeling of Damage Detection in Underwater Concrete Beams Using Piezoelectric Intelligent Modules. Sensors. 2020; 20(24):7318. https://doi.org/10.3390/s20247318
Chicago/Turabian StyleLiang, Jiachen, Bo Chen, Chenfei Shao, Jianming Li, and Bangbin Wu. 2020. "Time Reverse Modeling of Damage Detection in Underwater Concrete Beams Using Piezoelectric Intelligent Modules" Sensors 20, no. 24: 7318. https://doi.org/10.3390/s20247318
APA StyleLiang, J., Chen, B., Shao, C., Li, J., & Wu, B. (2020). Time Reverse Modeling of Damage Detection in Underwater Concrete Beams Using Piezoelectric Intelligent Modules. Sensors, 20(24), 7318. https://doi.org/10.3390/s20247318






