Experimental Demonstration of Ship Target Detection in GNSS-Based Passive Radar Combining Target Motion Compensation and Track-before-Detect Strategies
Abstract
:1. Introduction
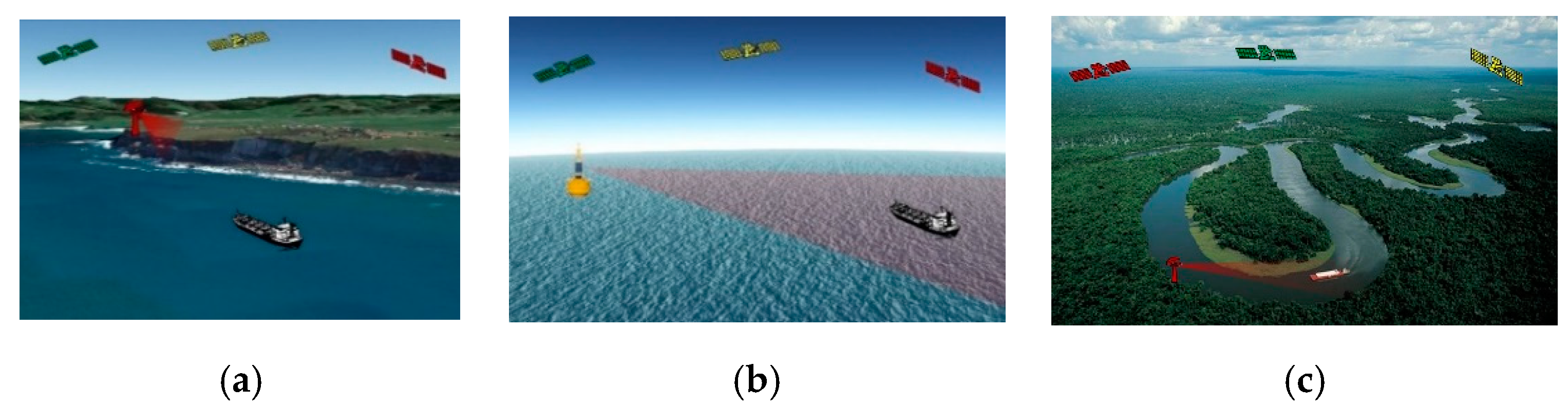
2. GNSS-Based Passive Radar for Maritime Surveillance
3. Detection Strategy
3.1. Target Motion Compensation Technique
- -
- Doppler migration compensation—the assumed motion model entails a linear variation of the target Doppler (5), therefore the frame to frame Doppler migration is given by . Moreover, Doppler migration can occur even inside the individual frame and it can be described by the law , being the slow time variable spanning the individual frame. Therefore, both the Doppler migration inside each frame and frame to frame are both related to . These can be compensated by applying a slow time phase ramp comprising both sources of migration.
- -
- Range migration compensation—this step is fed by the data in the fast-frequency and Doppler domain. Therefore, after the Doppler migration compensation, a slow time FFT and a fast time FFT are implemented. While range migration inside each frame can be neglected due to the coarse range resolution (not higher than 15 m for the GNSS signals with largest bandwidth, e.g., Galileo E5a/b or GPS L5), the frame to frame migration must be compensated. Form (4), the frame-to-frame range migration is composed by a range walk and a range curvature component, respectively described as and . The term depends on the Doppler position and therefore it can be adaptively compensated by applying a fast frequency phase ramp for each Doppler bin, while can be compensated by using a phase ramp according to .
- -
- Motion-compensated RD map formation—a fast time inverse FFT allows finally achieving the motion compensated RD map.
- (i)
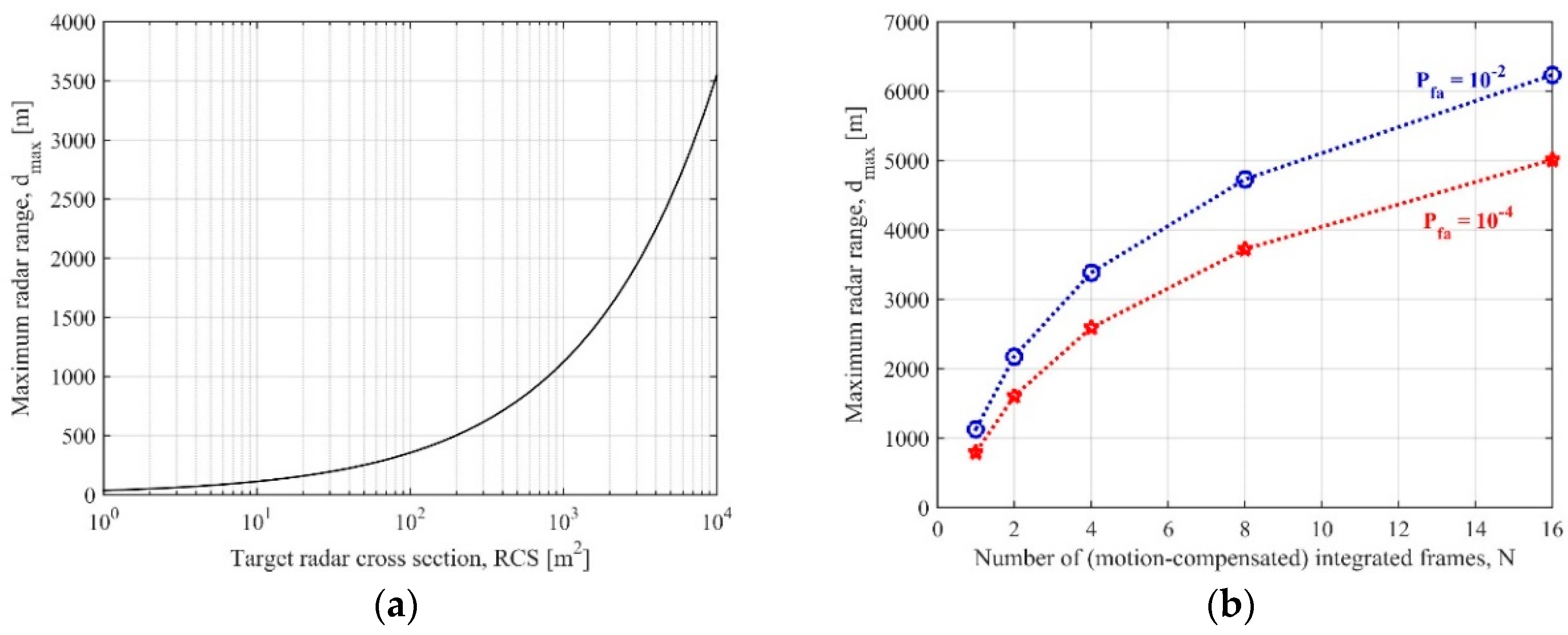
- As the procedure is based on a modelling of the motion, the performance can degrade in the case of model mismatches. Moreover, the model implicitly assumes the target as point-like. It should be noted that the sizes of ship targets of interest could be greater than the range resolution cell and that, depending on the particular motion conditions, the target energy could spread over multiple Doppler cells [31]. Because of the temporal variation of the target electro-magnetic response, it cannot be guaranteed that the strongest scattering point is confined to the same resolution cell in the motion-compensated maps pertaining the different frames. As the multi-frame integration is performed on a pixel basis, the highest integration gain could not be reached.
- (ii)
- For given bounds of the Doppler rate to test, the sampling rule (6) implies that the number of filters in the bank increases with the number of integrated frames, entailing a direct increase of the computational load.
3.2. Track-before-Detect Processor
3.2.1. Track Formation
3.2.2. Track Pruning
3.2.3. Track Confirmation
- (1)
- It could be noticed that the kinematic rules for plots correlation are still based on a linear Doppler model, as in the TMC. However, this model has to hold only inside each scan, while the technique allows to integrate returns from plots having different Doppler rates (because of (11) and as depicted in Figure 5). This allows a higher degree of freedom in performing energy integration among the overall observation interval.
- (2)
- The integration is no more constrained by the resolution cells, as the TBD processor links plots having the highest intensity within an admissible RD area.
- (3)
- The inclusion of proper margins in range and Doppler further relaxes the impositions on the target kinematics, so that the processor can handle deviations between the theoretical and actual motion model, including the presence of multiple scattering centers in the case of extended targets.
4. Experimental Verification
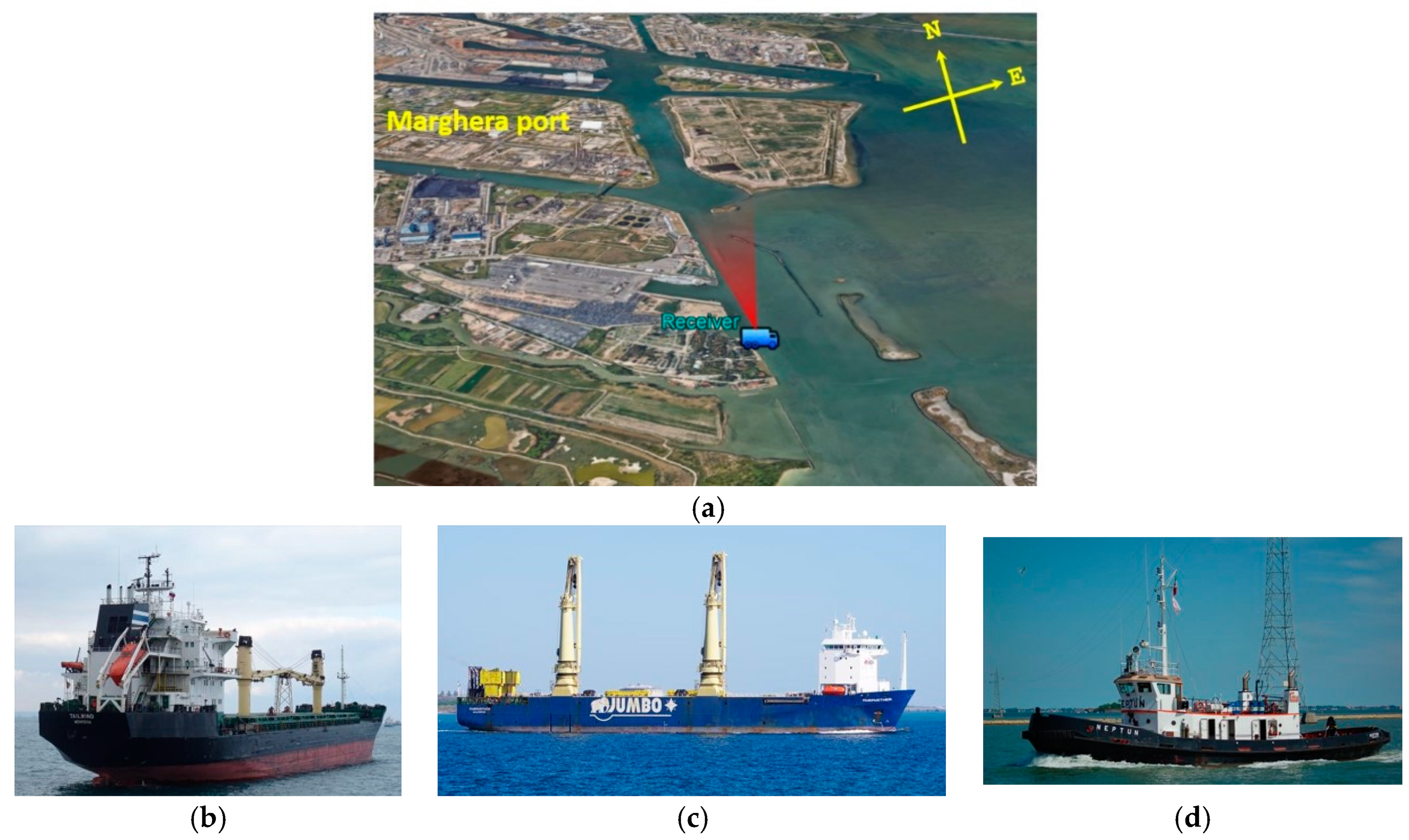
4.1. Scenario 1: Port Operations
- -
- Fairpartner has been correctly detected in almost all the epochs in which it was in the FOV for all the considered . This is not an unexpected result, as this is a massive target very close to the receiver so that it has a high detection probability even for low . However, even if small, an increase of the detection rate could be shown lowering the threshold: In the 22 timestamps in which it was in the FOV, it has been detected 20, 21 and 22 times for equal to 10−4, 10−3, and 10−2, respectively.
- -
- The use of the lower threshold allowed detecting Tailwind (which is at a higher distance than Fairpartner) for a longer interval, as it can be easily observed by comparing the tracklets in Figure 7b,d,f. Particularly, it was detected at longer ranges with = 10−2 and evaluating the detection rate as the number of scans in which it gave rise to a confirmed detection over the overall scans, we move from 33% and 58% for = 10−4, 10−3, respectively, up to 89% when = 10−2.
- -
- Neptun is a small target, which has small chances to be detected. In fact, with conventional processing involving values equal to 10−3 and 10−4, it has not been detected. Nevertheless, using the proposed approach with a lower detection threshold ( equal to 10−2), it was nicely detected.
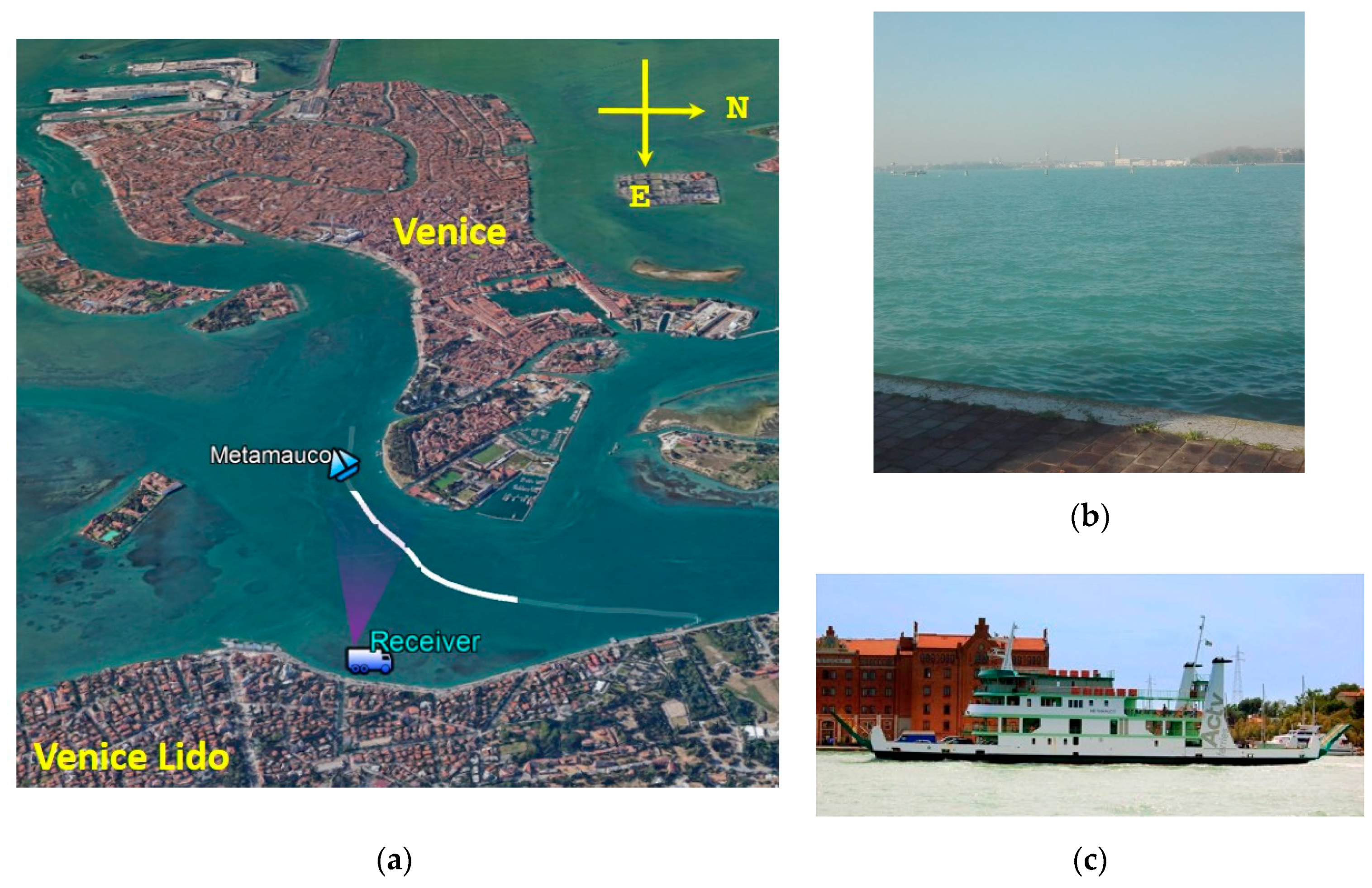
4.2. Scenario 2: Navigation in Open Area
4.3. Scenario 3: River Shipping
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Griffiths, H.D.; Baker, C.J. Passive coherent location radar systems. Part 1: Performance prediction. IEE Proc. Radar Sonar Navig. 2005, 152, 153–159. [Google Scholar] [CrossRef]
- Colone, F.; Bongioanni, C.; Lombardo, P. Multifrequency integration in FM radio-based passive bistatic radar. Part I: Target detection. IEEE Aerosp. Electron. Syst. Mag. 2013, 28, 28–39. [Google Scholar] [CrossRef]
- Krysik, P.; Samczynski, P.; Malanowski, M.; Maslikowski, L.; Kulpa, K.S. Velocity measurement and traffic monitoring using a GSM passive radar demonstrator. IEEE Aerosp. Electron. Syst. Mag 2012, 27, 43–51. [Google Scholar] [CrossRef]
- Pastina, D.; Colone, F.; Martelli, T.; Falcone, P. Parasitic exploitation of Wi-Fi signals for indoor radar surveillance. IEEE Trans. Veh. Technol. 2015, 64, 1401–1415. [Google Scholar] [CrossRef]
- Cristallini, D.; Caruso, M.; Falcone, P.; Langellotti, D.; Bongioanni, C.; Colone, F.; Scafè, S.; Lombardo, P. Space-Based Passive Radar Enabled by the New Generation of Geostationary Broadcast Satellites. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2010; pp. 1–11. [Google Scholar]
- Barott, W.C.; Butka, B. A passive bistatic radar for detection of aircraft using spaceborne transmitters. In Proceedings of the IEEE/AIAA 30th Digital Avionics System Conference, Seattle, WA, USA, 16–20 October 2011; pp. 1A2-1–1A2-11. [Google Scholar]
- Zhang, Q.; Antoniou, M.; Chang, W.; Cherniakov, M. Spatial decorrelation in GNSS-based SAR coherent change detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 219–228. [Google Scholar] [CrossRef]
- Ma, H.; Antoniou, M.; Cherniakov, M. Passive GNSS-based SAR resolution improvement using joint Galileo E5 signals. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1640–1644. [Google Scholar] [CrossRef]
- Bárcena-Humanes, J.L.; Gómez-del-Hoyo, P.J.; Jarabo-Amores, M.P.; Mata-Moya, D.; Rosado-Sanz, J. On the potentials of satellite based passive radars for smart sensors networks in smart cities. In Proceedings of the IEEE 17th International Conference on Ubiquitous Wireless Broadband (ICUWB), Salamanca, Spain, 12–15 September 2017; pp. 1–5. [Google Scholar]
- Brisken, S.; Moscardelli, M.; Seidel, V.; Schwark, C. Passive radar imaging using DVB-S2. In Proceedings of the IEEE Radar Conference, Seattle, WA, USA, 8–12 May 2017; pp. 552–556. [Google Scholar]
- Li, Z.; Santi, F.; Pastina, D.; Lombardo, P. Multi-frame fractional Fourier transform technique for moving target detection with space-based passive radar. IET Radar Sonar Navig. 2017, 11, 822–828. [Google Scholar] [CrossRef]
- Sayin, A.; Cherniakov, M.; Antoniou, M. Passive radar using Starlink transmissions: A theoretical study. In Proceedings of the 20th International Radar Symposium (IRS), Ulm, Germany, 26–28 June 2019; pp. 1–7. [Google Scholar]
- Golabi, M.; Sheikhi, A.; Biguesh, M. A new approach for sea target detection in satellite based passive radar. In Proceedings of the Iranian Conference Electrical Engineering (ICEE), Mashhad, Iran, 14–16 May 2013; pp. 1–5. [Google Scholar]
- Stove, A.G.; Gashinova, M.; Hristov, S.; Cherniakov, M. Passive maritime surveillance using satellite communication signals. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 2987–2997. [Google Scholar] [CrossRef]
- Pisciottano, I.; Cristallini, D.; Pastina, D. Maritime target imaging via simultaneous DVB-T and DVB-S passive ISAR. IET Radar Sonar Navig. 2019, 13, 1479–1487. [Google Scholar] [CrossRef]
- Ma, H.; Antoniou, M.; Pastina, D.; Santi, F.; Pieralice, F.; Bucciarelli, M.; Cherniakov, M. Maritime moving target indication using passive GNSS-based bistatic radar. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 115–130. [Google Scholar] [CrossRef]
- Pastina, D.; Santi, F.; Pieralice, F.; Bucciarelli, M.; Ma, H.; Tzagkas, D.; Antoniou, M.; Cherniakov, M. Maritime moving target long time integration for GNSS-based passive bistatic radar. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 3060–3083. [Google Scholar] [CrossRef] [Green Version]
- Ma, H.; Antoniou, M.; Stove, A.G.; Winkel, J.; Cherniakov, M. Maritime moving target localization using passive GNSS-based multistatic radar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4808–4819. [Google Scholar] [CrossRef]
- Santi, F.; Pieralice, F.; Pastina, D. Joint detection and localization of vessels at sea with a GNSS-based multistatic radar. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5894–5913. [Google Scholar] [CrossRef]
- Chen, X.; Guan, J.; Liu, N.; He, Y. Maneuvering Target Detection via Radon-Fractional Fourier Transform-Based Long-Time Coherent Integration. IEEE Trans. Signal. Process. 2014, 62, 939–953. [Google Scholar] [CrossRef]
- Barniv, Y. Dynamic programming solution for detecting dim moving target. IEEE Trans. Aerosp. Electron. Syst. 1985, 21, 144–156. [Google Scholar] [CrossRef]
- Buzzi, S.; Lops, M.; Venturino, L. Track-before-detect procedures for early detection of moving target from airborne radars. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 937–954. [Google Scholar] [CrossRef]
- Orlando, D.; Venturino, L.; Lops, M.; Ricci, G. Track-before-detect strategies for STAP radars. IEEE Trans. Signal Process. 2010, 58, 933–938. [Google Scholar] [CrossRef]
- Chan, Y.T.; Niezgoda, G.H.; Morton, S.P. Passive sonar detection and localization by matched velocity filtering. IEEE J. Ocean. Eng. 1995, 20, 179–189. [Google Scholar] [CrossRef]
- Lehmann, F. Recursive Bayesian Filtering for Multitarget Track-Before-Detect in Passive Radars. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2458–2480. [Google Scholar] [CrossRef]
- Davey, S.J.; Rutten, M.G.; Cheung, B. A comparison of detection performance for several track-before-detect algorithms. In Proceedings of the 11th International Conference Information Fusion, Cologne, Germany, 30 June–3 July 2008; pp. 1–8. [Google Scholar]
- Grossi, E.; Lops, M.; Venturino, L. A novel dynamic-programming algorithm for track-before-detect in radar systems. IEEE Trans. Signal Process. 2013, 61, 2608–2619. [Google Scholar] [CrossRef]
- Aprile, A.; Grossi, E.; Lops, M.; Venturino, L. Track-before-detect for sea clutter rejection: Tests with real data. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1035–1045. [Google Scholar] [CrossRef]
- Santi, F.; Pastina, D. Application of track-before-detect techniques in GNSS-based passive radar for maritime surveillance. In Proceedings of the IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar]
- Galileo open service-signal. In Space Interface Control Document (OS SIS ICD); European Space Agency/European GNSS Supervisory Authority: Prague, Czech Republic, 2015.
- Santi, F.; Pieralice, F.; Pastina, D.; Antoniou, M.; Cherniakov, M. Passive radar imagery of ship targets by using navigation satellites transmitters of opportunity. In Proceedings of the 20th International Radar Symposium (IRS), Ulm, Germany, 26–28 June 2019; pp. 1–10. [Google Scholar]
- Grossi, E.; Lops, M.; Venturino, L. A track-before-detect algorithm with thresholded observations and closely-spaced targets. IEEE Signal Process. Lett. 2013, 20, 1171–1174. [Google Scholar] [CrossRef]
- Grossi, E.; Lops, M.; Venturino, L. A heuristic algorithm for track-before-detect with thresholded observations in radar systems. IEEE Signal Process. Lett. 2013, 20, 811–814. [Google Scholar] [CrossRef]
- Marine Traffic. Available online: https://www.marinetraffic.com/ (accessed on 2 October 2019).
- Malanowski, M.; Kulpa, K.; Suchozebrski, R. Two-stage tracking algorithm for passive radar. In Proceedings of the 12th International Conference on Information Fusion, Seattle, WA, USA, 6–9 July 2009; pp. 1800–1806. [Google Scholar]







| Parameter | Symbol | Value |
|---|---|---|
| Power density on the ground | 3 × 10−14 W/m2 | |
| Antenna gain | 15 dB | |
| Noise figure | 1.5 dB | |
| Losses | 2 dB | |
| Noise Temperature | 290 K | |
| Boltzmann constant | 1.38 × 10−23 J/K |
| Parameter | Value | |
|---|---|---|
| Satellite | Number | GSAT0208 |
| PRN code | E08 | |
| Aspect angle (clockwise from North) | 100° | |
| Elevation angle | 57° | |
| Signal processing | Frame duration Tf | 2.5 s |
| Number of integrated frames N | 4 | |
| Number of scans for plot confirmation L | 8 | |
| Offset between consecutive scans ΔT | 5 s | |
| Maximum consecutive missed detection P | 3 | |
| Minimum detections in a track Q | 5 | |
| Parameter | Value | |
|---|---|---|
| Satellite | Number | GSAT02014 |
| PRN code | E05 | |
| Aspect angle (clockwise from North) | 80° | |
| Elevation angle | 55° | |
| Signal processing | Frame duration Tf | 3 s |
| Number of integrated frames N | 3 | |
| Number of scans for plot confirmation L | 8 | |
| Offset between consecutive scans ΔT | 4.5 s | |
| Maximum consecutive missed detection P | 3 | |
| Minimum detections in a track Q | 5 | |
| Parameter | Value | |
|---|---|---|
| Satellite 1 | Number | GSAT02010 |
| PRN code | E01 | |
| Aspect angle (clockwise from North) | 164° | |
| Elevation angle | 9° | |
| Satellite 2 | Number | GSAT02014 |
| PRN code | E05 | |
| Aspect angle (clockwise from North) | −116° | |
| Elevation angle | 36° | |
| Signal processing | Frame duration Tf | 2.5 s |
| Number of integrated frames N | 4 | |
| Number of scans for plot confirmation L | 8 | |
| Offset between consecutive scans ΔT | 5 s | |
| Maximum consecutive missed detection P | 3 | |
| Minimum detections in a track Q | 5 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santi, F.; Pastina, D.; Bucciarelli, M. Experimental Demonstration of Ship Target Detection in GNSS-Based Passive Radar Combining Target Motion Compensation and Track-before-Detect Strategies. Sensors 2020, 20, 599. https://doi.org/10.3390/s20030599
Santi F, Pastina D, Bucciarelli M. Experimental Demonstration of Ship Target Detection in GNSS-Based Passive Radar Combining Target Motion Compensation and Track-before-Detect Strategies. Sensors. 2020; 20(3):599. https://doi.org/10.3390/s20030599
Chicago/Turabian StyleSanti, Fabrizio, Debora Pastina, and Marta Bucciarelli. 2020. "Experimental Demonstration of Ship Target Detection in GNSS-Based Passive Radar Combining Target Motion Compensation and Track-before-Detect Strategies" Sensors 20, no. 3: 599. https://doi.org/10.3390/s20030599
APA StyleSanti, F., Pastina, D., & Bucciarelli, M. (2020). Experimental Demonstration of Ship Target Detection in GNSS-Based Passive Radar Combining Target Motion Compensation and Track-before-Detect Strategies. Sensors, 20(3), 599. https://doi.org/10.3390/s20030599





