Simulation-Based Design and Optimization of Rectangular Micro-Cantilever-Based Aerosols Mass Sensor
Abstract
:1. Introduction
2. Materials and Methods
2.1. Principle of the MCL-Based Mass Sensors
2.2. Theory
2.3. Design
2.3.1. The Shapes of MCLs
2.3.2. The Slots of MCLs
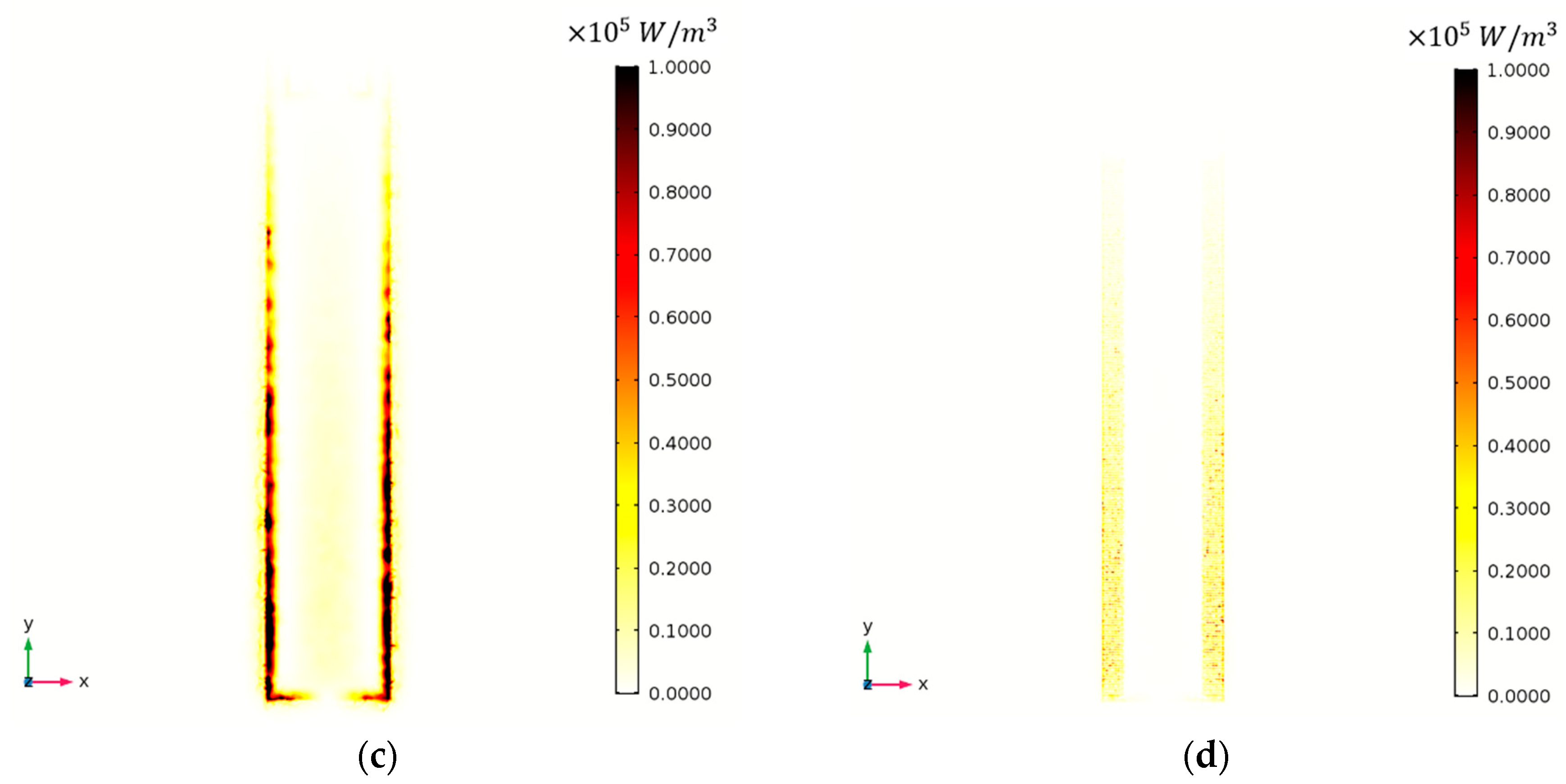
2.3.3. The Edge Serrations of MCLs
2.3.4. Material Property of Air
2.4. Modeling and Validation
3. Results and Discussion
3.1. Simulation-Model Validation
3.2. The Effects of MCLs’ Shapes
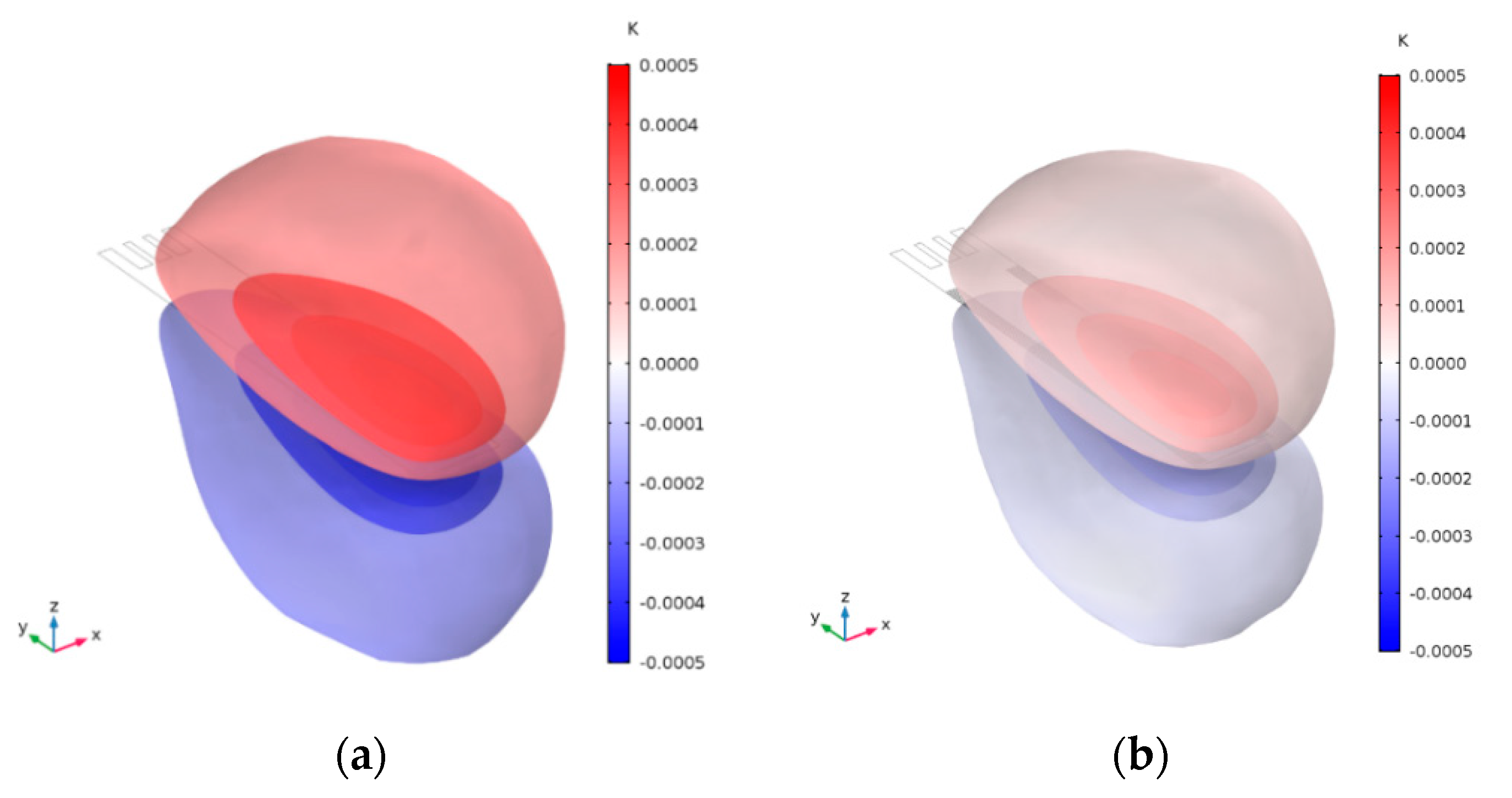
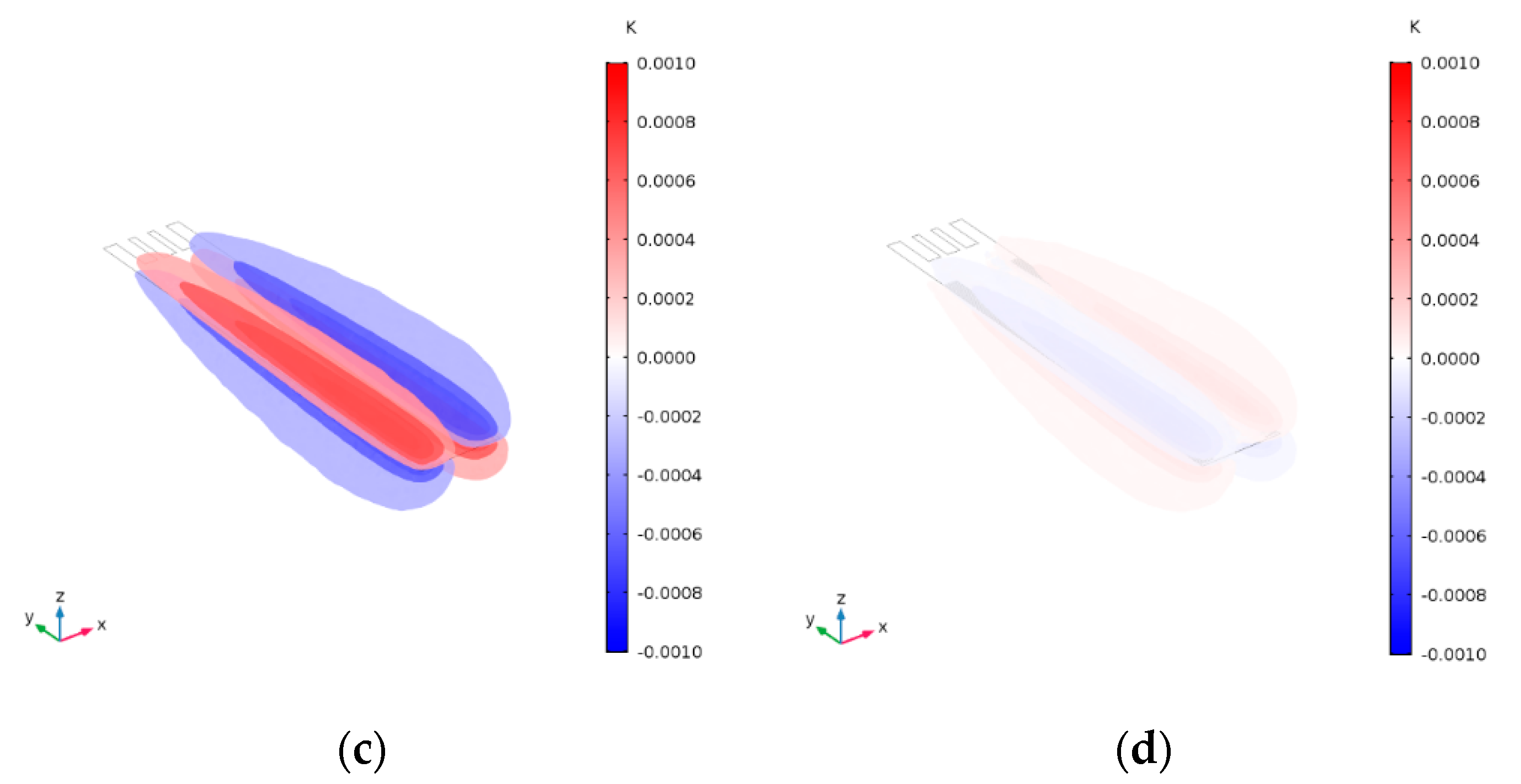
3.2.1. The Vibration Mode
3.2.2. The Detection Performance
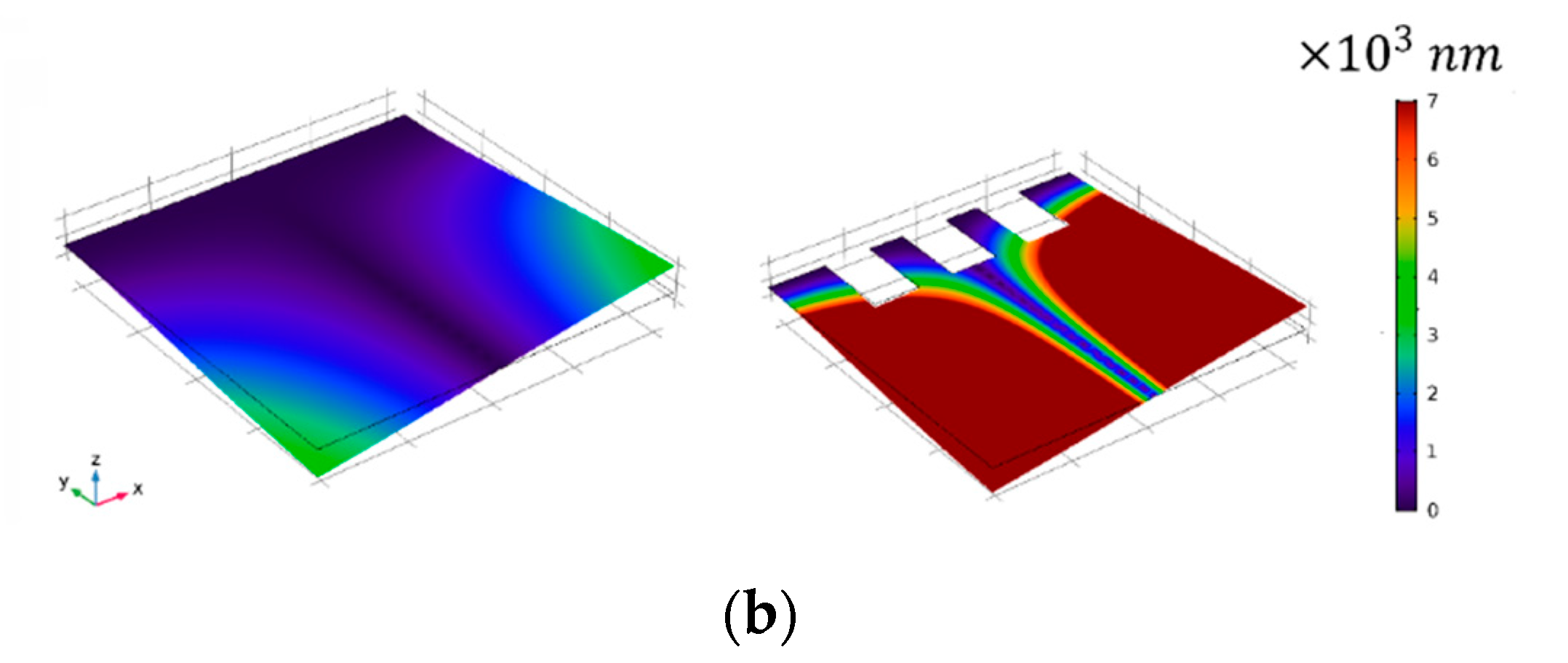
3.3. Effect of MCL Slots
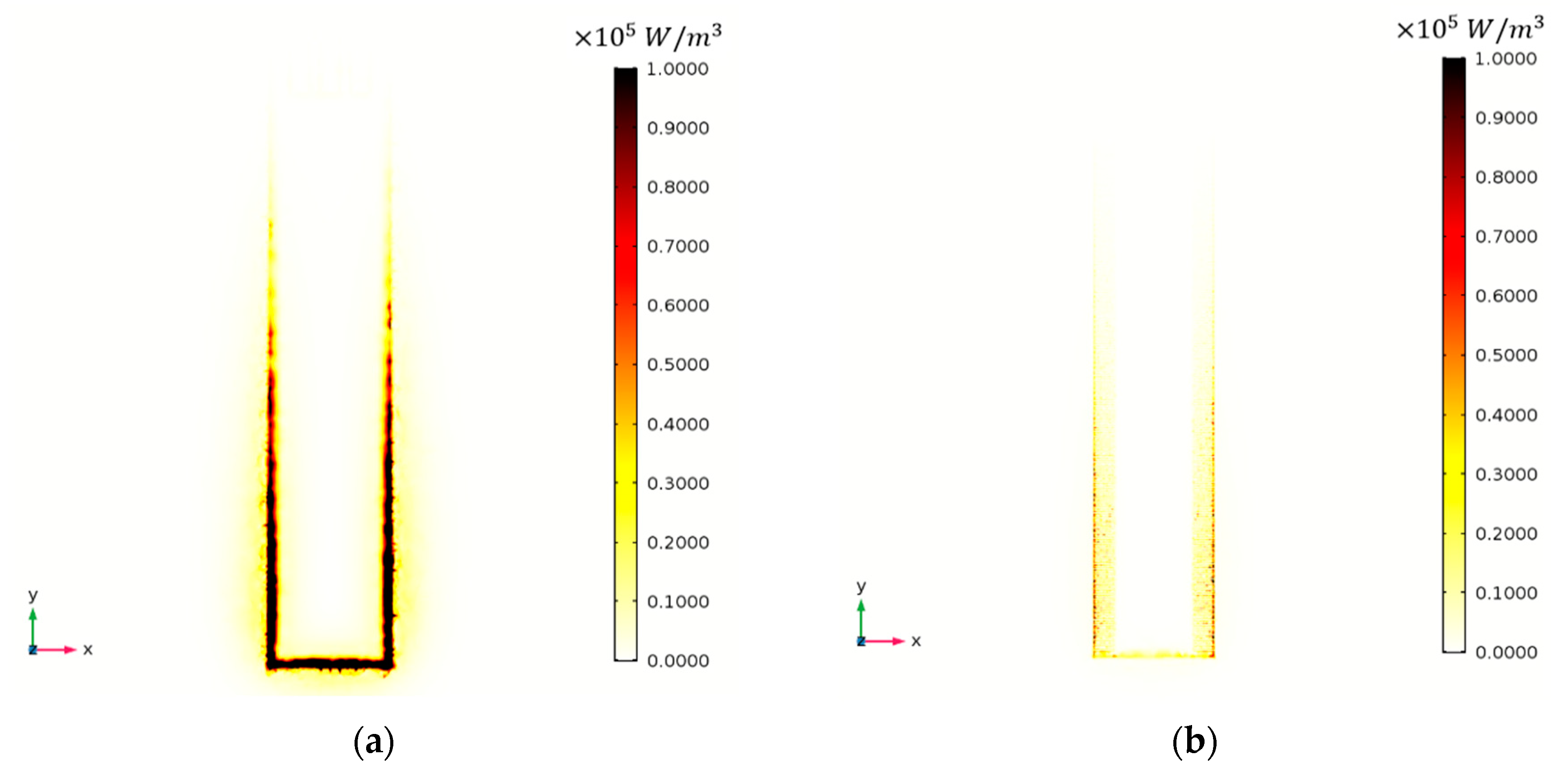
3.4. Effect of Edge Serration
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Soysal, U.; Géhin, E.; Algré, E.; Berthelot, B.; Da, G.; Robine, E. Aerosol mass concentration measurements: Recent advancements of real-time nano/micro systems. J. Aerosol Sci. 2017, 114, 42–54. [Google Scholar] [CrossRef]
- Chueinta, W.; Hopke, P.K. Beta Gauge for Aerosol Mass Measurement. Aerosol Sci. Technol. 2001, 35, 840–843. [Google Scholar] [CrossRef]
- Zhu, K.; Zhang, J.J.; Lioy, P.J. Evaluation and Comparison of Continuous Fine Particulate Matter Monitors for Measurement of Ambient Aerosols. J. Air Waste Manag. Assoc. 2007, 57, 1499–1506. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Favez, O.; Cachier, H.; Sciare, J.; Le Moullec, Y. Characterization and contribution to PM 2.5 of semi-volatile aerosols in Paris (France). Atmos. Environ. 2007, 41, 7969–7976. [Google Scholar] [CrossRef]
- Grover, B.D. Measurement of total PM 2.5 mass (nonvolatile plus semivolatile) with the Filter Dynamic Measurement System tapered element oscillating microbalance monitor. J. Geophys. Res. 2005, 110, 1–9. [Google Scholar] [CrossRef]
- Jianwen, S.; Kun, Y.; Zewen, L.; Yanwu, L. A system of continuous particles monitoring using virtual impactor. In Proceedings of the 2015 12th IEEE International Conference on Electronic Measurement & Instruments (ICEMI), Qingdao, China, 16–18 July 2015; pp. 1216–1220. [Google Scholar]
- Shendrikar, A.D.; Steinmetz, W.K. Integrating nephelometer measurements for the airborne fine particulate matter (PM 2.5) mass concentrations. Atmos. Environ. 2003, 37, 1383–1392. [Google Scholar] [CrossRef]
- Hao, Z.; Abdolvand, R.; Ayazi, F. A High-Q Length-Extensional Bulk-Modemass Sensor with Annexed Sensing Platforms. In Proceedings of the 19th IEEE International Conference on Micro Electro Mechanical Systems, Istanbul, Turkey, 22–26 January 2006; pp. 598–601. [Google Scholar]
- Lee, J.E.; Zhu, Y.; Seshia, A.A. A bulk acoustic mode single-crystal silicon microresonator with a high-quality factor. J. Micromech. Microeng. 2008, 18, 064001. [Google Scholar] [CrossRef] [Green Version]
- Natalia, N.; Gfeller, K.Y.; Natalia, B.; Marcel, D.; Peter, L.H.; Hans-Joachim, G.; Martin, H. An antibody-sensitized microfabricated cantilever for the growth detection of Aspergillus niger spores. Microsc. Microanal. 2007, 13, 13–17. [Google Scholar]
- Gupta, A.; Akin, D.; Bashir, R. Single virus particle mass detection using microresonators with nanoscale thickness. Appl. Phys. Lett. 2004, 84, 1976–1978. [Google Scholar] [CrossRef]
- Davila, A.P.; Jang, J.; Gupta, A.K.; Walter, T.; Aronson, A.; Bashir, R. Microresonator mass sensors for detection of Bacillus anthracis Sterne spores in air and water. Biosens. Bioelectron. 2007, 22, 3028–3035. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Merzsch, S.; Waag, A.; Uhde, E.; Salthammer, T.; Peiner, E. Portable cantilever-based airborne nanoparticle detector. Sens. Actuators B Chem. 2013, 187, 118–127. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Merzsch, S.; Waag, A.; Uhde, E.; Salthammer, T.; Peiner, E. Airborne engineered nanoparticle mass sensor based on a silicon resonant cantilever. Sens. Actuators B Chem. 2013, 180, 77–89. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Merzsch, S.; Waag, A.; Uhde, E.; Salthammer, T.; Peiner, E. Evaluation of photoresist-based nanoparticle removal method for recycling silicon cantilever mass sensors. Sens. Actuators A Phys. 2013, 202, 90–99. [Google Scholar] [CrossRef]
- Wasisto, H.S.; Uhde, E.; Peiner, E. Enhanced performance of pocket-sized nanoparticle exposure monitor for healthy indoor environment. Build. Environ. 2016, 95, 13–20. [Google Scholar] [CrossRef]
- Dufour, I.; Josse, F.; Heinrich, S.M.; Lucat, C.; Ayela, C.; Ménil, F.; Brand, O. Unconventional uses of microcantilevers as chemical sensors in gas and liquid media. Sens. Actuators B Chem. 2012, 170, 115–121. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Yang, J.; Jun, S.; Mu, S.; Lan, Y. Simulation and Analysis of a Metamaterial Sensor Based on a Microring Resonator. Sensors 2011, 11, 5886–5899. [Google Scholar] [CrossRef] [Green Version]
- Shi, L.; Xu, Y.; Tan, W.; Chen, X. Simulation of optical microfiber loop resonators for ambient refractive index sensing. Sensors 2007, 7, 689–696. [Google Scholar] [CrossRef] [Green Version]
- Kwon, H.J.; Seok, S.; Lim, G. System Modeling of a MEMS Vibratory Gyroscope and Integration to Circuit Simulation. Sensors 2017, 17, 2633. [Google Scholar]
- Song, J.; He, C.; Wang, R.; Xue, C.; Zhang, W. A Mathematical Model of a Piezo-Resistive Eight-Beam Three-Axis Accelerometer with Simulation and Experimental Validation. Sensors 2018, 18, 3641. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Tian, Y.; Dan, J.; Bi, Z.; Zheng, J.; Li, B. Simulation-Based Design and Optimization of Accelerometers Subject to High-Temperature and High-Impact Loads. Sensors 2019, 19, 3759. [Google Scholar] [CrossRef] [Green Version]
- Feng, H.; Miao, X.; Yang, Z. Design, Simulation and Experimental Study of the Linear Magnetic Microactuator. Micromachines 2018, 9, 454. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64–76. [Google Scholar] [CrossRef] [Green Version]
- Van Eysden, C.A.; Sader, J.E. Resonant frequencies of a rectangular cantilever beam immersed in a fluid. J. Appl. Phys. 2006, 100, 114916. [Google Scholar] [CrossRef] [Green Version]
- Basak, S.; Raman, A.; Garimella, S.V. Hydrodynamic loading of microcantilevers vibrating in viscous fluids. J. Appl. Phys. 2006, 99, 114906. [Google Scholar] [CrossRef] [Green Version]
- Van Eysden, C.A.; Sader, J.E. Frequency response of cantilever beams immersed in compressible fluids with applications to the atomic force microscope. J. Appl. Phys. 2009, 106, 094904. [Google Scholar] [CrossRef]
- Van Eysden, C.A.; Sader, J.E. Compressible viscous flows generated by oscillating flexible cylinders. Phys. Fluids 2009, 21, 013104. [Google Scholar] [CrossRef] [Green Version]
- Xia, X.; Li, X. Resonance-mode effect on microcantilever mass-sensing performance in air. Rev. Sci. Instrum. 2008, 79, 074301. [Google Scholar] [CrossRef]
- Xie, H.; Vitard, J.; Haliyo, S.; Régnier, S. Enhanced sensitivity of mass detection using the first torsional mode of microcantilevers. Meas. Sci. Technol. 2008, 19, 055207. [Google Scholar] [CrossRef]
- Dohn, S.; Sandberg, R.; Svendsen, W.; Boisen, A. Enhanced functionality of cantilever-based mass sensors using higher modes. Appl. Phys. Lett. 2005, 86, 1–3. [Google Scholar] [CrossRef] [Green Version]
- Lochon, F.; Dufour, I.; Rebière, D. An alternative solution to improve sensitivity of resonant microcantilever chemical sensors: Comparison between using high-order modes and reducing dimensions. Sens. Actuators B Chem. 2004, 108, 979–985. [Google Scholar] [CrossRef]
- Qiu, H.; Xiao, D.; Feili, D.; Wu, X.; Seidel, H. Hydrodynamic analysis of piezoelectric microcantilevers vibrating in viscous compressible gases. Sens. Actuators A Phys. 2016, 238, 299–306. [Google Scholar] [CrossRef]
- Venstra, W.; Westra, H.; van der Zant, H. Stochastic switching of cantilever motion. Nat. Commun. 2013, 4, 2624. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ivaldi, P.; Abergel, J.; Matheny, M.; Villanueva, L.; Karabalin, R.; Roukes, M.; Andreucci, P.; Hentz, S.; Defay, E. 50 nm thick AlN film-based piezoelectric cantilevers for gravimetric detection. J. Micromech. Microeng. 2011, 21, 085023. [Google Scholar] [CrossRef] [Green Version]
- Ledermann, N.; Muralt, P.; Baborowski, J.; Forster, M.; Pellaux, J. Piezoelectric Pb(Zr-x,Ti1-x)O-3 thin film cantilever and bridge acoustic sensors for miniaturized photoacoustic gas detectors. J. Micromech. Microeng. 2004, 14, 1650–1658. [Google Scholar] [CrossRef]
- Keskar, G.; Elliott, B.; Gaillard, J.; Skove, M.; Rao, A. Using electric actuation and detection of oscillations in microcantilevers for pressure measurements. Sens. Actuators A Phys. 2008, 148, 472. [Google Scholar] [CrossRef]
- Chen, C.; Schwarz, A.; Wiesendanger, R.; Horn, O.; Muller, J. Three-electrode self-actuating self-sensing quartz cantilever: Design, analysis, and experimental verification. Rev. Sci. Instrum. 2010, 81, 053702. [Google Scholar] [CrossRef]
- Bhaskar, U.; Banerjee, N.B.; Abdollahi, A.; Wang, Z.; Schlom, D.; Rijnders, G.; Catalan, G. A flexoelectric microelectromechanical system on silicon. Nat. Nanotechnol. 2016, 11, 263. [Google Scholar] [CrossRef]
- Schwarz, K.; Rabe, U.; Hirsekorn, S.; Arnold, W. Excitation of atomic force microscope cantilever vibrations by a Schottky barrier. Appl. Phys. Lett. 2008, 92, 183105. [Google Scholar] [CrossRef]
- Penedo, M.; Raman, A.R.; Hormeno, S.H.; Fernandez-Martinez, I.; Luna, M.; Briones, F. Enhanced efficiency in the excitation of higher modes for atomic force microscopy and mechanical sensors operated in liquids. Appl. Phys. Lett. 2014, 105, 173102. [Google Scholar] [CrossRef]
- Huber, T.; Abell, B.; Mellema, D.; Spletzer, M.; Raman, A. Mode-selective noncontact excitation of microcantilevers and microcantilever arrays in air using the ultrasound radiation force. Appl. Phys. Lett. 2010, 97, 214101. [Google Scholar] [CrossRef] [Green Version]
- Marti, O.; Ruf, A.; Hipp, M.; Bielefeldt, H.; Colchero, J.; Mlynek, J. Mechanical and thermal effects of laser irradiation on force microscope cantilevers. Ultramicroscopy 1992, 42, 345–350. [Google Scholar] [CrossRef]
- Hoummady, M.; Farnault, E.; Yahiro, T.; Kawakatsu, H. Simultaneous optical detection techniques, interferometry, and optical beam deflection for dynamic mode control of scanning force microscopy. J. Vac. Sci. Technol. B 1997, 15, 1539–1542. [Google Scholar] [CrossRef]
- Rugar, D.; Mamin, H.J.; Guethner, P. Improved Fiber-Optic Interferometer for Atomic Force Microscopy. Appl. Phys. Lett. 1989, 55, 2588–2590. [Google Scholar] [CrossRef]
- Thaysen, J.; Boisen, A.; Hansen, O.; Bouwstra, S. Atomic force microscopy probe with piezoresistive read-out and a highly symmetrical Wheatstone bridge arrangement. Sens. Actuators A Phys. 2000, 83, 47–53. [Google Scholar] [CrossRef]
- Linnemann, R.; Gotszalk, T.; Hadjiiski, L.; Rangleow, I. Characterization of a Cantilever with an Integrated Deflection Sensor. Thin Solid Films 1995, 264, 159–164. [Google Scholar] [CrossRef]
- Shin, S.; Kim, J.; Sim, S.; Lee, J. A multisized piezoelectric microcantilever biosensor array for the quantitative analysis of mass and surface stress. Appl. Phys. Let. 2008, 93, 102902. [Google Scholar] [CrossRef]
- Verd, J.; Abadal, G.; Teva, J.; Gaudo, M.; Uranga, A.; Borrise, X.; Campabadal, F.; Esteve, J.; Costa, E.; Perez-Murano, F.; et al. Design, fabrication, and characterization of a submicroelectromechanical resonator with monolithically integrated CMOS readout circuit. J. Microelectromech. Syst. 2005, 14, 508–519. [Google Scholar] [CrossRef]
- Kenny, T.; Kaiser, W.; Podosek, J.; Rockstad, H.; Reynolds, J.; Vote, E. Micromachined Tunneling Displacement Transducers for Physical Sensors. J. Vac. Sci. Technol. A Vac. Surfaces Films 1993, 11, 797–802. [Google Scholar] [CrossRef]
- Rabe, U.; Janser, K.; Arnold, W. Vibrations of free and surface-coupled atomic force microscope cantilevers: Theory and experiment. Rev. Sci. Instrum. 1996, 67, 3281–3293. [Google Scholar] [CrossRef]
- Van Eysden, C.; Sader, J. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope: Arbitrary mode order. J. Appl. Phys. 2008, 104, 109901. [Google Scholar] [CrossRef]
- Coppola, G.; Capuano, F.; de Luca, L. Discrete Energy-Conservation Properties in the Numerical Simulation of the Navier-Stokes Equations. Appl. Mech. Rev. 2019, 71, 010803. [Google Scholar] [CrossRef]
- Ikeda, T.; Ueda, T.; Nakata, T.; Noda, R.; Tanaka, H.; Fujii, T.; Liu, H. Morphology Effects of Leading-edge Serrations on Aerodynamic Force Production: An Integrated Study Using PIV and Force Measurements. J. Bionic Eng. 2018, 15, 661–672. [Google Scholar] [CrossRef]
- Rao, C.; Ikeda, T.; Nakata, T.; Liu, H. Owl-inspired leading-edge serrations play a crucial role in aerodynamic force production and sound suppression. Bioinspir. Biomim. 2017, 12, 046008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bednorz, A. Sutherland formula for a square-well fluid. Phys. Rev. E 2006, 73, 011203. [Google Scholar] [CrossRef] [PubMed]
- Akaogi, M. Clapeyron’s Equation. In Encyclopedia of Geochemistry; William, M.W., Ed.; Department of Earth, Cornell University Department of Earth; Springer: Ithaca, NY, USA, 2017. [Google Scholar]
- Blackstock, D.T. Fundamentals of Physical Acoustics. J. Acoust. Soc. Am. 2001, 4, 1274–1276. [Google Scholar] [CrossRef]




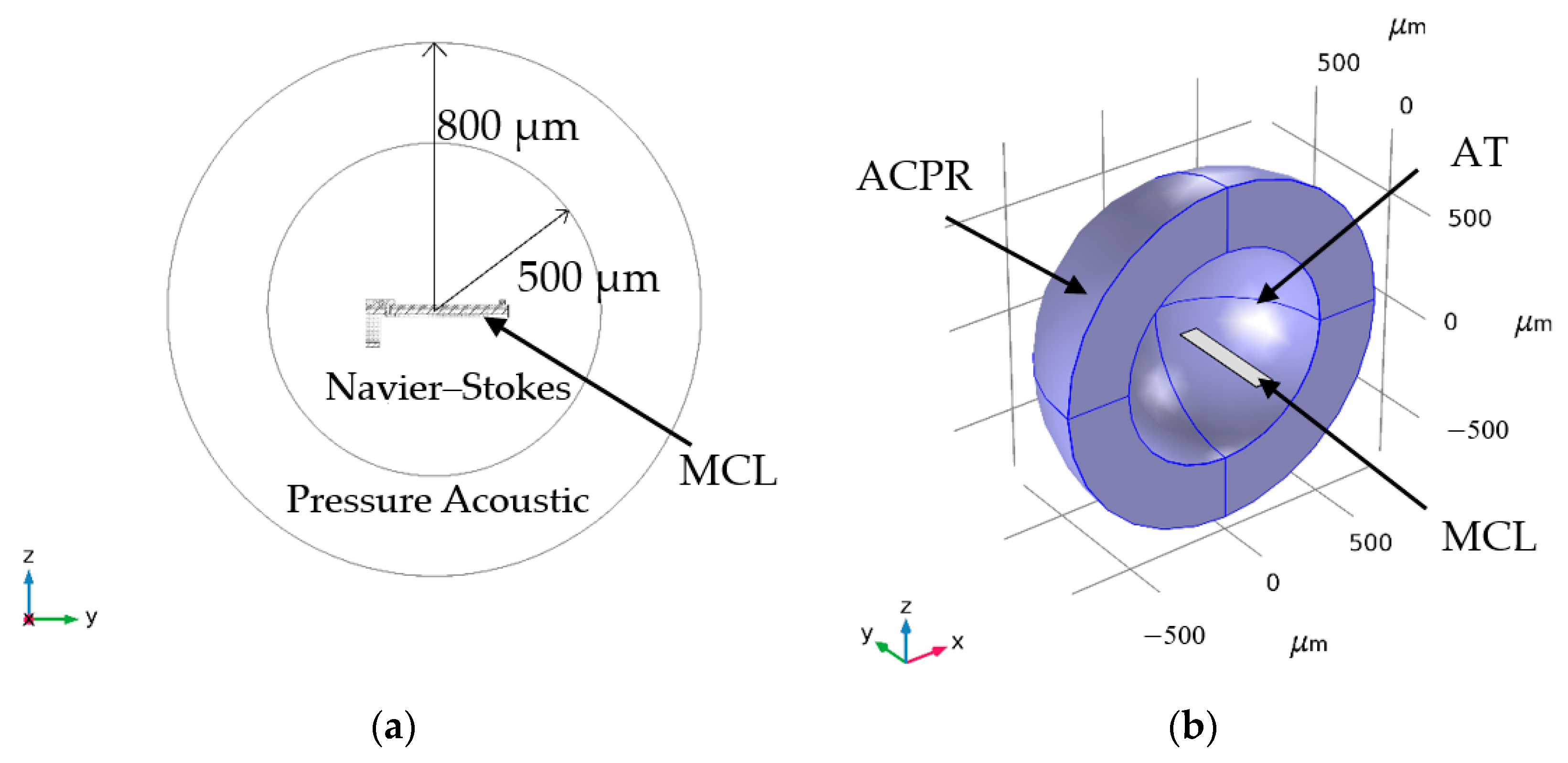


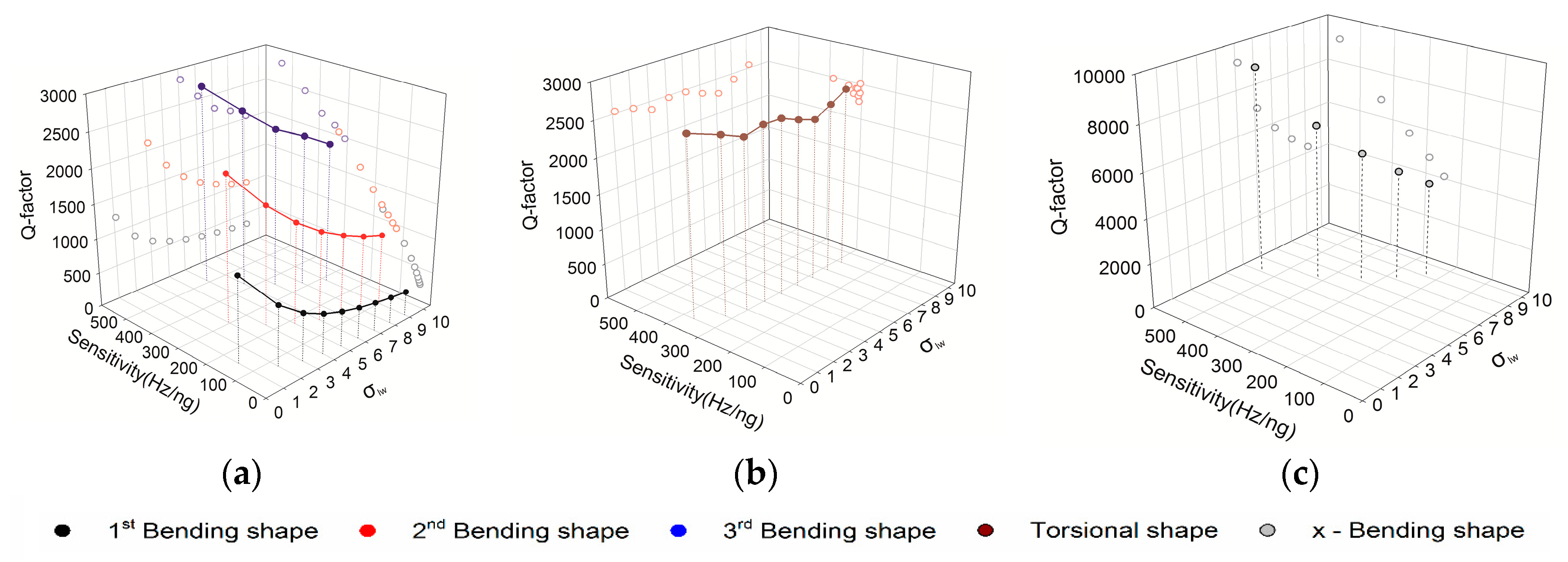

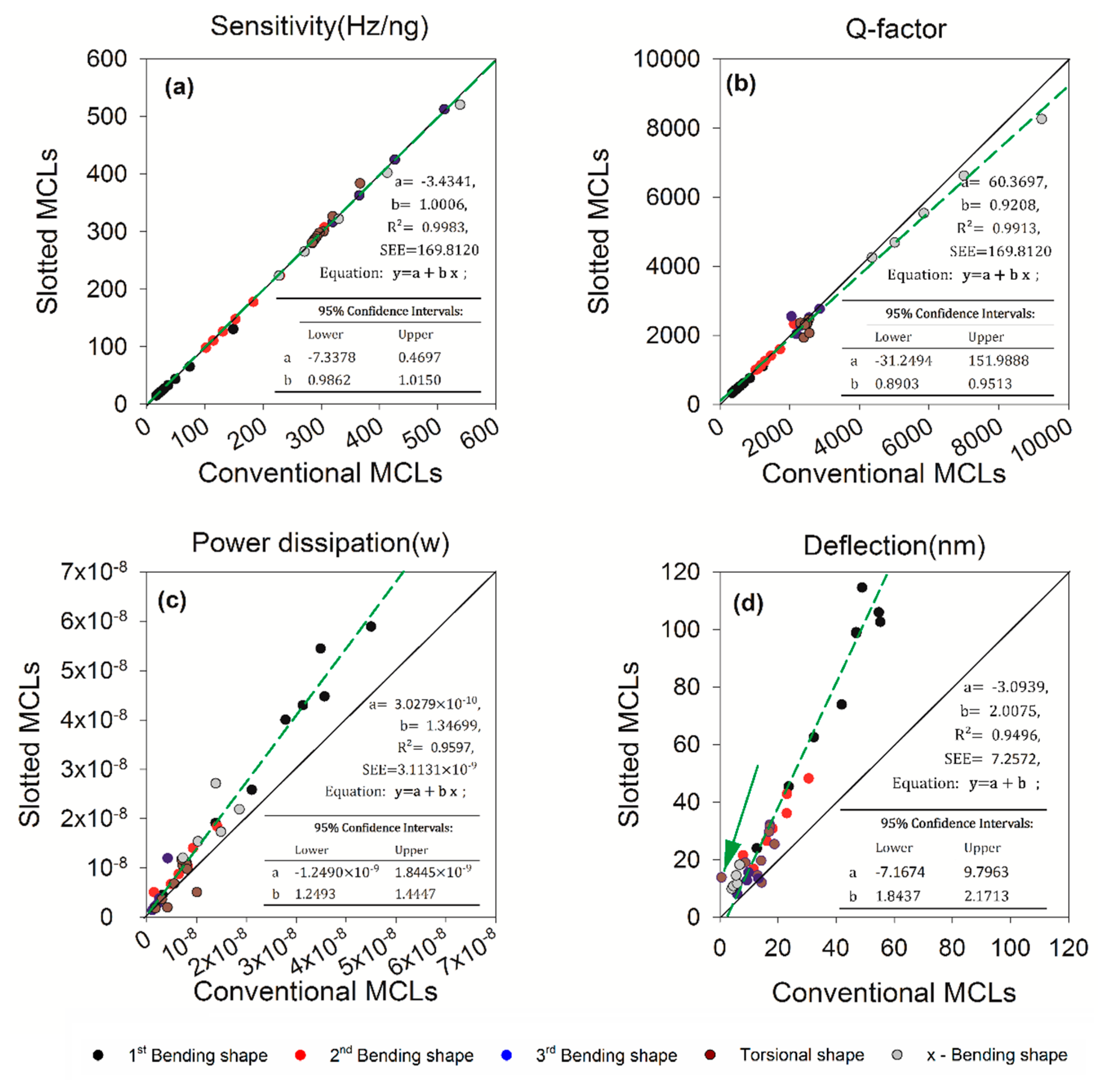
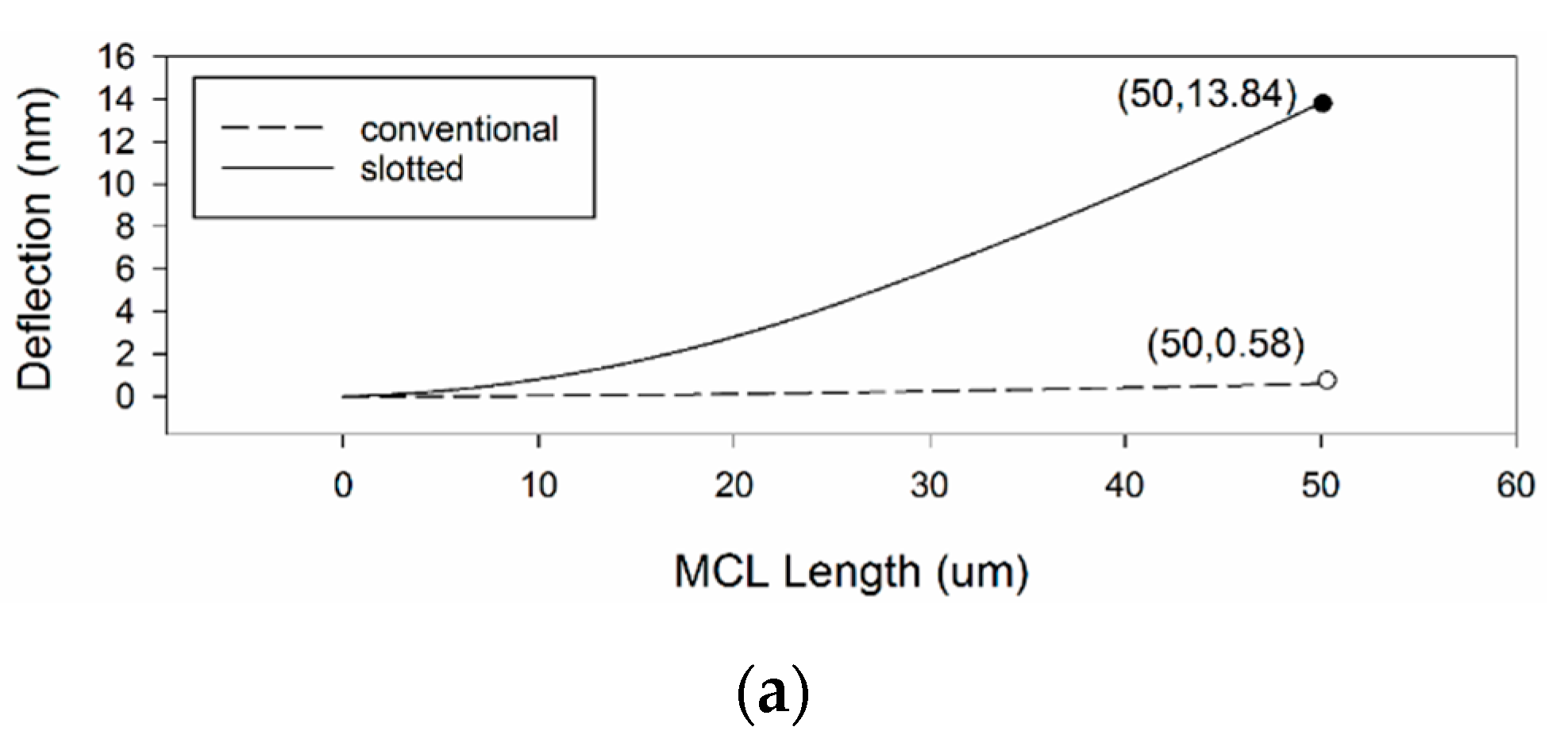
| Property | Value | Unit |
|---|---|---|
| Density | 2329 | kg/m3 |
| Young’s modulus | 170 | G Pa |
| Poisson’s ratio | 0.28 | 1 |
| Thermal expansion coefficient | 2.6 × 106 | 1/K |
| Thermal conductivity | 130 | W/(m·K) |
| Heat capacity at constant pressure | 700 | J/(kg·K) |
| Experimental | Simulation | |||||
|---|---|---|---|---|---|---|
| Frequency (Hz) | Sensitivity (Hz/ng) | Q | Frequency (Hz) | Sensitivity (Hz/ng) | Q | |
| 1250 × 26.5 × 39.3 [13] | ~221,502.36 | 36.5 | ~1950 | 216,460.77 | 35.58 | 1901.17 |
| 1250 × 30 × 25 [14] | ~43,900 | ~10 | ~1206 | 46,703.92 | 10.46 | 1147.52 |
| 1000 × 170 × 19 [16] | ~201,950 | No report | ~4702 | 229,915.23 | 15.29 | 4789.90 |
| 2750 × 100 × 50 [15,16] | ~9365.35 | No report | ~1665 | 9126.54 | 0.14 | 1250.21 |
| ~56,998.64 | 0.91 | ~1814 | 57,116.37 | 0.89 | 1643.16 | |
| ~159,597.82 | No report | ~1383 | 159,532.14 | 2.48 | 1437.53 | |
| 5000 × 200 × 40 [15] | ~2201.04 | No report | ~502 | 2207.74 | 0.02 | 490.60 |
| ~13,793.67 | 0.07 | ~1335 | 13,840.52 | 0.07 | 1274.45 | |
| ~38,622.67 | No report | ~1955 | 38,744.43 | 0.20 | 2094.29 | |
| Resonant Mode | Actuating Method | Signal Read-Out Method |
|---|---|---|
| Bending | piezoelectric, electric, flexoelectric, atomic force, magnetic, ultrasound radiation force and laser irradiation | optics, piezoresistance, piezoelectricity, capacitive, tunneling |
| Torsional | magnetic | optics, piezoresistance, piezoelectricity |
| Resonant Mode | Types of Micro Cantilever | Max Temperature Variation (K) |
|---|---|---|
| 1st Bending mode | No serrations | 1.796 × 10−3 |
| With serrations | 0.481 × 10−3 | |
| Torsional mode | No serrations | 2.928 × 10−3 |
| With serrations | 0.263 × 10−3 |
| Resonant Mode | Types of Micro Cantilever | Total Dissipation (W) | Thermal Dissipation (W) | Viscous Dissipation (W) |
|---|---|---|---|---|
| 1st Bending mode | No serrations | 1.575 × 10−8 | 8.254 × 10−13 | 1.575 × 10−8 |
| With serrations | 0.116 × 10−8 | 0.578 × 10−13 | 0.116 × 10−8 | |
| Torsional mode | No serrations | 4.174 × 10−9 | 4.564 × 10−12 | 4.170 × 10−9 |
| With serrations | 0.338 × 10−8 | 0.219 × 10−12 | 0.339 × 10−9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, F.; Wei, Y.; Bian, S.; Wang, H.; Chen, D.-R.; Kong, D. Simulation-Based Design and Optimization of Rectangular Micro-Cantilever-Based Aerosols Mass Sensor. Sensors 2020, 20, 626. https://doi.org/10.3390/s20030626
Xu F, Wei Y, Bian S, Wang H, Chen D-R, Kong D. Simulation-Based Design and Optimization of Rectangular Micro-Cantilever-Based Aerosols Mass Sensor. Sensors. 2020; 20(3):626. https://doi.org/10.3390/s20030626
Chicago/Turabian StyleXu, Feng, Yuliang Wei, Shiyuan Bian, Huanqin Wang, Da-Ren Chen, and Deyi Kong. 2020. "Simulation-Based Design and Optimization of Rectangular Micro-Cantilever-Based Aerosols Mass Sensor" Sensors 20, no. 3: 626. https://doi.org/10.3390/s20030626
APA StyleXu, F., Wei, Y., Bian, S., Wang, H., Chen, D.-R., & Kong, D. (2020). Simulation-Based Design and Optimization of Rectangular Micro-Cantilever-Based Aerosols Mass Sensor. Sensors, 20(3), 626. https://doi.org/10.3390/s20030626





