Generating and Detecting Solvable Chaos at Radio Frequencies with Consideration to Multi-User Ranging
Abstract
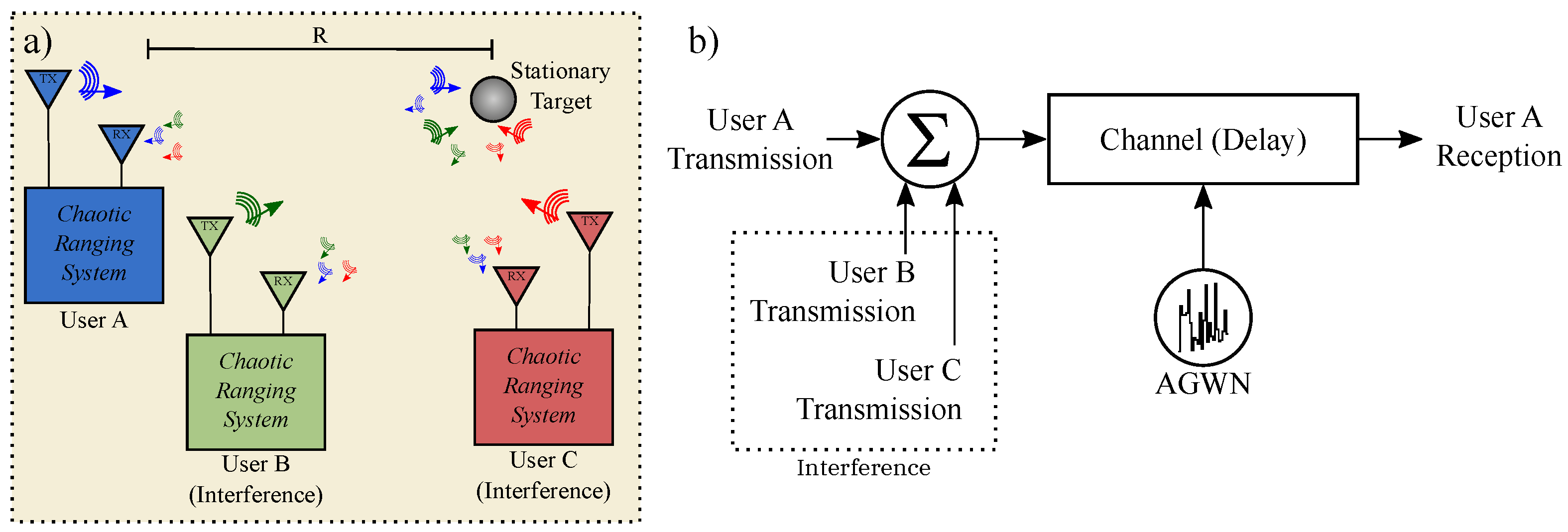
1. Introduction
2. Background
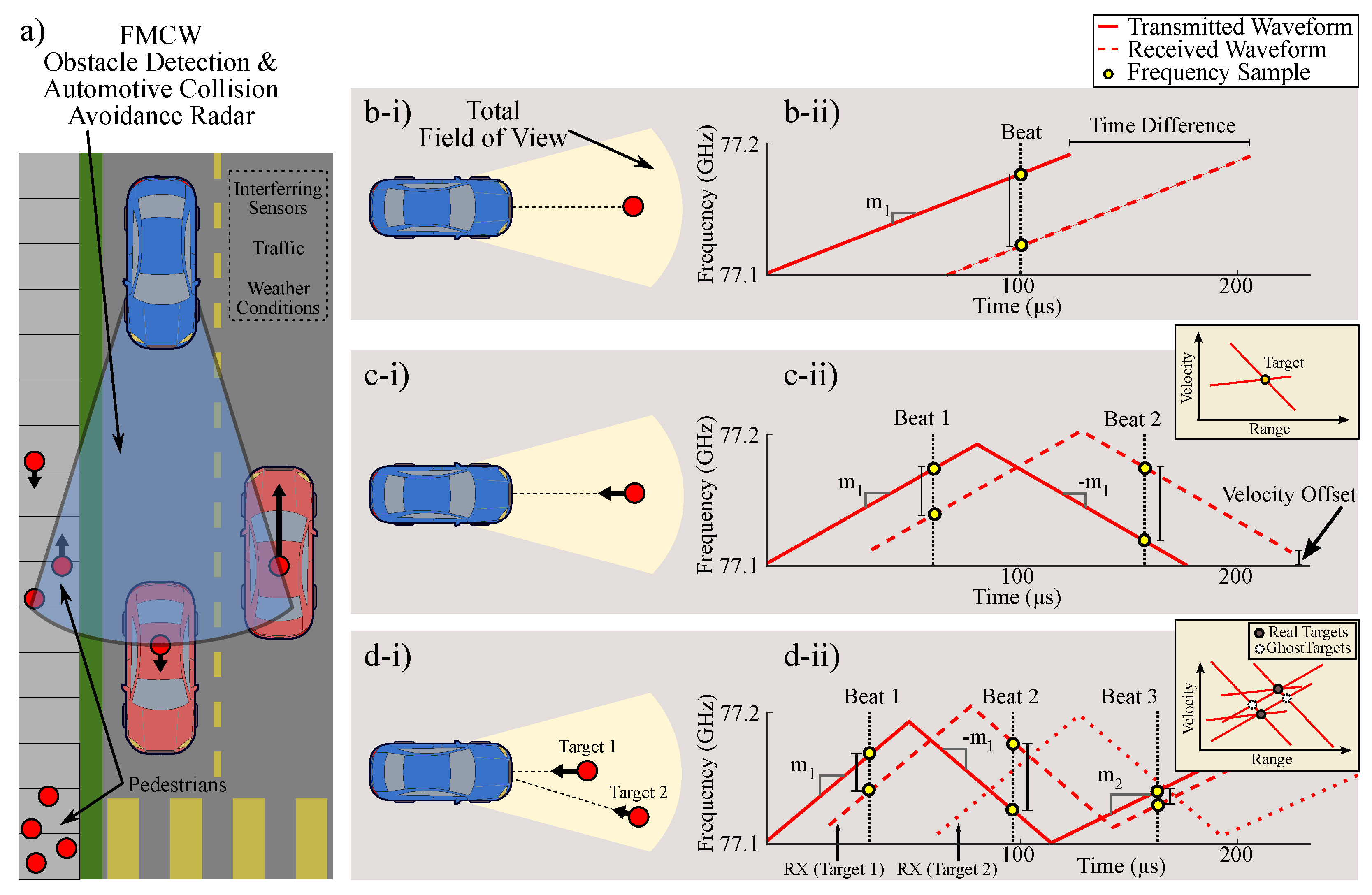
2.1. FMCW Limitations
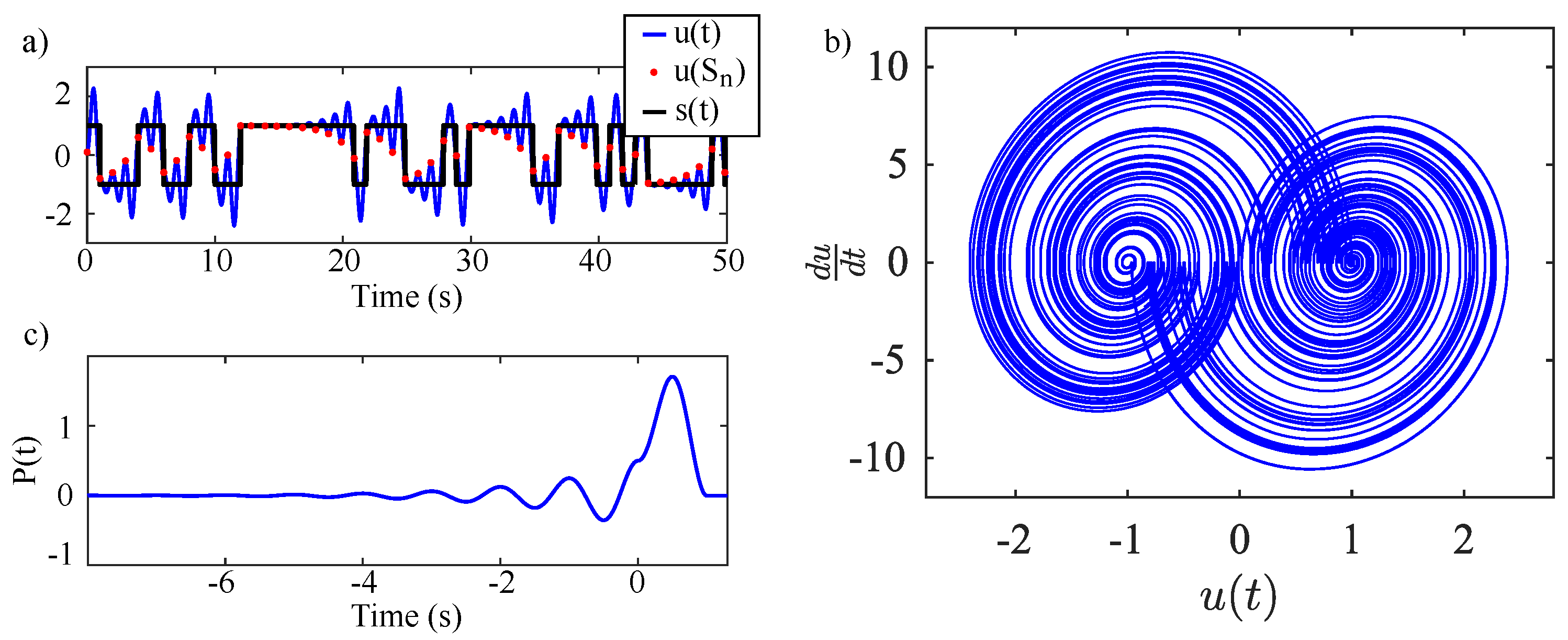
2.2. Solvable Chaos
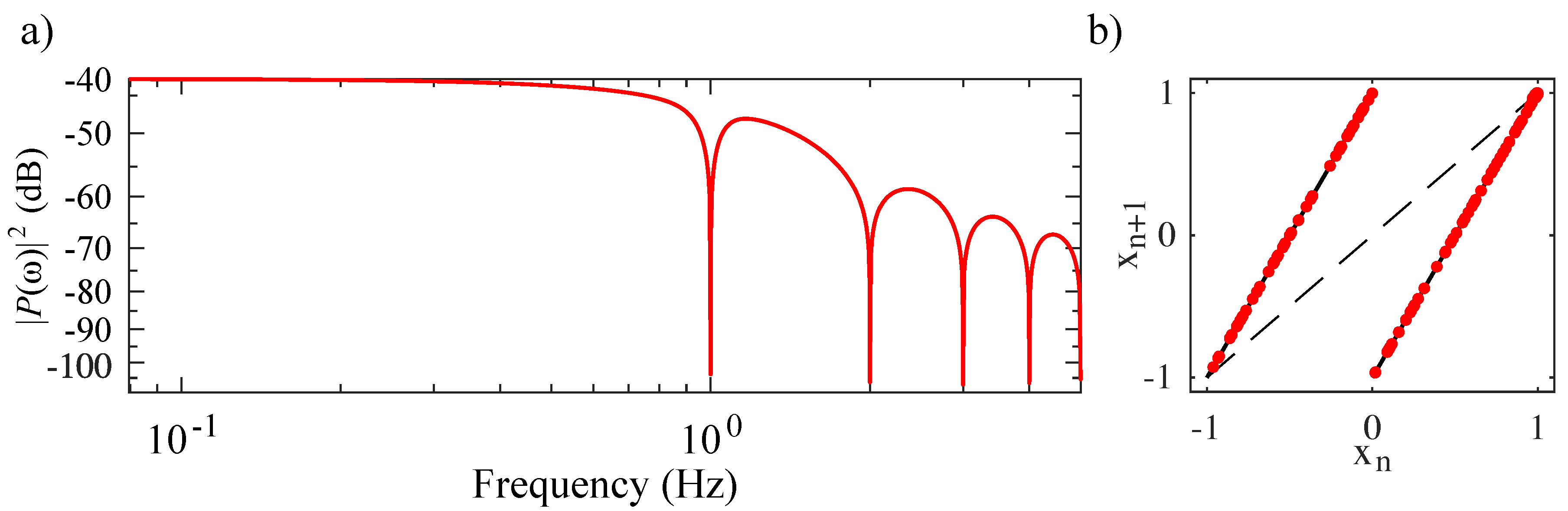
2.2.1. Solvable Chaos Theory
2.2.2. Simple, Optimal Detection
3. Hardware Design
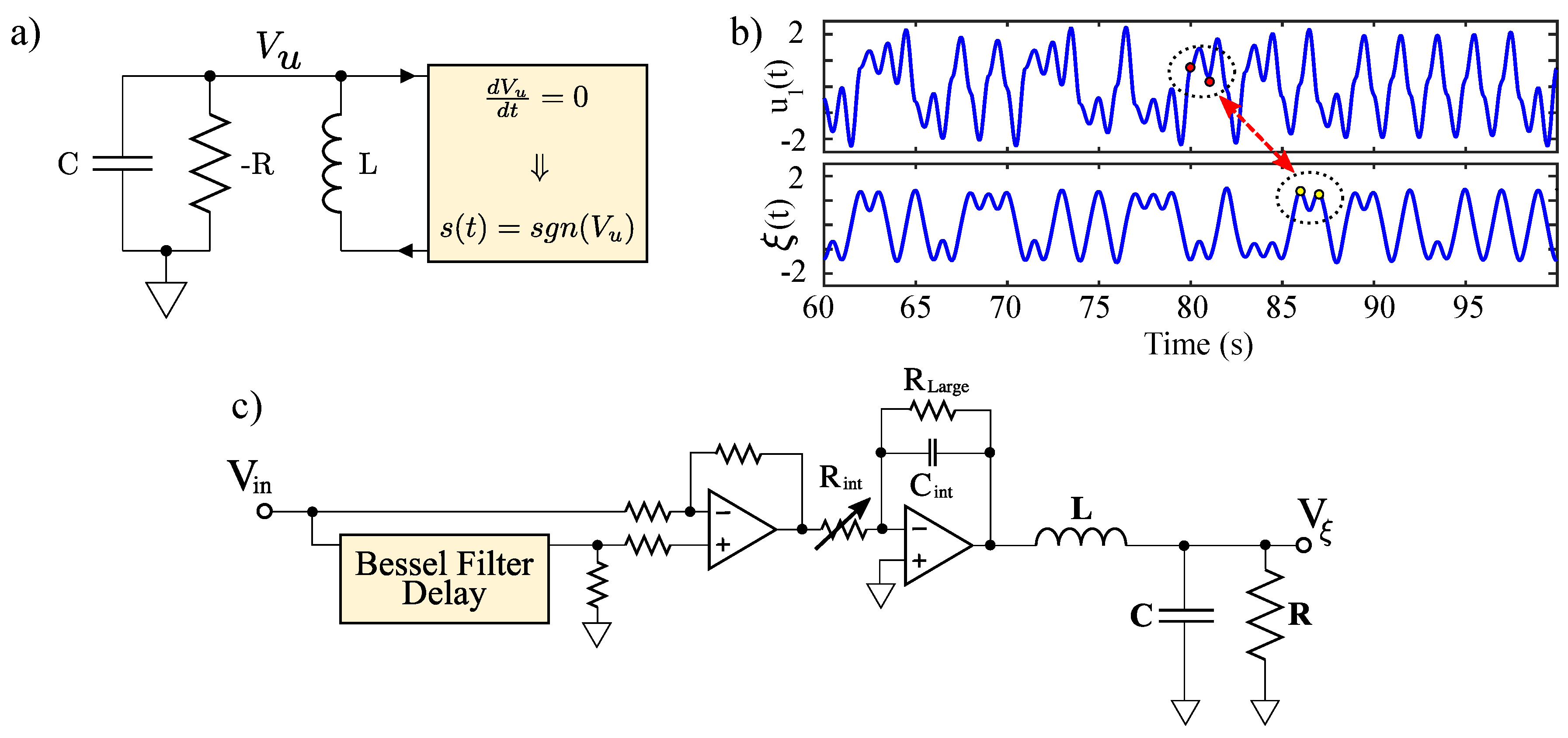
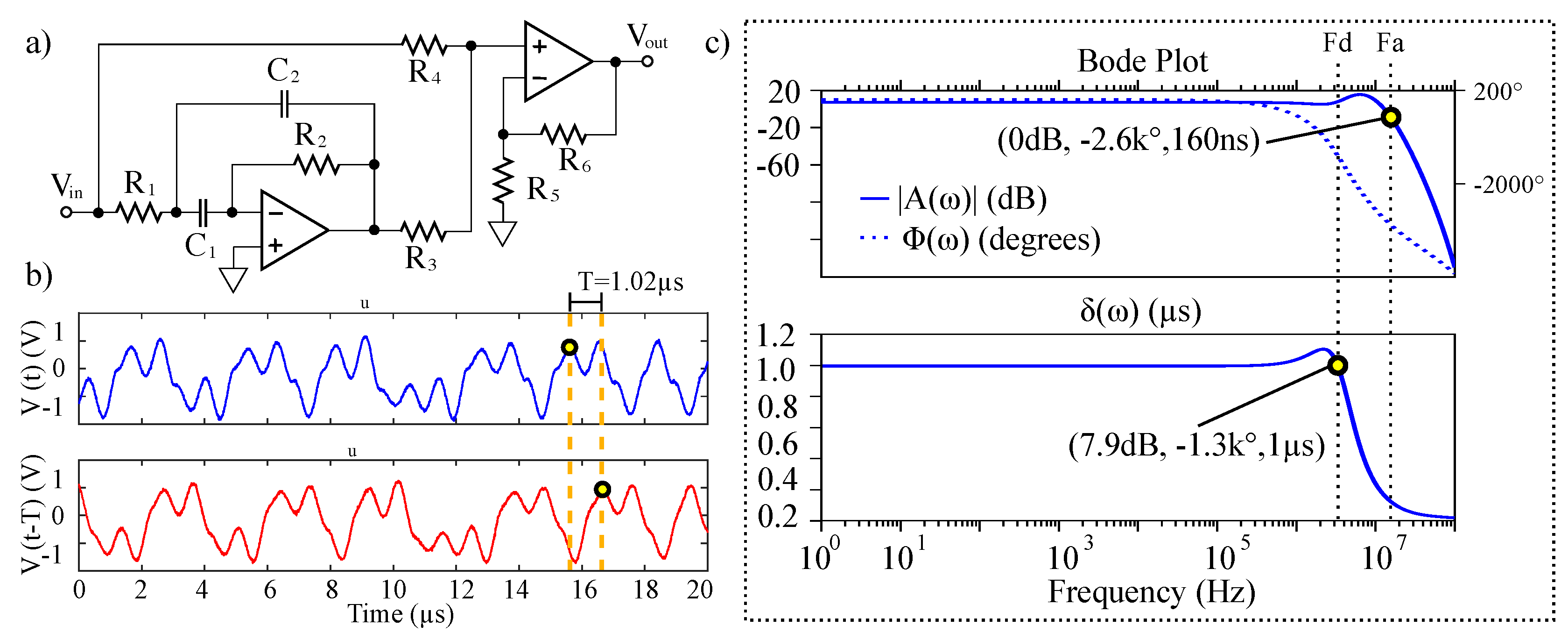
3.1. Generating Solvable Chaos at Radio Frequencies
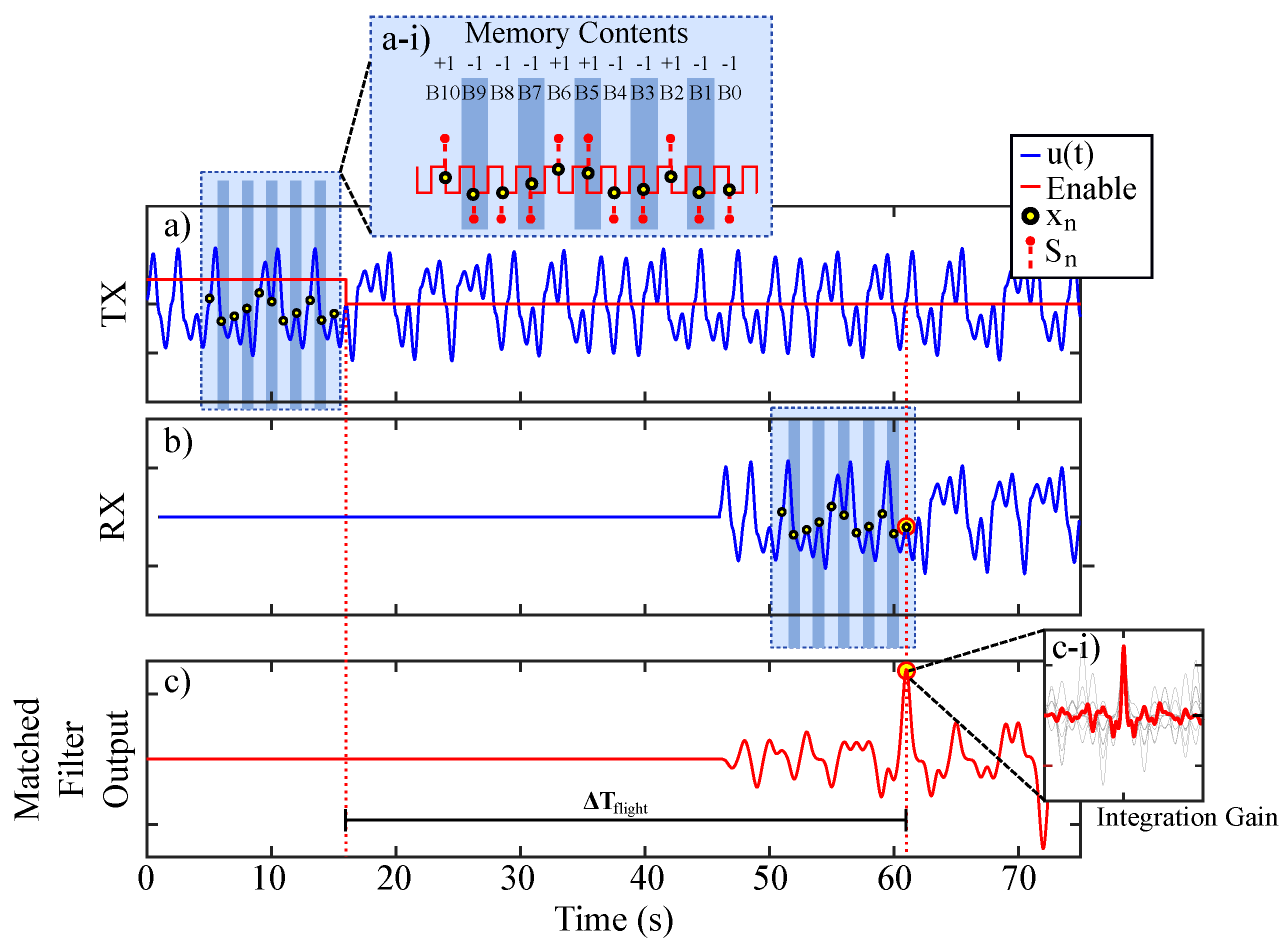
3.2. Matched Filter Detection
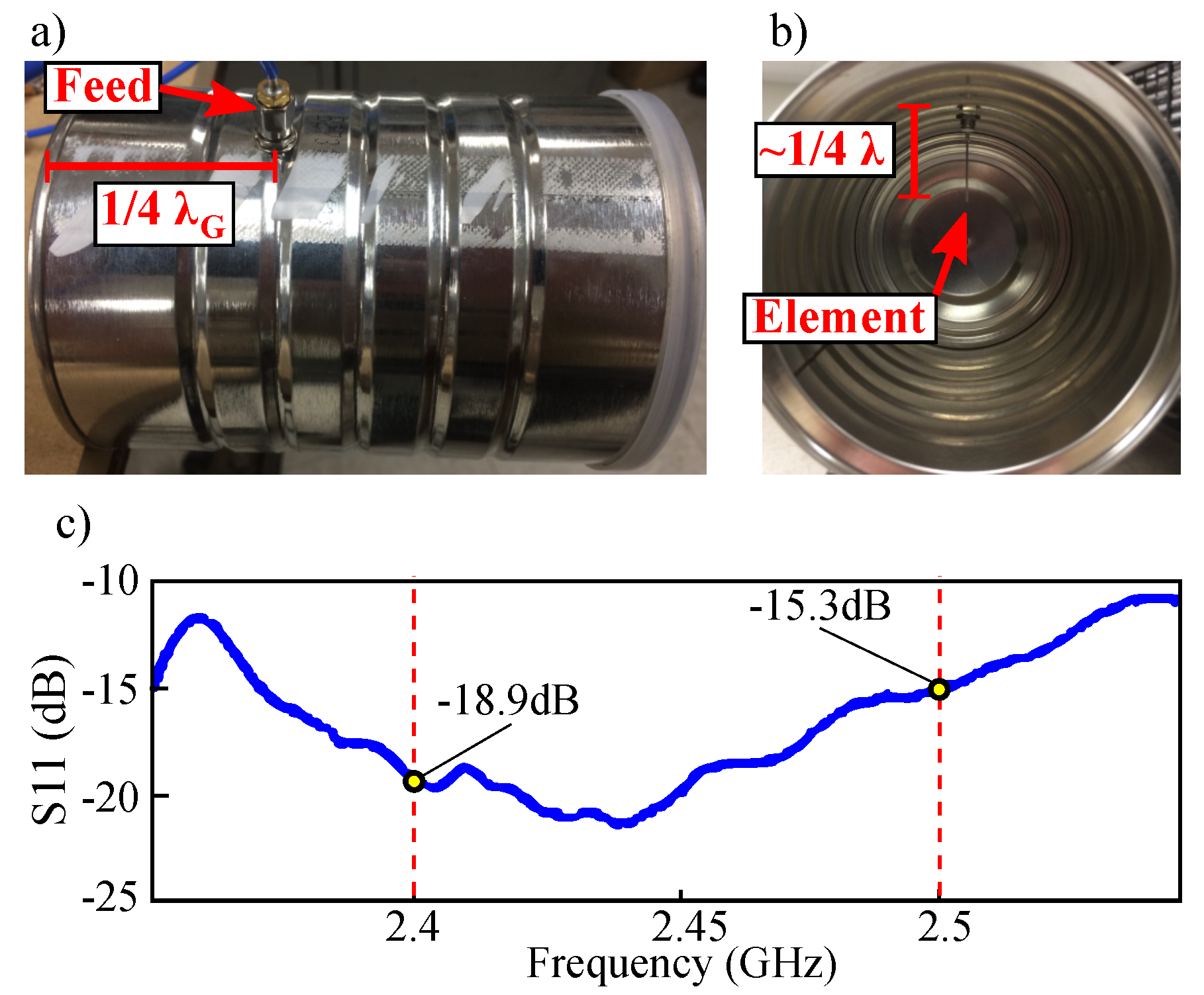
3.3. Wireless Transmission
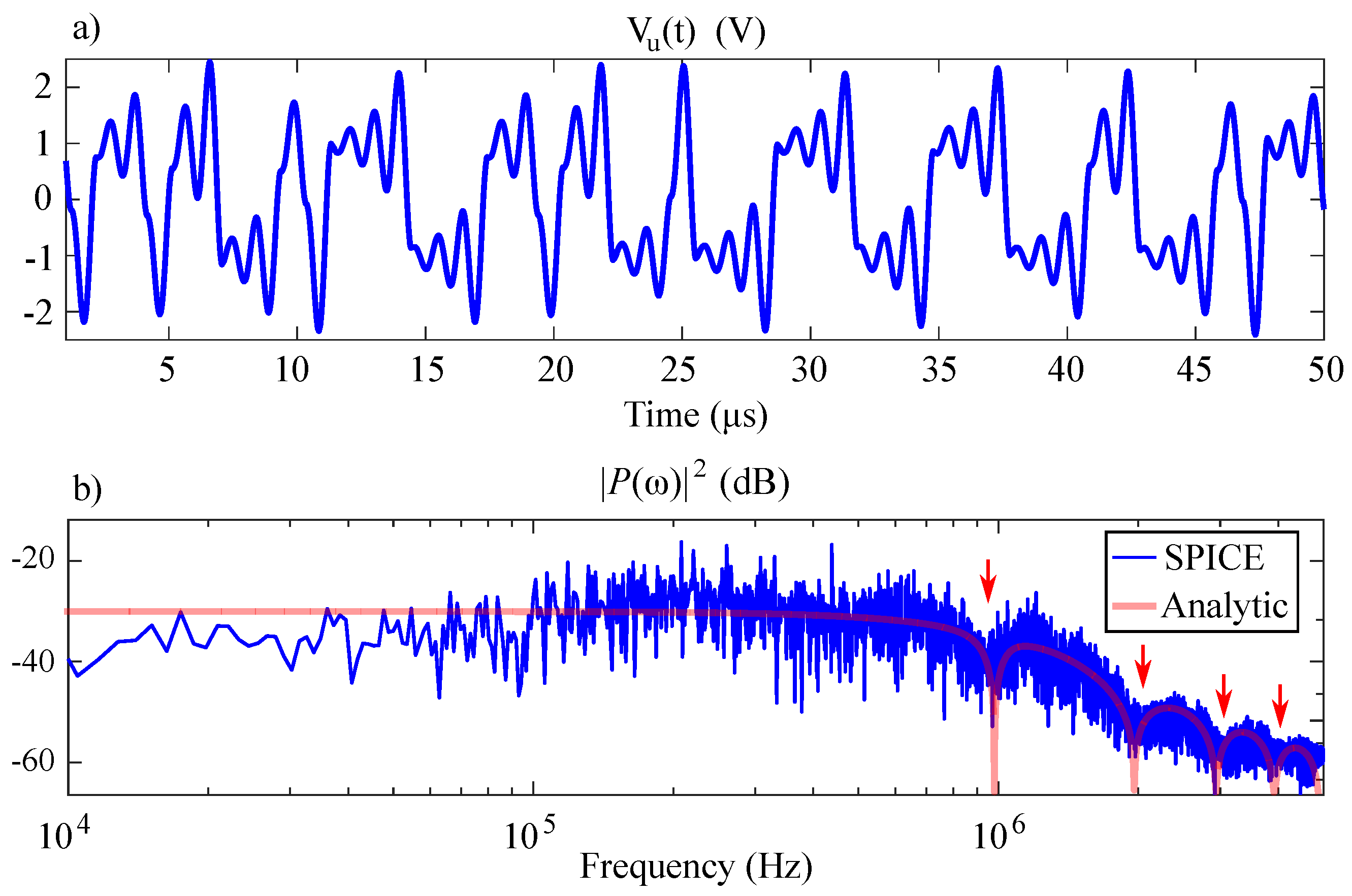
4. Results
5. Discussion
5.1. Environmental Sensing Scheme
5.2. Multi-User Concept
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AGWN | Additive Gaussian white noise |
| AM | Amplitude modulation |
| BER | Bit error rate |
| BPSK | Binary phase-shift keying |
| CDMA | Code division multiple access |
| COTS | Consumer off-the-shelf |
| CW | Continuous wave |
| DSP | Digital signal processor |
| DOAJ | Directory of open access journals |
| FFT | Fast Fourier Transform |
| FM | Frequency modulation |
| FMCW | Frequency modulated continuous wave |
| FPGA | Field programmable gate array |
| IoT | Internet of Things |
| MDPI | Multidisciplinary Digital Publishing Institute |
| NIC | Negative impedance converter |
| op-amp | Operational Amplifier |
| RF | Radio frequency |
| RLC | Resistor, inductor, capacitor |
| -RLC | Negative resistor, inductor, capacitor |
| SNR | Signal-to-noise Ratio |
| UWB | Ultra-wideband |
References
- Gubbi, J.; Buyya, R.; Marusic, S.; Palaniswami, M. Internet of Things (IoT): A vision, architectural elements, and future directions. Future Gener. Comput. Syst. 2013, 29, 1645–1660. [Google Scholar] [CrossRef]
- Da Xu, L.; He, W.; Li, S. Internet of things in industries: A survey. IEEE Trans. Ind. Inf. 2014, 10, 2233–2243. [Google Scholar] [CrossRef]
- Liu, L.; Popescu, M.; Skubic, M.; Rantz, M.; Yardibi, T.; Cuddihy, P. Automatic fall detection based on Doppler radar motion signature. In Proceedings of the 5th International Conference on Pervasive Computing Technologies for Healthcare (PervasiveHealth) and Workshops, Dublin, Ireland, 23–26 May 2011. [Google Scholar] [CrossRef]
- Jin, F.; Cao, S. Automotive radar interference mitigation using adaptive noise canceller. IEEE Trans. Veh. Technol. 2019, 68, 3747–3754. [Google Scholar] [CrossRef]
- Besada, J.A.; Bernardos, A.M.; Bergesio, L.; Vaquero, D.; Campaña, I.; Casar, J.R. Drones-as-a-service: A management architecture to provide mission planning, resource brokerage and operation support for fleets of drones. In Proceedings of the 2019 IEEE International Conference on Pervasive Computing and Communications Workshops (PerCom Workshops), Kyoto, Japan, 11–15 March 2019. [Google Scholar] [CrossRef]
- Tanis, S. Automotive radar and congested spectrum: Potential urban electronic battlefield. Microwave J. 2019, 62, 48–56. [Google Scholar]
- Buller, W.; Wilson, B.; Garbarino, J.; Kelly, J.; Thelen, B.; Belzowski, B.M. Radar Congestion Study. No. DOT HS 812 632. USA. Department of Transportation. National Highway Traffic Safety Administration, 2018. Available online: https://rosap.ntl.bts.gov/view/dot/38820 (accessed on 15 January 2020).
- Goppelt, M.; Blöcher, H.L.; Menzel, W. Analytical investigation of mutual interference between automotive FMCW radar sensors. In Proceedings of the 2011 German Microwave Conference, Darmstadt, Germany, 14–16 March 2011. [Google Scholar]
- Van Brummelen, J.; O’Brien, M.; Gruyer, D.; Najjaran, H. Autonomous vehicle perception: The technology of today and tomorrow. Transp. Res. Part C Emerg. Technol. 2018, 89, 384–406. [Google Scholar] [CrossRef]
- Jörg, K.W.; Berg, M. Sophisticated mobile robot sonar sensing with pseudorandom codes. Rob. Autom. Syst. 1998, 25, 241–251. [Google Scholar] [CrossRef]
- Meng, Q.H.; Lan, S.Y.; Yao, Z.J.; Li, G.W. Real-time noncross-talk sonar system by short optimized pulse-position modulation sequences. IEEE Trans. Instrum. Meas. 2009, 58, 3442–3449. [Google Scholar] [CrossRef]
- Theron, I.P.; Walton, E.K.; Gunawan, S.; Cai, L. Ultrawide-band noise radar in the VHF/UHF band. IEEE Trans. Antennas Propag. 1999, 47, 1080–1084. [Google Scholar] [CrossRef]
- Dawood, M.; Narayanan, R.M. Receiver operating characteristics for the coherent UWB random noise radar. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 586–594. [Google Scholar] [CrossRef]
- Liu, T.H.; Hsu, M.L.; Tsai, Z.M. Mutual interference of pseudorandom noise radar in automotive collision avoidance application at 24 GHz. In Proceedings of the 2016 IEEE 5th Global Conference on Consumer Electronics, Kyoto, Japan, 11–14 October 2016. [Google Scholar] [CrossRef]
- Son, Y.S.; Sung, H.K.; Heo, S.W. Automotive frequency modulated continuous wave radar interference reduction using per-vehicle chirp sequences. Sensors 2018, 18, 2831. [Google Scholar] [CrossRef] [PubMed]
- Corron, N.J.; Blakely, J.N.; Stahl, M.T. A matched filter for chaos. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 023123. [Google Scholar] [CrossRef] [PubMed]
- Corron, N.J. Compensation for imperfect switching in a chaotic hybrid oscillator circuit. In Proceedings of the 2015 IEEE 58th International Midwest Symposium on Circuits and Systems (MWSCAS), Fort Collins, CO, USA, 2–5 August 2015. [Google Scholar] [CrossRef]
- Beal, A.N.; Bailey, J.P.; Hale, S.A.; Dean, R.N.; Hamilton, M.; Tugnait, J.K.; Hahs, D.W.; Corron, N.J. Design and simulation of a high frequency exact solvable chaotic oscillator. In Proceedings of the 2012 IEEE Military Communications MILCOM Conference, Orlando, FL, USA, 28–31 October 2012. [Google Scholar] [CrossRef]
- Corron, N.J.; Stahl, M.T.; Harrison, R.C.; Blakely, J.N. Acoustic detection and ranging using solvable chaos. Chaos Interdiscip. J. Nonlinear Sci. 2013, 23, 023119. [Google Scholar] [CrossRef] [PubMed]
- Lai, C.P.; Narayanan, R.M. Ultrawideband random noise radar design for through-wall surveillance. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1716–1730. [Google Scholar] [CrossRef]
- Wang, Z.; Wu, Y.; Niu, Q. Multi-Sensor Fusion in Automated Driving: A Survey. IEEE Access 2020, 8, 2847–2868. [Google Scholar] [CrossRef]
- Rasshofer, R.H.; Gresser, K. Automotive radar and lidar systems for next generation driver assistance functions. Adv. Radio Sci. 2005, 3, 205–209. [Google Scholar] [CrossRef]
- Meng, Q.; Yao, F.; Wu, Y. Review of cross-talk elimination methods for ultrasonic range systems in mobile robots. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9 October 2006. [Google Scholar] [CrossRef]
- Abreu, P.; Antonelli, G.; Arrichiello, F.; Caffaz, A.; Caiti, A.; Casalino, G.; Volpi, N.C.; De Jong, I.B.; De Palma, D.; Duarte, H.; et al. Widely scalable mobile underwater sonar technology: An overview of the H2020 WiMUST project. Mar. Technol. Soc. J. 2016, 50, 42–53. [Google Scholar] [CrossRef]
- Bor-Yaliniz, I.; Yanikomeroglu, H. The new frontier in RAN heterogeneity: Multi-tier drone-cells. IEEE Commun. Mag. 2016, 54, 48–55. [Google Scholar] [CrossRef]
- Mozaffari, M.; Saad, W.; Bennis, M.; Debbah, M. Drone small cells in the clouds: Design, deployment and performance analysis. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6 December 2015. [Google Scholar]
- Yoshikawa, K.; Yamashita, S.; Yamamoto, K.; Nishio, T.; Morikura, M. Resource allocation for 3d drone networks sharing spectrum bands. In Proceedings of the IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 12 February 2018. [Google Scholar]
- Ng, H.J.; Feger, R.; Stelzer, A. A fully-integrated 77-GHz UWB pseudorandom noise radar transceiver with a programmable sequence generator in SiGe technology. IEEE Trans. Circuits Syst. Regul. Pap. 2014, 61, 2444–2455. [Google Scholar] [CrossRef]
- Skolnik, M.I. Introduction to Radar Systems; McGraw Hill Book Co.: New York, NY, USA, 1980; p. 590. [Google Scholar]
- Scheer, J.; William, A.H. Principles of Modern Radar; Richards, M.A., Melvin, W.L., Eds.; SciTech Pub.: Edison, NJ, USA, 2010. [Google Scholar]
- Heuel, S.; Schmitt, H. Rohde & Schwarz (Producer) Rohde & Schwarz Webinar: Analysis of FMCW Radar Signals in Automotive Applications. 2014. Available online: https://youtu.be/8qaCSQ83ZyU (accessed on 5 December 2019).
- Heuel, S.; Rohling, H. Pedestrian recognition in automotive radar sensors. In Proceedings of the IEEE 14th International Radar Symposium (IRS), Dresden, Germany, 19 June 2013. [Google Scholar]
- Jansson, J. Collision Avoidance Theory: With Application to aUtomotive Collision Mitigation. Ph.D. Thesis, Linköping University Electronic, Linköping, Sweden, 3 June 2005. [Google Scholar]
- Heuel, S. Automotive radar interference test. In Proceedings of the 18th International Radar Symposium (IRS), Prague, Czech Republic, 28–30 June 2017. [Google Scholar] [CrossRef]
- Rohling, H.; Heuel, S.; Ritter, H. Pedestrian detection procedure integrated into an 24 GHz automotive radar. In Proceedings of the IEEE Radar Conference, Washington, DC, USA, 10 May 2010. [Google Scholar] [CrossRef]
- Komissarov, R.; Kozlov, V.; Filonov, D.; Ginzburg, P. Partially coherent radar unties range resolution from bandwidth limitations. Nat. Commun. 2019, 10, 1423. [Google Scholar] [CrossRef]
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; Westview Press: Boulder, CO, USA, 2018. [Google Scholar]
- Shinbrot, T.; Grebogi, C.; Yorke, J.A.; Ott, E. Using small perturbations to control chaos. Nature 1993, 363, 411–417. [Google Scholar] [CrossRef]
- Hayes, S.; Grebogi, C.; Ott, E. Communicating with chaos. Phys. Rev. Lett. 1993, 70, 3031. [Google Scholar] [CrossRef] [PubMed]
- Hayes, S. Chaos from linear systems: Implications for communicating with chaos, and the nature of determinism and randomness. J. Phys. Conf. Ser. 2005, 23, 215. [Google Scholar] [CrossRef]
- Corron, N.J.; Blakely, J.N. Chaos in optimal communication waveforms. Proc. R. Soc. A 2015, 471, 20150222. [Google Scholar] [CrossRef]
- Middleton, D. An Introduction to Statistical Communication Theory; McGraw-Hill: New York, NY, USA, 1960. [Google Scholar]
- McGillem, C.D.; Cooper, G.R. Probabilistic Methods of Signal and System Analysis; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Beal, A.N. Analog Computation of a High Frequency Exactly Solvable Chaotic Communications System Using State Variable Networks. Ph.D. Thesis, Auburn University, Auburn, AL, USA, 2015. [Google Scholar]
- Blakely, J.N.; Corron, N.J. Ambiguity in range: Doppler determination using waveforms of a solvable chaotic oscillator. Signal Process. 2014, 104, 136–142. [Google Scholar] [CrossRef]
- Bailin, H.; Zheng, W.M. Applied Symbolic Dynamics and Chaos; World Scientific: Singapore, 1998. [Google Scholar]
- Robinson, C. Dynamical Systems: Stability, Symbolic Dynamics, and Chaos; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Kitchens, B.P. Symbolic Dynamics: One-Sided, Two-Sided and Countable State Markov Shifts; Springer Science & Business Media: Heidelberg, NY, USA, 1998. [Google Scholar]
- Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Shaw, R. Strange attractors, chaotic behavior, and information flow. Z. Naturforsch. A 1981, 36, 80–112. [Google Scholar] [CrossRef]
- Barker, R.H. Group synchronizing of binary digital systems. In Communication Theory: Papers Read at a Symposium on Applications of Communication Theory Held at the Institution of Electrical Engineers, London, UK, 22–26 September 1952; Jackson, W., Ed.; Academic Press: New York, NY, USA, 1953; pp. 273–287. [Google Scholar]
- Hoskins, P.R.; Kevin, M.; Thrush, A. Diagnostic Ultrasound: Physics and Equipment; CRC Press/Taylor & Francis Group: Boca Raton, FL, USA, 2010. [Google Scholar]
- Haykin, S. Communication Systems; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Ren, H.P.; Bai, C.; Liu, J.; Baptista, M.S.; Grebogi, C. Experimental validation of wireless communication with chaos. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 083117. [Google Scholar] [CrossRef]
- Werner, F.T.; Rhea, B.K.; Harrison, R.C.; Dean, R.N. Electronic implementation of a practical matched filter for a chaos-based communication system. Chaos Solitons Fractals 2017, 104, 461–467. [Google Scholar] [CrossRef]
- Beal, A.N.; Blakely, J.N.; Corron, N.J.; Dean, R.N. High frequency oscillators for chaotic radar. Proc. SPIE 2016. [Google Scholar] [CrossRef]
- Beal, A.N.; Blakely, J.N.; Corron, N.J. Extended-bandwidth negative impedance converters by nested networks. IEEE Trans. Circuits Syst. Express Briefs 2018, 65, 1134–1138. [Google Scholar] [CrossRef]
- Fendley, C. CMOS Exactly Solvable Chaotic Oscillator. Master’s Thesis, Auburn University, Auburn, AL, USA, 18 November 2019. [Google Scholar]
- Chen, J.; Zhang, X.; Peng, J. Time-delayed chaotic circuit design using all-pass filter. IEEE Trans. Circuits Syst. Regul. Pap. 2014, 61, 2897–2903. [Google Scholar] [CrossRef]
- Charvat, G.L. Small and Short-Range Radar Systems; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Sang-Dong, K.; Lee, J.H. Performance analysis of UWB radar for vehicle in multi-user environments. In Proceedings of the 10th International Conference on Advanced Communication Technology, Gangwon-Do, South Korea, 17–20 February 2008. [Google Scholar]
- Thayaparan, T.; Daković, M.; Stanković, L. Mutual interference and low probability of interception capabilities of noise radar. IET Radar Sonar Navig. 2008, 2, 294–305. [Google Scholar] [CrossRef]
- Surender, S.C.; Narayanan, R.M.; Das, C.R. Performance analysis of communications & radar coexistence in a covert UWB OSA system. In Proceedings of the IEEE Global Telecommunications Conference GLOBECOM, Miami, FL, USA, 6 December 2010. [Google Scholar]
- Qiao, S.; Shi, Z.G.; Jiang, T.; Ran, L.X. A new architecture of UWB radar utilizing microwave chaotic signals and chaos synchronization. Prog. Electromagnet. Res. 2007, 75, 225–237. [Google Scholar] [CrossRef]
- Beal, A.N.; Dean, R.N. A random stimulation source for evaluating MEMS devices using an exact solvable chaotic oscillator. In Proceedings of the Additional Conferences (Device Packaging, HiTEC, HiTEN, & CICMT), Fountain Hills, AZ, USA, 10–13 March 2014. [Google Scholar]
- Cohen, S.D.; Gauthier, D.J. A pseudo-matched filter for chaos. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 033148. [Google Scholar] [CrossRef] [PubMed]
- Tang, X.; Mandal, S. An Integrated Chaotic Transceiver for Spread-Spectrum Radar and Communications. In Proceedings of the IEEE 62nd International Midwest Symposium on Circuits and Systems (MWSCAS), Dallas, TX, USA, 4–7 August 2019. [Google Scholar]
- Miranda, J.; Cabral, J.; Wagner, S.R.; Fischer Pedersen, C.; Ravelo, B.; Memon, M.; Mathiesen, M. Open platform for seamless sensor support in healthcare for the Internet of Things. Sensors 2016, 16, 2089. [Google Scholar] [CrossRef]
- Miranda, J.; Memon, M.; Cabral, J.; Ravelo, B.; Wagner, S.R.; Pedersen, C.F.; Mathiesen, M.; Nielsen, C. Eye on patient care: Continuous health monitoring: design and implementation of a wireless platform for healthcare applications. IEEE Microwave Mag. 2017, 18, 83–94. [Google Scholar] [CrossRef]
- Chia, M.Y.W.; Leong, S.W.; Sim, C.K.; Chan, K.M. Through-wall UWB radar operating within FCC’s mask for sensing heart beat and breathing rate. In Proceedings of the European Microwave Conference, Paris, France, 4–6 October 2005. [Google Scholar]
- Massagram, W.; Lubecke, V.M.; Hst-Madsen, A.; Boric-Lubecke, O. Assessment of heart rate variability and respiratory sinus arrhythmia via Doppler radar. IEEE Trans. Microwave Theory Tech. 2009, 57, 2542–2549. [Google Scholar] [CrossRef]
- Li, J.; Liu, L.; Zeng, Z.; Liu, F. Advanced signal processing for vital sign extraction with applications in UWB radar detection of trapped victims in complex environments. IEEEJ. Sel. Top. Appl. Earth Observations Remote Sens. 2013, 7, 783–791. [Google Scholar] [CrossRef]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beal, A.N.; Cohen, S.D.; Syed, T.M. Generating and Detecting Solvable Chaos at Radio Frequencies with Consideration to Multi-User Ranging. Sensors 2020, 20, 774. https://doi.org/10.3390/s20030774
Beal AN, Cohen SD, Syed TM. Generating and Detecting Solvable Chaos at Radio Frequencies with Consideration to Multi-User Ranging. Sensors. 2020; 20(3):774. https://doi.org/10.3390/s20030774
Chicago/Turabian StyleBeal, Aubrey N., Seth D. Cohen, and Tamseel M. Syed. 2020. "Generating and Detecting Solvable Chaos at Radio Frequencies with Consideration to Multi-User Ranging" Sensors 20, no. 3: 774. https://doi.org/10.3390/s20030774
APA StyleBeal, A. N., Cohen, S. D., & Syed, T. M. (2020). Generating and Detecting Solvable Chaos at Radio Frequencies with Consideration to Multi-User Ranging. Sensors, 20(3), 774. https://doi.org/10.3390/s20030774



