Detection Principles of Temperature Compensated Oscillators with Reactance Influence on Piezoelectric Resonator
Abstract
1. Introduction
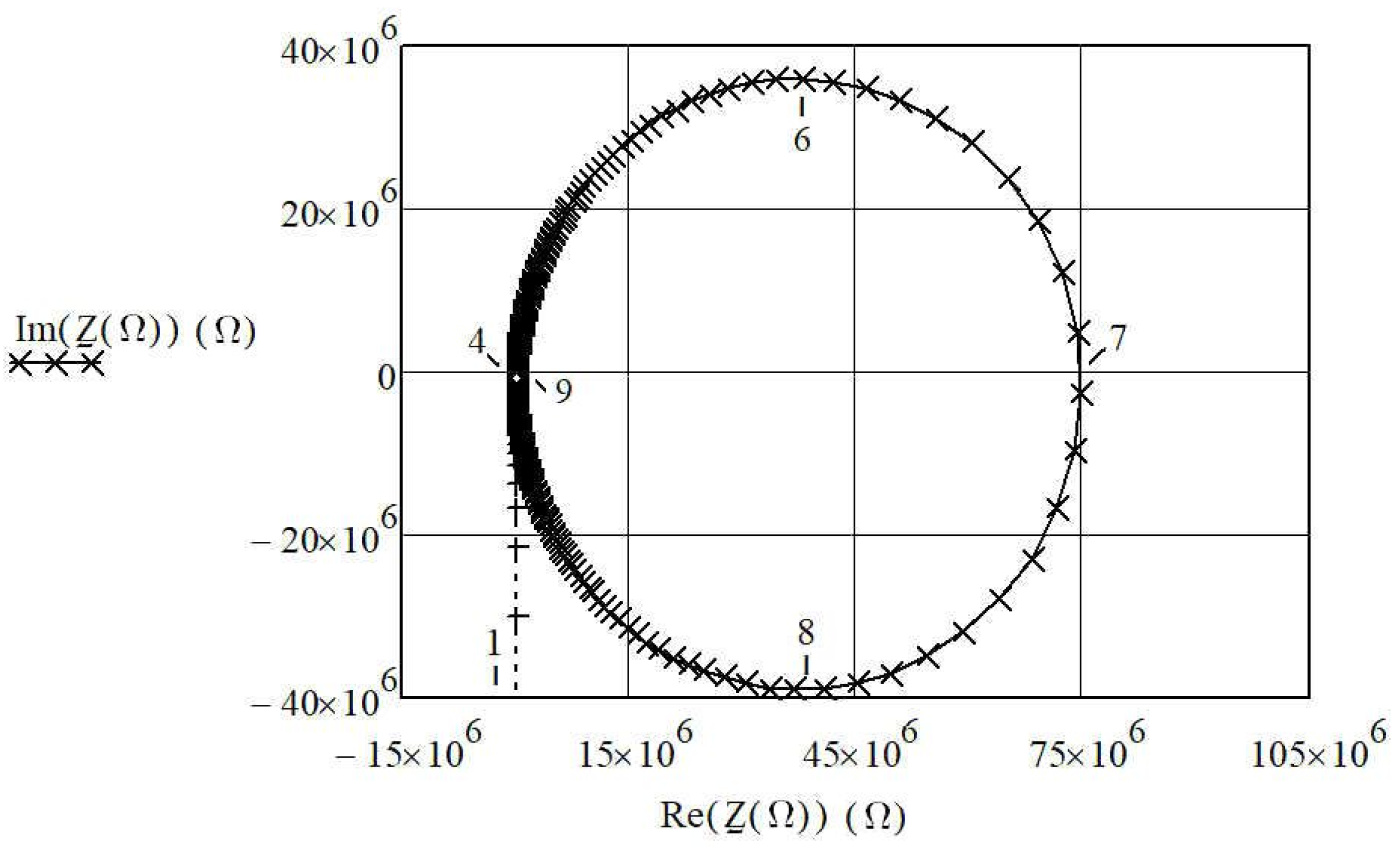
2. Piezoelectric Crystal Equivalent Circuit and its Impedance
3. Reactance Influence on Resonance of Piezoelectric Crystals
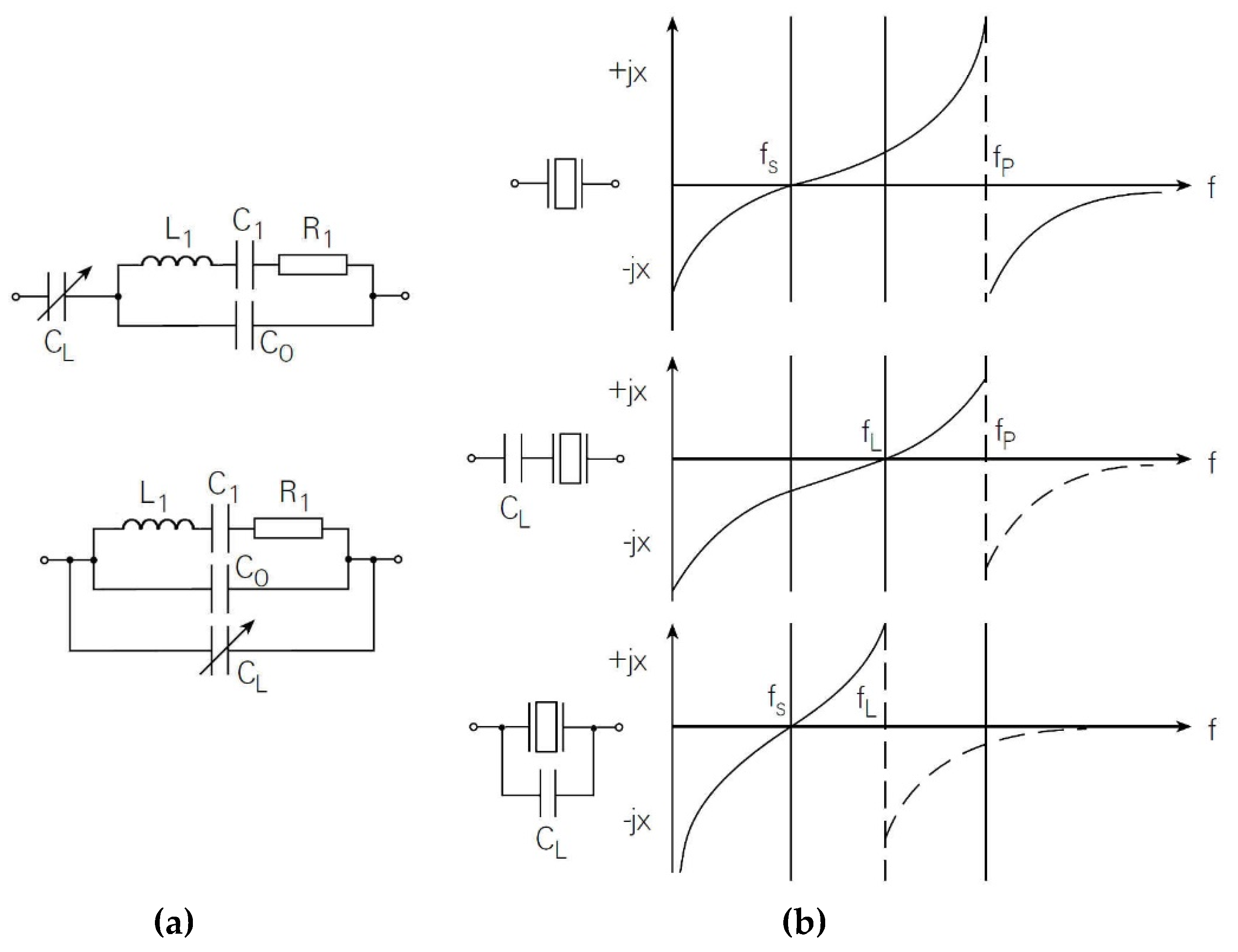
3.1. Load Capacitance Influence on Resonance
3.2. Capacitance Compensation of Piezoelectric Electrodes
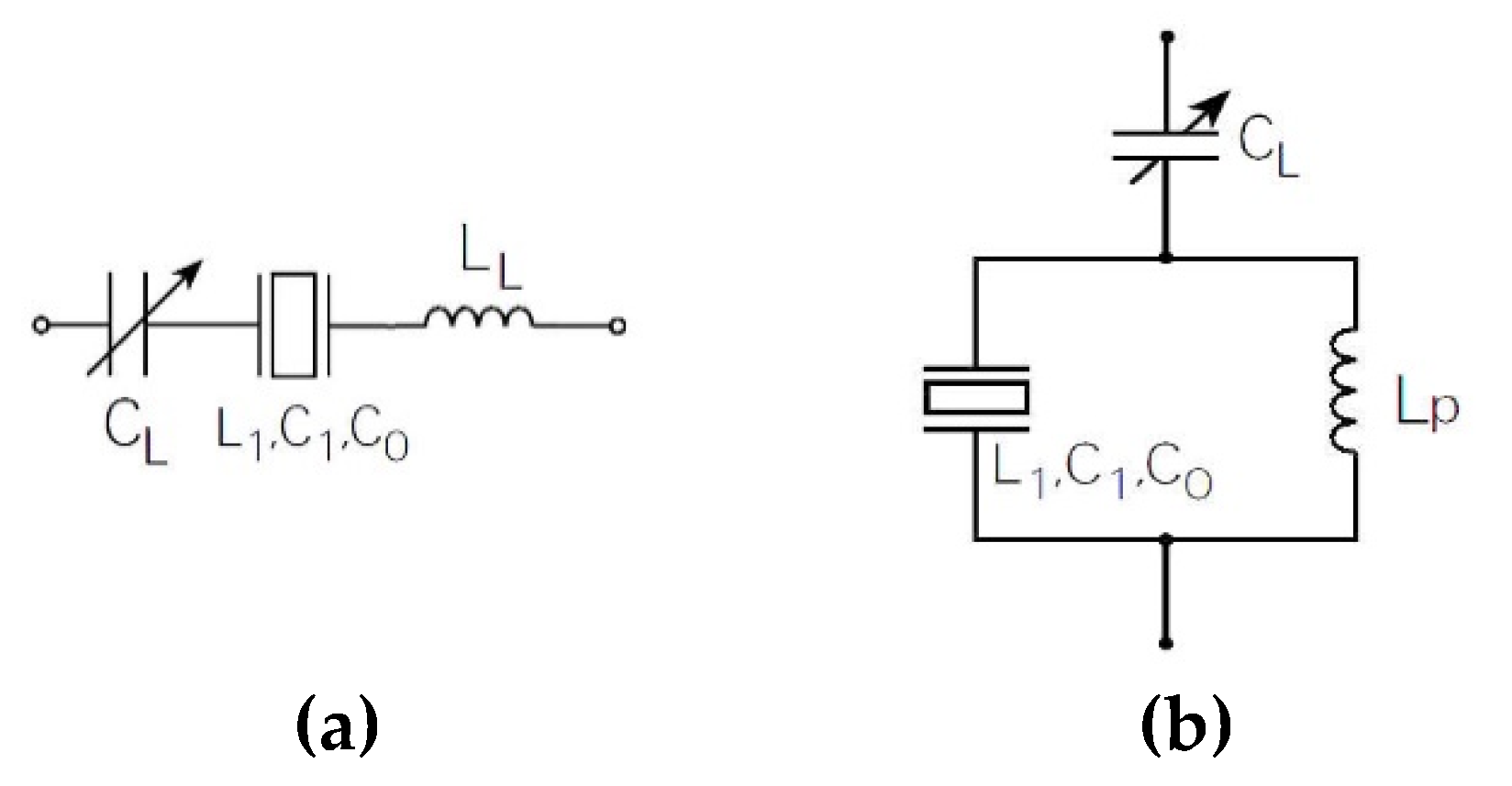
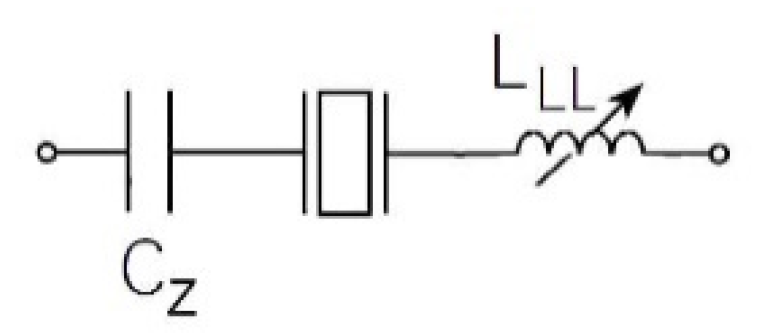
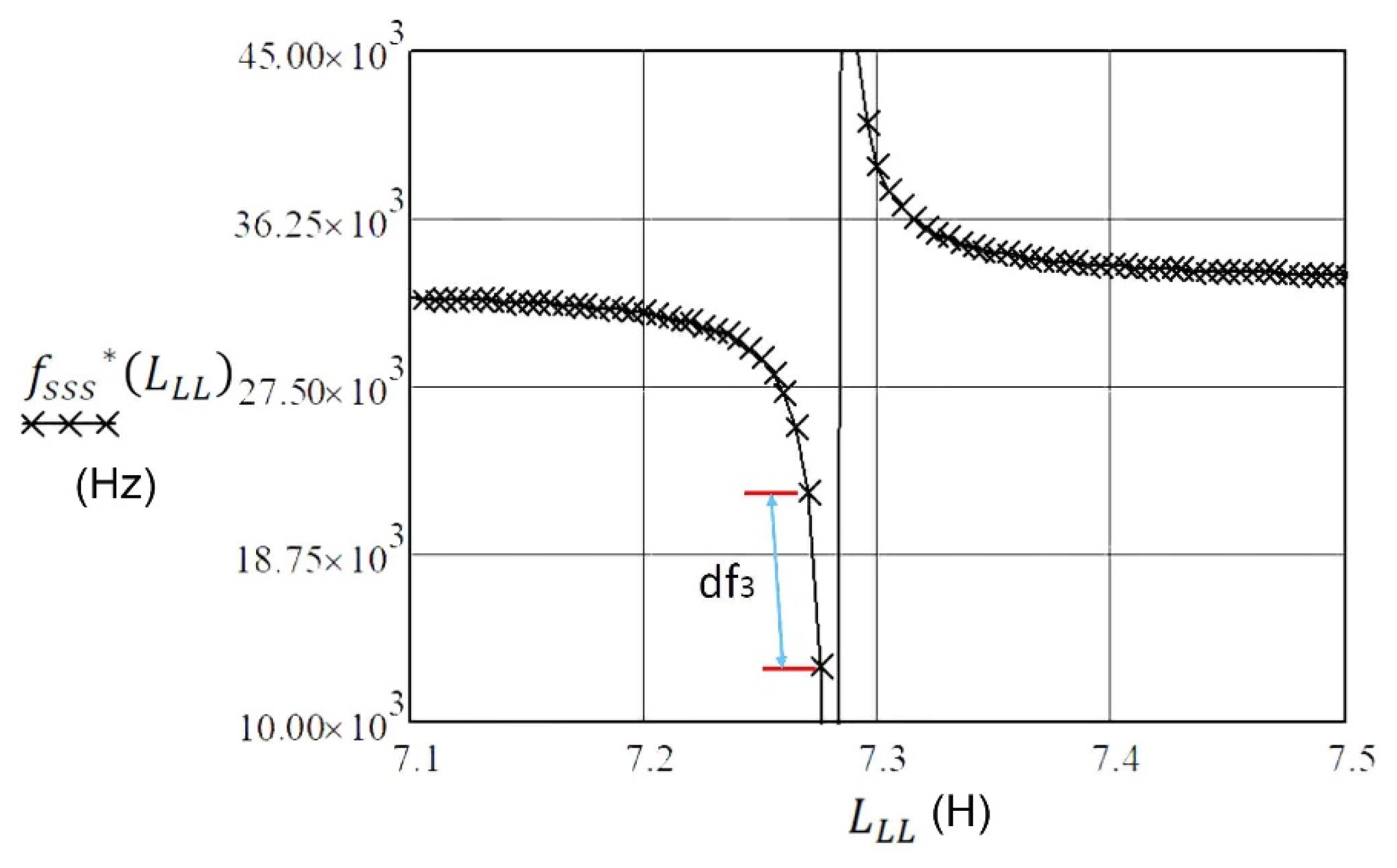
3.3. Load Inductance Influence on Resonance
3.4. Ceramic Resonators
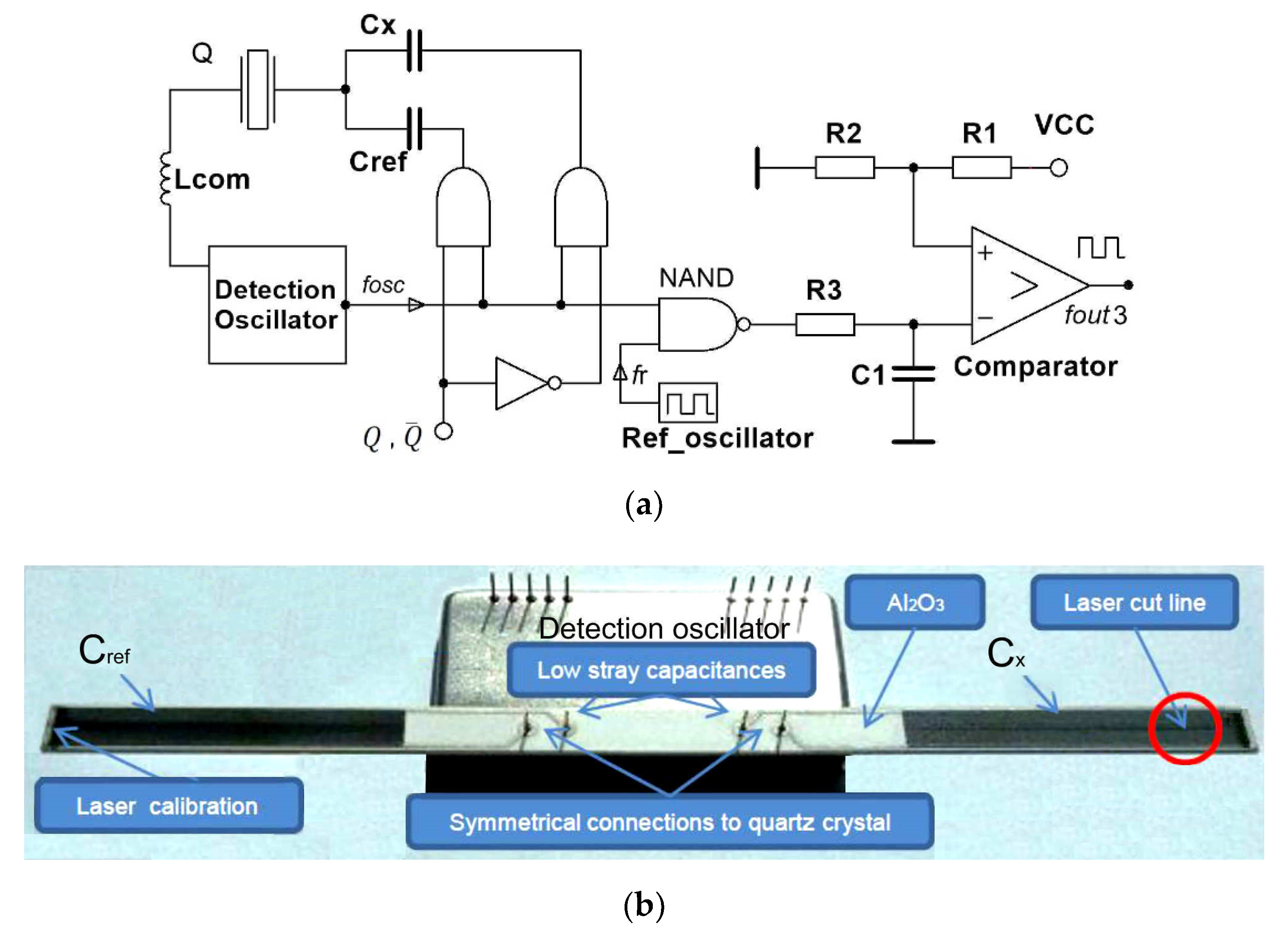
3.5. Oscillator Frequency Transformation Using Reference Oscillator
4. Temperature–Frequency Characteristics Compensation of Piezoelectric Crystals
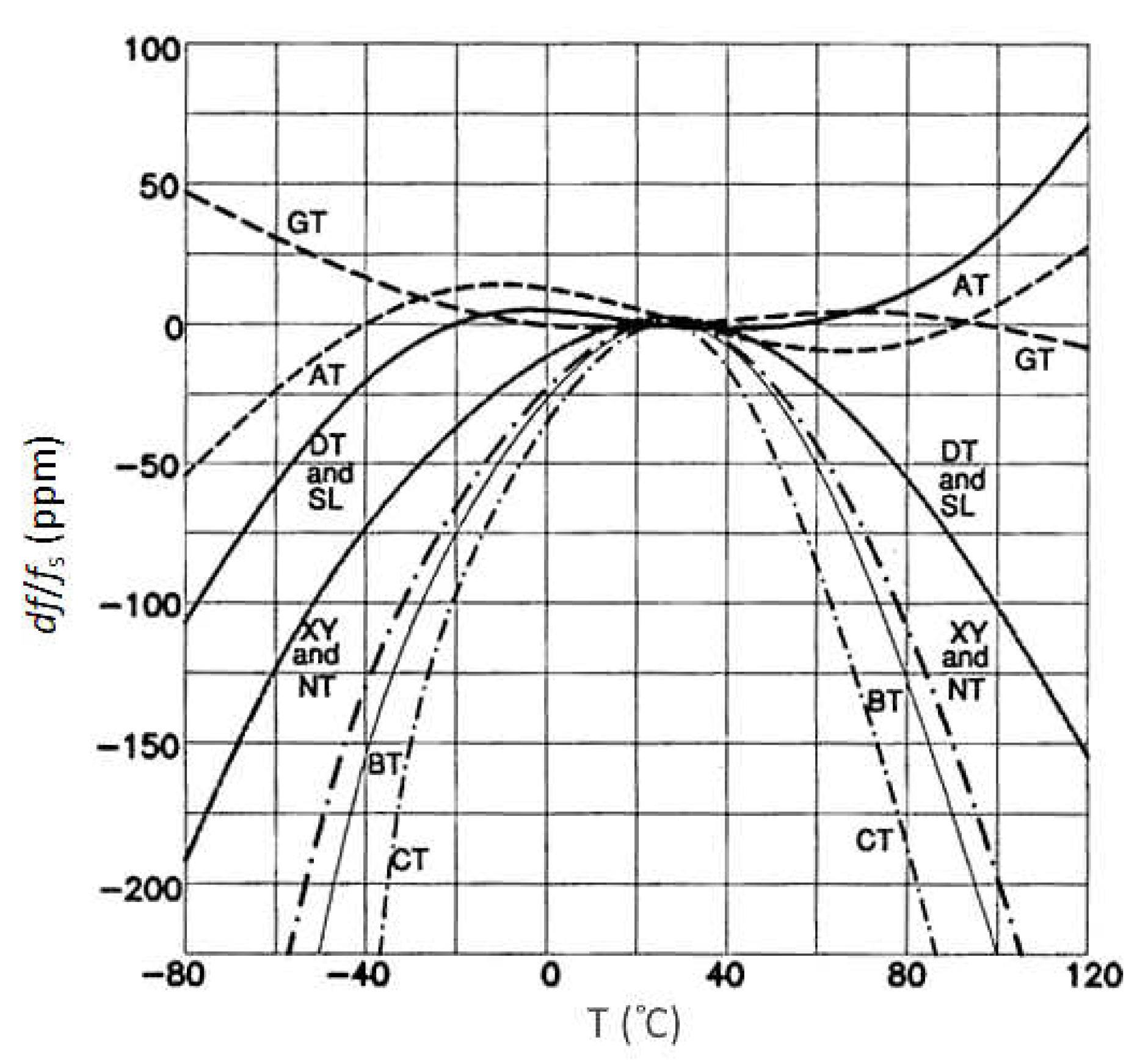
4.1. Crystal Temperature Sensitivity
4.2. Piezoelectric Crystal Temperature–Frequency Characteristics Compensation
4.2.1. Similar Crystal Temperature–Frequency Characteristics Compensation
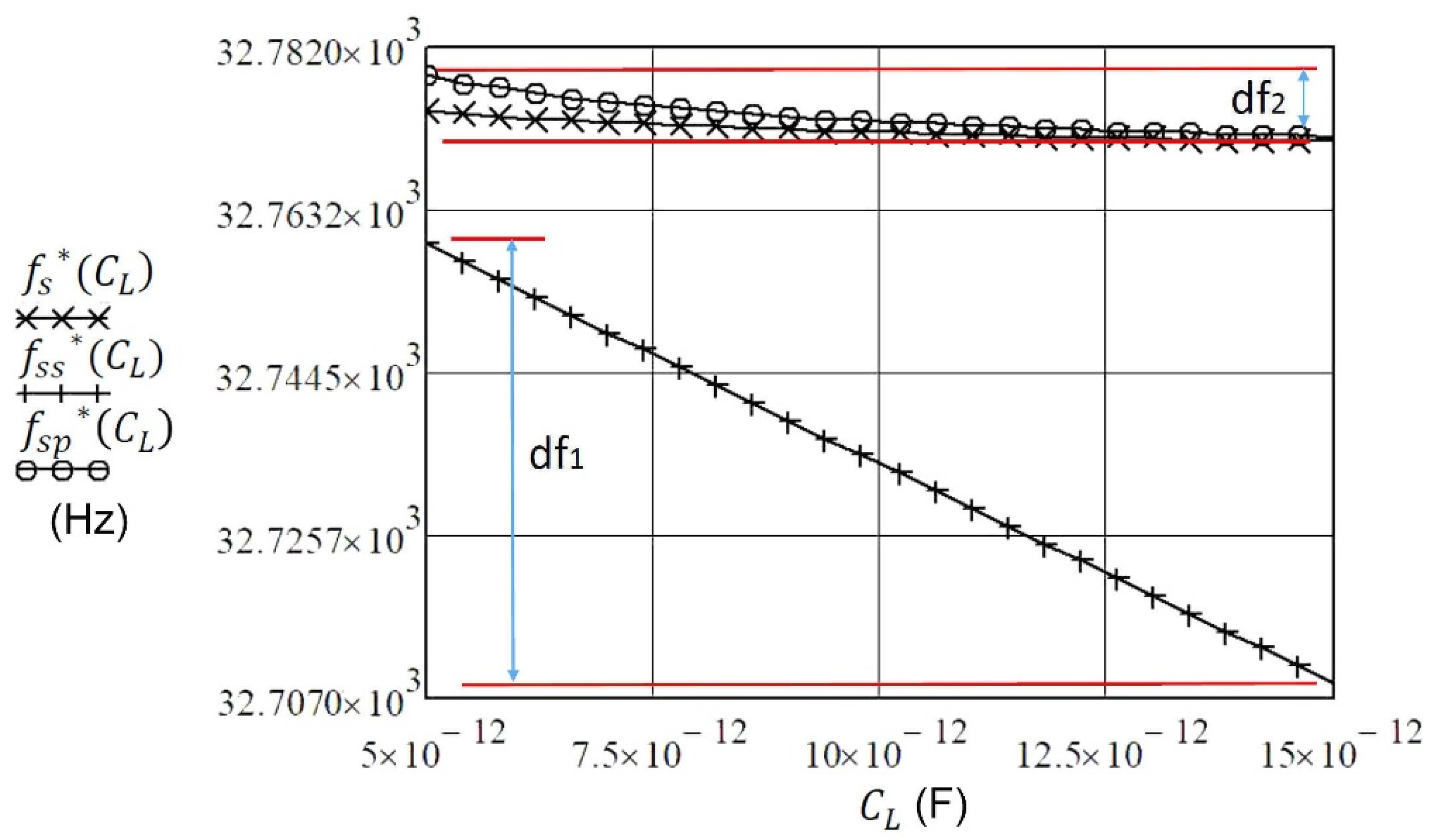
4.2.2. Crystal’s Temperature–Frequency Characteristics Compensation by Switching between the Load Capacitances
4.2.3. Crystal’s Own Temperature–Frequency Characteristics and Simultaneous Crystal Electrode Capacitance Compensation with one Inductance
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Euroquartz. Crystal Theory. Available online: https://euroquartz.co.uk/media/1879/tech-notes.pdf (accessed on 28 November 2019).
- Euroquartz. Oscillator Circuits. Available online: https://www.euroquartz.co.uk/media/1878/application-notes.pdf (accessed on 28 November 2019).
- Quartz Crystal Resonators and Oscillators for Frequency Control and Timing Applications. Available online: https://ieee-uffc.org/download/quartz-crystal-resonators-and-oscillators-for-frequency-control-and-timing-applications-a-tutorial-2/ (accessed on 28 November 2019).
- Nazemi, H.; Joseph, A.; Park, J.; Emadi, A. Advanced Micro- and Nano-Gas Sensor Technology: A Review. Sensors 2019, 19, 1285. [Google Scholar] [CrossRef] [PubMed]
- Wenjie, W.; Weihao, S.; Peter, T.; Mingsui, Y. Design and Analysis of Two Piezoelectric Cymbal Transducers with Metal Ring and Add Mass. Sensors 2019, 19, 137. [Google Scholar]
- Schrüfer, E. Electrical Measurement: Quartz as a Frequency Reference. Carl Hanser Verlag. München Wien. 1992, 2, 405–414. [Google Scholar]
- Valimaa, A.J.; Santos, J.T.; Ockeloen-Korppi, C.F.; Sillanpaa, M.A. Electrode configuration and electrical dissipation of mechanical energy in quartz crystal resonators. J. Micromech. Microeng. 2018, 28, 9. [Google Scholar] [CrossRef]
- Xie, J.; Hu, Y. Electric admittance analysis of quartz crystal resonator in thickness-shear mode induced by array of surface viscoelastic micro-beams. Appl. Math. Mech. 2017, 38, 29–38. [Google Scholar] [CrossRef]
- Li, X.; Lyu, D.; Song, Y.; Zhang, S.; Hu, P.; Jeong, H. Simultaneously Determining Sensitivity and Effective Geometrical Parameters of Ultrasonic Piezoelectric Transducers Using a Self-Reciprocity Method. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 1649–1657. [Google Scholar] [CrossRef]
- Xu, T.; Zhao, L.; Jiang, Z.; Guo, S.; Li, Z.; Luo, G.; Sun, L.; Zhang, L. An Analytical Equivalent Circuit Model for Optimization Design of a Broadband Piezoelectric Micromachined Ultrasonic Transducer with an Annular Diaphragm. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2019, 66, 1760–1776. [Google Scholar] [CrossRef]
- Qin, T.; Zjajo, A.; Berkelaarand, M.; van der Meijs, N. Considering Crosstalk Effects in Statistical Timing Analysis. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2014, 33, 318–322. [Google Scholar]
- Altammar, H.; Dhingra, A.; Salowitz, N. Initial study of internally embedded shear-mode piezoelectric transducers for the detection of joint defects in laminate structures. J. Intell. Mater. Syst. Struct. 2019, 30, 2314–2330. [Google Scholar] [CrossRef]
- Houguang, L.; Jinlei, C.; Jianhua, Y.; Zhushi, R.; Gang, C.; Shanguo, Y.; Xinsheng, H.; Mengli, W. Concept and Evaluation of a New Piezoelectric Transducer for an Implantable Middle Ear Hearing Device. Sensors 2017, 17, 2515. [Google Scholar]
- Saifullah, A.; Ronan, Z.; Bram, N. A Self-Oscillating Boosting Amplifier with Adaptive Soft Switching Control for Piezoelectric Transducers. IEEE J. Solid State Circuits 2019, 54, 253–265. [Google Scholar]
- Bandey, H.L.; Martin, S.J.; Cernosek, R.W.; Hillman, A.R. Modeling the Responses of Thichness-Shear Mode Resonators under Various Loading Conditions. Anal. Chem. 1999, 71, 2205–2214. [Google Scholar] [CrossRef] [PubMed]
- Matko, V. Next generation AT-cut quartz crystal sensing devices. Sensors 2011, 11, 4474–4482. [Google Scholar] [CrossRef] [PubMed]
- Vivek, R.T. A Review of Electric Impedance Matching Techniques for Piezoelectric Sensors, Actuators and Transducers. Electronics 2019, 8, 169. [Google Scholar]
- Statek. The Quartz Crystal Model and Its Frequencies. Technical Note 32. Available online: http://statek.com/wp-content/uploads/2018/03/tn32.pdf (accessed on 16 December 2019).
- Min-Chiang, C.; Zi-Neng, H.; Shih-Yung, P.; Wang, Z.; Lam, C.S. Modified BVD-Equivalent Circuit of FBAR by Taking Electrodes into Account; IEEE: Piscataway, NJ, USA, 2002; Volume 1, p. 973. [Google Scholar]
- Stanford. QCM100-Quartz Microbalance Theory and Calibration. Available online: http://www.thinksrs.com/downloads/PDFs/ApplicationNotes/QCMTheoryapp.pdf (accessed on 16 December 2019).
- Jauch. Quartz Crystal Theory. Measurement Methods. Pulling Sensitivity. Available online: https://www.jauch.com/downloadfile/5804d138f41b5_c3e35434e616a6a82bd5/quartz_crystal_theory_2007.pdf (accessed on 19 December 2019).
- Shuyu, L.; Jie, X. Effect of the Matching Circuit on the Electromechanical Characteristics of Sandwiched Piezoelectric Transducers. Sensors 2017, 17, 329. [Google Scholar]
- Na, W.S.; Beak, J. A Review of the Piezoelectric Electromechanical Impedance Based Structural Health Monitoring Technique for Engineering Structures. Sensors 2018, 18, 1307. [Google Scholar] [CrossRef]
- Budoya, D.; Bruno de, C.; Leandro, C.; Ricardo da, S.; Everaldo de, F.; Fabricio, B. Analysis of Piezoelectric Diaphragms in Impedance-Based Damage Detection in Large Structures. Proceedings 2017, 2, 131. [Google Scholar] [CrossRef]
- Matko, V. A Comparison of Frequency Pullability in Oscillators Using a Single AT-Cut Quartz Crystal and Those Using Two Single AT- Cut Crystals Connected in Parallel with a Series Load Capacitance or Series Load Inductance. Sensors 2006, 6, 746–755. [Google Scholar] [CrossRef]
- Matko, V.; Safaric, R. Major Improvements of Quartz Crystal Pulling Sensitivity and Linearity Using Series Reactance. Sensors 2009, 9, 8263–8270. [Google Scholar] [CrossRef]
- Erhart, J.; Sebastian, T. Effective Electromechanical Coupling for the Partially Electroded Ceramic Resonators of Different Geometries. Ann. Univ. Dunarea De Jos Galati: Fascicle Ixmetallurgy Mater. Sci. 2015, 33, 7–16. [Google Scholar]
- Karlash, V. Influence of Electric Loading Conditions on the Vibrations of Piezoceramic Resonators. Int. Appl. Mech. 2017, 53, 220. [Google Scholar] [CrossRef]
- Zaitsev, B.D.; Semyonov, A.P.; Teplykh, A.A.; Borodina, I.A. The sensor for measuring the micro-displacements based on the piezoelectric resonator with lateral electric field. Ultrasonics 2019, 99, 105973. [Google Scholar] [CrossRef]
- Williams, P. The Circuit Designer’s Companion, 4th ed.; Newnes: Amsterdam, The Netherlands, 2017; pp. 151–157. [Google Scholar]
- Arnau, A. A Review of Interface Electronic Systems for AT-cut Quartz Crystal Microbalance Applications in Liquids. Sensors 2008, 8, 370–411. [Google Scholar] [CrossRef] [PubMed]
- Walls, F.L.; Vig, J.R. Fundamental limits on the frequency stabilities of crystal oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 576. [Google Scholar] [CrossRef]
- Kusters, J.A.; Vig, J.R. Thermal hysteresis in quartz resonators-A review (frequency standards). In Proceedings of the 44th Annual Symposium on Frequency Control, Baltimore, MD, USA, 23–25 May 1990; pp. 165–175. [Google Scholar]
- Vig, J.R.; Filler, R.L. Temperature stable crystal oscillator. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 797. [Google Scholar] [CrossRef]
- Digital_Electronic_Siegfried. Quartz Crystals. Introduction and Guidance. Available online: https://www.digitallehrer.de/technische-einfuehrung-116179.html?language=en (accessed on 9 December 2019).
- Shao, J.; Yan, Z.; Han, S.; Li, H.; Gao, T.; Hu, X.; Wei, C. Differential signal extraction for continuous wave mud pulse telemetry. J. Pet. Sci. Eng. 2017, 148, 127–130. [Google Scholar] [CrossRef]
- Chen, C.; Yang, W.; Wang, J.; Lu, W.; Liu, X.; Jiang, X. Accurate and efficient height extraction in chromatic confocal microscopy using corrected fitting of the differential signal. Precis. Eng. 2019, 56, 447–454. [Google Scholar] [CrossRef]
- Bowick, C.; Ajluni, C.J.; Blyler, J. RF Circuit Design; Newnes: Amsterdam, The Netherlands, 2008; pp. 1–167. [Google Scholar]
- Bhattacharjee, S.; Sikder, N.; Singh, K.M. Ultrasonic Vibration Measurement based on FM demodulation in PLL Technique. In Proceedings of the 2019 2nd International Conference on Innovations in Electronics, Signal Processing and Communication (IESC), Shillong, India, 1–2 March 2019; pp. 232–237. [Google Scholar]
- Bradley, D.; Fear, M.; Fisher, S.; Guénault, A.; Haley, R.; Lawson, C.; Pickett, G.; Schanen, R.; Tsepelin, V.; Wheatland, L. Hysteresis, Switching and Anomalous Behaviour of a Quartz Tuning Fork in Superfluid He. J. Low Temp. Phys. 2014, 175, 379–384. [Google Scholar] [CrossRef][Green Version]
- Galagedera, S.K.K.; Flechsig, G.U. Deuterium Isotope Effects Upon the Redox-switching of the Viscosity of DNA Layers Observed by Electrochemical Quartz Crystal Micro-balance. Electroanalysis 2019, 31, 2074–2080. [Google Scholar] [CrossRef]







| fS | R1 | C1 | L1 | |
|---|---|---|---|---|
| Bending vibration | 1–50 kHz | 5–50 kΩ | 0.01 pF | 104 –103 H |
| Longitudinal vibration | 50–200 kHz | 2–5 kΩ | 0.10 pF | 10–100 H |
| Surface vibration | 150–800 kHz | 0.5–10 kΩ | 0.02 pF | 1–10 H |
| Thickness shear vibration | 0.5–20 MHz | 2–2000 Ω | 0.01 pF | 10–100 mH |
| fs_cer | |
|---|---|
| Longitudinal mode | 30 kHz–1 MHz |
| Area mode | 100 kHz–2 MHz |
| Thickness shear mode | 1 MHz–10 MHz |
| Expansion thickness mode | 2 MHz–100 MHz |
| Surface wave mode | 10 MHz–1 GHz |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matko, V.; Milanovič, M. Detection Principles of Temperature Compensated Oscillators with Reactance Influence on Piezoelectric Resonator. Sensors 2020, 20, 802. https://doi.org/10.3390/s20030802
Matko V, Milanovič M. Detection Principles of Temperature Compensated Oscillators with Reactance Influence on Piezoelectric Resonator. Sensors. 2020; 20(3):802. https://doi.org/10.3390/s20030802
Chicago/Turabian StyleMatko, Vojko, and Miro Milanovič. 2020. "Detection Principles of Temperature Compensated Oscillators with Reactance Influence on Piezoelectric Resonator" Sensors 20, no. 3: 802. https://doi.org/10.3390/s20030802
APA StyleMatko, V., & Milanovič, M. (2020). Detection Principles of Temperature Compensated Oscillators with Reactance Influence on Piezoelectric Resonator. Sensors, 20(3), 802. https://doi.org/10.3390/s20030802







