On the Achievable Capacity of MIMO-OFDM Systems in the CathLab Environment
Abstract
:1. Introduction
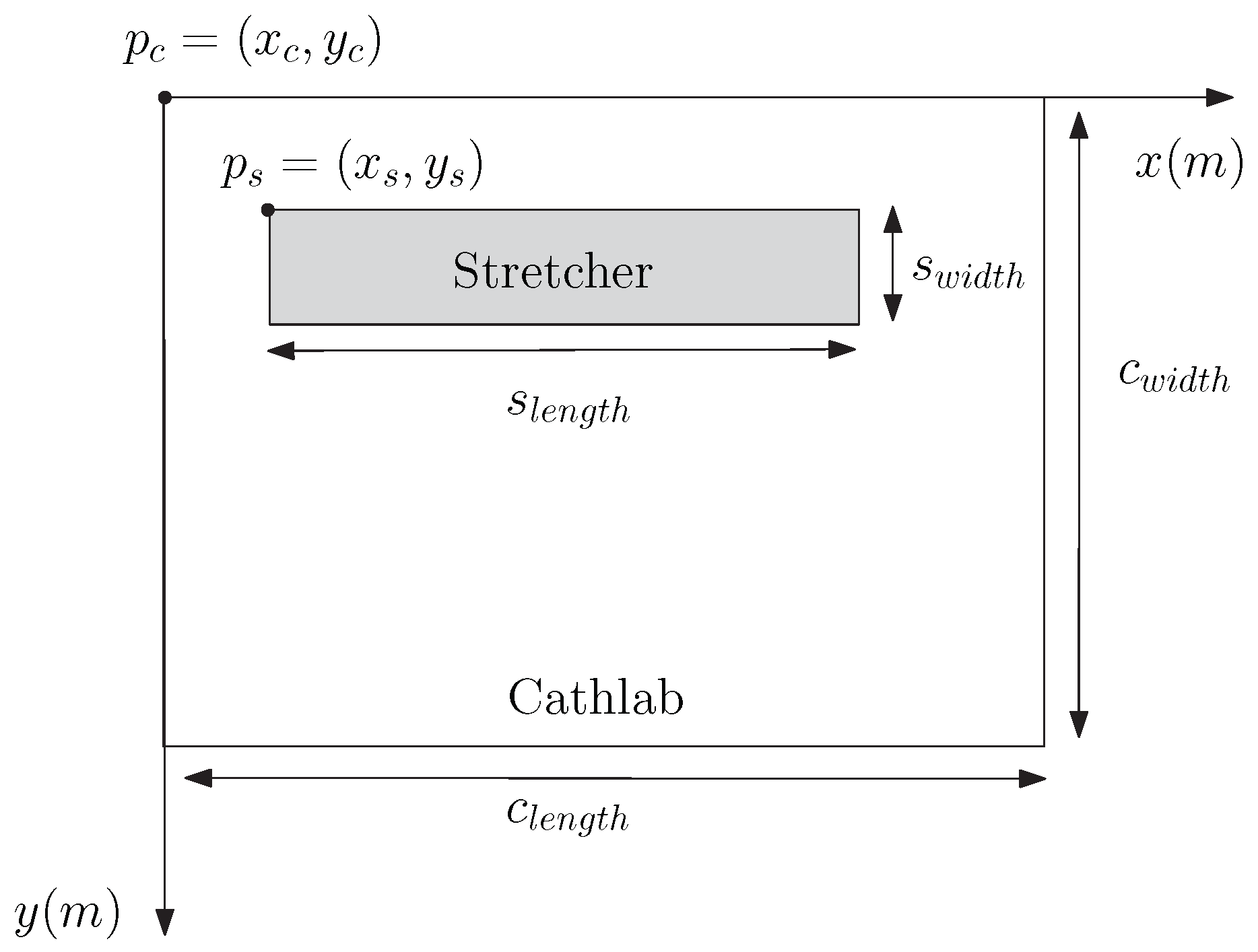
2. System Characterization
3. CathLab Channel
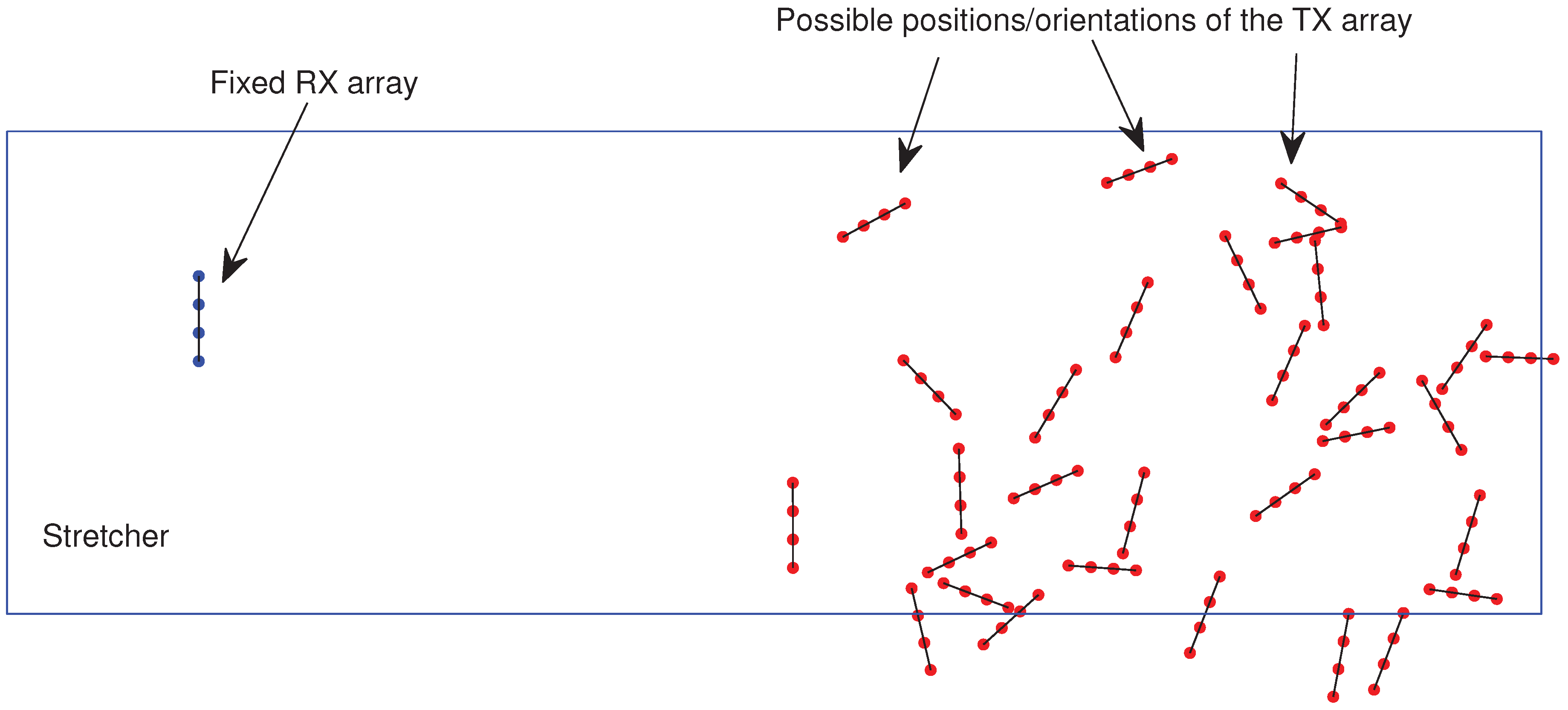
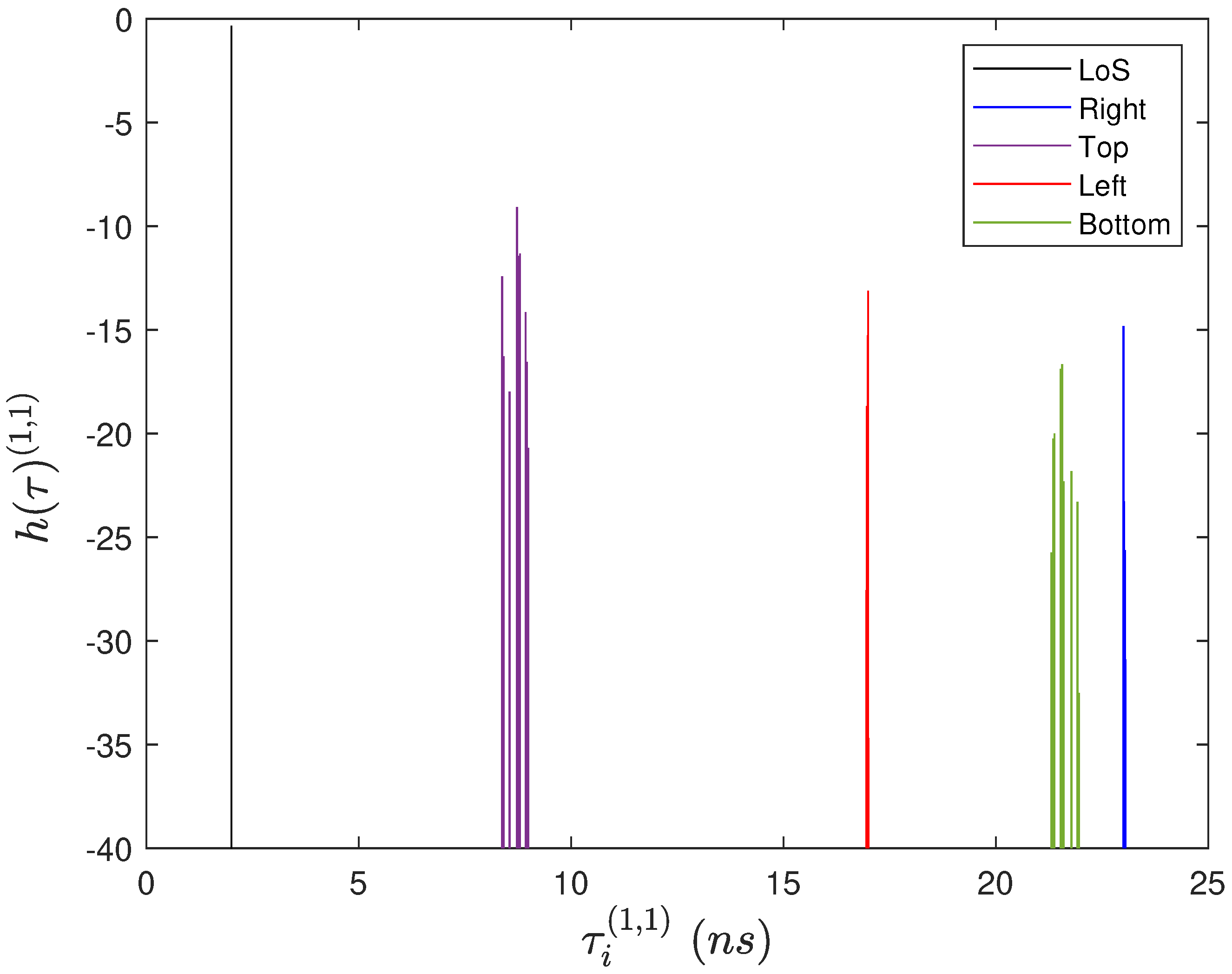
3.1. Ray-Tracing
3.2. CathLab-Based Channels
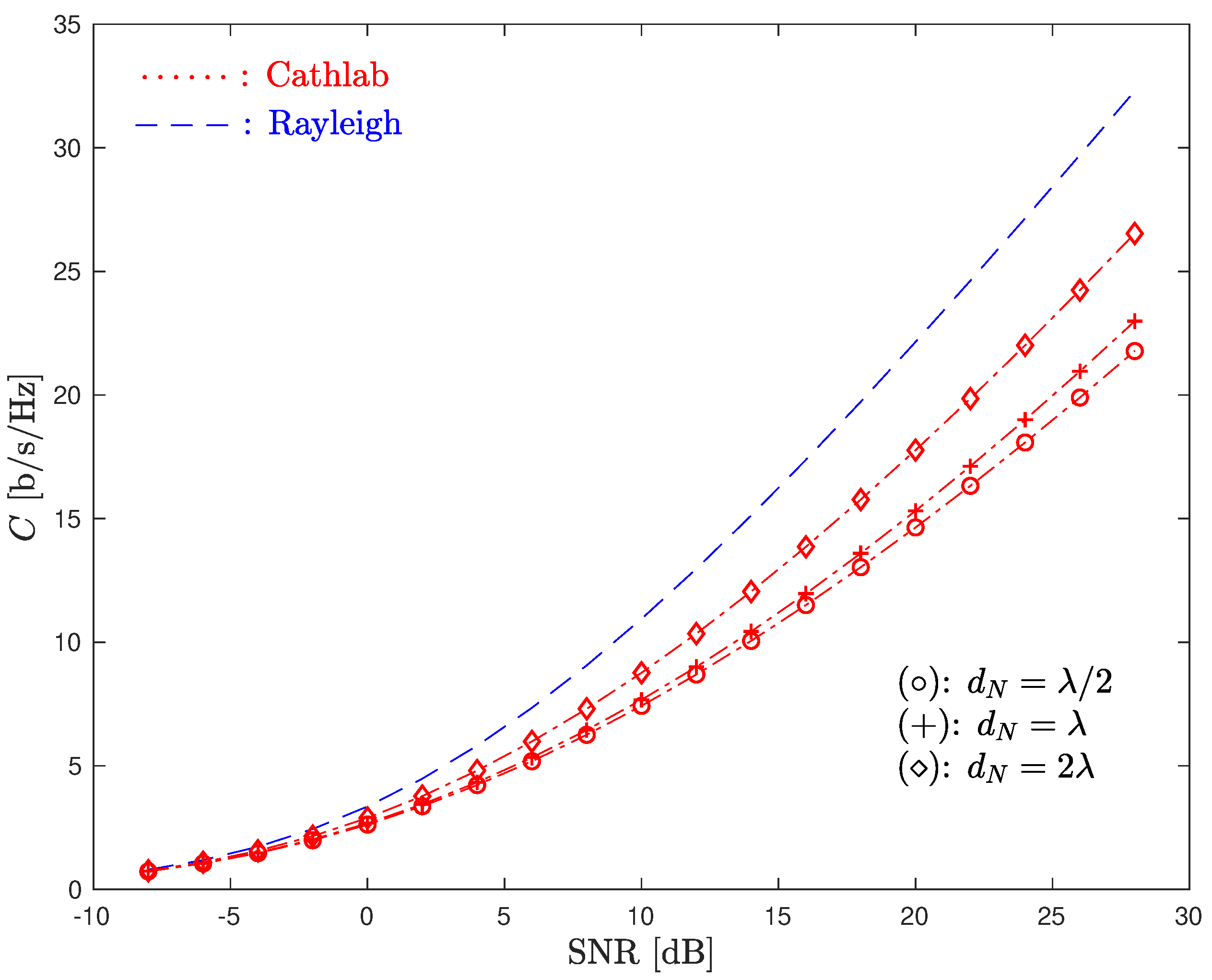
4. Channel Capacity
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Katouzian, A.; Angelini, E.D.; Carlier, S.G.; Suri, J.S.; Navab, N.; Laine, A.F. A state-of-the-art review on segmentation algorithms in intravascular ultrasound (IVUS) images. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 823–834. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, S.J.; Cho, N.; Kim, S.; Yoo, J.; Yoo, H.J. A 2Mb/s wideband pulse transceiver with direct-coupled interface for human body communications. In Proceedings of the IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 6–9 February 2006; pp. 2278–2287. [Google Scholar]
- Stoute, R.; Louwerse, M.C.; van Rens, J.; Henneken, V.A.; Dekker, R. Optical data link assembly for 360 μm diameter IVUS on guidewire imaging devices. In Proceedings of the SENSORS, 2014 IEEE, Valencia, Spain, 2–5 November 2014. [Google Scholar]
- Sharei, H.; Stoute, R.; van den Dobbelsteen, J.J.; Siebes, M.; Dankelman, J. Data communication pathway for sensing guidewire at proximal side: A review. J. Med. Devices 2017, 11, 024501. [Google Scholar] [CrossRef]
- Shobha, G.; Chittal, R.R.; Kumar, K. Medical applications of wireless networks. In Proceedings of the IEEE Second International Conference on Systems and Networks Communications (ICSNC 2007), Cap Esterel, France, 25–31 August 2007. [Google Scholar]
- Bellalta, B. IEEE 802.11ax: High-efficiency WLANs. IEEE Wirel. Commun. Mag. 2016, 23, 38–46. [Google Scholar] [CrossRef] [Green Version]
- Dianu, M.D.; Riihijärvi, J.; Petrova, M. Measurement-based study of the performance of IEEE 802.11 ac in an indoor environment. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014. [Google Scholar]
- Afaqui, M.S.; Garcia-Villegas, E.; Lopez-Aguilera, E. IEEE 802.11ax: Challenges and requirements for future high efficiency WiFi. IEEE Wirel. Commun. 2017, 24, 130–137. [Google Scholar] [CrossRef]
- Hanlen, L.; Grant, A. Capacity analysis of correlated MIMO channels. IEEE Trans. Inf. Theory 2012, 11, 6773–6787. [Google Scholar] [CrossRef]
- Foschini, G.J.; Gans, M.J. On limits of wireless communications in a fading environment when using multiple antennas. Wirel. Pers. Commun. 1998, 6, 311–335. [Google Scholar] [CrossRef]
- Goldsmith, A.; Jafar, S.A.; Jindal, N.; Vishwanath, S. Capacity limits of MIMO channels. IEEE J. Sel. Areas Commun. 2003, 21, 684–702. [Google Scholar] [CrossRef] [Green Version]
- Cimini, L. Analysis and simulation of a digital mobile channel using orthogonal frequency division multiplexing. IEEE Trans. Commun. 1985, 33, 665–675. [Google Scholar] [CrossRef] [Green Version]
- White Paper: The Wi-Fi Market and the Genesis of 802.11ax. Available online: https://www.arubanetworks.com/assets/wp/WP802.11AX.pdf (accessed on 5 February 2020).
- Khorov, E.; Kiryanov, A.; Lyakhov, A.; Bianchi, G. A tutorial on IEEE 802.11ax high efficiency WLANs. IEEE Commun. Surv. Tutor. 2019, 21, 197–216. [Google Scholar] [CrossRef]
- Yang, C.F.; Wu, B.C.; Ko, C.J. A ray-tracing method for modeling indoor wave propagation and penetration. IEEE Trans. Antennas Propag. 1998, 46, 907–919. [Google Scholar] [CrossRef]
- Dersch, U.; Zollinger, E. Propagation mechanisms in microcell and indoor environments. IEEE Trans. Veh. Technol. 1994, 43, 1058–1066. [Google Scholar] [CrossRef]
- Koppel, T.; Shishkin, A.; Haldre, H.; Toropovs, N.; Vilcane, I.; Tint, P. Reflection and transmission properties of common construction materials at 2.4 GHz Frequency. Energy Procedia 2017, 113, 158–165. [Google Scholar] [CrossRef]
- Telatar, E. Capacity of multi-antenna Gaussian channels. Eur. Trans. Telecommun. 1999, 10, 585–595. [Google Scholar] [CrossRef]







| MCS | Constellation | CR | R ( MHz) [Mbps] | R ( MHz) [Mbps] | R ( MHz) [Mbps] |
|---|---|---|---|---|---|
| 3 | 16-QAM | 1/2 | 68.8 | 144.1 | 288.2 |
| 5 | 64-QAM | 2/3 | 137.6 | 288.2 | 576.4 |
| 8 | 256-QAM | 3/4 | 206.5 | 434.2 | 868.4 |
| 10 | 1024-QAM | 3/4 | 258.1 | 540.4 | 1080.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerreiro, J.; Dinis, R.; Campos, L. On the Achievable Capacity of MIMO-OFDM Systems in the CathLab Environment. Sensors 2020, 20, 938. https://doi.org/10.3390/s20030938
Guerreiro J, Dinis R, Campos L. On the Achievable Capacity of MIMO-OFDM Systems in the CathLab Environment. Sensors. 2020; 20(3):938. https://doi.org/10.3390/s20030938
Chicago/Turabian StyleGuerreiro, João, Rui Dinis, and Luís Campos. 2020. "On the Achievable Capacity of MIMO-OFDM Systems in the CathLab Environment" Sensors 20, no. 3: 938. https://doi.org/10.3390/s20030938
APA StyleGuerreiro, J., Dinis, R., & Campos, L. (2020). On the Achievable Capacity of MIMO-OFDM Systems in the CathLab Environment. Sensors, 20(3), 938. https://doi.org/10.3390/s20030938






