3D Pose Estimation for Object Detection in Remote Sensing Images
Abstract
:1. Introduction
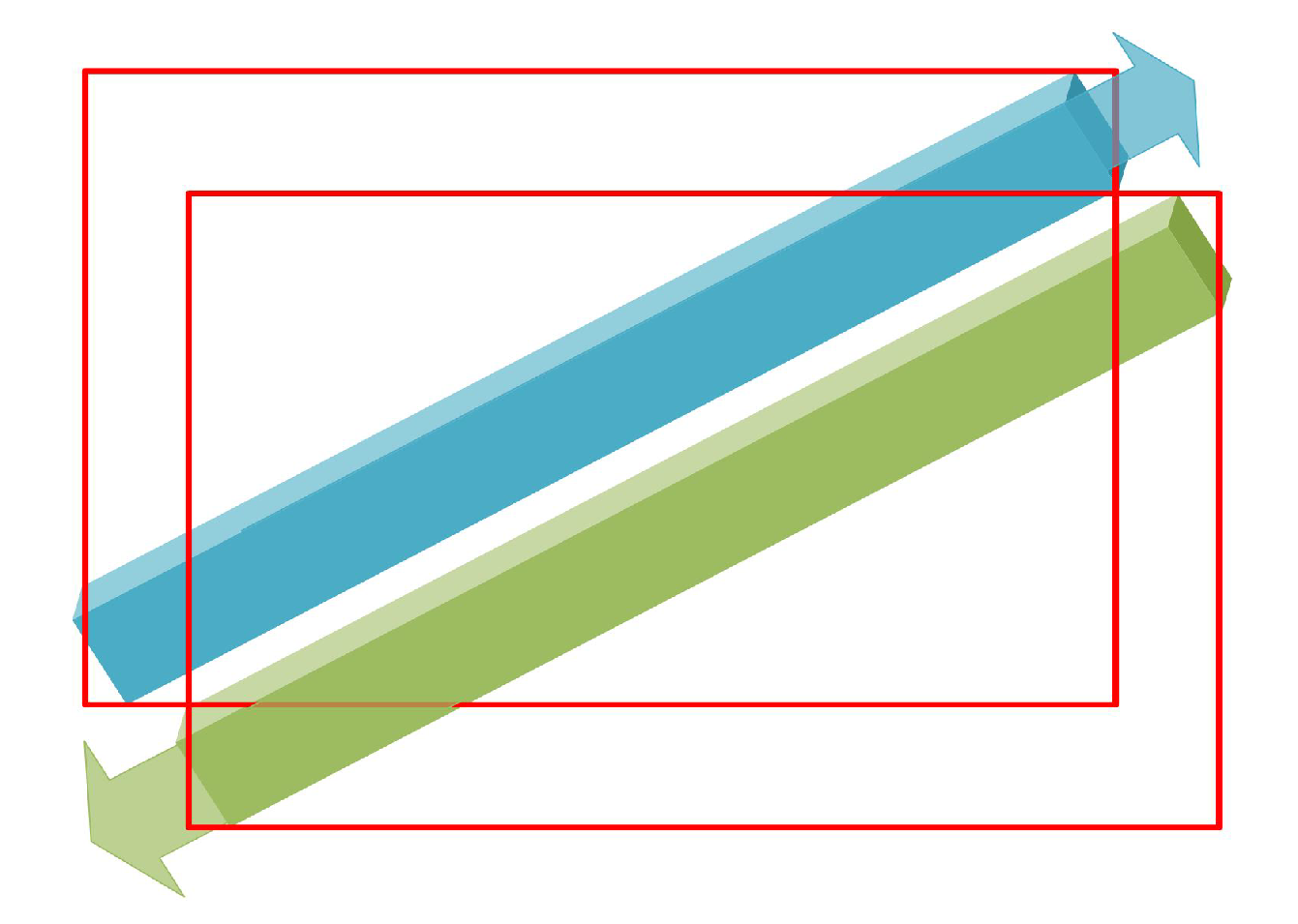
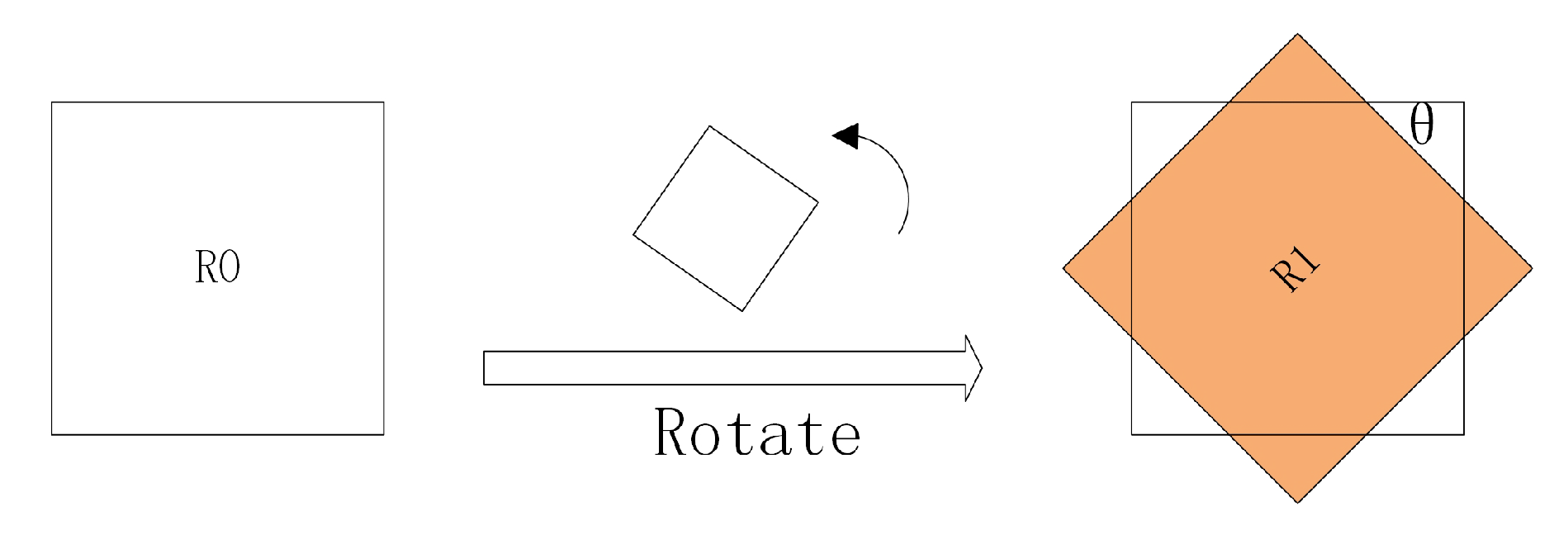
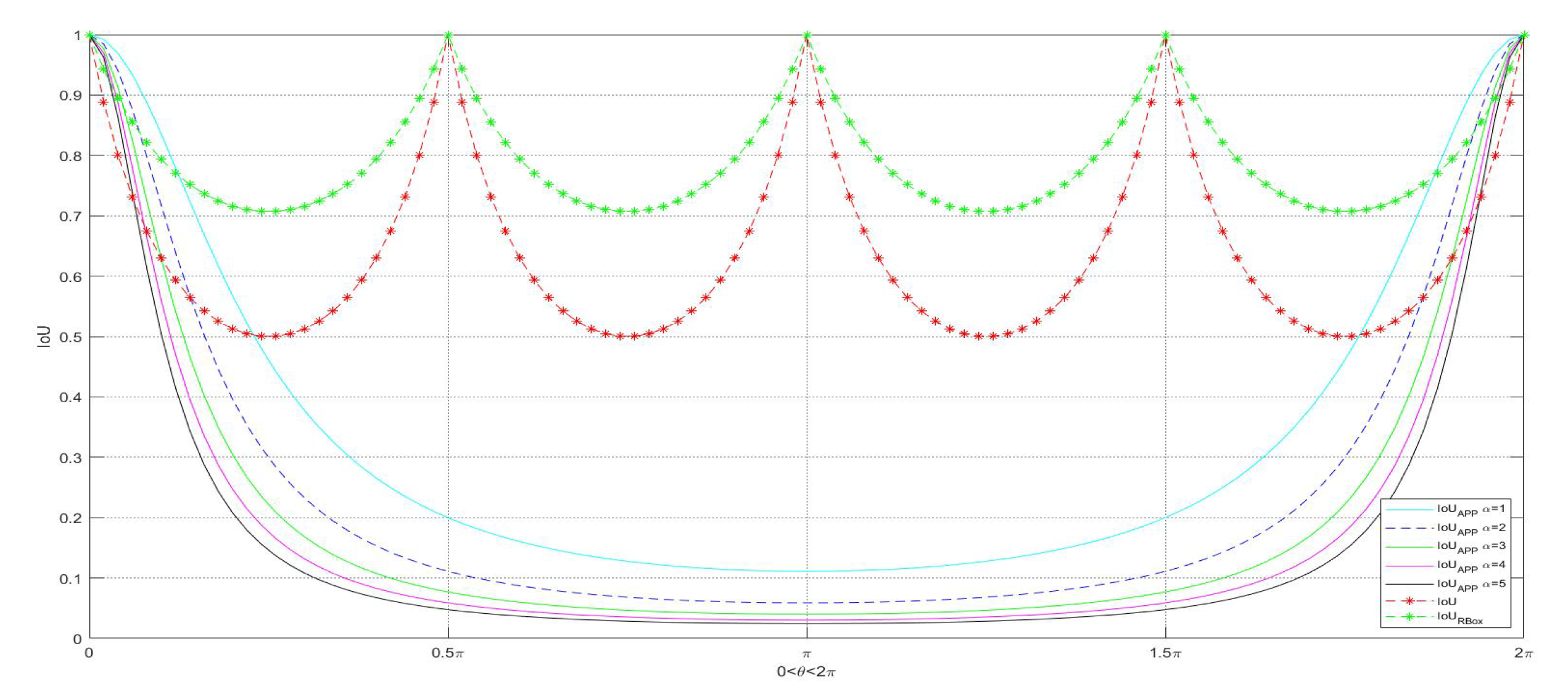
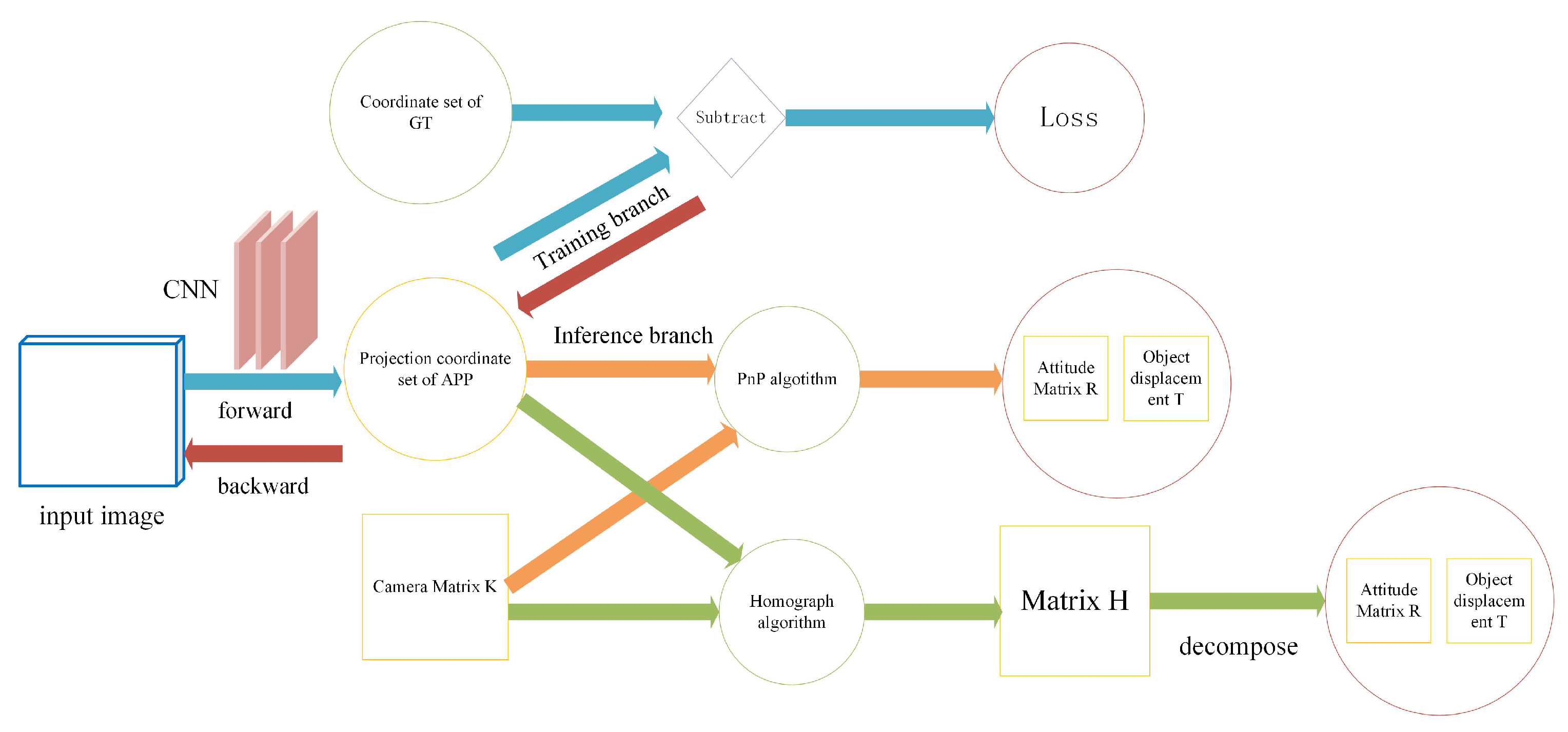
2. Object Detection Based on APP
3. Anchor Points Prediction Algorithm
3.1. Neural Network Design
3.2. Training Procedure
3.3. Calculation of the Object of 3D Pose
3.3.1. PnP Method
3.3.2. Homograph Method
- (1)
- Predict the APP coordinates of each object through the neural network.
- (2)
- According to Equation (15), we can get the inverse affine transformation parameters , , , and the object width-to-length ratio .
- (3)
- According to Equation (12), we can get the affine transformation matrix from the object coordinate system to the image coordinate system:
- (4)
- Matrix is obtained from Equation (17).
- (5)
- Attitude matrix R and displacement T can be obtained by decomposing matrix .
3.3.3. Object Spatial Location Using Remote Sensing Image
4. Experiments and Analysis
4.1. Experimental Details
4.2. Error Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Long, Y.; Gong, Y.; Xiao, Z.; Liu, Q. Accurate Object Localization in Remote Sensing Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2486–2498. [Google Scholar] [CrossRef]
- Wang, G.; Wang, X.; Fan, B.; Pan, C. Feature Extraction by Rotation-Invariant Matrix Representation for Object Detection in Aerial Image. IEEE Geosci. Remote Sens. Lett. 2017, 14, 851–855. [Google Scholar] [CrossRef]
- Deng, Z.; Sun, H.; Zhou, S.; Zhao, J.; Zou, H. Toward Fast and Accurate Vehicle Detection in Aerial Images Using Coupled Region-Based Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3652–3664. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 13–16 December 2015. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks; Curran Associates, Inc.: Montreal, QC, Canada, 2015; pp. 91–99. [Google Scholar]
- Cai, Z.; Vasconcelos, N. Cascade R-CNN: Delving Into High Quality Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake, UT, USA, 18–22 June 2018. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 24–27 June 2014. [Google Scholar]
- Ding, J.; Xue, N.; Long, Y.; Xia, G.S.; Lu, Q. Learning RoI Transformer for Oriented Object Detection in Aerial Images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Los Angeles, CA, USA, 16–19 June 2019. [Google Scholar]
- Ren, H.; El-Khamy, M.; Lee, J. CT-SRCNN: Cascade Trained and Trimmed Deep Convolutional Neural Networks for Image Super Resolution. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018; pp. 1423–1431. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.Y.; Dollar, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature Pyramid Networks for Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Etten, A.V. You Only Look Twice: Rapid Multi-Scale Object Detection In Satellite Imagery; Cornell University: Ithaca, NY, USA, 2018. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, Faster, Stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLOv3: An Incremental Improvement; Cornell University: Ithaca, NY, USA, 2018. [Google Scholar]
- Liu, Z.; Wang, H.; Weng, L.; Yang, Y. Ship Rotated Bounding Box Space for Ship Extraction From High-Resolution Optical Satellite Images With Complex Backgrounds. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1074–1078. [Google Scholar] [CrossRef]
- Liu, Z.; Hu, J.; Weng, L.; Yang, Y. Rotated region based CNN for ship detection. In Proceedings of the 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 18–20 September 2017; pp. 900–904. [Google Scholar] [CrossRef]
- Liu, K.; Mattyus, G. Fast Multiclass Vehicle Detection on Aerial Images. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1938–1942. [Google Scholar] [CrossRef] [Green Version]
- Law, H.; Deng, J. CornerNet: Detecting Objects as Paired Keypoints. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. In Advances in Neural Information Processing Systems 25; Pereira, F., Burges, C.J.C., Bottou, L., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Lake Tahoe, NV, USA, 2012; pp. 1097–1105. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition; Cornell University: Ithaca, NY, USA, 2014. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. SSD: Single Shot MultiBox Detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016. [Google Scholar]
- Zhou, X.; Wang, D.; Krähenbühl, P. Objects as Points; Cornell University: Ithaca, NY, USA, 2019. [Google Scholar]
- Rad, M.; Lepetit, V. BB8: A Scalable, Accurate, Robust to Partial Occlusion Method for Predicting the 3D Poses of Challenging Objects Without Using Depth. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You Only Look Once: Unified, Real-Time Object Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Zhang, K.; Zhang, Z.; Li, Z.; Qiao, Y. Joint Face Detection and Alignment Using Multitask Cascaded Convolutional Networks. IEEE Signal Proce. Lett. 2016, 23, 1499–1503. [Google Scholar] [CrossRef] [Green Version]
- Cao, Z.; Simon, T.; Wei, S.E.; Sheikh, Y. Realtime Multi-Person 2D Pose Estimation Using Part Affinity Fields. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Neubeck, A.; Van Gool, L. Efficient Non-Maximum Suppression. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR’06), Hong Kong, China, 20–24 August 2006; pp. 850–855. [Google Scholar] [CrossRef]
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The Pascal Visual Object Classes (VOC) Challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, G.; Ji, X.; Xiang, Y.; Fox, D. DeepIM: Deep Iterative Matching for 6D Pose Estimation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Liu, J.; He, S. 6D Object Pose Estimation without PnP; Cornell University: Ithaca, NY, USA, 2019. [Google Scholar]
- Zhang, Z.; Guo, W.; Zhu, S.; Yu, W. Toward Arbitrary-Oriented Ship Detection With Rotated Region Proposal and Discrimination Networks. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1745–1749. [Google Scholar] [CrossRef]
- Liao, M.; Zhu, Z.; Shi, B.; Xia, G.S.; Bai, X. Rotation-Sensitive Regression for Oriented Scene Text Detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake, UT, USA, 18–22 June 2018. [Google Scholar]
- Xia, G.S.; Bai, X.; Ding, J.; Zhu, Z.; Belongie, S.; Luo, J.; Datcu, M.; Pelillo, M.; Zhang, L. DOTA: A Large-Scale Dataset for Object Detection in Aerial Images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake, UT, USA, 18–22 June 2018. [Google Scholar]
- Ma, J.; Shao, W.; Ye, H.; Wang, L.; Wang, H.; Zheng, Y.; Xue, X. Arbitrary-Oriented Scene Text Detection via Rotation Proposals. IEEE Trans. Multimed. 2018, 20, 3111–3122. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.; Zhu, X.; Wang, X.; Yang, S.; Li, W.; Wang, H.; Fu, P.; Luo, Z. R2CNN: Rotational Region CNN for Orientation Robust Scene Text Detection; Cornell University: Ithaca, NY, USA, 2017. [Google Scholar]
- Kehl, W.; Manhardt, F.; Tombari, F.; Ilic, S.; Navab, N. SSD-6D: Making RGB-Based 3D Detection and 6D Pose Estimation Great Again. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]


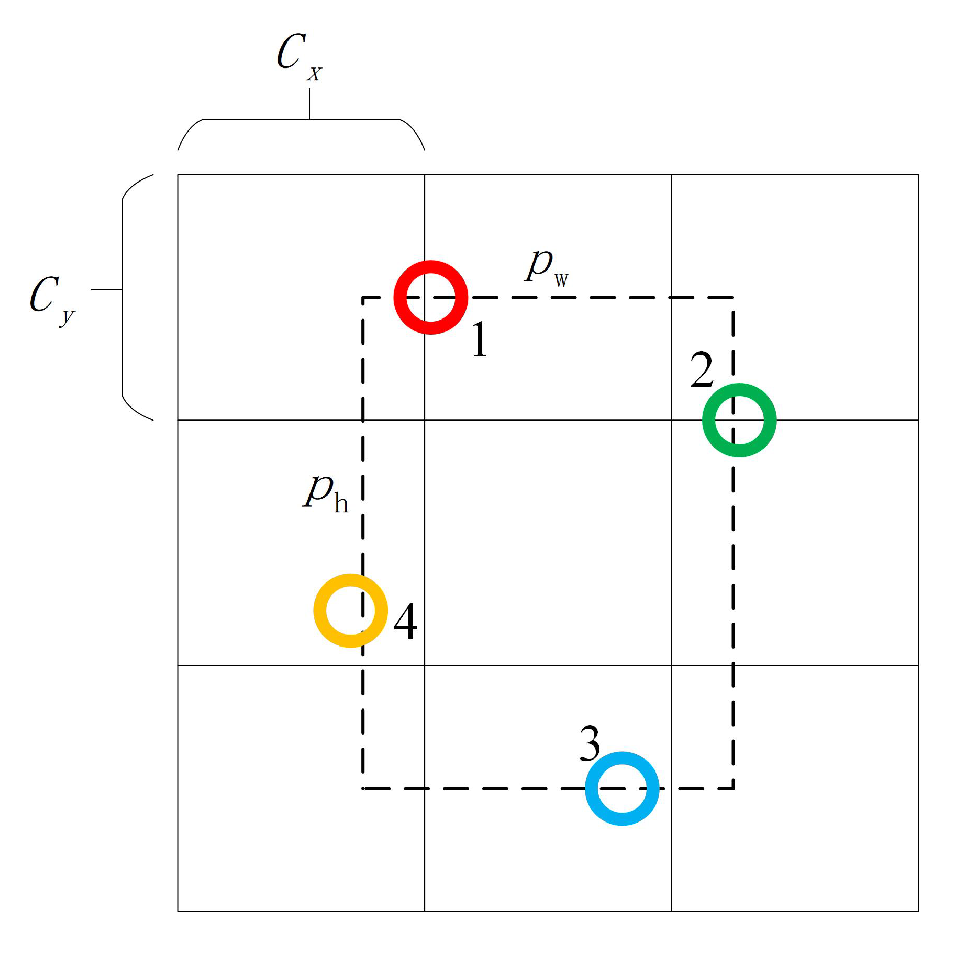




| Prediction Points | Object Information |
|---|---|
| 2 | RoI |
| 4 | inclined box |
| ≥4 | 3D pose |
| Parameter | 4 | n | 1 | c | |
|---|---|---|---|---|---|
| Description | bounding box coordinates | number of anchors | existing object | number of classes |
| Parameter | ||||||
|---|---|---|---|---|---|---|
| Description | loss weight of non-object | loss weight of object | loss weight of object RoI | loss weight of each point | predicted value of the point | ground truth of the point |
| Method | CP [15] | BL2 [15] | RC1 [15] | RC2 [15] | [31] | RRD [32] | RoI Trans. [8] | APP |
|---|---|---|---|---|---|---|---|---|
| mAP | 55.7 | 69.6 | 75.7 | 75.7 | 79.6 | 84.3 | 86.2 | 86.3 |
| Method | Plane | BD | Bridge | GTF | SV | LV | Ship | TC | BC | ST | SBF | RA | Harbor | SP | HC | mAP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FR-O [33] | 79.42 | 77.13 | 17.7 | 64.05 | 35.3 | 38.02 | 37.16 | 89.41 | 69.64 | 59.28 | 50.3 | 52.91 | 47.89 | 47.4 | 46.3 | 54.13 |
| RRPN [34] | 80.94 | 65.75 | 35.34 | 67.44 | 59.92 | 50.91 | 55.81 | 90.67 | 66.92 | 72.39 | 55.06 | 52.23 | 55.14 | 53.35 | 48.22 | 60.67 |
| R2CNN [35] | 88.52 | 71.2 | 31.66 | 59.3 | 51.85 | 56.19 | 57.25 | 90.81 | 72.84 | 67.38 | 56.69 | 52.84 | 53.08 | 51.94 | 53.58 | 61.01 |
| DPSRP [8] | 81.18 | 77.42 | 35.48 | 70.41 | 56.74 | 50.42 | 53.56 | 89.97 | 79.68 | 76.48 | 61.99 | 59.94 | 53.34 | 64.04 | 47.76 | 63.89 |
| RoI Trans. [8] | 88.53 | 77.91 | 37.63 | 74.08 | 66.53 | 62.97 | 66.57 | 90.5 | 79.46 | 76.75 | 59.04 | 56.73 | 62.54 | 61.29 | 55.56 | 67.74 |
| PnP | 87.98 | 75.38 | 45.93 | 71.26 | 65.10 | 68.93 | 77.04 | 87.63 | 81.59 | 78.96 | 58.54 | 57.20 | 63.95 | 62.32 | 49.01 | 68.72 |
| APP | 89.06 | 78.23 | 43.52 | 76.39 | 68.42 | 71.62 | 79.05 | 90.42 | 81.51 | 80.51 | 59.48 | 58.91 | 64.21 | 62.19 | 48.46 | 70.13 |
| Number | |||||
|---|---|---|---|---|---|
| 1 | 1 | 2 | 0.0001 | 1 | 1 |
| 2 | 1 | 3 | 0.0001 | 1 | 1 |
| 3 | 1 | 5 | 0.0001 | 2 | 1 |
| 4 | 1 | 2 | 0.0001 | 1.5 | 1 |
| 5 | 1 | 2 | 0.1 | 1 | 1 |
| Method | Plane | BD | Bridge | GTF | SV | LV | Ship | TC | BC | ST | SBF | RA | Harbor | SP | HC | mAP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 89.06 | 78.23 | 43.52 | 76.39 | 68.42 | 71.62 | 79.05 | 90.42 | 81.51 | 80.51 | 59.48 | 58.91 | 64.21 | 62.19 | 48.46 | 70.13 |
| 2 | 87.49 | 79.41 | 41.92 | 75.82 | 67.39 | 72.03 | 79.05 | 88.25 | 82.18 | 82.43 | 60.91 | 58.38 | 63.19 | 61.42 | 47.24 | 69.81 |
| 3 | 85.97 | 77.11 | 49.01 | 73.32 | 71.04 | 70.28 | 77.37 | 85.72 | 78.94 | 76.35 | 57.83 | 59.30 | 61.67 | 59.65 | 45.47 | 68.60 |
| 4 | 82.43 | 78.13 | 53.57 | 71.54 | 66.77 | 69.40 | 75.09 | 82.18 | 75.59 | 78.63 | 63.19 | 61.67 | 60.66 | 60.91 | 52.30 | 68.80 |
| 5 | 83.44 | 71.65 | 54.58 | 70.53 | 68.51 | 71.54 | 77.87 | 88.25 | 82.43 | 77.62 | 58.38 | 55.59 | 59.39 | 57.62 | 47.24 | 68.31 |
| Image Size | LR-O | RoI Trans. | DPSRP | APP |
|---|---|---|---|---|
| - | - | - | 13.5 | |
| 141 | 170 | 206 | 140 |
| Object | Plane | BD | Bridge | GTF | SV | LV | Ship | TC | BC | ST | SBF | RA | Harbor | SP | HC | avg |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| length | 1.04564 | 1.0169 | 1.7242 | 1.4834 | 2.1373 | 3.8274 | 2.9355 | 1.9410 | 1.8625 | 1.0174 | 1.3142 | 1.0278 | 4.4173 | 1.0914 | 2.9527 | 1.9863 |
| Number | Average Angle Error | Global Projection Pixel Error | |||||
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 0.0001 | 1 | 1 | 4.28 | 2.03 |
| 2 | 1 | 3 | 0.0001 | 1 | 1 | 4.32 | 2.05 |
| 3 | 1 | 5 | 0.0001 | 2 | 1 | 4.85 | 2.07 |
| 4 | 1 | 2 | 0.0001 | 1.5 | 1 | 4.93 | 2.16 |
| 5 | 1 | 2 | 0.1 | 1 | 1 | 4.78 | 2.37 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Gao, Y. 3D Pose Estimation for Object Detection in Remote Sensing Images. Sensors 2020, 20, 1240. https://doi.org/10.3390/s20051240
Liu J, Gao Y. 3D Pose Estimation for Object Detection in Remote Sensing Images. Sensors. 2020; 20(5):1240. https://doi.org/10.3390/s20051240
Chicago/Turabian StyleLiu, Jin, and Yongjian Gao. 2020. "3D Pose Estimation for Object Detection in Remote Sensing Images" Sensors 20, no. 5: 1240. https://doi.org/10.3390/s20051240
APA StyleLiu, J., & Gao, Y. (2020). 3D Pose Estimation for Object Detection in Remote Sensing Images. Sensors, 20(5), 1240. https://doi.org/10.3390/s20051240





