Designing a Streaming Algorithm for Outlier Detection in Data Mining—An Incrementa Approach †
Abstract
:1. Introduction
2. Related Works
2.1. Supervised Model
2.2. Semi-Supervised Model
2.3. Distance-Based Model
2.4. Density-Based Model
2.5. Probabilistic Model
2.6. Auto-Regressive Model
2.6.1. Deviation-Based Model
2.6.2. Kernel Density Model
2.7. Clustering-Based Model
2.8. Other Models
3. Algorithm C_KDE_WR
3.1. Density Estimation
3.1.1. Sliding Window Density Estimation
3.1.2. Binned Summary Density Estimation
3.2. Candidate Outliers and Retrospective
3.3. Binned Summary Maintenance
3.3.1. Calculate Bin Index
3.3.2. Update Bin Statistics
3.4. Complexity Analysis
4. Algorithm C_LOF
4.1. Local Outlier Factor
- For each data point p, compute its k-, i.e. the distance to its nearest neighbour.
- For each data point p, find its k-- of p, which contains every object q whose distance to p, noted as is not greater than k-.
- For each data point q in the k-- of p, calculate its reachability distance with respect to data record p as follows:
- For each data point p, calculate its local reachability density (lrd) of q as inverse of the average reachability distance over k-nearest neighbour of p:
- Finally, for each data point p, calculate its as ratio of average over k-nearest neighbour of p and of p itself
4.2. Incremental LOF
4.3. Update Operation
| Algorithm 1 Incremental LOF Update (Dataset S, Point ) |
|
4.4. Maintenance of Active Data Points
| Algorithm 2 Sliding Window Maintenance (Queue , Point ) |
|
4.5. Maintenance of Virtual Data Points
4.6. Complexity Analysis
5. Experiments and Results
5.1. Datasets
5.1.1. Synthetic Datasets
5.1.2. Real-World Datasets
5.2. Test Environment
5.3. Evaluation Criteria
5.4. Accuracy Evaluation for C_KDE_WR
5.5. Accuracy Evaluation for C_LOF
6. Conclusions and Future Works
- Though we managed to drop the number of false positives in C_KDE_WR, its number is still high in some specific cases. We believe that this number can be further reduced.
- The time complexity of C_LOF is still high, especially as dimension of data increases. Therefore, the result is more desirable when processing low-dimensional data. An efficient (or approximation) algorithm for clustering (based on reachability distances) is to be developed in order to decrease the overall complexity of C_LOF.
- Algorithms for detecting Type III outliers are barely found in the literature and therefore this area has much to be researched.
Author Contributions
Funding
Conflicts of Interest
References
- HewaNadungodage, C.; Xia, Y.; Lee, J. GPU-Accelerated Outlier Detection for Continuous Data Streams. In Proceedings of the 30th IEEE International Parallel and Distributed Processing Symposium (IPDPS), Chicago, IL, USA, 23–27 May 2016; pp. 1133–1142. [Google Scholar]
- Pokrajac, D.; Lazarevic, A.; Latecki, L. Incremental Local Outlier Detection for Data Streams. In Proceedings of the 1st IEEE Symposium on Computational Intelligence and Data Mining (CIDM), Honolulu, HI, USA, 1 March–5 April 2007; pp. 504–515. [Google Scholar]
- Sadik, S.; Gruenwald, L. Research Issues in Outlier Detection for Data Streams. SIGKDD Explor. Newsl. 2014, 15, 33–40. [Google Scholar] [CrossRef]
- Tatbul, N. Streaming data integration: Challenges and opportunities. In Proceedings of the 26th IEEE International Conference on Data Engineering Workshops (ICDEW), Long Beach, CA, USA, 1–6 March 2010; pp. 155–158. [Google Scholar] [CrossRef]
- Jiang, N.; Gruenwald, L. Research Issues in Data Stream Association Rule Mining. SIGMOD Rec. 2006, 35, 14–19. [Google Scholar] [CrossRef] [Green Version]
- Bremer, R. Outliers In Statistical Data. Technometrics 1995, 37, 117–118. [Google Scholar] [CrossRef]
- Cao, L.; Yang, D.; Wang, Q.; Yu, Y.; Wang, J.; Rundensteiner, E. Scalable distance-based outlier detection over high-volume data streams. In Proceedings of the 30th IEEE International Conference on Data Engineering (ICDE), Chicago, IL, USA, 31 March–4 April 2014; pp. 76–87. [Google Scholar]
- Georgiadis, D.; Kontaki, M.; Gounaris, A.; Papadopoulos, A.; Tsichlas, K.; Manolopoulos, Y. Continuous Outlier Detection in Data Streams: An Extensible Framework and State-of-the-art Algorithms. In Proceedings of the 38 International Conference on Management of Data (SIGMOD), New York, NY, USA, 22–27 June 2013; pp. 1061–1064. [Google Scholar] [CrossRef]
- Kontaki, M.; Gounaris, A.; Papadopoulos, A.; Tsichlas, K.; Manolopoulos, Y. Continuous monitoring of distance-based outliers over data streams. In Proceedings of the 27 IEEE International Conference on Data Engineering (ICDE), Hannover, Germany, 11–16 April 2011; pp. 135–146. [Google Scholar] [CrossRef]
- Knox, E.; Ng, R. Algorithms for mining distance-based outliers in large datasets. In Proceedings of the 24th International Conference on Very Large Databases (VLDB), New York City, NY, USA, 24–27 August 1998; pp. 392–403. [Google Scholar]
- Yu, K.; Shi, W.; Santoro, N.; Ma, X. Real-time Outlier Detection over Streaming Data. In Proceedings of the IEEE Smart World Congress (SWC 2019), Leicester, UK, 19–23 August 2019. [Google Scholar]
- Breunig, M.; Kriegel, H.; Ng, R.; Sander, J. LOF: Identifying Density-based Local Outliers. In Proceedings of the 25th International Conference on Management of Data (SIGMOD), Dallas, TX, USA, 16–18 May 2000; pp. 93–104. [Google Scholar] [CrossRef]
- Domingues, R.; Filippone, M.; Michiardi, P.; Zouaoui, J. A comparative evaluation of outlier detection algorithms: Experiments and analyses. Pattern Recognit. 2018, 74, 406–421. [Google Scholar] [CrossRef]
- Joshi, M.; Agarwal, R.; Kumar, V. Mining Needle in a Haystack: Classifying Rare Classes via Two-phase Rule Induction. SIGMOD Rec. 2001, 30, 91–102. [Google Scholar] [CrossRef]
- Chawla, N.; Lazarevic, A.; Hall, L.; Bowyer, K. SMOTEBoost: Improving the Prediction of Minority Class in Boosting. In Proceedings of the 7th Principles of Knowledge Discovery in Databases (PKDD), Cavtat-Dubrovnik, Croatia, 22–26 September 2003; pp. 107–119. [Google Scholar]
- Hawkins, S.; He, H.; Williams, G.; Baxter, R. Outlier Detection Using Replicator Neural Networks. In Proceedings of the 4th International Conference on Big Data Analytics and Knowledge Discovery (DaWaK), Provence, France, 4–6 September 2002; pp. 170–180. [Google Scholar]
- Wang, Q.; Luo, Z.; Huang, J.; Feng, Y.; Liu, Z. A novel ensemble method for imbalanced data learning: Bagging of extrapolation-SMOTE SVM. Comput. Intell. Neurosci. 2017, 2017, 1827016. [Google Scholar] [CrossRef] [PubMed]
- Hanifah, F.; Wijayanto, H.; Kurnia, A. SMOTEBagging Algorithm for Imbalanced Dataset in Logistic Regression Analysis (Case: Credit of Bank X). Appl. Math. Sci. 2015, 9, 6857–6865. [Google Scholar]
- Tantithamthavorn, C.; Hassan, A.; Matsumoto, K. The impact of class rebalancing techniques on the performance and interpretation of defect prediction models. arXiv 2018, arXiv:1801.10269. [Google Scholar] [CrossRef] [Green Version]
- Yap, B.; Rani, K.; Rahman, H.; Fong, S.; Khairudin, Z.; Abdullah, N. An application of oversampling, undersampling, bagging and boosting in handling imbalanced datasets. In Proceedings of the 1st International Conference on Advanced Data and Information Engineering (DaEng), Kuala Lumpur, Malaysia, 16–18 December 2013; pp. 13–22. [Google Scholar]
- Basu, S.; Bilenko, M.; Mooney, R. A Probabilistic Framework for Semi-supervised Clustering. In Proceedings of the 10th ACM International Conference on Knowledge Discovery and Data Mining (KDD), Seattle, WA, USA, 22–25 August 2004; pp. 59–68. [Google Scholar] [CrossRef]
- Wagstaff, K.; Cardie, C.; Rogers, S.; Schrödl, S. Constrained K-Means Clustering with Background Knowledge. In Proceedings of the 18th International Conference on Machine Learning (ICML), Williamstown, MA, USA, 28 June–1 July 2001; pp. 577–584. [Google Scholar]
- Yu, Y.; Guo, S.; Lan, S.; Ban, T. Anomaly intrusion detection for evolving data stream based on semi-supervised learning. In Proceedings of the 15th International Conference on Neural Information Processing (ICONIP), Auckland, New Zealand, 25–28 November 2008; pp. 571–578. [Google Scholar]
- Gao, J.; Cheng, H.; Tan, P. Semi-supervised Outlier Detection. In Proceedings of the 21st ACM Symposium on Applied Computing (SAC), Dijon, France, 23–27 April 2006; pp. 635–636. [Google Scholar] [CrossRef]
- Ramaswamy, S.; Rastogi, R.; Shim, K. Efficient Algorithms for Mining Outliers from Large Data Sets. In Proceedings of the 19th International Conference on Management of Data (SIGMOD), Dallas, TX, USA, 16–18 May 2000; pp. 427–438. [Google Scholar] [CrossRef]
- Angiulli, F.; Pizzuti, C. Outlier mining in large high-dimensional data sets. IEEE Trans. Knowl. Data Eng. 2005, 17, 203–215. [Google Scholar] [CrossRef] [Green Version]
- Tran, L.; Fan, L.; Shahabi, C. Distance-based Outlier Detection in Data Streams. Proc. VLDB Endow. 2016, 9, 1089–1100. [Google Scholar] [CrossRef] [Green Version]
- Sadik, S.; Gruenwald, L. DBOD-DS: Distance based outlier detection for data streams. In Proceedings of the 21st International Conference on Database and Expert Systems Applications (DEXA), Bilbao, Spain, 30 August–3 September 2010; pp. 122–136. [Google Scholar]
- Sadik, S.; Gruenwald, L. Online Outlier Detection for Data Streams. In Proceedings of the 15th Symposium on International Database Engineering & Applications Symposium (IDEAS), Lisboa, Portugal, 21–23 September 2011; pp. 88–96. [Google Scholar] [CrossRef]
- Sadik, S.; Gruenwald, L.; Leal, E. In pursuit of outliers in multi-dimensional data streams. In Proceedings of the 4th IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 5–8 December 2016; pp. 512–521. [Google Scholar] [CrossRef]
- Papadimitriou, S.; Kitagawa, H.; Gibbons, P.; Faloutsos, C. LOCI: Fast outlier detection using the local correlation integral. In Proceedings of the 19th International Conference on Data Engineering (ICDE), Bangalore, India, 5–8 March 2003; pp. 315–326. [Google Scholar]
- Sreevidya, S. A Survey on Outlier Detection Methods. Int. J. Comput. Sci. Inf. Technol. (IJCSIT) 2014, 5, 8153–8156. [Google Scholar]
- Yamanishi, K.; Takeuchi, J.; Williams, G.; Milne, P. On-line unsupervised outlier detection using finite mixtures with discounting learning algorithms. Data Min. Knowl. Discov. 2004, 8, 275–300. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B (Methodol.) 1977, 39, 1–22. [Google Scholar]
- Blei, D.M.; Jordan, M.I. Variational inference for Dirichlet process mixtures. Bayesian Anal. 2006, 1, 121–143. [Google Scholar] [CrossRef]
- Quinn, J.A.; Sugiyama, M. A least-squares approach to anomaly detection in static and sequential data. Pattern Recognit. Lett. 2014, 40, 36–40. [Google Scholar] [CrossRef]
- Curiac, D.; Banias, O.; Dragan, F.; Volosencu, C.; Dranga, O. Malicious Node Detection in Wireless Sensor Networks Using an Autoregression Technique. In Proceedings of the 3rd International Conference on Networking and Services (ICNS), Athens, Greece, 19–25 June 2007; p. 83. [Google Scholar] [CrossRef]
- Arning, A.; Agrawal, R.; Raghavan, P. A Linear Method for Deviation Detection in Large Databases. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining (KDD), Portland, OR, USA, 2–4 August 1996; pp. 164–169. [Google Scholar]
- Aggarwal, C.; Yu, P. Outlier detection for high dimensional data. In Proceedings of the 26th International Conference on Management of Data (SIGMOD), Santa Barbara, CA, USA, 21–24 May 2001; Volume 30, pp. 37–46. [Google Scholar]
- Scott, D. Multivariate Density Estimation: Theory, Practice, and Visualization; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Subramaniam, S.; Palpanas, T.; Papadopoulos, D.; Kalogeraki, V.; Gunopulos, D. Online Outlier Detection in Sensor Data Using Non-parametric Models. In Proceedings of the 32nd International Conference on Very Large Databases (VLDB), Seoul, Korea, 12–15 September 2006; pp. 187–198. [Google Scholar]
- Elahi, M.; Li, K.; Nisar, W.; Lv, X.; Wang, H. Efficient Clustering-Based Outlier Detection Algorithm for Dynamic Data Stream. In Proceedings of the 5th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Shandong, China, 18–20 October 2008; Volume 5, pp. 298–304. [Google Scholar] [CrossRef]
- Dhaliwal, P.; Bhatia, M.; Bansal, P. A cluster-based approach for outlier detection in dynamic data streams (KORM: K-median OutlieR miner). arXiv 2010, arXiv:1002.4003. [Google Scholar]
- Schölkopf, B.; Williamson, R.C.; Smola, A.J.; Shawe-Taylor, J.; Platt, J.C. Support vector method for novelty detection. In Advances in Neural Information Processing Systems; The MIT Press: Cambridge, MA, USA, 2000; pp. 582–588. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.H. Isolation forest. In Proceedings of the 2008 Eighth IEEE International Conference on Data Mining, Pisa, Italy, 15–19 December 2008; pp. 413–422. [Google Scholar]
- Fan, J.; Marron, J. Fast Implementations of Nonparametric Curve Estimators. J. Comput. Graph. Stat. 1994, 3, 35–56. [Google Scholar] [CrossRef]
- Brailsford, T.; Penm, J.; Terrell, R. Selecting the forgetting factor in subset autoregressive modelling. J. Time Ser. Anal. 2002, 23, 629–649. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining (KDD), Portland, OR, USA, 2–4 August 1996; Volume 96, pp. 226–231. [Google Scholar]
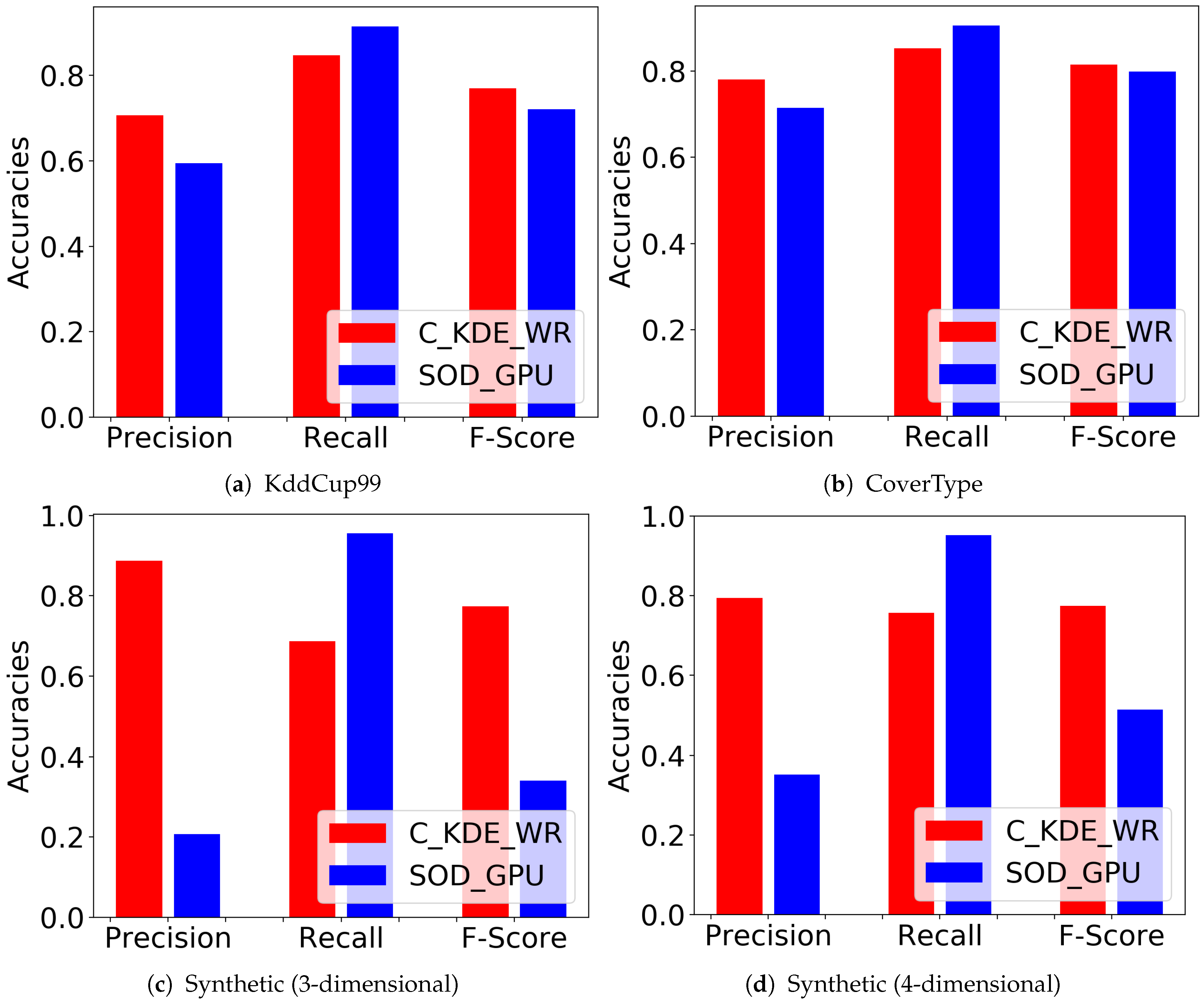


| KddCup99 Dataset | CoverType Dataset | Synthetic Dataset | ||||
|---|---|---|---|---|---|---|
| Precision | F-Score | Precision | F-Score | Precision | F-Score | |
| p-value | < | < | < | < | < | < |
| confidence interval | (0.106, 0.119) | (0.045, 0.055) | (0.064, 0.680) | (0.014, 0.018) | (0.264, 0.291) | (0.018, 0.056) |
| variance | ||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, K.; Shi, W.; Santoro, N. Designing a Streaming Algorithm for Outlier Detection in Data Mining—An Incrementa Approach. Sensors 2020, 20, 1261. https://doi.org/10.3390/s20051261
Yu K, Shi W, Santoro N. Designing a Streaming Algorithm for Outlier Detection in Data Mining—An Incrementa Approach. Sensors. 2020; 20(5):1261. https://doi.org/10.3390/s20051261
Chicago/Turabian StyleYu, Kangqing, Wei Shi, and Nicola Santoro. 2020. "Designing a Streaming Algorithm for Outlier Detection in Data Mining—An Incrementa Approach" Sensors 20, no. 5: 1261. https://doi.org/10.3390/s20051261
APA StyleYu, K., Shi, W., & Santoro, N. (2020). Designing a Streaming Algorithm for Outlier Detection in Data Mining—An Incrementa Approach. Sensors, 20(5), 1261. https://doi.org/10.3390/s20051261





