Automatic, Qualitative Scoring of the Interlocking Pentagon Drawing Test (PDT) Based on U-Net and Mobile Sensor Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Subjects
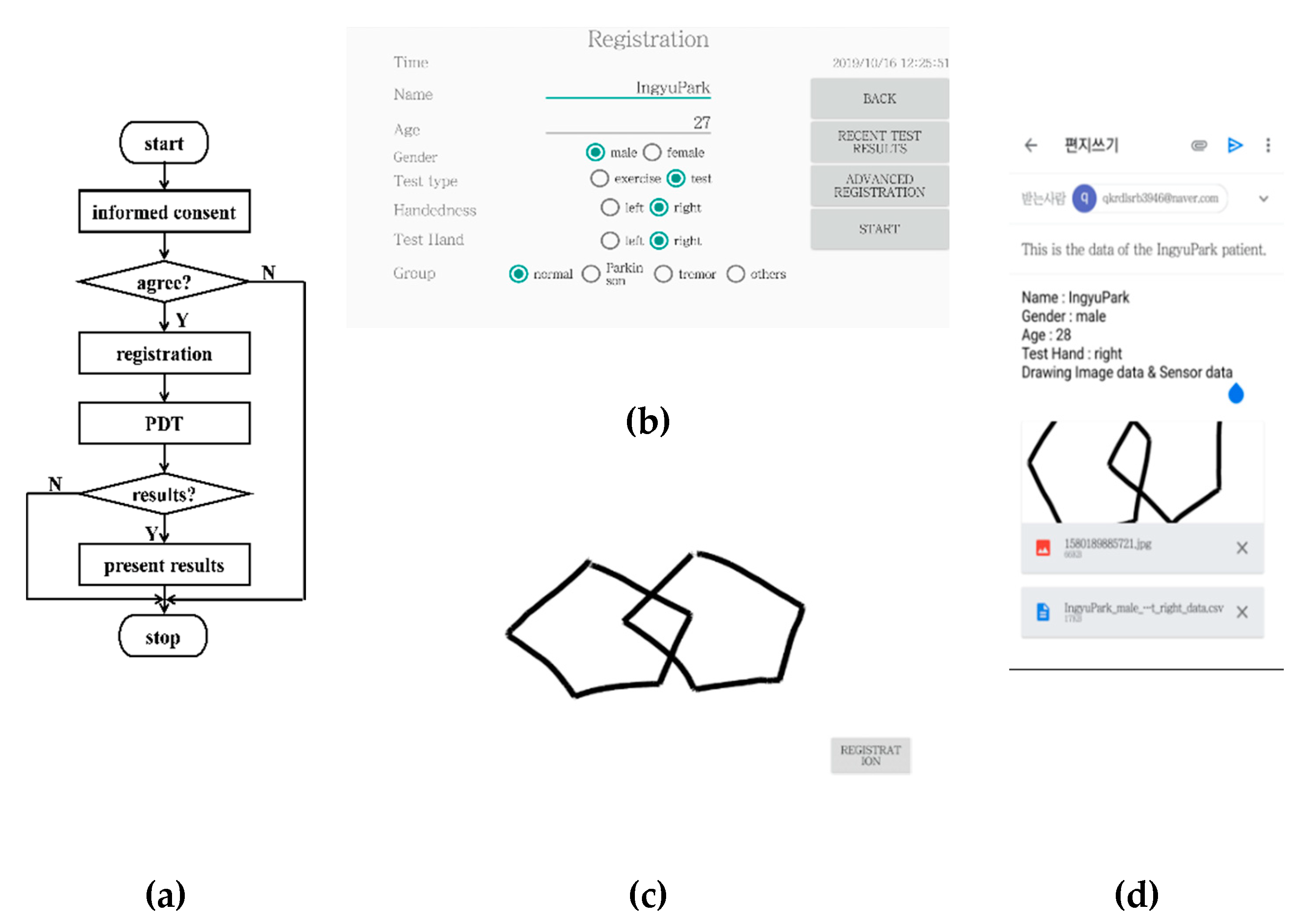
2.2. Implementation of the Mobile Pentagon Drawing Test, mPDT
2.3. Pre-Trained Models, Deep5 and DeepLock based on the U-Net
2.4. Scoring Method of mPDT
2.4.1. Sensor Data Manipulation and Shape Segmentation Using Deep5 and Deeplock
2.4.2. Number of Angles
2.4.3. Distance/Intersection between Two Figures
2.4.4. Existence of Closure/Opening
2.4.5. Existence of Tremors
2.4.6. Assignment of Scores
3. Results
3.1. Scoring of the Number of Angles
3.2. Scoreing of Distance/Interlocking
3.3. Scoring of Closure/Opening
3.4. Scoring of Tremors
3.5. Performance Test Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Mode of Drawing | Test Type | Scoring Method and Spec. | Reference |
|---|---|---|---|
| Clock drawing test (CDT) | paper-based | quantitative, semi-quantitative 5, 6, 10, 12, 20 points systems manually interpreting | [16] 2018 review |
| digital CDT | semi-quantitative automatic estimation of stroke features, up and down 6 points system manually interpreting based on computerized feature | [17] 2017 | |
| digital CDT | qualitative ontology-based knowledge representation CNN for object recognition automatically recognize each number by the probability score | [18] 2017 | |
| digital CDT | qualitative categorized stroke data based on feature using machine learning | [19] 2016 | |
| digital CDT | qualitative automatic estimation of stroke features, up and down, stroke velocity, stroke pressure | [20] 2019 | |
| Rey–Osterrieth complex figure (ROCF) | paper-based | quantitative location and perceptual grading of the basic geometric features | [21] 1944 |
| paper-based | qualitative points 0-24 based on the order in which the figure is produced | [23] 2017 | |
| paper-based | quantitative automated scoring of 18 segments based on a cascade of deep neural networks trained on human rater scores | [24] 2019 | |
| PDT | paper-based | qualitative 6 points system manually interpreting | [25] 1995 |
| paper-based | qualitative 10 points system manually interpreting | [26] 2011 | |
| paper-based | qualitative 6 sub scales manually interpreting based on factor analysis and 6 subscales correlated to control responses | [27] 2012 | |
| paper-based | qualitative points 0–13 based on parametric estimations for number of angles, distance/intersection, closure/opening, rotation, closing-in manually interpreting | [5] 2013 | |
| mPDT | mobile-based | qualitative points 0–11 based on stroke feature for the order and the speed and also parametric estimations for number of angles, distance/intersection, closure/opening, tremor automatic interpreting using U-net deep learning algorithm and sensor data | The presented system |
Appendix B
| Case Image | Performance Scores | Assigned Integer Scores | Total Score | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NA1 | D/I2 | C/O3 | Tr4 | NA1 | D/I2 | C/O3 | Tr4 | ||
 | 10 | CI5 | NO10 | NT13 | 4 | 4 | 2 | 1 | 11 |
 | 10 | CI5 | O111 | NT13 | 4 | 4 | 1 | 1 | 10 |
 | 10 | WI6 | NO10 | NT13 | 4 | 3 | 2 | 1 | 10 |
 | 10 | CI5 | O212 | NT13 | 4 | 4 | 0 | 1 | 9 |
 | 10 | WI6 | O111 | NT13 | 4 | 3 | 1 | 1 | 9 |
 | 10 | NC08 | NO10 | NT13 | 4 | 1 | 2 | 1 | 8 |
 | 10 | C7 | O111 | NT13 | 4 | 2 | 1 | 1 | 8 |
 | 9 | CI5 | NO10 | NT13 | 3 | 4 | 2 | 1 | 10 |
 | 9 | CI5 | O111 | NT13 | 3 | 4 | 1 | 1 | 9 |
 | 9 | WI6 | NO10 | NT13 | 3 | 3 | 2 | 1 | 9 |
 | 9 | C7 | NO10 | NT13 | 3 | 2 | 2 | 1 | 8 |
 | 9 | WI6 | O111 | NT13 | 3 | 3 | 1 | 1 | 8 |
 | 9 | WI6 | O212 | NT13 | 3 | 3 | 0 | 1 | 7 |
 | 9 | C7 | O111 | NT13 | 3 | 2 | 1 | 1 | 7 |
 | 11 | NC08 | O212 | NT13 | 3 | 1 | 0 | 1 | 5 |
 | 8 | CI5 | NO10 | NT13 | 2 | 4 | 2 | 1 | 9 |
 | 8 | CI5 | NO10 | NT13 | 2 | 4 | 2 | 1 | 9 |
 | 8 | WI6 | NO10 | NT13 | 2 | 3 | 2 | 1 | 8 |
 | 8 | WI6 | NO10 | NT13 | 2 | 3 | 2 | 1 | 8 |
 | 8 | WI6 | O111 | NT13 | 2 | 3 | 1 | 1 | 7 |
 | 8 | C7 | NO10 | NT13 | 2 | 2 | 2 | 1 | 7 |
 | 8 | NC08 | NO10 | NT13 | 2 | 1 | 2 | 1 | 6 |
 | 8 | NC08 | O111 | NT13 | 2 | 1 | 1 | 1 | 5 |
 | 8 | NC19 | NO10 | NT13 | 2 | 0 | 2 | 1 | 5 |
 | 8 | NC08 | O212 | NT13 | 2 | 1 | 0 | 1 | 4 |
 | 7 | CI5 | NO10 | NT13 | 1 | 4 | 2 | 1 | 8 |
 | 7 | NC08 | NO10 | NT13 | 1 | 1 | 2 | 1 | 5 |
 | 7 | NC19 | NO10 | NT13 | 1 | 0 | 2 | 1 | 4 |
 | 7 | NC19 | O111 | NT13 | 1 | 0 | 1 | 1 | 3 |
 | 6 | NC19 | O111 | NT13 | 1 | 0 | 1 | 1 | 3 |
 | >13 | WI6 | NO10 | NT13 | 0 | 3 | 2 | 1 | 6 |
 | >13 | CI5 | O212 | NT13 | 0 | 4 | 0 | 1 | 5 |
 | >13 | NC08 | O111 | NT13 | 0 | 1 | 1 | 0 | 2 |
 | >13 | C7 | O212 | T14 | 0 | 2 | 0 | 0 | 2 |
 | 4 | NC19 | O212 | NT13 | 0 | 0 | 0 | 1 | 1 |
 | 4 | NC19 | O212 | T14 | 0 | 0 | 0 | 0 | 0 |
Appendix C


| Case of Image of the Left-Handed Subject | Performance Scores | Assigned Integer Scores | Total Score | ||||||
|---|---|---|---|---|---|---|---|---|---|
| NA1 | D/I2 | C/O3 | Tr4 | NA1 | D/I2 | C/O3 | Tr4 | ||
 | 10 | CI5 | NO6 | NT7 | 4 | 4 | 2 | 1 | 11 |
 | 10 | CI5 | NO6 | NT7 | 4 | 4 | 2 | 1 | 11 |
References
- Folstein, M.F.; Folstein, S.E.; McHugh, P.R. Mini-mental state: A practical method for grading the cognitive state of patients for the clinician. J. Psychiatr. Res. 1975, 12, 189–198. [Google Scholar] [CrossRef]
- Biundo, R.; Weis, L.; Bostantjopoulou, S.; Stefanova, E.; Falup-Pecurariu, C.; Kramberger, M.G.; Geurtsen, G.J.; Antonini, A.; Weintraub, D.; Aarsland, D. MMSE and MoCA in Parkinson’s disease and dementia with Lewy bodies: A multicenter 1-year follow-up study. J. Neural Transm. 2016, 123, 431–438. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Błaszczyk, J.W. Parkinson’s Disease and Neurodegeneration: GABA-Collapse Hypothesis. Front. Neurosci. 2016, 10. [Google Scholar] [CrossRef] [Green Version]
- Hely, M.A.; Reid, W.G.; Adena, M.A.; Halliday, G.M.; Morris, J.G. The Sydney Multicenter Study of Parkinson’s Disease: The Inevitability of Dementia at 20 years. Mov. Disord. 2008, 23, 837–844. [Google Scholar] [CrossRef] [PubMed]
- Caffarraa, P.; Gardinia, S.; Diecib, F.; Copellib, S.; Maseta, L.; Concaria, L.; Farinac, E.; Grossid, E. The qualitative scoring MMSE pentagon test (QSPT): A new method for differentiating dementia with Lewy Body from Alzheimer’s Disease. Behav. Neurol. 2013, 27, 213–220. [Google Scholar] [CrossRef]
- Cecato, J.F. Pentagon Drawing Test: Some data from Alzheimer’s disease, Paraphrenia and Obsessive compulsive disorder in elderly patients. Perspect. Psicol. 2016, 13, 21–26. [Google Scholar]
- Ala, T.A.; Hughes, L.F.; Kyrouac, G.A.; Ghobrial, M.W.; Elble, R.J. Pentagon copying is more impaired in dementia with Lewy bodies than in Alzheimer’s disease. J. Neurol. Neurosurg. Psychiatry 2001, 70, 483–488. [Google Scholar] [CrossRef] [Green Version]
- Teng, E.L.; Chui, H.C. The modified Mini-Mental State (3-MS) Examination. J. Clin. Psychiatry 1987, 48, 314–318. [Google Scholar]
- Martinelli, J.E.; Cecato, J.F.; Msrtinelli, M.O.; Melo, B.A.R.; Aprahamian, I. Performance of the Pentagon Drawing test for the screening of older adults with Alzheimer’s dementia. Dement. Neuropsychol. 2018, 12, 54–60. [Google Scholar] [CrossRef]
- Lam, M.W.Y.; Liu, X.; Meng, H.M.L.; Tsoi, K.K.F. Drawing-Based Automatic Dementia Screening Using Gaussian Process Markov Chains. In Proceedings of the 51st Hawaii International Conference on System Sciences, Hilton Waikoloa Village, HI, USA, 1 January 2018. [Google Scholar]
- Mervis, C.B.; Robinson, B.F.; Pani, J.R. Cognitive and behavioral genetics ’99 visuospatial construction. Am. J. Hum. Genet. 1999, 65, 1222–1229. [Google Scholar] [CrossRef] [Green Version]
- Johnson, D.K.; Storandt, M.; Morris, J.C.; Galvin, J.E. Longitudinal study of the transition from healthy aging to Alzheimer disease. Arch. Neurol. 2009, 66, 1254–1259. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aprahamian, I.; Martinelli, J.E.; Neri, A.L.; Yassuda, M.S. The clock drawing test: A review of its accuracy in screening for dementia. Dement. Neuropsychol. 2009, 3, 74–80. [Google Scholar] [CrossRef] [PubMed]
- McGee, S. Evidence-Based Physical Diagnosis, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 49–56. [Google Scholar]
- Spenciere, B.; Alves, H.; Charchat-Fichman, H. Scoring systems for the Clock Drawing Test, A historical review. Dement. Neuropsychol 2017, 11, 6–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palsetia, D.; Prasad Rao, G.; Tiwari, S.C.; Lodha, P.; De Sousa, A. The Clock Drawing Test versus Mini-mental Status Examination as a Screening Tool for Dementia: A Clinical Comparison. Indian J. Psychol. Med. 2018, 40, 1–10. [Google Scholar] [PubMed]
- Müller, S.; Preische, O.; Heymann, P.; Elbing, U.; Laske, C. Increased Diagnostic Accuracy of Digital vs. Conventional Clock Drawing Test for Discrimination of Patients in the Early Course of Alzheimer’s Disease from Cognitively Healthy Individuals. Front. Aging Neurosci. 2017, 9. [Google Scholar] [CrossRef] [Green Version]
- Harbi, Z.; Hicks, Y.; Setchi, R. Clock Drawing Test Interpretation System. In Proceedings of the International Conference on Knowledge Based and Intelligent Information and Engineering Systems, KES2017, Marseille, France, September 2017. [Google Scholar]
- Souillard-Mandar, W.; Davis, R.; Rudin, C.; Au, R.; Libon, D.J.; Swenson, R.; Price, C.C.; Lamar, M.; Penney, D.L. Learning Classification Models of Cognitive Conditions from Subtle Behaviors in the Digital Clock Drawing Test. Mach. Learn. 2016, 102, 393–441. [Google Scholar] [CrossRef]
- Müller, S.; Herde, L.; Preische, O.; Zeller, A.; Heymann, P.; Robens, S.; Elbing, U.; Laske, C. Diagnostic value of digital clock drawing test in comparison with CERAD neuropsychological battery total score for discrimination of patients in the early course of Alzheimer’s disease from healthy Individuals. Sci. Rep. 2019, 9, 3543. [Google Scholar] [CrossRef] [Green Version]
- Osterrieth, P.A. Filetest de copie d’une figure complex: Contribution a l’etude de la perception et de la memoire The test of copying a complex figure: A contribution to the study of perception and memory. Arch. Psychol. 1944, 30, 286–356. [Google Scholar]
- Canham, R.O.; Smith, S.L.; Tyrrell, A.M. Automated Scoring of a Neuropsychological Test: The Rey Osterrieth Complex Figure. In Proceedings of the 26th Euromicro Conference. EUROMICRO 2000. Informatics: Inventing the Future, Maastricht, The Netherlands, 5–7 September 2000; Volume 2, pp. 406–413. [Google Scholar]
- Sargenius, H.L.; Bylsma, F.W.; Lydersen, S.; Hestad, K. Visual-Constructional Ability in Individuals with Severe Obesity: Rey Complex Figure Test Accuracy and the Q-Score. Front. Psychol. 2017, 8, 1629. [Google Scholar] [CrossRef]
- Vogt, J.; Kloosterman, H.; Vermeent, S.; Van Elswijk, G.; Dotsch, R.; Schmand, B. Automated scoring of the Rey-Osterrieth Complex Figure Test using a deep-learning algorithm. Arch. Clin. Neuropsychol. 2019, 34, 836. [Google Scholar] [CrossRef]
- Bourke, J.; Castleden, C.M.; Stephen, R.; Dennis, M. A comparison of clock and pentagon drawing in Alzheimer’s disease. Int. J. Geriatr. Psychiatry 1995, 10, 703–705. [Google Scholar] [CrossRef]
- Nagaratnam, N.; Nagaratnam, K.; O’Mara, D. Intersecting pentagon copying and clock drawing test in mild and moderate Alzheimer’s disease. J. Clin. Gerontol. Geriatr. 2014, 5, 47–52. [Google Scholar] [CrossRef] [Green Version]
- Fountoulakis, K.N.; Siamouli, M.; Panagiotidis, P.T.; Magiria, S.; Kantartzis, S.; Terzoglou, V.A.; Oral, T. The standardised copy of pentagons test. Ann. Gen. Psychiatry 2011. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, E.-S.; Hong, Y.J.; Yoon, B.; Lim, S.-C.; Shim, Y.S.; Ahn, K.J.; Cho, A.-H.; Yang, D.-W. Anatomical Correlates of Interlocking Pentagon Drawing. Dement. Neurocogn. Disord. 2012, 11, 141–145. [Google Scholar] [CrossRef] [Green Version]
- Cormack, F.; Aarsland, D.; Ballard, C.; Tovée, M.J. Pentagon drawing and neuropsychological performance in Dementia with Lewy Bodies, Alzheimer’s disease, Parkinson’s disease and Parkinson’s disease with dementia. Int. J. Geriatr. Psychiatry 2004, 19, 371–377. [Google Scholar] [CrossRef]
- Beretta, L.; Caminiti, S.P.; Santangelo, R.; Magnani, G.; Ferrari-Pellegrini, F.; Caffarra, P.; Perani, D. Two distinct pathological substrates associated with MMSE-pentagons item deficit in DLB and AD. Neuropsychologia 2019, 133, 104–174. [Google Scholar] [CrossRef]
- Vergouw, L.J.M.; Salomé, M.; Kerklaan, A.G.; Kies, C.; Roks, G.; van den Berg, E.; de Jong, F.J. The Pentagon Copying Test and the Clock Drawing Test as Prognostic Markers in Dementia with Lewy Bodies. Dement. Geriatr. Cogn. Disord. 2018, 45, 308–317. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015; Navab, N., Hornegger, J., Wells, W., Frangi, A., Eds.; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Matt, E.; Foki, T.; Fischmeister, F.; Pirker, W.; Haubenberger, D.; Rath, J.; Lehrner, J.; Auff, E.; Beisteiner, R. Early dysfunctions of fronto-parietal praxis networks in Parkinson’s disease. Brain Imaging Behav. 2017, 11, 512–525. [Google Scholar] [CrossRef] [Green Version]
- Potgieser, A.R.E.; van der Hoorn, A.; de Jong, B.M. Cerebral Activations Related to Writing and Drawing with Each Hand. PLoS ONE 2015. [Google Scholar] [CrossRef]
- Segal, E.; Petrides, M. The anterior superior parietal lobule and its interactions with language and motor areas during writing. Eur. J. Neurosci. 2012, 35, 309–322. [Google Scholar] [CrossRef]
- Makuuchi, M.; Kaminaga, T.; Sugishita, M. Both parietal lobes are involved in drawing: A functional MRI study and implications for constructional apraxia. Cogn. Brain Res. 2003, 16, 338–347. [Google Scholar] [CrossRef]
- De Lucia, N.; Grossi, D.; Trojano, L. The genesis of closing-in in alzheimer disease and vascular dementia: A comparative clinical and experimental study. Neurophysiology 2014, 28, 312–318. [Google Scholar] [CrossRef] [PubMed]
- Ryu, H.-S. New Classification of Tremors: 2018 International Parkinson and Movement Disorder Society. J. Korean Neurol. Assoc. 2019, 37, 251–261. [Google Scholar] [CrossRef] [Green Version]
- Kulisevsky, J.; Pagonabarrage, J. Cognitive Impairment in Parkinson’s Disease: Tools for Diagnosis and Assessment. Mov. Disord. 2009, 24, 1103–1110. [Google Scholar] [CrossRef] [PubMed]






| Training Set | Test Set | ||
|---|---|---|---|
| Volunteers (n = 199) | Volunteers (n = 129) | PD Patients (n = 101) | |
| Age (mean ± standard deviation) | 22.11 ± 1.44 | 26.87 ± 1.84 | 75.86 ± 8.13 |
| Gender (male/female) | 107/92 | 68/61 | 47/54 |
| Binary PDT score (Pass/Nonpass ) | 199/0 | 48/81 | 32/69 |
| Parameters | Performance Scores | Assigned Integer Scores |
|---|---|---|
| Number of Angles | 10 | 4 |
| 9 or 11 | 3 | |
| 8 or 12 | 2 | |
| 7–5 | 1 | |
| < 5 or > 13 | 0 | |
| Distance/Intersection | Correct intersection | 4 |
| Wrong intersection | 3 | |
| Contact without intersection | 2 | |
| No contact, distance < 1 cm | 1 | |
| No contact, distance > 1 cm | 0 | |
| Closure/Opening | Closure both figures | 2 |
| Closure only one figure | 1 | |
| Opening both figures | 0 | |
| Tremor | No tremor | 1 |
| Tremor | 0 | |
| Total | 0–11 |
| Parameters | Assigned Integer Scores | Conditions (Scoring Method) |
|---|---|---|
| Number of angles | 4 | and |
| 3 | or , = 9 or 11 | |
| 2 | or , = 8 or 12 | |
| 1 | or , 5 ≤ ≤ 7 | |
| 0 | or , < 5 or >13 | |
| Distance/intersection | 4 | , , |
| 3 | , , | |
| 2 | , | |
| 1 | , | |
| 0 | , | |
| Closure/opening | 2 | , |
| 1 | , | |
| 0 | , | |
| Tremor | 1 | |
| 0 |
| Scores | Number of Angles | Distance/Intersection | Closure/Opening | Tremor |
|---|---|---|---|---|
| 4 | 80 | 87 | - | - |
| 3 | 30 | 38 | - | - |
| 2 | 33 | 34 | 130 | - |
| 1 | 32 | 38 | 61 | 214 |
| 0 | 55 | 33 | 39 | 16 |
| total | 230 | 230 | 230 | 230 |
| Number of Angles | Distance/Intersection | Closure/Opening | Tremor | |
|---|---|---|---|---|
| TP | 79 | 81 | 126 | 214 |
| FP | 11 | 3 | 9 | 0 |
| FN | 2 | 6 | 8 | 0 |
| TN | 138 | 140 | 87 | 16 |
| Sensitivity | 97.53 | 93.10 | 94.03 | 100.00 |
| Specificity | 92.62 | 97.90 | 90.63 | 100.00 |
| Accuracy | 94.35 | 96.09 | 92.61 | 100.00 |
| Precision | 87.78 | 96.43 | 93.33 | 100.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, I.; Kim, Y.J.; Kim, Y.J.; Lee, U. Automatic, Qualitative Scoring of the Interlocking Pentagon Drawing Test (PDT) Based on U-Net and Mobile Sensor Data. Sensors 2020, 20, 1283. https://doi.org/10.3390/s20051283
Park I, Kim YJ, Kim YJ, Lee U. Automatic, Qualitative Scoring of the Interlocking Pentagon Drawing Test (PDT) Based on U-Net and Mobile Sensor Data. Sensors. 2020; 20(5):1283. https://doi.org/10.3390/s20051283
Chicago/Turabian StylePark, Ingyu, Yun Joong Kim, Yeo Jin Kim, and Unjoo Lee. 2020. "Automatic, Qualitative Scoring of the Interlocking Pentagon Drawing Test (PDT) Based on U-Net and Mobile Sensor Data" Sensors 20, no. 5: 1283. https://doi.org/10.3390/s20051283
APA StylePark, I., Kim, Y. J., Kim, Y. J., & Lee, U. (2020). Automatic, Qualitative Scoring of the Interlocking Pentagon Drawing Test (PDT) Based on U-Net and Mobile Sensor Data. Sensors, 20(5), 1283. https://doi.org/10.3390/s20051283




