ANN-Based Airflow Control for an Oscillating Water Column Using Surface Elevation Measurements
Abstract
:1. Introduction
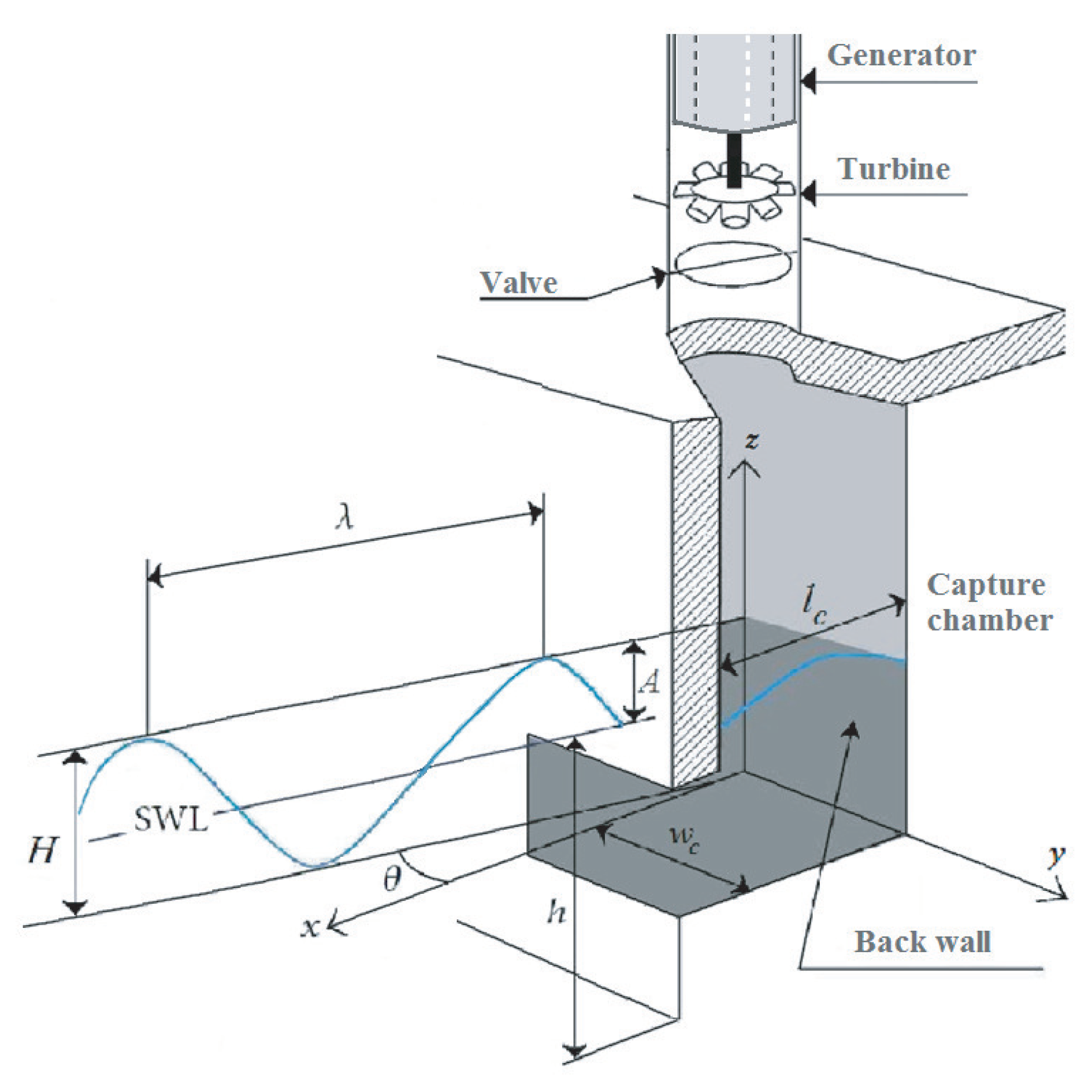
2. Model Statement
2.1. Wave Surface Dynamics
2.2. Capture Chamber Model
2.3. Wells Turbine Model
2.4. Doubly Fed Induction Generator Model
3. Problem Statement
4. Control Statement
4.1. ANN-Based Airflow Control
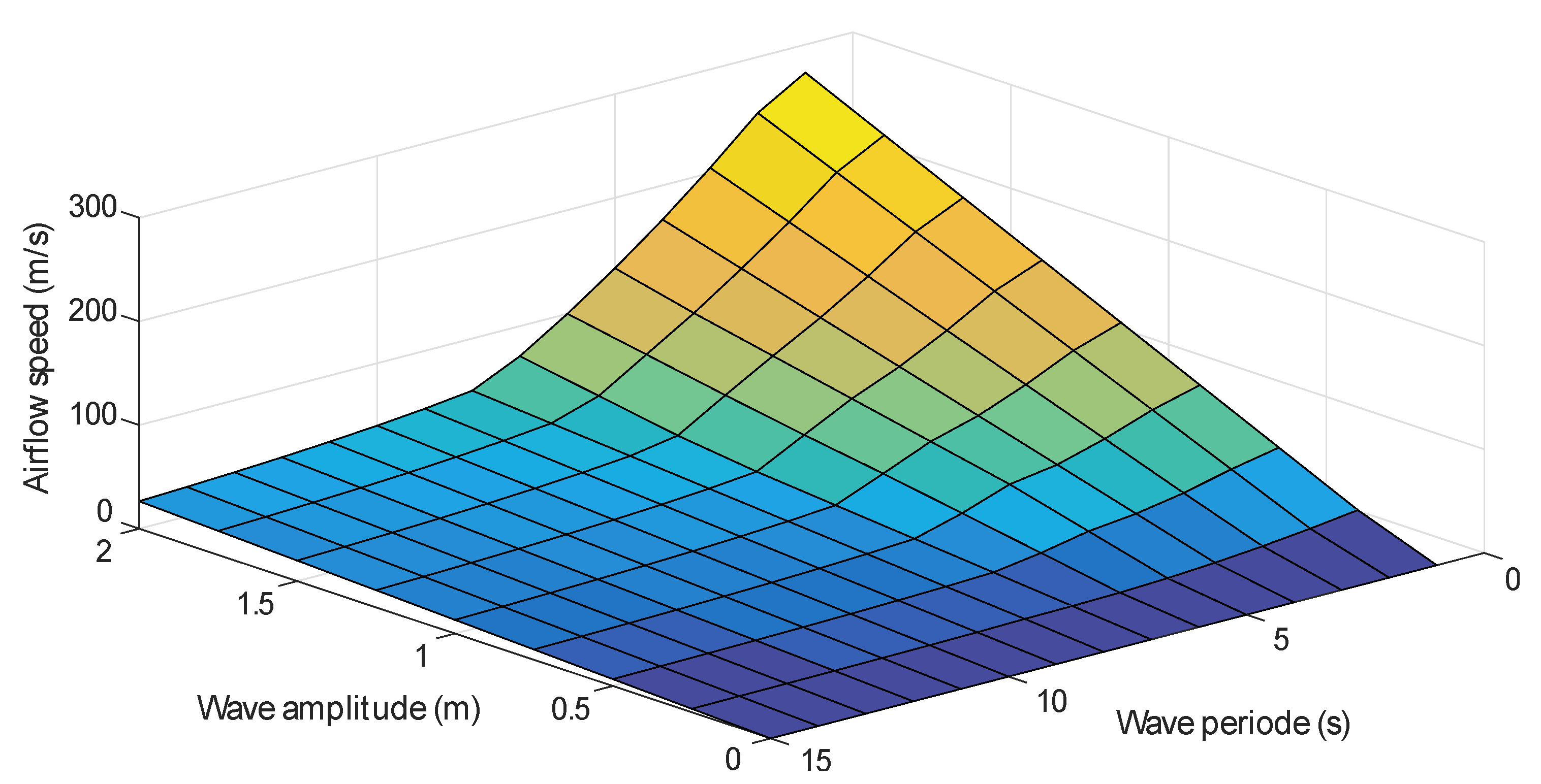
4.2. ANN Airflow Velocity Reference Generator
5. Results and Discussion
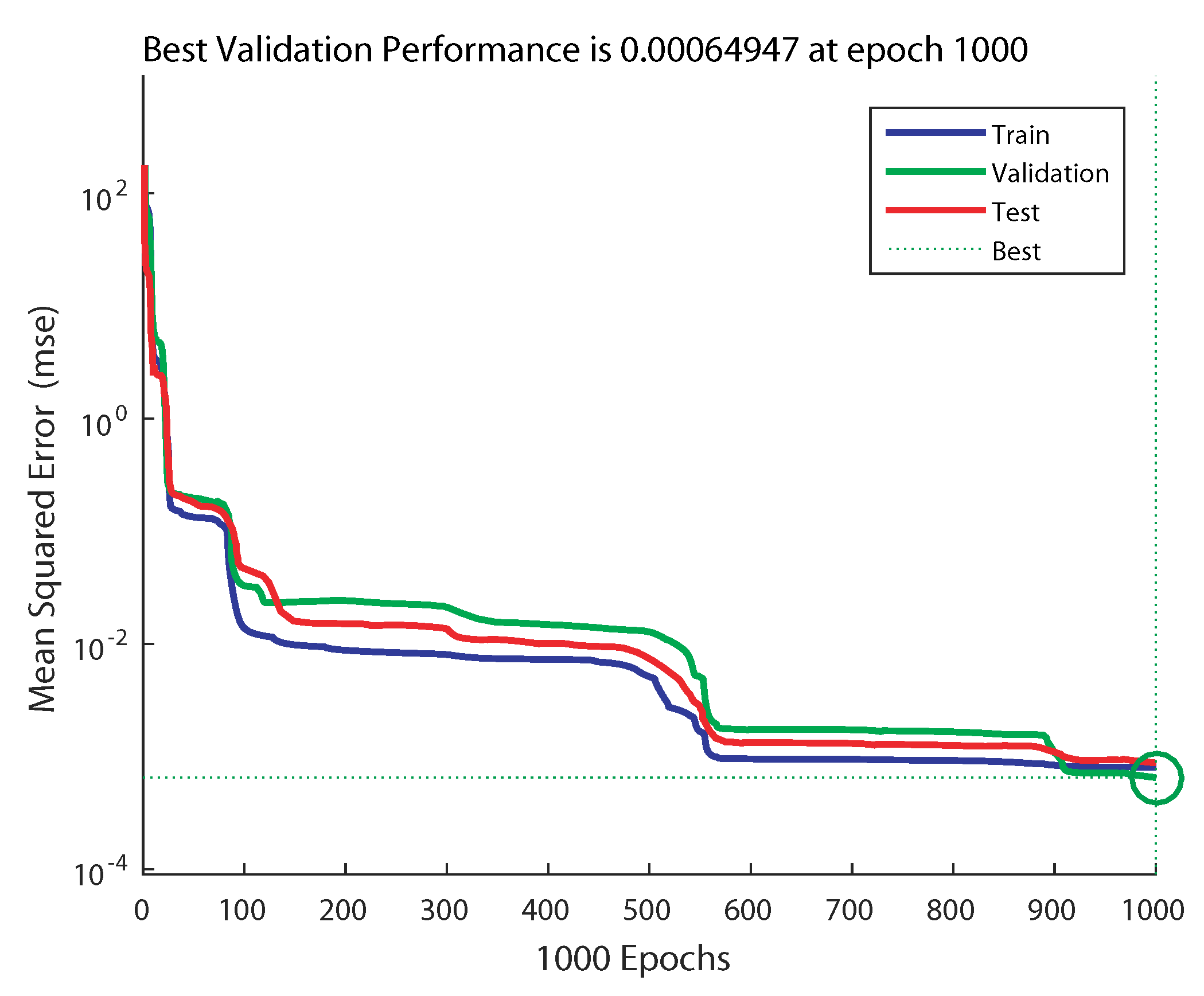
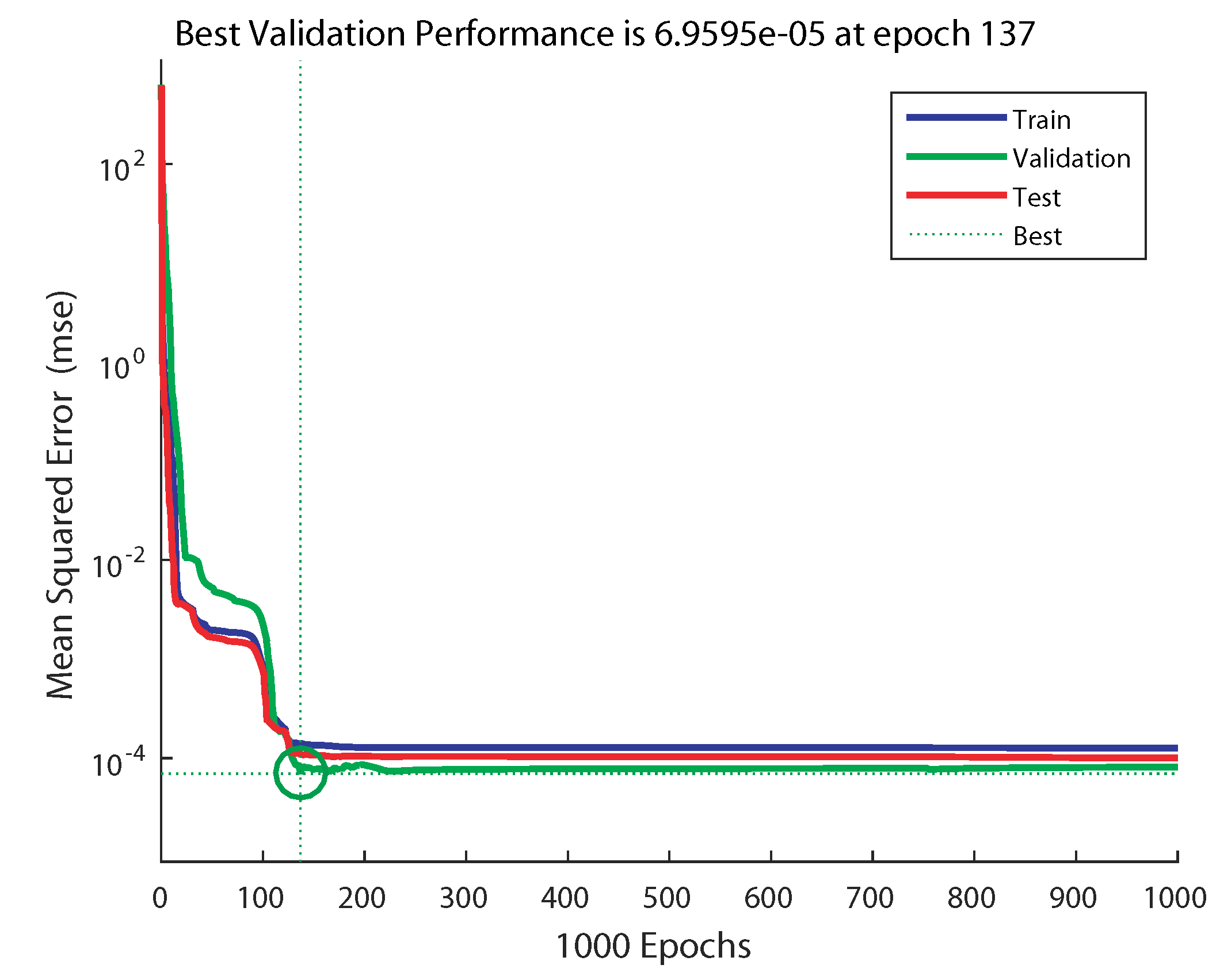
5.1. ANN Training Performance
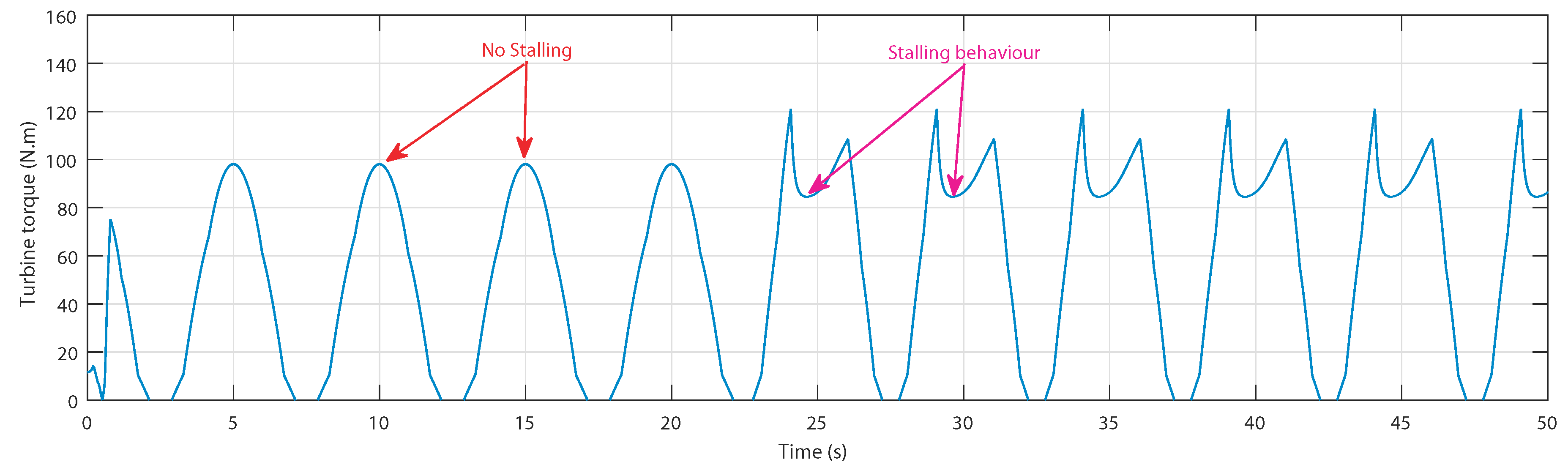
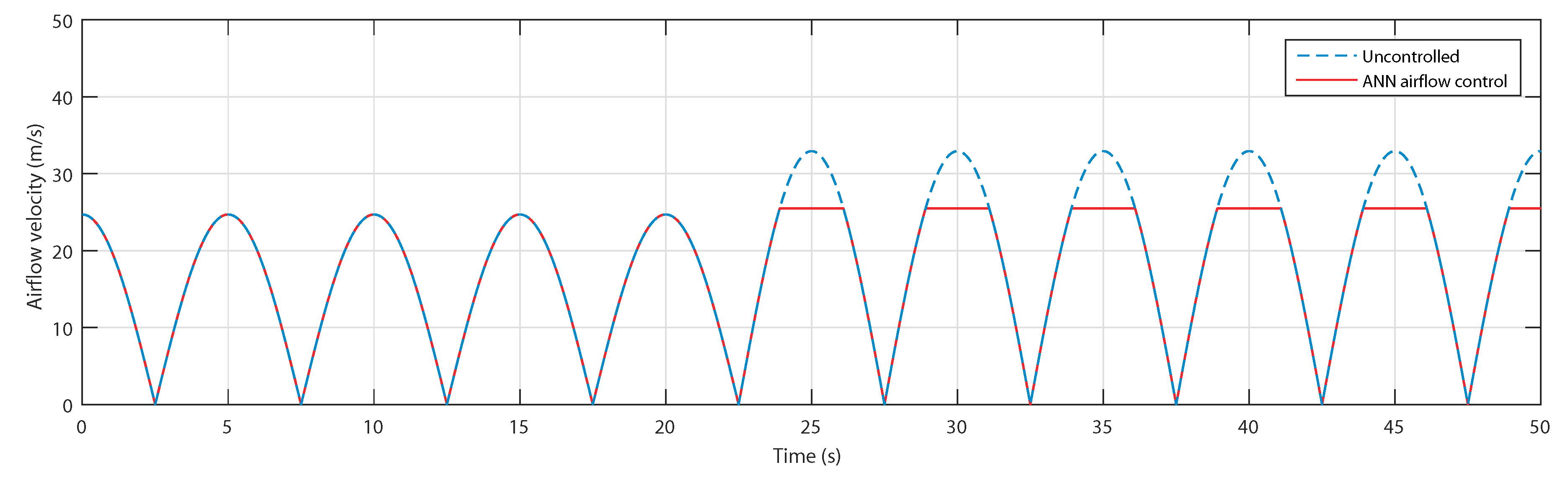
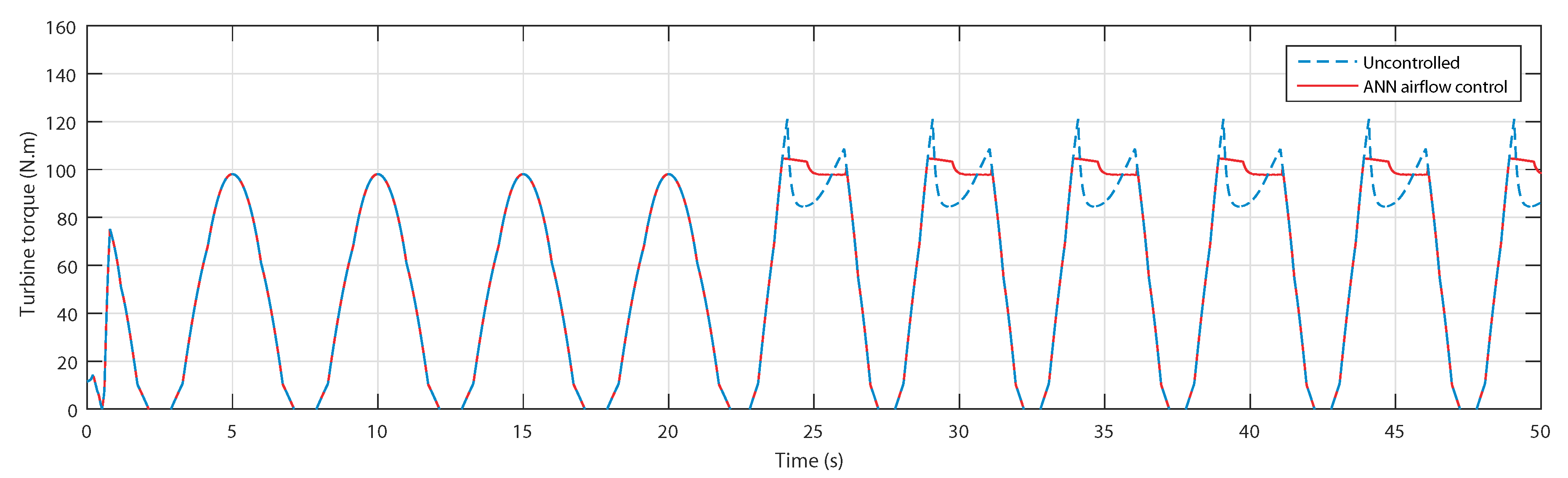
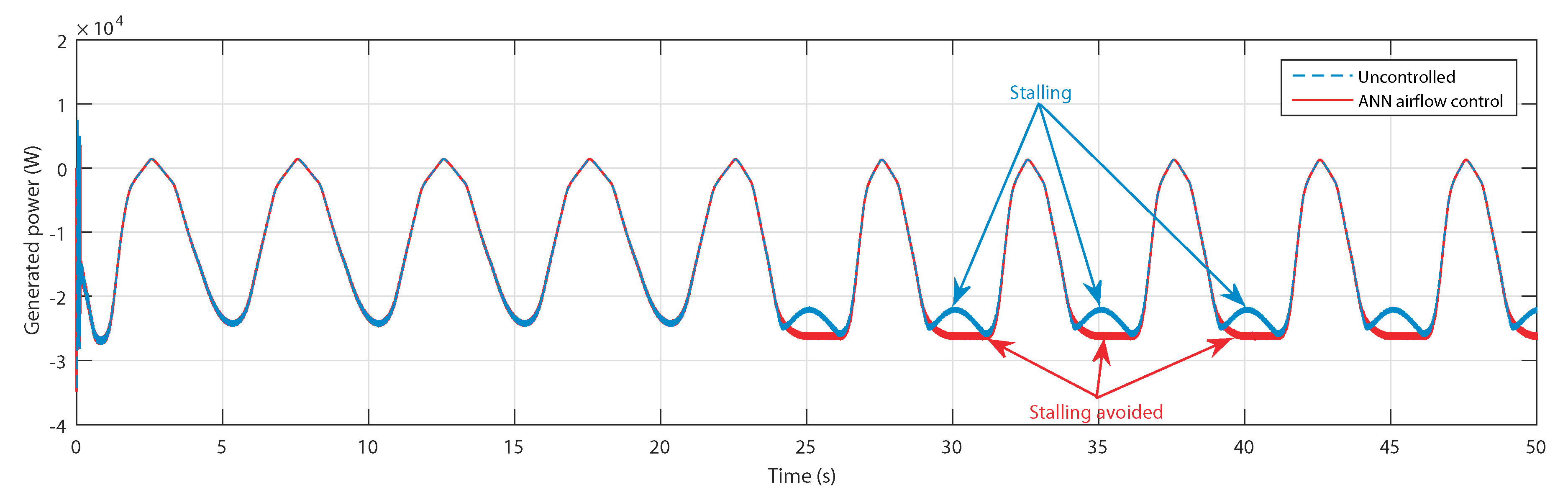
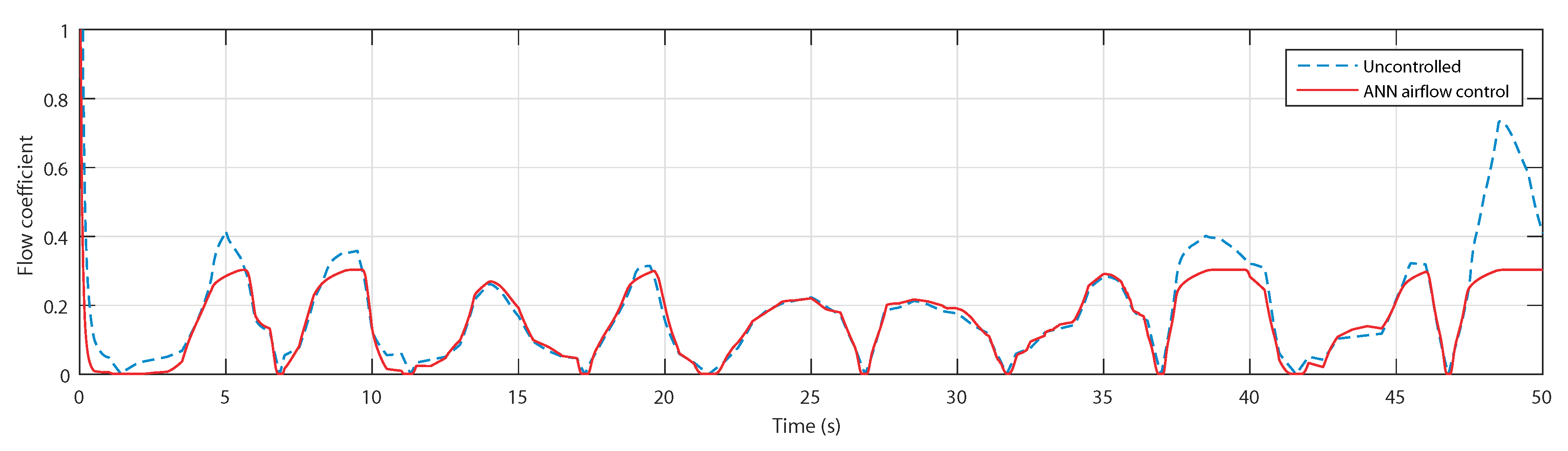
5.2. Control Assessment with Regular Waves
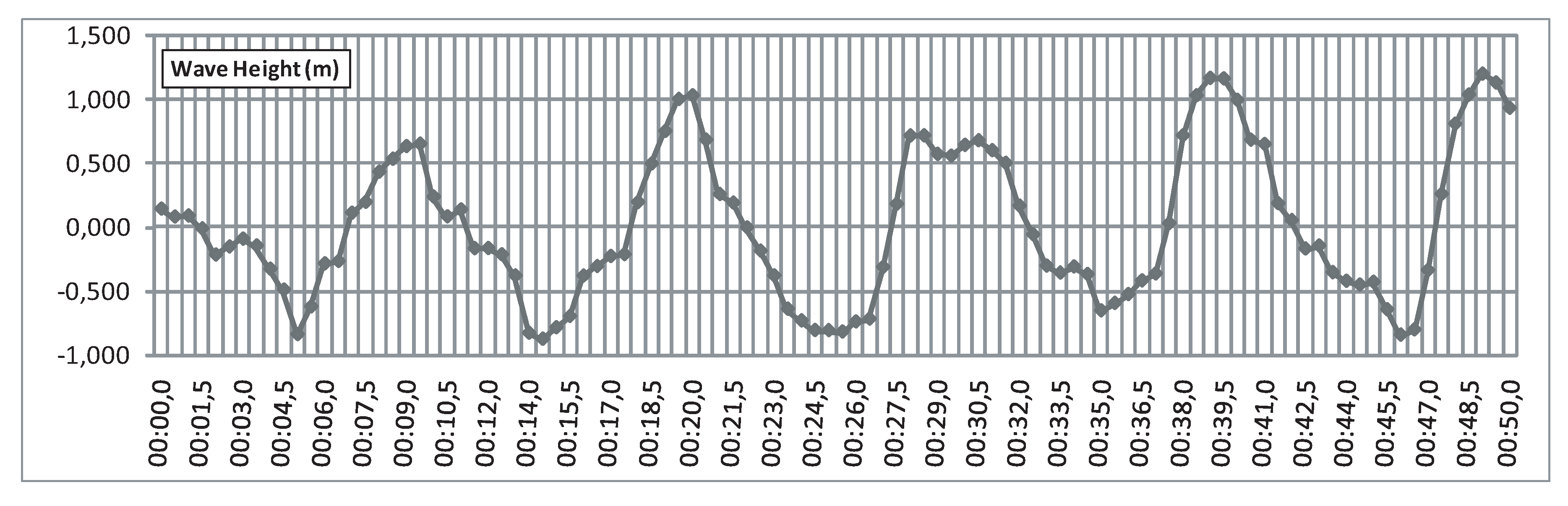
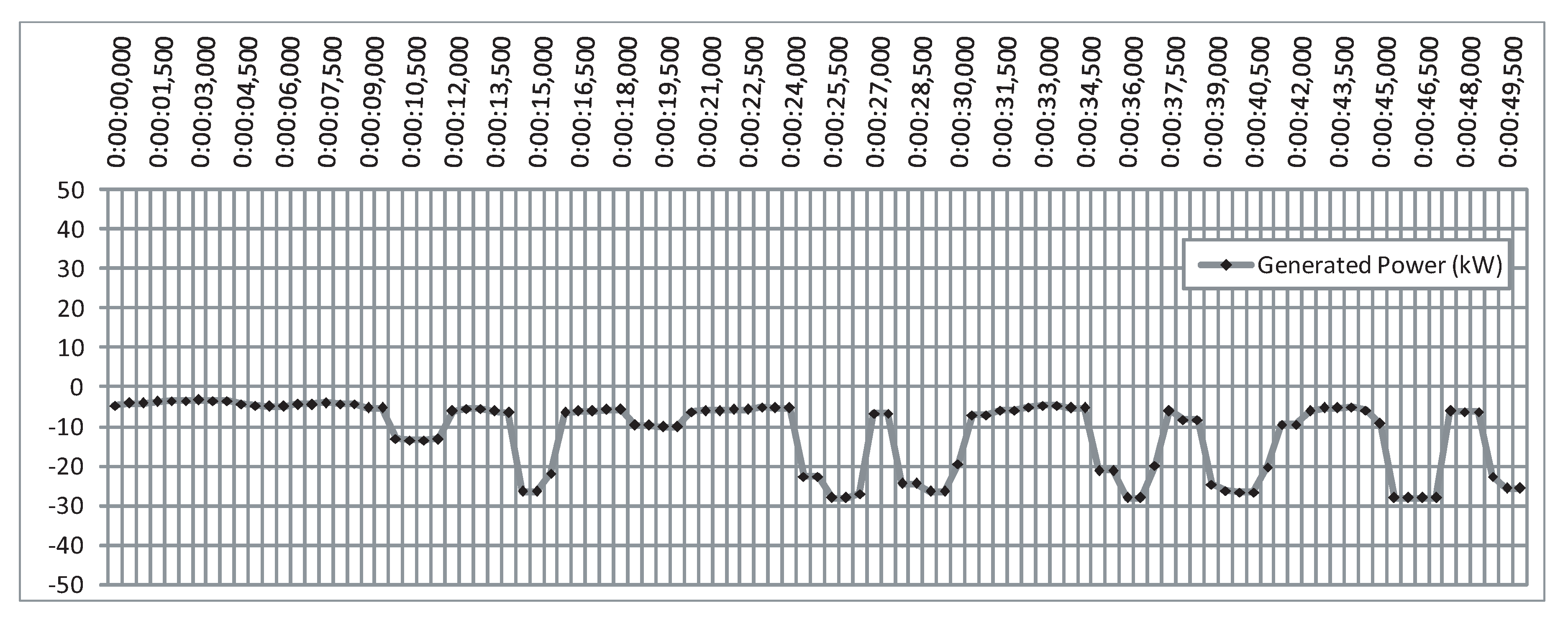
5.3. Control Assessment with Real Measured Wave Data
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Wavelength, amplitude, and height (m) | |
| Sea depth and wave surface elevation (m) | |
| Wave period (s) and wave frequency () | |
| g | Acceleration gravity () |
| Capture chamber pressure and Pressure drop () | |
| Capture chamber inner width and length (m) | |
| Capture chamber volume () and flow rate () | |
| Atmospheric density () and airflow speed () | |
| Blade chord length, blade span and turbine diameter (m) | |
| Blade number, pole number, wave number and turbine constant | |
| Electromagnetic and turbine torques () | |
| J | Turbo-generator inertia () |
| Torque, power and flow coefficients | |
| Stator and rotor resistances () | |
| Stator and rotor inductances (H) | |
| Stator and rotor currents (A) | |
| Stator and rotor flux () | |
| Stator and rotor rotational speed () | |
| Sum function, activation function, bias and output of the neuron | |
| output of neuron from previous layer and output of the neuron from current layer | |
| Weight of signal connecting neuron from previous layer to neuron of current layer |
References
- Huckerby, J.; Jeffrey, H.; Jay, B.; Executive, O. An International Vision for Ocean Energy; Ocean Energy Systems: Lisbon, Portugal, 2011. [Google Scholar]
- Brito, A.; Villate, J.L. Annual Report 2014: Implementing Agreement on Ocean Energy Systems; Ocean Energy Systems: Lisbon, Portugal, 2015. [Google Scholar]
- Lehmann, M.; Karimpour, F.; Goudey, C.A.; Jacobson, P.T.; Alam, M.R. Ocean wave energy in the United States: Current status and future perspectives. Renew. Sustain. Energy Rev. 2017, 74, 1300–1313. [Google Scholar] [CrossRef]
- Alamir, M.; Fiacchini, M.; Chabane, S.B.; Bacha, S.; Kovaltchouk, T. Active power control under Grid Code constraints for a tidal farm. In Proceedings of the 2016 Eleventh International Conference on Ecological Vehicles and Renewable Energies (EVER), New York, NY, USA, 6–8 April 2016; pp. 1–7. [Google Scholar]
- Magagna, D.; Uihlein, A. 2014 JRC Ocean Energy Status Report; European Commission: Luxembourg, 2015. [Google Scholar]
- Rusu, L.; Onea, F. Assessment of the performances of various wave energy converters along the European continental coasts. Energy 2015, 82, 889–904. [Google Scholar] [CrossRef]
- Heath, T.V. A review of oscillating water columns. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 235–245. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lagoun, M.S.; Benalia, A.; Benbouzid, M.H. Ocean wave converters: State of the art and current status. In Proceedings of the 2010 IEEE International Energy Conference, Manama, Bahrain, 18–22 December 2010; pp. 636–641. [Google Scholar]
- Yemm, R.; Pizer, D.; Retzler, C.; Henderson, R. Pelamis: Experience from concept to connection. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2012, 370, 365–380. [Google Scholar] [CrossRef] [Green Version]
- Kofoed, J.P.; Frigaard, P.; Friis-Madsen, E.; Sørensen, H.C. Prototype testing of the wave energy converter wave dragon. Renew. Energy 2006, 31, 181–189. [Google Scholar] [CrossRef] [Green Version]
- Westwood, A. SeaGen installation moves forward. Renew. Energy Focus 2008, 9, 26–27. [Google Scholar] [CrossRef]
- Calcagno, G.; Salvatore, F.; Greco, L.; Moroso, A.; Eriksson, H. Experimental and numerical investigation of an innovative technology for marine current exploitation: The Kobold turbine. In Proceedings of the Sixteenth International Offshore and Polar Engineering Conference, San Francisco, CA, USA, 28 May–2 June 2006; pp. 323–330. [Google Scholar]
- Kinsey, T.; Dumas, G.; Lalande, G.; Ruel, J.; Mehut, A.; Viarouge, P.; Lemay, J.; Jean, Y. Prototype testing of a hydrokinetic turbine based on oscillating hydrofoils. Renew. Energy 2011, 36, 1710–1718. [Google Scholar] [CrossRef]
- Stopa, J.E.; Cheung, K.F.; Chen, Y.L. Assessment of wave energy resources in Hawaii. Renew. Energy 2011, 36, 554–567. [Google Scholar] [CrossRef]
- Liberti, L.; Carillo, A.; Sannino, G. Wave energy resource assessment in the Mediterranean, the Italian perspective. Renew. Energy 2013, 50, 938–949. [Google Scholar] [CrossRef]
- Kumar, V.S.; Anoop, T.R. Wave energy resource assessment for the Indian shelf seas. Renew. Energy 2015, 76, 212–219. [Google Scholar] [CrossRef]
- López, M.; Veigas, M.; Iglesias, G. On the wave energy resource of Peru. Energy Convers. Manag. 2015, 90, 34–40. [Google Scholar] [CrossRef]
- Drew, B.; Plummer, A.R.; Sahinkaya, M.N. A review of wave energy converter technology. Proc. Inst. Mech. Eng. A J. Power Energy 2009, 223, 887–902. [Google Scholar] [CrossRef] [Green Version]
- Antonio, F.D.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar]
- Corsatea, T.D.; Magagna, D. Overview of European Innovation Activities in Marine Energy Technology; JRC Science and Policy Reports; European Commission: Brussels, Belgium, 2013. [Google Scholar]
- European Commission. Report on the Blue Growth Strategy Towards More Sustainable Growth and Jobs in the Blue Economy; European Commission: Brussels, Belgium, 2017; pp. 1–62. Available online: Https://ec.europa.eu/maritimeaffairs/policy/blue_growth_en (accessed on 28 February 2020).
- Raghunathan, S. Performance of the Wells self-rectifying turbine. Aeronaut. J. 1985, 89, 369–379. [Google Scholar]
- Raghunathan, S. The wells air turbine for wave energy conversion. Prog. Aerospace Sci. 1995, 31, 335–386. [Google Scholar] [CrossRef]
- Falcão, A.D.O.; Justino, P.A.P. OWC wave energy devices with air flow control. Ocean Eng. 1999, 26, 1275–1295. [Google Scholar] [CrossRef]
- Amundarain, M.; Alberdi, M.; Garrido, A.J.; Garrido, I. Modeling and simulation of wave energy generation plants: Output power control. IEEE Trans. Ind. Electron. 2010, 58, 105–117. [Google Scholar] [CrossRef] [Green Version]
- Mishra, S.K.; Purwar, S.; Kishor, N. Air flow control of OWC wave power plants using FOPID controller. In Proceedings of the 2015 IEEE Conference on Control Applications (CCA), Sydney, Australia, 19–22 September 2016; pp. 1516–1521. [Google Scholar]
- M’zoughi, F.; Garrido, I.; Bouallègue, S.; Ayadi, M.; Garrido, A.J. Intelligent Airflow Controls for a Stalling-Free Operation of an Oscillating Water Column-Based Wave Power Generation Plant. Electronics 2019, 8, 70. [Google Scholar] [CrossRef] [Green Version]
- Omidvar, O.; Elliott, D.L. Neural Systems for Control; Academic Press: Cambridge, MA, USA, 1997; ISBN 9780080537399. [Google Scholar]
- Yilmaz, A.S.; Ozer, Z. Pitch angle control in wind turbines above the rated wind speed by multi-layer perceptron and radial basis function neural networks. Expert Syst. Appl. 2009, 36, 9767–9775. [Google Scholar] [CrossRef]
- Alberdi, M.; Amundarain, M.; Garrido, A.; Garrido, I. Neural control for voltage dips ride-through of oscillating water column-based wave energy converter equipped with doubly-fed induction generator. Renew. Energy 2012, 48, 16–26. [Google Scholar] [CrossRef]
- Legowski, A.; Niezabitowski, M. An industrial robot singular trajectories planning based on graphs and neural networks. AIP Conf. Proc. 2016, 1738, 480057. [Google Scholar]
- Bertachi, A.; Biagi, L.; Contreras, I.; Luo, N.; Vehí, J. Prediction of Blood Glucose Levels And Nocturnal Hypoglycemia Using Physiological Models and Artificial Neural Networks. In Proceedings of the KHD@ IJCAI, Stockholm, Schweden, 13–19 July 2018; pp. 85–90. [Google Scholar]
- Farooq, Z.; Zaman, T.; Khan, M.A.; Muyeen, S.M.; Ibeas, A. Artificial Neural Network Based Adaptive Control of Single Phase Dual Active Bridge With Finite Time Disturbance Compensation. IEEE Access 2019, 7, 112229–112239. [Google Scholar] [CrossRef]
- Krzyszczak, J.; Baranowski, P.; Zubik, M.; Hoffmann, H. Temporal scale influence on multifractal properties of agro-meteorological time series. Agric. For. Meteorol. 2017, 239, 223–235. [Google Scholar] [CrossRef]
- Castañeda-Miranda, A.; Icaza-Herrera, M.D.; Castaño, V.M. Meteorological Temperature and Humidity Prediction from Fourier-Statistical Analysis of Hourly Data. Adv. Meteorol. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Yang, Z.C. Hourly ambient air humidity fluctuation evaluation and forecasting based on the least-squares Fourier-model. Measurement 2019, 133, 112–123. [Google Scholar] [CrossRef]
- Stoyanov, D.B.; Nixon, J.D. Alternative operational strategies for wind turbines in cold climates. Renew. Energy 2020, 145, 2694–2706. [Google Scholar] [CrossRef]
- Castañeda-Miranda, A.; Castaño, V.M. Smart frost control in greenhouses by neural networks models. Comput. Electron. Agric. 2017, 137, 102–114. [Google Scholar] [CrossRef]
- Li, C.; Zhou, D.; Wang, H.; Lu, Y.; Li, D. Techno-economic performance study of stand-alone wind/diesel/battery hybrid system with different battery technologies in the cold region of China. Energy 2020, 192, 116702. [Google Scholar] [CrossRef]
- Konispoliatis, D.N.; Mavrakos, S.A. Natural frequencies of vertical cylindrical oscillating water column devices. Appl. Ocean Res. 2019, 91, 101894. [Google Scholar] [CrossRef]
- Zheng, S.; Zhu, G.; Simmonds, D.; Greaves, D.; Iglesias, G. Wave power extraction from a tubular structure integrated oscillating water column. Renew. Energy 2020, 150, 342–355. [Google Scholar] [CrossRef]
- Singh, U.; Abdussamie, N.; Hore, J. Hydrodynamic performance of a floating offshore OWC wave energy converter: An experimental study. Renew. Sustain. Energy Rev. 2020, 117, 109501. [Google Scholar] [CrossRef]
- Sobey, R.; Goodwin, P.; Thieke, R.; Westberg, R.J., Jr. Application of Stokes, Cnoidal, and Fourier wave theories. J. Waterway Port Coast. Ocean Eng. 1987, 113, 565–587. [Google Scholar] [CrossRef]
- Le Roux, J.P. An extension of the Airy theory for linear waves into shallow water. Coast. Eng. 2008, 55, 295–301. [Google Scholar] [CrossRef]
- Garrido, A.J.; Otaola, E.; Garrido, I.; Lekube, J.; Maseda, F.J.; Liria, P.; Mader, J. Mathematical Modeling of Oscillating Water Columns Wave-Structure Interaction in Ocean Energy Plants. Math. Prob. Eng. 2015, 2015, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Sarmento, A.J.N.A.; de Falcão, A.F.O. Wave generation by an oscillating surface-pressure and its application in wave-energy extraction. J. Fluid Mech. 1985, 150, 467–485. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Rodrigues, R.J.A. Stochastic modelling of OWC wave power plant performance. Appl. Ocean Res. 2002, 24, 59–71. [Google Scholar] [CrossRef]
- M’zoughi, F.; Bouallègue, S.; Garrido, A.J.; Garrido, I.; Ayadi, M. Stalling-free Control Strategies for Oscillating-Water-Column-based Wave Power Generation Plants. IEEE Trans. Energy Convers. 2018, 33, 209–222. [Google Scholar] [CrossRef]
- M’zoughi, F.; Bouallègue, S.; Garrido, A.J.; Garrido, I.; Ayadi, M. Water Cycle Algorithm-based Airflow Control for an Oscillating Water Column-based Wave Generation Power Plant. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 234, 118–133. [Google Scholar] [CrossRef]
- M’zoughi, F.; Bouallègue, S.; Garrido, A.J.; Garrido, I.; Ayadi, M. Fuzzy gain scheduled PI-based airflow control of an oscillating water column in wave power generation plants. IEEE J. Ocean. Eng. 2019, 44, 1058–1076. [Google Scholar] [CrossRef]
- Falcão, A.F.O.; Gato, L.M.C. Air Turbines. In Comprehensive Renewable Energy; Sayigh, A., Ed.; 8: Ocean Energy; Elsevier: Oxford, UK, 2012; pp. 111–149. [Google Scholar]
- López, I.; Andreu, J.; Ceballos, S.; de Alegría, I.M.; Kortabarria, I. Review of wave energy technologies and the necessary power-equipment. Renew. Sustain. Energy Rev. 2013, 27, 413–434. [Google Scholar] [CrossRef]
- Setoguchi, T.; Takao, M. Current status of self rectifying air turbines for wave energy conversion. Energy Convers. Manag. 2006, 47, 2382–2396. [Google Scholar] [CrossRef]
- Muller, S.; Diecke, M.; De Donker, R.W. Doubly fed induction generator systems for wind turbines. IEEE Ind. Appl. Mag. 2002, 8, 26–33. [Google Scholar] [CrossRef]
- Ledesma, P.; Usaola, J. Doubly fed induction generator model for transient stability analysis. IEEE Trans. Energy Convers. 2005, 20, 388–397. [Google Scholar] [CrossRef]
- M’zoughi, F.; Garrido, A.J.; Garrido, I.; Bouallègue, S.; Ayadi, M. Sliding Mode Rotational Speed Control of an Oscillating Water Column-based Wave Generation Power Plants. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 1263–1270. [Google Scholar]
- Simpson, M.R. Discharge Measurements Using a Broad-Band Acoustic Doppler Current Profiler; US Department of the Interior, US Geological Survey: Reston, CA, USA, 2001.
- Brumley, B.H.; Cabrera, R.G.; Deines, K.L.; Terray, E.A. Performance of a broad-band acoustic Doppler current profiler. IEEE J. Ocean. Eng. 1991, 16, 402–407. [Google Scholar] [CrossRef]
- Pedersen, T.; Nylund, S.; Dolle, A. Wave height measurements using acoustic surface tracking. In Proceedings of the OCEANS’02 MTS/IEEE, Mississippi, MN, USA, 29–31 October 2002; Volume 3, pp. 1747–1754. [Google Scholar]
- Pedersen, T.; Siegel, E.; Wood, J. Directional wave measurements from a subsurface buoy with an acoustic wave and current profiler (AWAC). In Proceedings of the OCEANS 2007, Vancouver, BC, Canada, 29 September–4 October 2007; pp. 1–10. [Google Scholar]
- Lohrmann, A.; Pedersen, T.K.; Nortek, A.S. System and Method for Determining Directional and Non-Directional Fluid Wave and Current Measurements. U.S. Patent 7,352,651, 1 April 2008. [Google Scholar]
- Work, P.A. Nearshore directional wave measurements by surface-following buoy and acoustic Doppler current profiler. Ocean Eng. 2008, 35, 727–737. [Google Scholar] [CrossRef]
- Sheela, K.G.; Deepa, S.N. Review on methods to fix number of hidden neurons in neural networks. Math. Probl. Eng. 2013. [Google Scholar] [CrossRef] [Green Version]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef]
- Wilamowski, B.M.; Yu, H. Improved computation for Levenberg–Marquardt training. IEEE Trans. Neural Netw. 2010, 21, 930–937. [Google Scholar] [CrossRef]
- Suratgar, A.A.; Tavakoli, M.B.; Hoseinabadi, A. Modified Levenberg–Marquardt method for neural networks training. Int. J. Comput. Inf. Eng. 2010, 6, 46–48. [Google Scholar]
- Ampazis, N.; Perantonis, S.J. Levenberg–Marquardt algorithm with adaptive momentum for the efficient training of feedforward networks. In Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks, Como, Italy, 24–27 July 2000; pp. 126–131. [Google Scholar]













| Capture Chamber | Wells Turbine | DFIG Generator | |
|---|---|---|---|
| = 4.5 m | n = 5 | = 0.5968 Ω | = 18.45 kW |
| = 4.3 m | b = 0.21 m | = 0.6258 Ω | = 400 V |
| = 1.19 | l = 0.165 m | = 0.0003495 H | = 50 Hz |
| = 1029 | r = 0.375 m | = 0.324 H | |
| a = 0.4417 | = 0.324 H | ||
| Network Structure | Epochs | MSE | Network Structure | Epochs | MSE |
|---|---|---|---|---|---|
| 11 | 1.1196 | 237 | 1.0463 × 10 | ||
| 2 × 2 × 1 | 20 | 8.0244 × 10 | 2 × 2 × 2 × 1 | 453 | 9.8214 × 10 |
| 56 | 7.3278 × 10 | 619 | 8.1576 × 10 | ||
| 98 | 3.8778 × 10 | 862 | 8.6248 × 10 | ||
| 68 | 1.5626 × 10 | 202 | 8.5032 × 10 | ||
| 2 × 4 × 1 | 122 | 9.0921 × 10 | 2 × 4 × 2 × 1 | 534 | 7.9368 × 10 |
| 566 | 6.6619 × 10 | 811 | 8.2294 × 10 | ||
| 698 | 4.2215 × 10 | 1000 | 7.6146 × 10 | ||
| 188 | 4.2318 × 10 | 115 | 9.0408 × 10 | ||
| 2 × 8 × 1 | 528 | 5.4049 × 10 | 2 × 2 × 4 × 1 | 482 | 7.7924 × 10 |
| 706 | 7.6852 × 10 | (ANN1) | 726 | 8.1396 × 10 | |
| 1000 | 2.3425 × 10 | 1000 | 6.4947 × 10 | ||
| 307 | 1.7154 × 10 | 98 | 8.3164 × 10 | ||
| 2 × 16 × 1 | 423 | 1.3220 × 10 | 2 × 4 × 4 × 1 | 137 | 6.9595 × 10 |
| 775 | 7.3013 × 10 | (ANN2) | 546 | 8.0274 × 10 | |
| 1000 | 8.8384 × 10 | 934 | 7.0812 × 10 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
M'zoughi, F.; Garrido, I.; Garrido, A.J.; De La Sen, M. ANN-Based Airflow Control for an Oscillating Water Column Using Surface Elevation Measurements. Sensors 2020, 20, 1352. https://doi.org/10.3390/s20051352
M'zoughi F, Garrido I, Garrido AJ, De La Sen M. ANN-Based Airflow Control for an Oscillating Water Column Using Surface Elevation Measurements. Sensors. 2020; 20(5):1352. https://doi.org/10.3390/s20051352
Chicago/Turabian StyleM'zoughi, Fares, Izaskun Garrido, Aitor J. Garrido, and Manuel De La Sen. 2020. "ANN-Based Airflow Control for an Oscillating Water Column Using Surface Elevation Measurements" Sensors 20, no. 5: 1352. https://doi.org/10.3390/s20051352







