Joint Sensor Selection and Power Allocation Algorithm for Multiple-Target Tracking of Unmanned Cluster Based on Fuzzy Logic Reasoning
Abstract
:1. Introduction
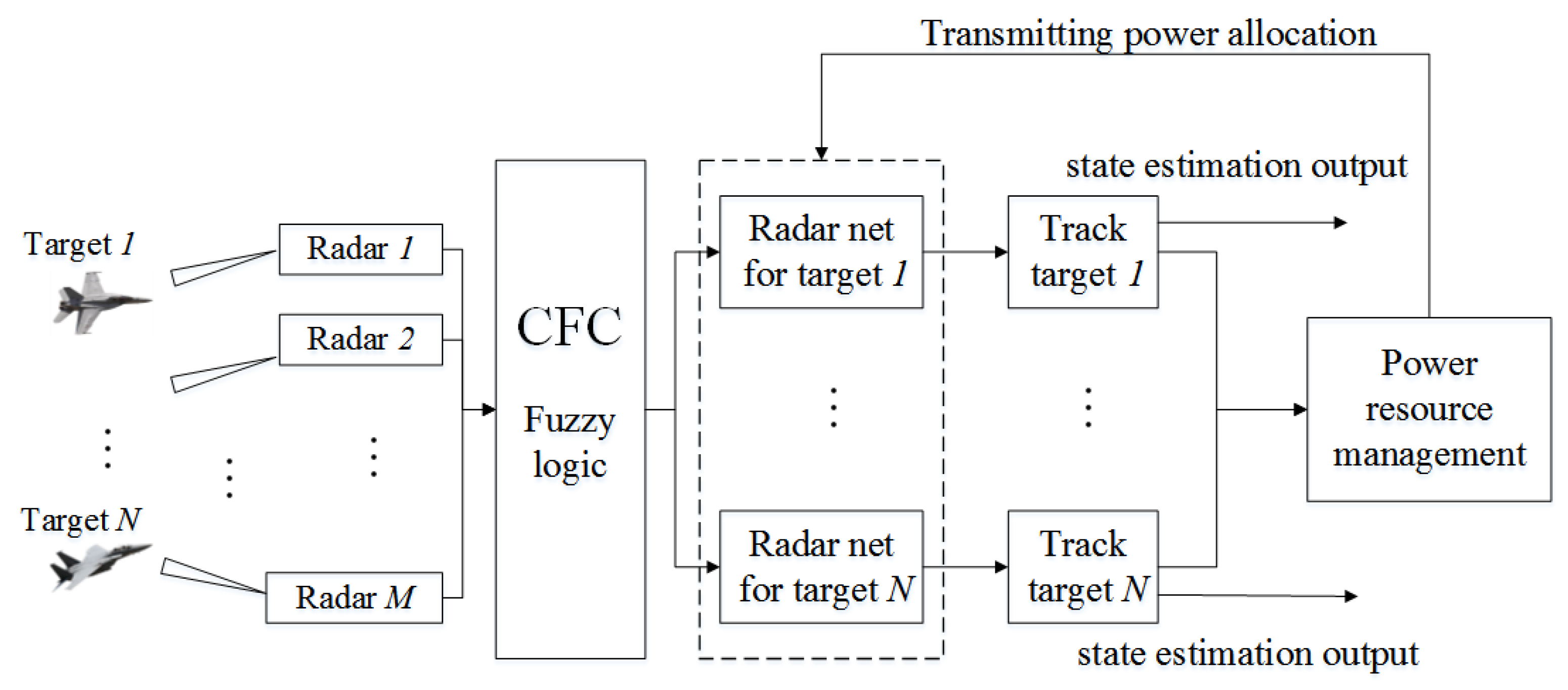
2. System Structure
2.1. Target Motion Model
2.2. Measurement Model
2.3. Fusion Center
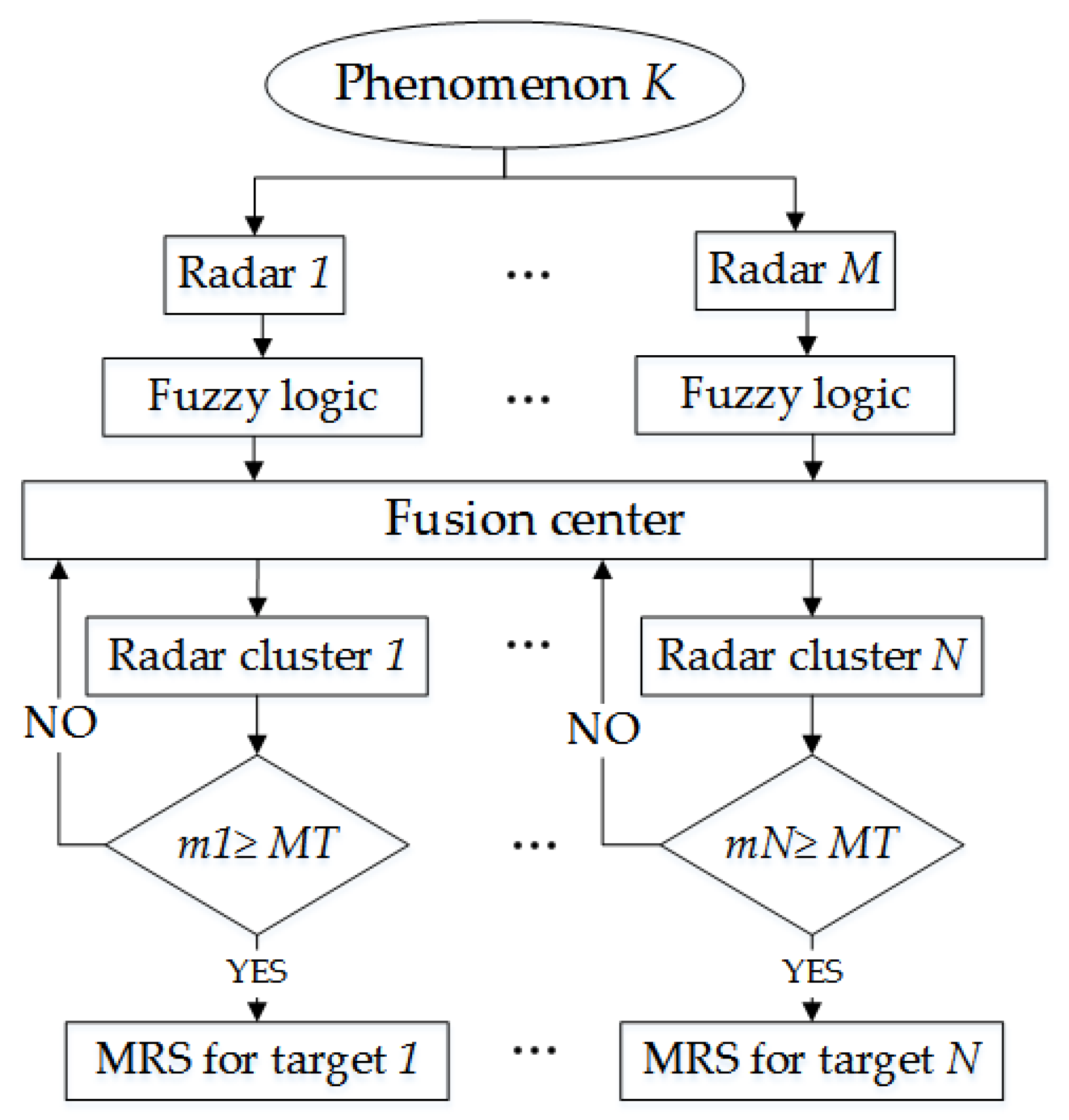
3. Radar Cluster
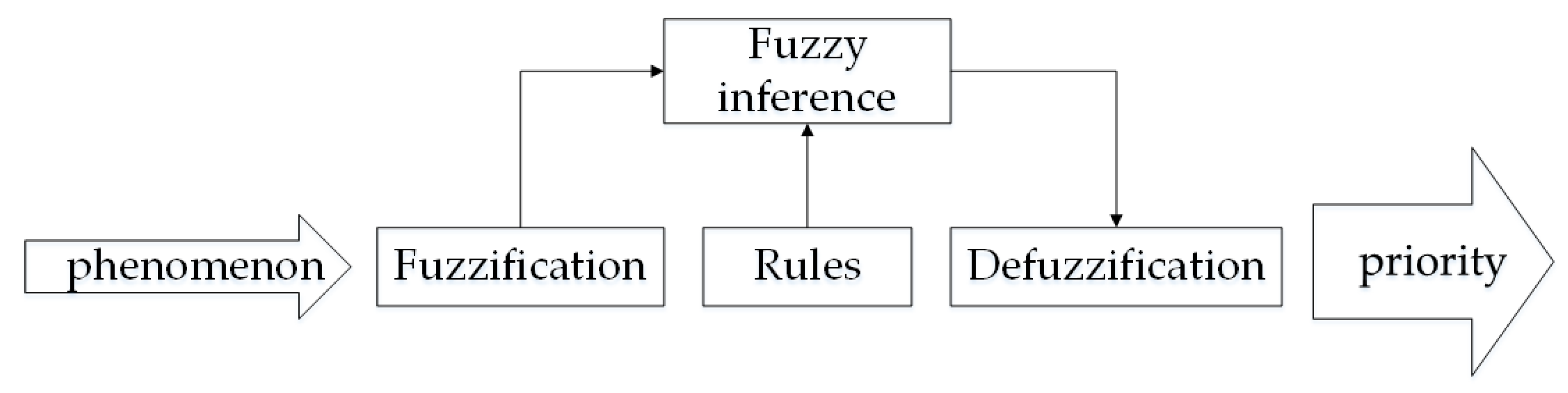
3.1. Target Priority Based on Fuzzy Logic Reasoning
3.1.1. Fuzzification
3.1.2. Fuzzy Rule
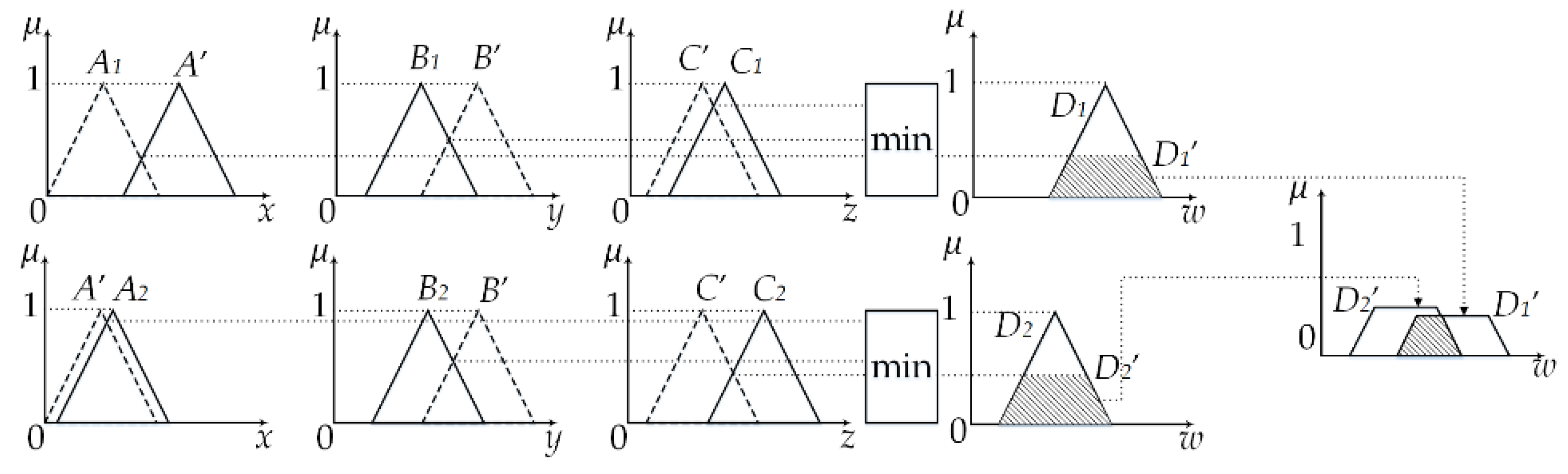
3.1.3. Fuzzy Inference
3.1.4. Defuzzification
3.2. Radar Clustering Strategy Based on the Target Priority
- Select the highest priority value from the matrix . Then the radar mk corresponding to is assigned to the radar cluster that will track the target nk. Set all values of the matrix in line mk to zeros.
- Repeat step 1 to assign radars to each target. If the number of radars assigned to a target has reached the preset require number MT, set all values in the column of the target in matrix to 0. Figure 5 shows the flow of radar clustering algorithm.
4. Management of Power Resource of Radar Networks
4.1. BCRLB of Target Tracking
4.2. Power Resource Management Opportunity Constraint Programming Model
4.3. Model Solving Method
4.3.1. Stochastic Simulation
| Algorithm 1. Stochastic simulation algorithm |
| Step (1): Let . |
| Step (2): Generate N sets of RCS vector samples from sample space . |
| Step (3): If , then . Repeat steps 2 to 3. |
| Step (4): Let . |
| Step (5): If , then satisfies the confidence level , otherwise it does not. |
4.3.2. Hybrid Intelligent Algorithm
| Algorithm 2. Stochastic simulation algorithm |
| Step (1): According to the target motion equation under zero process noise, predict the state vector at the moment;. |
| Step (2): Initialize population S and stain length N, then verify the feasibility of chromosomes using random simulation. |
| Step (3): Hybridize and mutate chromosomes, use random simulation to verify whether the chromosomes meet the constraints, and correct those chromosomes that do not meet the constraints. |
| Step (4): Calculate the objective function value of all chromosomes, and calculate the fitness function value of each stain according to the objective function value. |
| Step (5): Use roulette to select chromosomes. If the requirements of the stopping rules are not met, go to (3). If the stopping rules are met, go to step (6). |
| Step (6): Returns the best chromosome as the optimal radar transmit power . |
5. Target State Estimation
| Algorithm 3. UKF algorithm |
| Step (1): Let k = 1, initialize each radar transmit power , target state and covariance matrix . |
| Step (2): The transmitting power of each radar is , get the measured value of the target, and calculate . |
| Step (3): Construct the 2L + 1 sigma point set and the weights corresponding to the point set according to the following formula. Where, is a scale factor, represents the ith column of the square root of the matrix; I represents the dimension of the state vector. |
| Step (4): Map the sigma point set to the predicted point set through the state transition function , and calculate the new target state and variance by weighting. |
| Step (5): Map the sigma prediction point set to the new point set through the measurement equation, and calculate the mean , variance and . |
| Step (6): Calculate the gain matrix and update and covariance matrix with the gain matrix. |
| Step (7): According to the intelligent hybrid algorithm proposed above, predict the radar transmission power at the kth moment, let and then jump to step (2) |
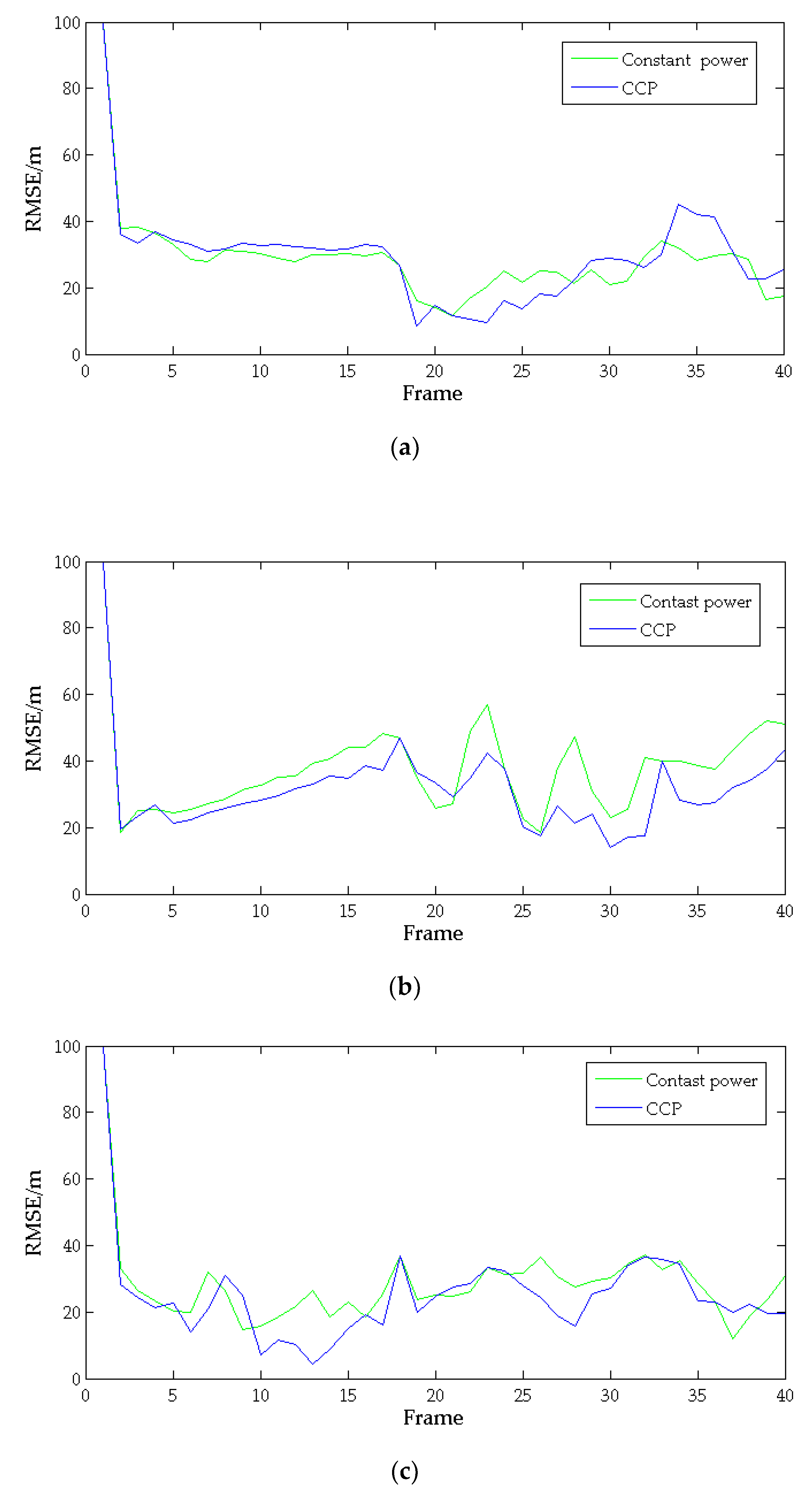
6. Simulation Results and Analysis
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- IF (range is close) AND (speed is very slow) AND (identity is low risk), then (priority is Medium)
- IF (range is close) AND (speed is very slow) AND (identity is medium risk), then (priority is High)
- IF (range is close) AND (speed is very slow) AND (identity is high risk), then (priority is High)
- IF (range is close) AND (speed is slow) AND (identity is low risk), then (priority is Medium)
- IF (range is close) AND (speed is slow) AND (identity is medium risk), then (priority is High)
- IF (range is close) AND (speed is slow) AND (identity is high risk), then (priority is High)
- IF (range is close) AND (speed is medium) AND (identity is low risk), then (priority is Medium)
- IF (range is close) AND (speed is medium) AND (identity is medium risk), then (priority is High)
- IF (range is close) AND (speed is medium) AND (identity is high risk), then (priority is High)
- IF (range is close) AND (speed is fast) AND (identity is low risk), then (priority is High)
- IF (range is close) AND (speed is fast) AND (identity is medium risk), then (priority is High)
- IF (range is close) AND (speed is fast) AND (identity is high risk), then (priority is High)
- IF (range is close) AND (speed is very fast) AND (identity is low risk), then (priority is High)
- IF (range is close) AND (speed is very fast) AND (identity is medium risk), then (priority is High)
- IF (range is close) AND (speed is very fast) AND (identity is high risk), then (priority is High)
- IF (range is medium-close) AND (speed is very slow) AND (identity is low risk), then (priority is Medium)
- IF (range is medium-close) AND (speed is very slow) AND (identity is medium risk), then (priority is Medium)
- IF (range is medium-close) AND (speed is very slow) AND (identity is high risk), then (priority is Medium)
- IF (range is medium-close) AND (speed is slow) AND (identity is low risk), then (priority is Medium)
- IF (range is medium-close) AND (speed is slow) AND (identity is medium risk), then (priority is Medium)
- IF (range is medium-close) AND (speed is slow) AND (identity is high risk), then (priority is High)
- IF (range is medium-close) AND (speed is medium) AND (identity is low risk), then (priority is Medium)
- IF (range is medium-close) AND (speed is medium) AND (identity is medium risk), then (priority is Medium)
- IF (range is medium-close) AND (speed is medium) AND (identity is high risk), then (priority is High)
- IF (range is medium-close) AND (speed is fast) AND (identity is low risk), then (priority is Medium)
- IF (range is medium-close) AND (speed is fast) AND (identity is medium risk), then (priority is High)
- IF (range is medium-close) AND (speed is fast) AND (identity is high risk), then (priority is High)
- IF (range is medium-close) AND (speed is very fast) AND (identity is low risk), then (priority is Medium)
- IF (range is medium-close) AND (speed is very fast) AND (identity is medium risk), then (priority is High)
- IF (range is medium-close) AND (speed is very fast) AND (identity is high risk), then (priority is High)
- IF (range is medium) AND (speed is very slow) AND (identity is low risk), then (priority is Low)
- IF (range is medium) AND (speed is very slow) AND (identity is medium risk), then (priority is Medium)
- IF (range is medium) AND (speed is very slow) AND (identity is high risk), then (priority is Medium)
- IF (range is medium) AND (speed is slow) AND (identity is low risk), then (priority is Low)
- IF (range is medium) AND (speed is slow) AND (identity is medium risk), then (priority is Medium)
- IF (range is medium) AND (speed is slow) AND (identity is high risk), then (priority is Medium)
- IF (range is medium) AND (speed is medium) AND (identity is low risk), then (priority is Medium)
- IF (range is medium) AND (speed is medium) AND (identity is medium risk), then (priority is Medium)
- IF (range is medium) AND (speed is medium) AND (identity is high risk), then (priority is Medium)
- IF (range is medium) AND (speed is fast) AND (identity is low risk), then (priority is Medium)
- IF (range is medium) AND (speed is fast) AND (identity is medium risk), then (priority is Medium)
- IF (range is medium) AND (speed is fast) AND (identity is high risk), then (priority is High)
- IF (range is medium) AND (speed is very fast) AND (identity is low risk), then (priority is Medium)
- IF (range is medium) AND (speed is very fast) AND (identity is medium risk), then (priority is Medium)
- IF (range is medium) AND (speed is very fast) AND (identity is high risk), then (priority is High)
- IF (range is medium-far) AND (speed is very slow) AND (identity is low risk), then (priority is Low)
- IF (range is medium-far) AND (speed is very slow) AND (identity is medium risk), then (priority is Low)
- IF (range is medium-far) AND (speed is very slow) AND (identity is high risk), then (priority is Medium)
- IF (range is medium-far) AND (speed is slow) AND (identity is low risk), then (priority is Low)
- IF (range is medium-far) AND (speed is slow) AND (identity is medium risk), then (priority is Low)
- IF (range is medium-far) AND (speed is slow) AND (identity is high risk), then (priority is Medium)
- IF (range is medium-far) AND (speed is medium) AND (identity is low risk), then (priority is Low)
- IF (range is medium-far) AND (speed is medium) AND (identity is medium risk), then (priority is Low)
- IF (range is medium-far) AND (speed is medium) AND (identity is high risk), then (priority is Medium)
- IF (range is medium-far) AND (speed is fast) AND (identity is low risk), then (priority is Low)
- IF (range is medium-far) AND (speed is fast) AND (identity is medium risk), then (priority is Medium)
- IF (range is medium-far) AND (speed is fast) AND (identity is high risk), then (priority is Medium)
- IF (range is medium-far) AND (speed is very fast) AND (identity is low risk), then (priority is Low)
- IF (range is medium-far) AND (speed is very fast) AND (identity is medium risk), then (priority is Medium)
- IF (range is medium-far) AND (speed is very fast) AND (identity is high risk), then (priority is Medium)
- IF (range is far) AND (speed is very slow) AND (identity is low risk), then (priority is Low)
- IF (range is far) AND (speed is very slow) AND (identity is medium risk), then (priority is Low)
- IF (range is far) AND (speed is very slow) AND (identity is high risk), then (priority is Medium)
- IF (range is far) AND (speed is slow) AND (identity is low risk), then (priority is Low)
- IF (range is far) AND (speed is slow) AND (identity is medium risk), then (priority is Low)
- IF (range is far) AND (speed is slow) AND (identity is high risk), then (priority is Medium)
- IF (range is far) AND (speed is medium) AND (identity is low risk), then (priority is Low)
- IF (range is far) AND (speed is medium) AND (identity is medium risk), then (priority is Low)
- IF (range is far) AND (speed is medium) AND (identity is high risk), then (priority is Medium)
- IF (range is far) AND (speed is fast) AND (identity is low risk) then (priority is Low)
- IF (range is far) AND (speed is fast) AND (identity is medium risk), then (priority is Low)
- IF (range is far) AND (speed is fast) AND (identity is high risk), then (priority is Medium)
- IF (range is far) AND (speed is very fast) AND (identity is low risk), then (priority is Low)
- IF (range is far) AND (speed is very fast) AND (identity is medium risk), then (priority is Low)
- IF (range is far) AND (speed is very fast) AND (identity is high risk), then (priority is Medium)
References
- Huang, H.; Bai, J.; Zhou, H. Present situation and key technologies of unmanned cooperative operation under intelligent air combat system. Navig. Control. 2019, 18, 15–23. [Google Scholar]
- Jens, K.; Oliver, B.; Delphine, C. UAV detection with MIMO radar. In Proceedings of the 2017 International Radar Symposium (IRS), Prague, Czech Republic, 28–30 June 2017. [Google Scholar]
- Yan, J.; Jiu, B.; Liu, H.; Bao, Z. Joint cluster and power allocation algorithm for multiple targets tracking in multistatic radar systems. J. Electron. Inf. Technol. 2013, 35, 1875–1881. [Google Scholar] [CrossRef]
- Godrich, H.; Petropulu, A.; Poor, H. Sensor selection in distributed multiple-radar architectures for localization: A knapsack problem formulation. IEEE Trans. Signal Process. 2012, 60, 247–260. [Google Scholar] [CrossRef]
- He, Q.; Blum, R.; Godrich, H.; Haimovich, A. Target velocity estimation and antenna placement for MIMO radar with widely separated antennas. IEEE J. Sel. Top. Signal Process. 2010, 4, 79–100. [Google Scholar] [CrossRef]
- Ye, Y.; W, Y.; Kirubarajan, T. Scaled accuracy based power allocation for multi-target tracking with colocated MIMO radars. Signal Process. 2019, 158, 227–240. [Google Scholar]
- Shi, C.; Zhou, J.; Wang, F. LPI based resource management for target tracking in distributed radar network. In Proceedings of the 2016 IEEE Radar Conference, Philadelphia, PA, USA, 2–6 May 2016; pp. 822–826. [Google Scholar]
- Yan, J.; Pu, W.; Zhou, S. Collaborative detection and power allocation framework for target tracking in multiple radar system. Inf. Fusion 2020, 55, 173–183. [Google Scholar] [CrossRef]
- Yan, J.; Liu, H.; Pu, W. Joint beam selection and power allocation for multiple targets tracking in netted collocated MIMO radar system. IEEE Trans. Signal Process. 2016, 64, 6417–6427. [Google Scholar] [CrossRef]
- Andargoli, S.; Malekzadeh, J. Target assignment and power allocation for LPI radar networks. In Proceedings of the International Symposium on Artificial Intelligence and Signal Processing, Mashhad, Iran, 3–5 March 2015; pp. 234–239. [Google Scholar]
- Ma, B.; Chen, H.; Sun, B.; Xiao, H. A joint scheme of antenna selection and power allocation for localization in MIMO radar sensor networks. IEEE Commun. Lett. 2014, 18, 2225–2228. [Google Scholar] [CrossRef]
- Chavali, P.; Nehorai, A. Scheduling and power allocation in a cognitive radar network for multiple-target tracking. IEEE Trans. Signal Process. 2012, 60, 715–729. [Google Scholar] [CrossRef]
- She, J.; Wang, F.; Zhou, J. A novel sensor selection and power allocation algorithm for multiple-target tracking in an LPI radar network. Sensors 2016, 16, 2193. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, Y.; Petropulu, A. A study on power allocation for widely separated CS-based MIMO radar. SPIE Defense, Security, and Sensing. In Proceedings of the International Society for Optical Engineering, Baltimore, MD, USA, 8 June 2012; p. 8365. [Google Scholar]
- Xie, M.; Yi, W.; Kirubarajan, T.; Kong, L. Joint node selection and power allocation strategy for multi-target tracking in decentralized radar networks. IEEE Trans Signal Process. 2018, 66, 729–743. [Google Scholar] [CrossRef]
- Han, Q.; Pan, M.; Liang, Z. Joint power and beam allocation of opportunistic array radar for multiple target tracking in clutter. Digit. Signal Process. 2018, 78, 136–151. [Google Scholar] [CrossRef]
- Han, Q.; Pan, M.; Gong, S.; Long, W. Resource management of opportunistic digital array radar antenna aperture for pattern synthesis. IET Radar Sonar Navig. 2017, 11, 829–837. [Google Scholar] [CrossRef]
- Lewandowski, W.; Azoubib, J.; Klepczynski, W. GPS: Primary tool for time transfer. Proc. IEEE 1999, 87, 163–172. [Google Scholar] [CrossRef]
- Tichavsky, P.; Muravchik, C.; Nehorai, A. Posterior Cramér-Rao bounds for dscrete-time nonlinear filtering. IEEE Trans. Signal Process. 1998, 46, 1386–1396. [Google Scholar] [CrossRef] [Green Version]
- Mamdani, E. Application of fuzzy logic to approximate reasoning using linguistic synthesis. IEEE Tran. Comput. 1977, 26, 1182–1191. [Google Scholar] [CrossRef]
- Klir, G.; Bo, Y. Fuzzy Sets and Fuzzy Logic Theory and Application; Prentice-Hall International: Upper Saddle River, NJ, USA, 1995; p. 6. [Google Scholar]
- Miranda, S.; Baker, C.; Woodbridge, K. Knowledge-based resource management for multifunction radar. IEEE Signal Process. Mag. 2006, 23, 66–76. [Google Scholar] [CrossRef] [Green Version]
- Miranda, S.; Baker, C.; Woodbridge, K. Fuzzy logic approach for prioritisation of radar tasks and sectors of surveillance in multifunction radar. IET Radar, Sonar Navig. 2007, 1, 131–141. [Google Scholar] [CrossRef]
- Wang, L. A Course in Fuzzy Systems and Control; International Edition; Prentice-Hall International: Upper Saddle River, NJ, USA, 1997; pp. 85–86. [Google Scholar]
- Han, Q.; Pan, M.; Zhang, W. Time resource management of OAR based on fuzzy logic priority for multiple target tracking. J. Syst. Eng. Electron. 2018, 29, 742–755. [Google Scholar]
- Glass, J.; Smith, L. MIMO radar resource allocation using posterior Cramer-Rao lower bounds. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011. [Google Scholar]
- Ristic, B.; Arulampalam, S.; Gordon, N. Beyond the Kalman Filter: Particle Filters for Tracking Applications; Artech House: Fitchburg, MA, USA, 2004; pp. 68–70. [Google Scholar]
- Liu, B. Theory and Practice of Uncertain Programming, 1st ed.; Tsinghua University Press: Beijing, China, 2003; pp. 88–89. [Google Scholar]
- Skolnik, M. Introduction to Radar System, 3rd ed.; Tata McGraw-Hill Publishing Company Limited: New Delhi, India, 2001; pp. 313–402. [Google Scholar]






| Fuzzy Variable | Excursion | Fuzzy Value |
|---|---|---|
| range | (0,360] (km) | close, medium-close, medium, medium-far, far |
| speed | (0,960] (m/s) | very slow, slow, medium, fast, very fast |
| target identity | (0,1] | low risk, medium risk, high risk |
| priority | (0,1] | low, medium, high |
| Parameter | Wavelength | Effective Bandwidth | Effective Timewidth | Sampling Interval |
|---|---|---|---|---|
| Value | 0.03 m | 5 MHz | 1 ms | 0.5 s |
| Radar Serial Number | Position/(m, m) |
|---|---|
| 1 | (−82,500, 0) |
| 2 | (−82,500, 55,000) |
| 3 | (−82,500, 110,000) |
| 4 | (−82,500, 165,000) |
| 5 | (−27,500, 0) |
| 6 | (27,500, 0) |
| 7 | (−27,500, 165,000) |
| 8 | (27,500, 165,000) |
| 9 | (82,500, 165,000) |
| 10 | (82,500, 110,000) |
| 11 | (82,500, 55,000) |
| 12 | (82,500, 0) |
| Target | Initial position/(m, m) | Velocity/(m/s) |
|---|---|---|
| 1 | (−40,000, 135,000) | (30, −520) |
| 2 | (31,000, 125,000) | (−310, −660) |
| 3 | (45,500, 29,000) | (90, 530) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Pan, M.; Han, Q. Joint Sensor Selection and Power Allocation Algorithm for Multiple-Target Tracking of Unmanned Cluster Based on Fuzzy Logic Reasoning. Sensors 2020, 20, 1371. https://doi.org/10.3390/s20051371
Zhang Y, Pan M, Han Q. Joint Sensor Selection and Power Allocation Algorithm for Multiple-Target Tracking of Unmanned Cluster Based on Fuzzy Logic Reasoning. Sensors. 2020; 20(5):1371. https://doi.org/10.3390/s20051371
Chicago/Turabian StyleZhang, Yuanshi, Minghai Pan, and Qinghua Han. 2020. "Joint Sensor Selection and Power Allocation Algorithm for Multiple-Target Tracking of Unmanned Cluster Based on Fuzzy Logic Reasoning" Sensors 20, no. 5: 1371. https://doi.org/10.3390/s20051371
APA StyleZhang, Y., Pan, M., & Han, Q. (2020). Joint Sensor Selection and Power Allocation Algorithm for Multiple-Target Tracking of Unmanned Cluster Based on Fuzzy Logic Reasoning. Sensors, 20(5), 1371. https://doi.org/10.3390/s20051371




