Comparison of Spectrum Estimation Methods for the Accurate Evaluation of Sea State Parameters †
Abstract
:1. Introduction
2. Monitoring of Sea State Parameters
3. Spectrum Estimation Methods
3.1. Outline of Some of the Main Spectrum Estimation Methods
3.2. Welch Method
3.3. Thomson Method
3.4. Parametric Estimation Methods (ARMA)
4. Assessment of Sea State Parameters
4.1. Iterative Procedure
4.1.1. Estimation of the Peak Frequency
4.1.2. Estimation of the Peak Enhancement Factor
4.1.3. Estimation of the Significant Wave Height
4.2. Nonlinear Least-Square Method
5. Numerical Study of Selected Test Cases
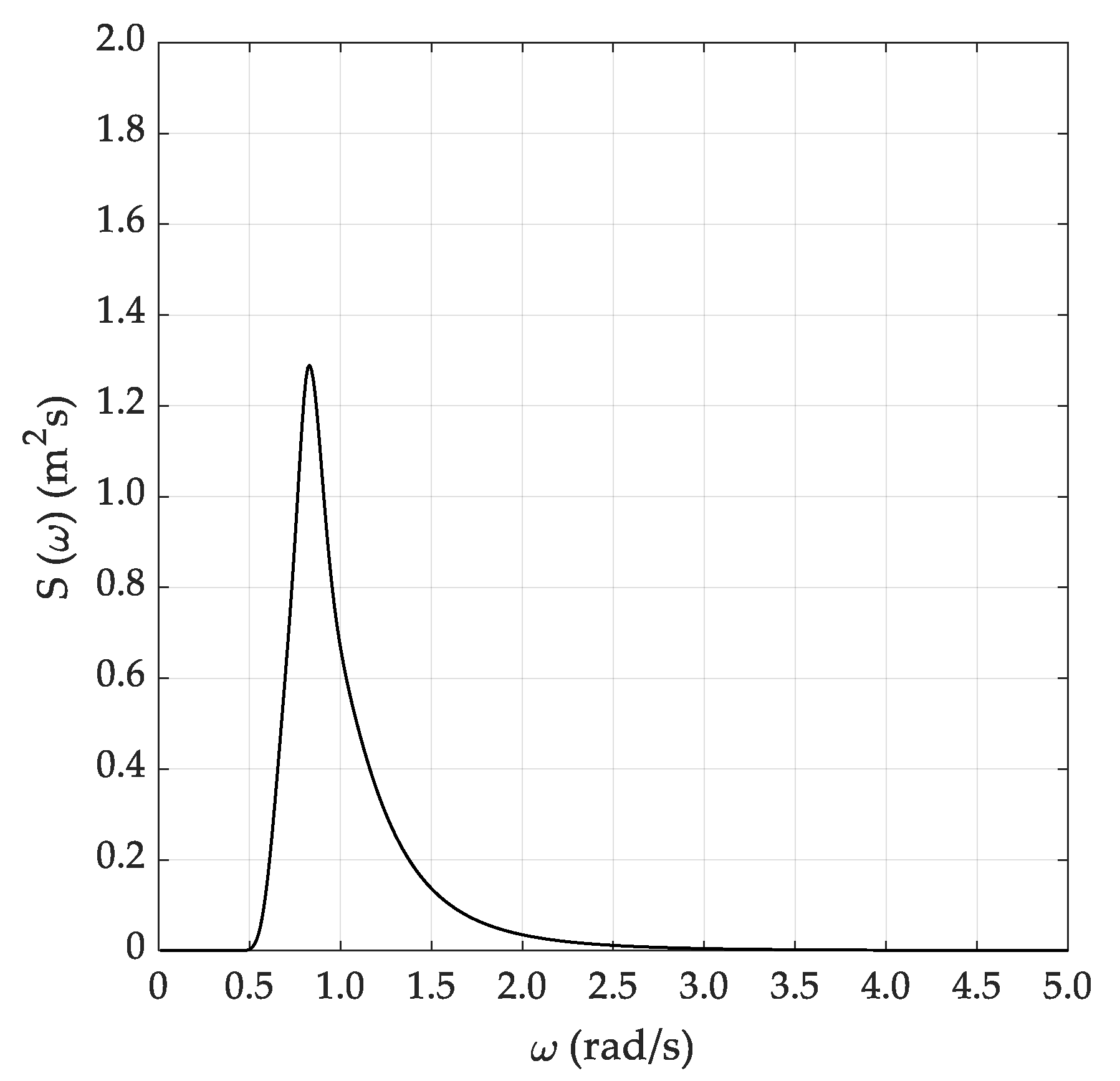
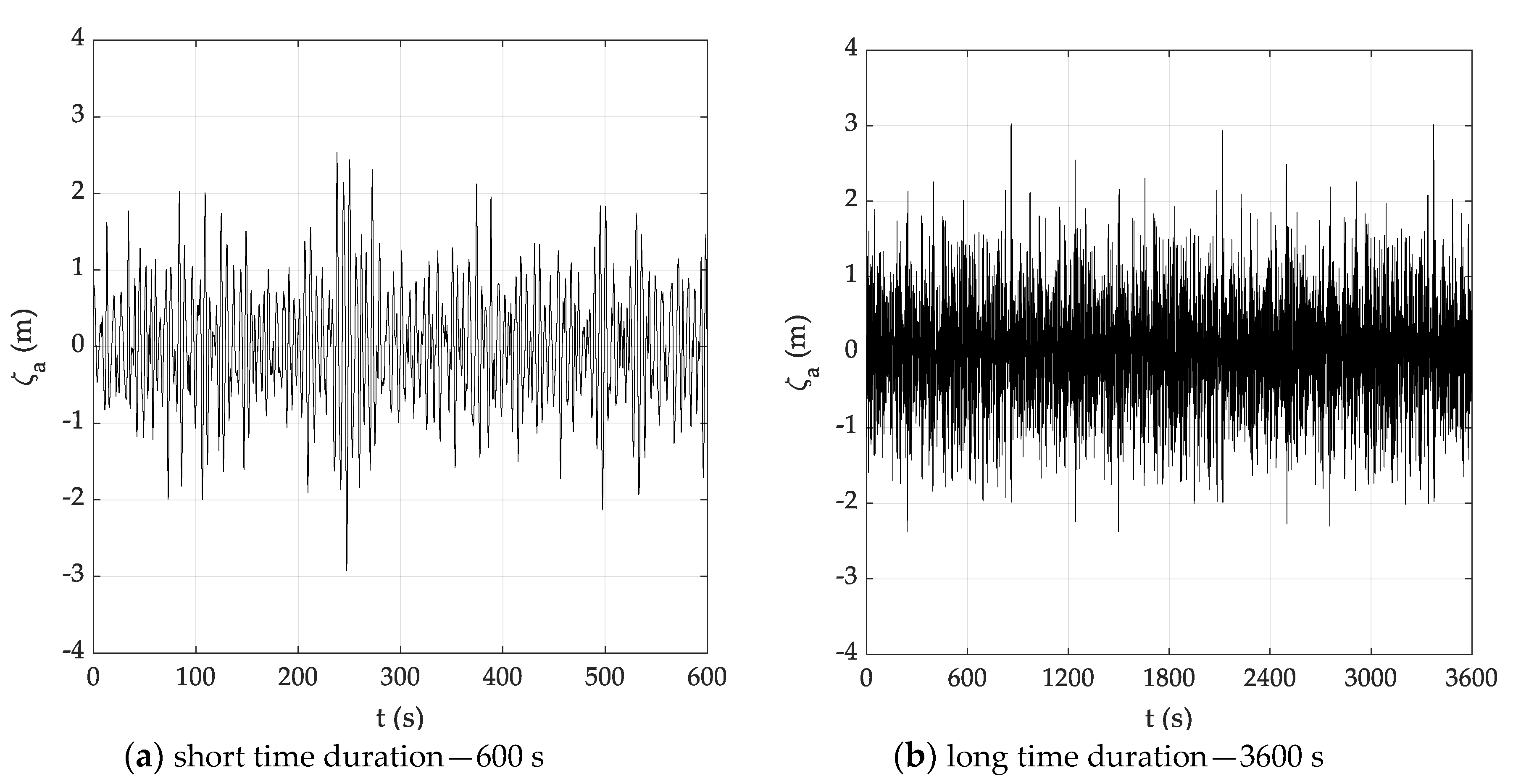
5.1. Selection of Test Cases and Random Wave Generation
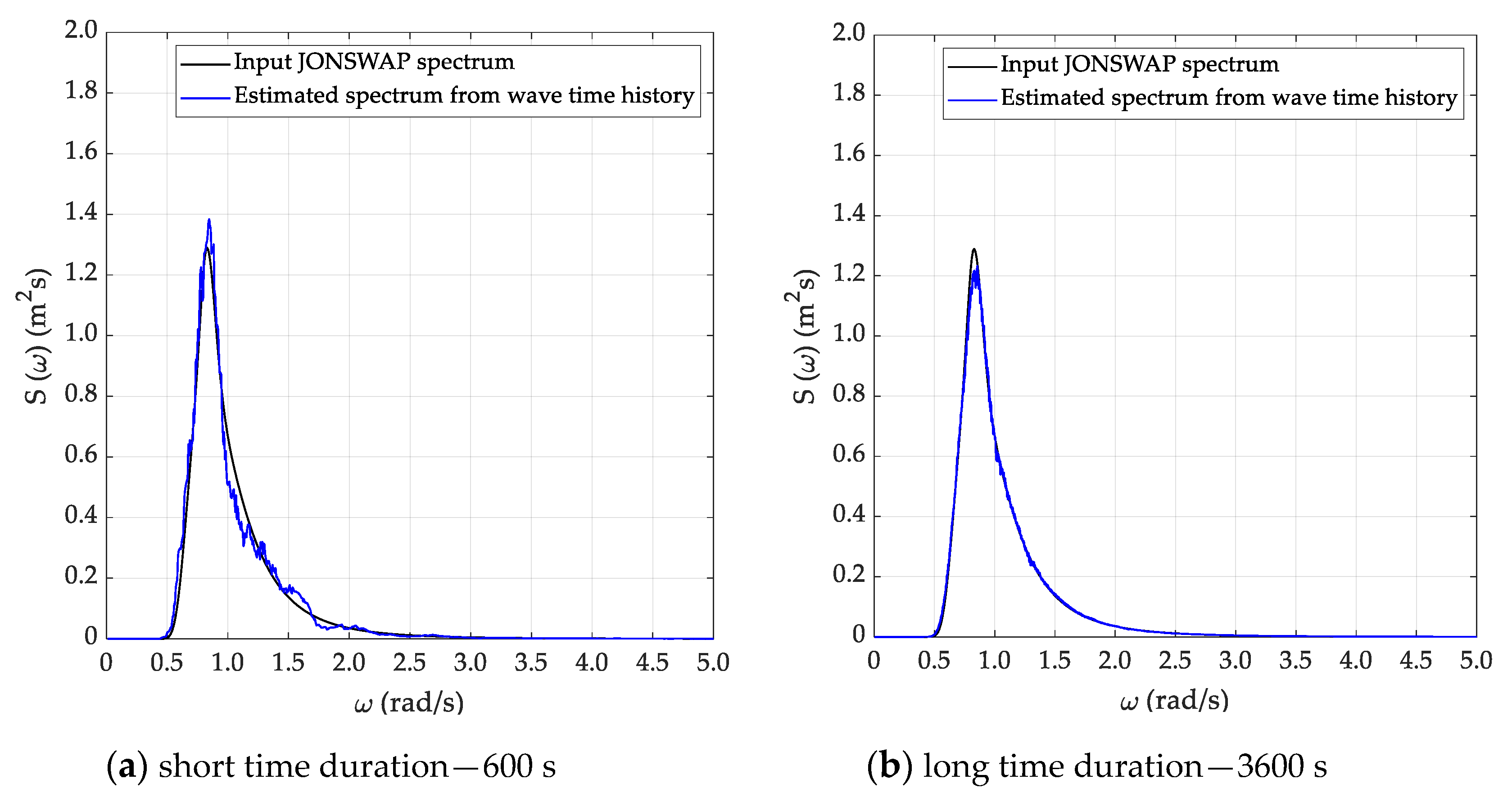
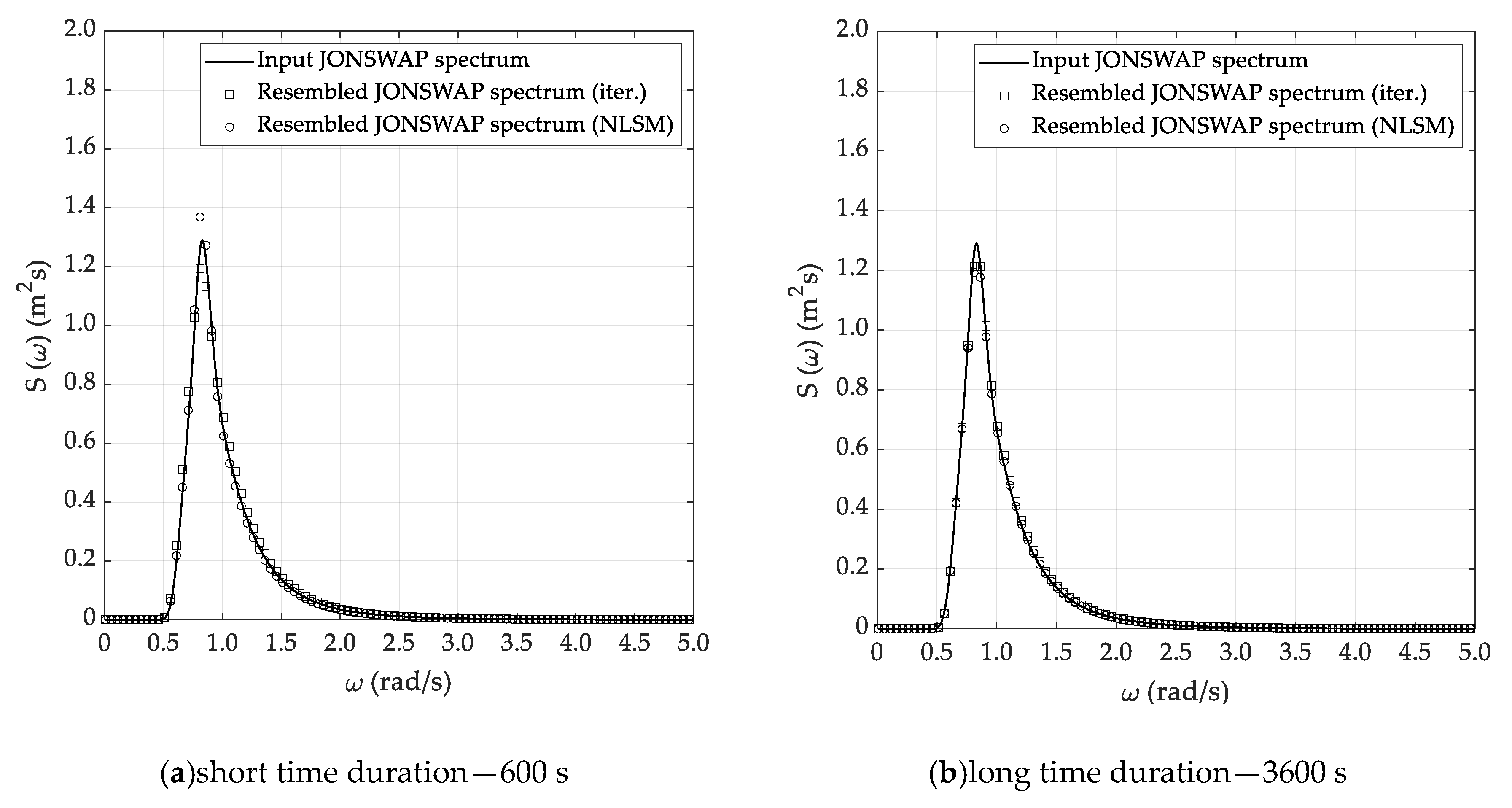
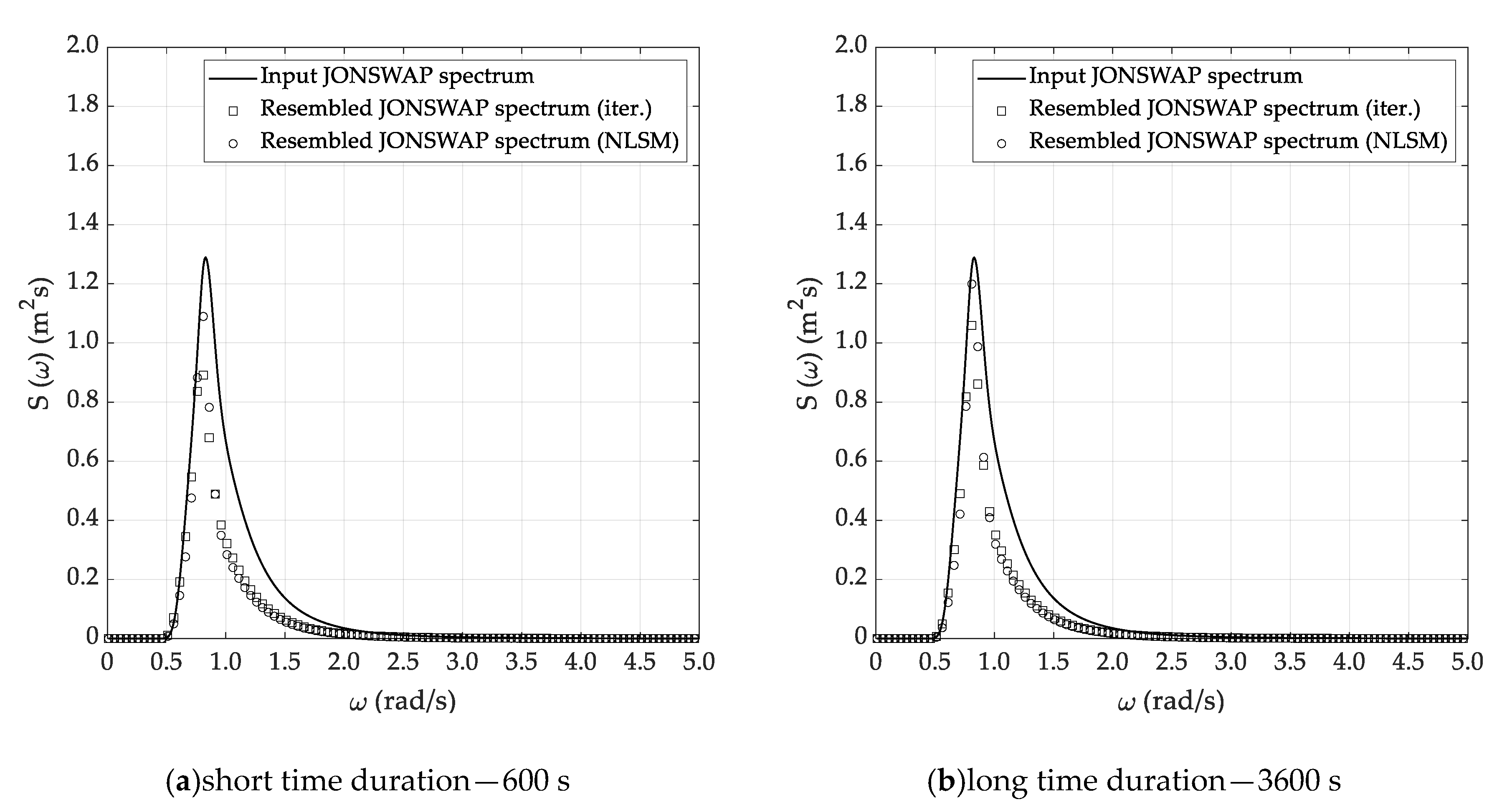
5.2. Spectral Analysis
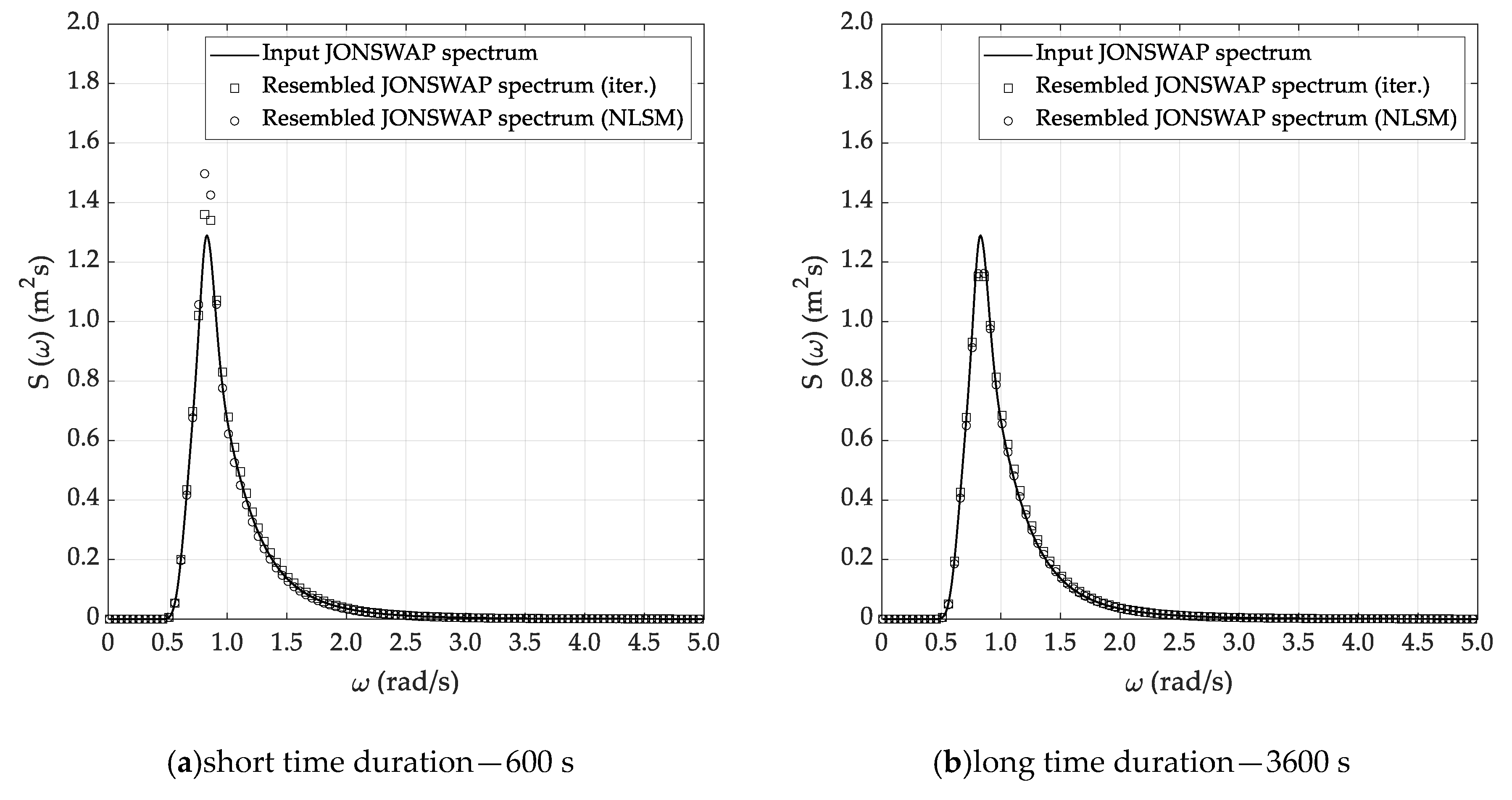
5.3. Sea State Reconstruction
- (i)
- The Welch and Thomson methods allow reconstructing the sea state parameters with relative errors lower than 3% for the significant wave height and mean period and 8% for the peak enhancement factor.
- (ii)
- Higher errors arise if the ARMA method is applied, especially for the assessment of the spectrum peak enhancement factor, with absolute percentage errors up to 50%.
- (iii)
- The accuracy of the methods generally increases with the time duration, even if the reliability of reconstructed parameters is sufficiently accurate for practical purposes, even if the short time history, corresponding to 600 s, is embodied in the spectral analysis. Nevertheless, this trend is not always clear, provided that a certain dependence on both the spectrum estimation method and reconstruction technique is also recognized.
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Piscopo, V.; Scamardella, A. Passenger ship seakeeping optimization by the Overall Motion Sickness Incidence. Ocean Eng. 2014, 76, 86–97. [Google Scholar]
- Mansard, E.P.D.; Funke, E.R. On the fitting of JONSWP spectra to measured sea states. In Proceedings of the 22nd Conference on Coastal Engineering, Delft, The Netherlands, 2–6 July 1990. [Google Scholar]
- Rossi, G.B.; Crenna, F.; Piscopo, V.; Scamardella, A. Data processing for the accurate evaluation of sea-waves parameters. In Proceedings of the IMEKO TC 19 International Workshop on Metrology for the Sea, Genoa, Italy, 3–5 October 2019. [Google Scholar]
- Mansard, E.P.D.; Funke, E.R. On the fitting of parametric models to measured wave spectra. In Proceedings of the 2nd International Symposium on Waves and Coastal Engineering, Hannover, Germany, 12–14 October 1988. [Google Scholar]
- Det Norske Veritas. Environmental Conditions and Environmental Loads; Recommended Practice DNV-RP-C205; Det Norske Veritas: Oslo, Norway, 2010. [Google Scholar]
- Marple, S.L. Digital Spectral Analysis; Prentice—Hall: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Percival, D.B.; Walden, A.T. Spectral Analysis for Physical Applications; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Schuster, A. On the Investigation of Hidden Periodicities with Application to a Supposed 26 Day Period of Meteorological Phenomena. Terr. Magn. 1898, 3, 13–41. [Google Scholar] [CrossRef]
- Welch, P.D. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging over Short Modified Periodograms. IEEE Trans. Audio Electroacoust. 1967, 15, 70–73. [Google Scholar] [CrossRef] [Green Version]
- Thomson, D.J. Spectrum Estimation and Harmonic Analysis. Proc. IEEE 1982, 70, 1055–1096. [Google Scholar] [CrossRef] [Green Version]
- Read, W.W. Time Series Analysis of Wave Records and the Search for Wave Groups. Ph.D. Thesis, James Cook University of North Queensland, Townsville, Australia, 1986. [Google Scholar]
- Battjes, J.A.; van Vledder, G. Verification of Kimura’s Theory for Wave Group Statistics. In Proceedings of the 19th International Conference on Coastal Engineering, Houston, TX, USA, 3–7 September 1984. [Google Scholar]
- Coleman, T.F.; Li, Y. Trust Region Approach for Nonlinear Minimization Subject to Bounds. SIAM J. Optim. 1996, 6, 418–445. [Google Scholar] [CrossRef] [Green Version]
- Walden, A.T.; McCoy, E.J.; Percival, D.B. The effective bandwidth of a multitaper spectral estimator. Biometrika 1995, 82, 201–214. [Google Scholar] [CrossRef]
- Walden, A.T.; McCoy, E.J.; Percival, D.B. The Variance of Multitaper Spectrum Estimates for Real Gaussian Processes. IEEE Trans. Signal Process. 1994, 42, 479–482. [Google Scholar] [CrossRef]
- Holm, S.; Hovem, J.M. Estimation of scalar ocean wave spectra by the Maximum Entropy method. IEEE J. Ocean. Eng. 1979, 4, 76–83. [Google Scholar] [CrossRef]
- Mandal, S.; Witz, J.A.; Lyons, G.Y. Reduced order ARMA spectral estimation of ocean waves. Appl. Ocean Res. 1992, 14, 303–312. [Google Scholar] [CrossRef]




| DG | Sea State Condition | Hs | Tm | Tp | γ |
|---|---|---|---|---|---|
| [m] | [s] | [s] | [—] | ||
| 3 | Slight | 1.00 | 4.00 | 4.82 | 3.00 |
| 4 | Moderate | 2.00 | 5.00 | 6.11 | 2.50 |
| 5 | Rough | 3.00 | 6.00 | 7.59 | 1.50 |
| 6 | Very rough | 5.00 | 9.00 | 11.64 | 1.00 |
| (a) Short Time Duration—600 s. | (b) Long Time Duration—3600 s. | ||||||
|---|---|---|---|---|---|---|---|
| Method/Difference | Hs | Tm | γ | Method/Difference | Hs | Tm | γ |
| [m] | [s] | [—] | [m] | [s] | [—] | ||
| Input data | Input | ||||||
| JONSWAP | 1.000 | 4.000 | 3.000 | JONSWAP | 1.000 | 4.000 | 3.000 |
| Welch method | Welch method | ||||||
| Iterative | 0.995 | 4.110 | 2.927 | Iterative | 1.012 | 3.983 | 2.915 |
| NLSM | 0.985 | 4.055 | 2.794 | NLSM | 1.002 | 3.975 | 2.759 |
| Δiter. (%) | −0.495 | 2.743 | −2.426 | Δiter. (%) | 1.236 | −0.421 | −2.849 |
| ΔNLSM (%) | −1.523 | 1.385 | −6.883 | ΔNLSM (%) | 0.189 | −0.637 | −8.044 |
| Thomson method | Thomson method | ||||||
| Iterative | 0.999 | 4.088 | 3.140 | Iterative | 1.011 | 3.994 | 2.999 |
| NLSM | 0.989 | 4.056 | 2.979 | NLSM | 1.001 | 3.988 | 2.904 |
| Δiter. (%) | −0.058 | 2.212 | 4.665 | Δiter. (%) | 1.092 | −0.143 | −0.046 |
| ΔNLSM (%) | −1.058 | 1.412 | −0.702 | ΔNLSM (%) | 0.059 | −0.289 | −3.188 |
| ARMA method | ARMA method | ||||||
| Iterative | 1.024 | 3.979 | 4.000 | Iterative | 0.783 | 3.788 | 1.517 |
| NLSM | 1.015 | 3.920 | 3.084 | NLSM | 0.773 | 3.995 | 4.303 |
| Δiter. (%) | 2.439 | −0.520 | 33.339 | Δiter. (%) | −21.696 | −5.296 | −49.446 |
| ΔNLSM (%) | 1.526 | −1.990 | 2.806 | ΔNLSM (%) | −22.733 | −0.137 | 43.437 |
| (a) Short Time Duration–600 s | (b) Long Time Duration–3600 s | ||||||
|---|---|---|---|---|---|---|---|
| Method/Difference | Hs | Tm | γ | Method/Difference | Hs | Tm | γ |
| [m] | [s] | [—] | [m] | [s] | [—] | ||
| Input data | Input | ||||||
| JONSWAP | 2.000 | 5.000 | 2.500 | JONSWAP | 2.000 | 5.000 | 2.500 |
| Welch method | Welch method | ||||||
| Iterative | 1.876 | 4.684 | 1.491 | Iterative | 2.031 | 4.997 | 2.439 |
| NLSM | 1.851 | 4.789 | 1.262 | NLSM | 2.009 | 5.001 | 2.466 |
| Δiter. (%) | −6.207 | −6.314 | −40.364 | Δiter. (%) | 1.569 | −0.061 | −2.420 |
| ΔNLSM (%) | −7.456 | −4.222 | −49.535 | ΔNLSM (%) | 0.436 | 0.030 | −1.359 |
| Thomson method | Thomson method | ||||||
| Iterative | 1.863 | 4.766 | 1.370 | Iterative | 2.026 | 4.989 | 2.444 |
| NLSM | 1.837 | 4.799 | 1.268 | NLSM | 2.003 | 4.986 | 2.403 |
| Δiter. (%) | −6.865 | −4.678 | −45.214 | Δiter. (%) | 1.298 | −0.215 | −2.241 |
| ΔNLSM (%) | −8.138 | −4.016 | −49.269 | ΔNLSM (%) | 0.169 | −0.271 | −3.892 |
| ARMA method | ARMA method | ||||||
| Iterative | 1.702 | 5.115 | 1.099 | Iterative | 1.887 | 4.872 | 3.006 |
| NLSM | 1.677 | 5.191 | 2.415 | NLSM | 1.868 | 4.808 | 2.078 |
| Δiter. (%) | −14.918 | 2.305 | −56.050 | Δiter. (%) | −5.653 | −2.560 | 20.230 |
| ΔNLSM (%) | −16.154 | 3.824 | −3.407 | ΔNLSM (%) | −6.616 | −3.836 | −16.866 |
| (a) Short Time Duration—600 s | (b) Long Time Duration—3600 s | ||||||
|---|---|---|---|---|---|---|---|
| Method/Difference | Hs | Tm | γ | Method/Difference | Hs | Tm | γ |
| [m] | [s] | [—] | [m] | [s] | [—] | ||
| Input data | Input | ||||||
| JONSWAP | 3.000 | 6.000 | 1.500 | JONSWAP | 3.000 | 6.000 | 1.500 |
| Welch method | Welch method | ||||||
| Iterative | 3.088 | 6.002 | 1.568 | Iterative | 3.018 | 5.920 | 1.309 |
| NLSM | 3.048 | 6.098 | 1.859 | NLSM | 2.976 | 5.940 | 1.391 |
| Δiter. (%) | 2.948 | 0.041 | 4.501 | Δiter. (%) | 0.594 | −1.335 | −12.709 |
| ΔNLSM (%) | 1.598 | 1.629 | 23.95 | ΔNLSM (%) | −0.799 | −1.002 | −7.280 |
| Thomson method | Thomson method | ||||||
| Iterative | 3.058 | 6.005 | 1.251 | Iterative | 3.031 | 5.945 | 1.404 |
| NLSM | 3.015 | 6.082 | 1.618 | NLSM | 2.990 | 5.964 | 1.406 |
| Δiter. (%) | 1.938 | 0.078 | −16.624 | Δiter. (%) | 1.035 | −0.916 | −6.395 |
| ΔNLSM (%) | 0.507 | 1.362 | 7.875 | ΔNLSM (%) | −0.335 | −0.604 | −6.253 |
| ARMA method | ARMA method | ||||||
| Iterative | 2.313 | 6.377 | 1.836 | Iterative | 2.404 | 6.291 | 2.102 |
| NLSM | 2.284 | 6.461 | 2.606 | NLSM | 2.375 | 6.349 | 2.731 |
| Δiter. (%) | −22.902 | 6.279 | 22.370 | Δiter. (%) | −19.872 | 4.858 | 40.153 |
| ΔNLSM (%) | −23.860 | 7.680 | 73.754 | ΔNLSM (%) | −20.819 | 5.813 | 82.040 |
| (a) Short Time Duration—600 s | (b) Long Time Duration—3600 s | ||||||
|---|---|---|---|---|---|---|---|
| Method/Difference | Hs | Tm | γ | Method/Difference | Hs | Tm | γ |
| [m] | [s] | [—] | [m] | [s] | [—] | ||
| Input data | Input | ||||||
| JONSWAP | 5.000 | 9.000 | 1.000 | JONSWAP | 5.000 | 9.000 | 1.000 |
| Welch method | Welch method | ||||||
| Iterative | 4.785 | 8.019 | 1.000 | Iterative | 5.091 | 8.877 | 1.023 |
| NLSM | 4.712 | 8.711 | 1.000 | NLSM | 5.015 | 8.963 | 1.000 |
| Δiter. (%) | −4.297 | −10.905 | 0.000 | Δiter. (%) | 1.814 | −1.363 | 2.320 |
| ΔNLSM (%) | −5.755 | −3.211 | 0.000 | ΔNLSM (%) | 0.309 | −0.406 | 0.000 |
| Thomson method | Thomson method | ||||||
| Iterative | 4.829 | 8.281 | 1.000 | Iterative | 5.094 | 8.995 | 1.000 |
| NLSM | 4.756 | 8.781 | 1.000 | NLSM | 5.017 | 8.995 | 1.000 |
| Δiter. (%) | −3.416 | −7.993 | 0.000 | Δiter. (%) | 1.876 | −0.051 | 0.000 |
| ΔNLSM (%) | −4.887 | −2.429 | 0.000 | ΔNLSM (%) | 0.349 | −0.058 | 0.000 |
| ARMA method | ARMA method | ||||||
| Iterative | 3.206 | 9.560 | 1.574 | Iterative | 3.848 | 9.546 | 3.443 |
| NLSM | 3.164 | 9.720 | 2.535 | NLSM | 3.811 | 9.479 | 3.237 |
| Δiter. (%) | −35.882 | 6.223 | 57.404 | Δiter. (%) | −23.046 | 6.065 | 244.252 |
| ΔNLSM (%) | −36.721 | 7.997 | 153.467 | ΔNLSM (%) | −23.784 | 5.320 | 223.686 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossi, G.B.; Crenna, F.; Piscopo, V.; Scamardella, A. Comparison of Spectrum Estimation Methods for the Accurate Evaluation of Sea State Parameters. Sensors 2020, 20, 1416. https://doi.org/10.3390/s20051416
Rossi GB, Crenna F, Piscopo V, Scamardella A. Comparison of Spectrum Estimation Methods for the Accurate Evaluation of Sea State Parameters. Sensors. 2020; 20(5):1416. https://doi.org/10.3390/s20051416
Chicago/Turabian StyleRossi, Giovanni Battista, Francesco Crenna, Vincenzo Piscopo, and Antonio Scamardella. 2020. "Comparison of Spectrum Estimation Methods for the Accurate Evaluation of Sea State Parameters" Sensors 20, no. 5: 1416. https://doi.org/10.3390/s20051416
APA StyleRossi, G. B., Crenna, F., Piscopo, V., & Scamardella, A. (2020). Comparison of Spectrum Estimation Methods for the Accurate Evaluation of Sea State Parameters. Sensors, 20(5), 1416. https://doi.org/10.3390/s20051416








