Partial Discharge Localization Using Time Reversal: Application to Power Transformers
Abstract
:1. Introduction
2. Methodology
2.1. Principle of Electromagnetic Time Reversal
- (i)
- The electromagnetic or acoustic waves from the source or sources are measured or calculated (forward-time) at one or multiple locations.
- (ii)
- The acquired waveforms are time-reversed and back-injected into the solution medium, using numerical simulations (backward-time).
- (iii)
- A criterion to detect and locate the source(s) is applied within the backward-time phase, such as the maximum amplitude of the total wave, its maximum energy, entropy, etc., to obtain the focal spot.
2.2. Mathematical Derivation
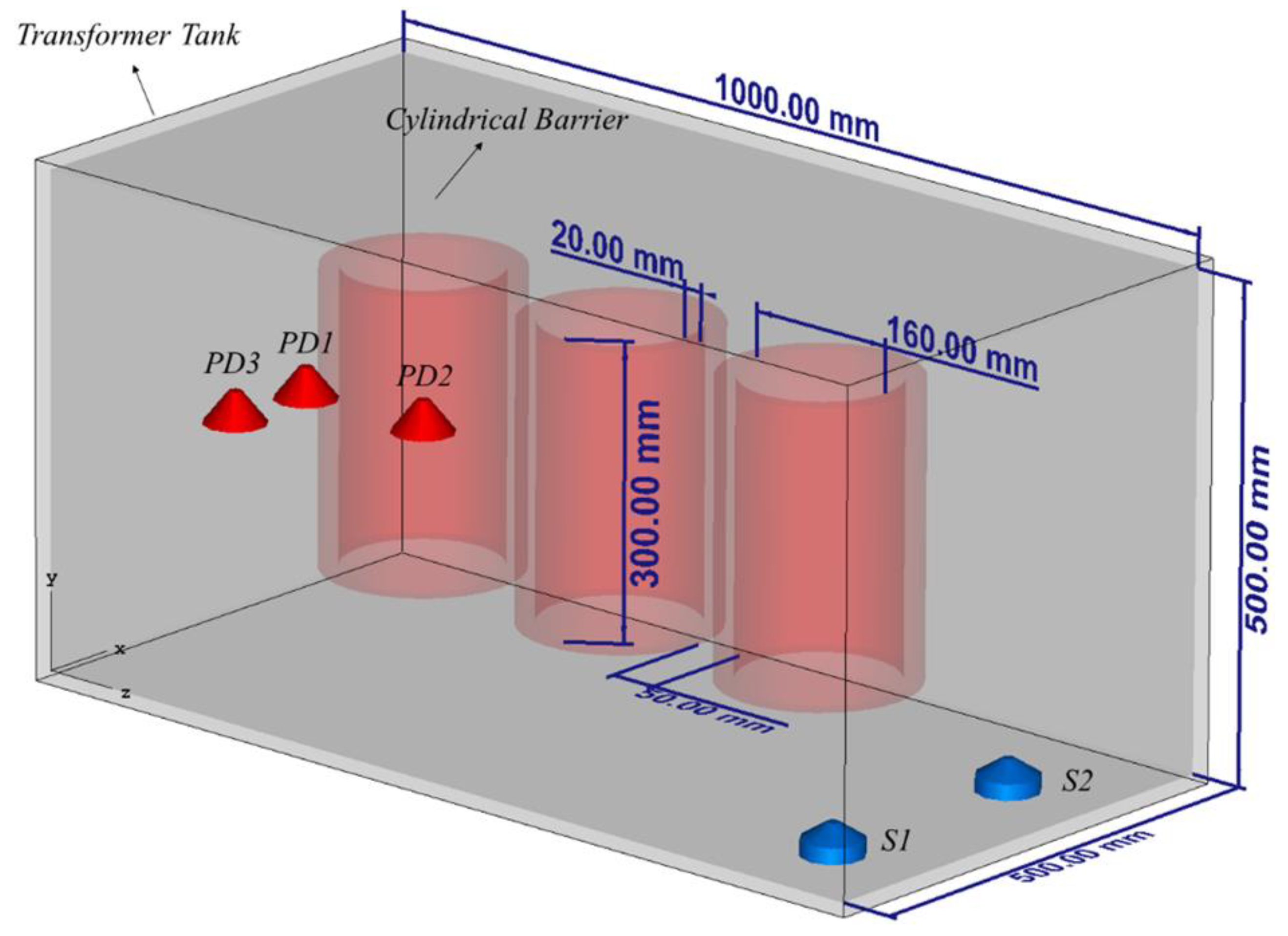
2.3. Numerical Model
3. Proof of Concept: Simulations and Results
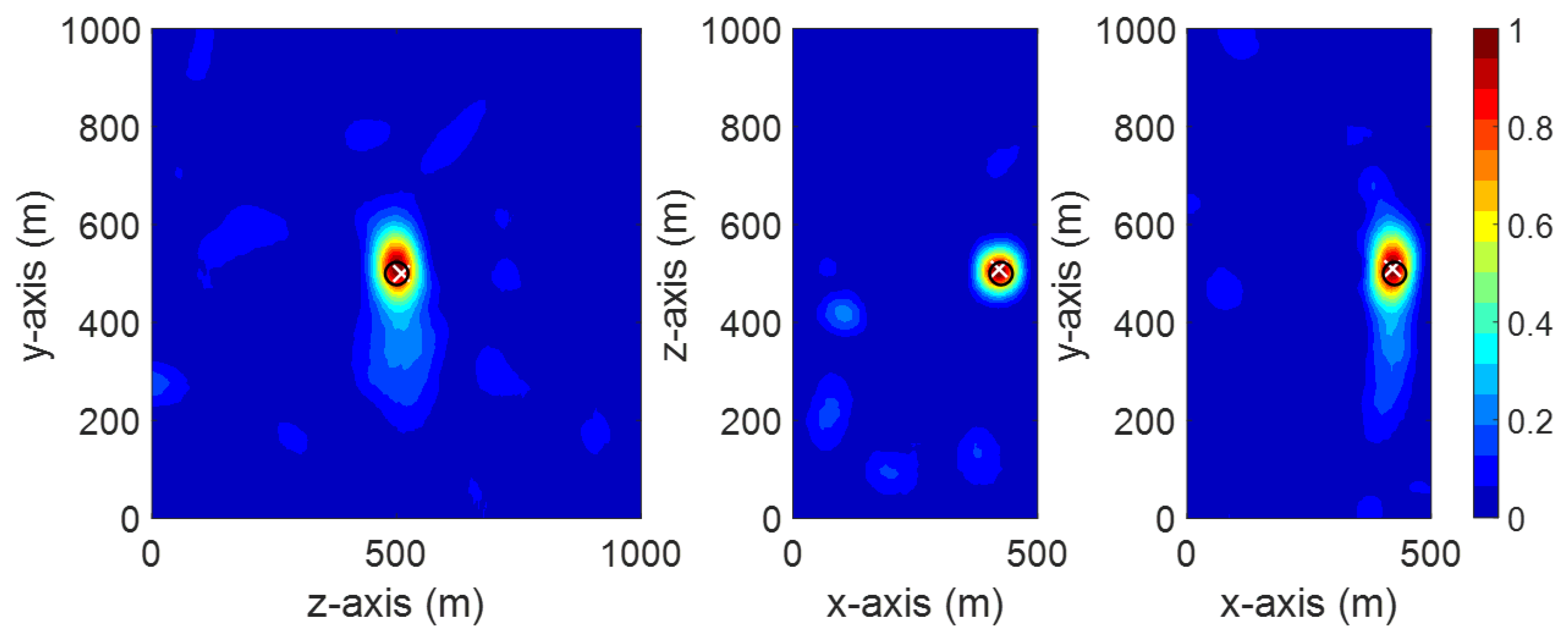
3.1. Capability of the TR Method to Localize a PD Source (CS #1)
3.2. Single Sensor PD Localization (CS #2)
3.3. Single Sensor PD Localization in the Presence of the Active Parts (CS #3)
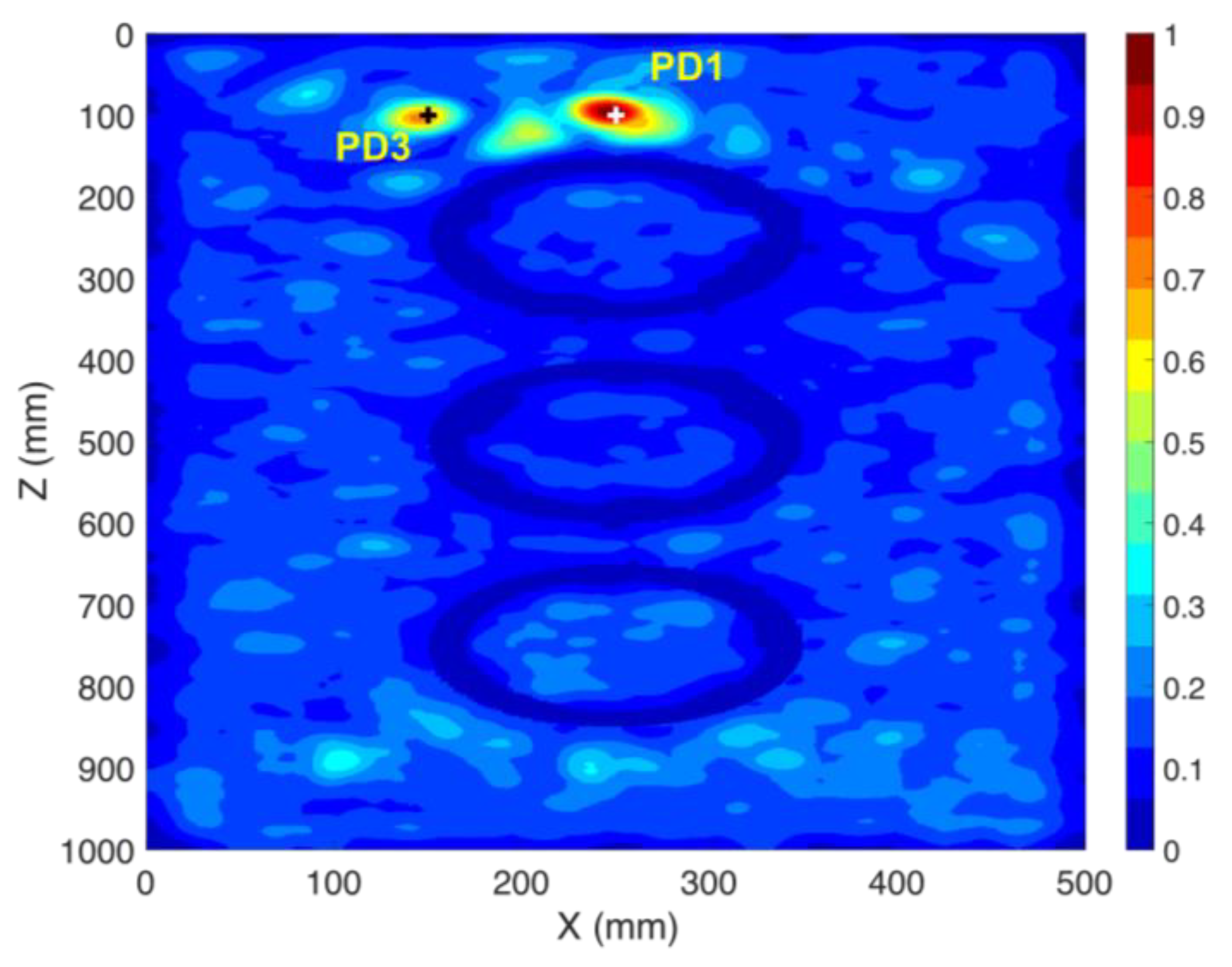
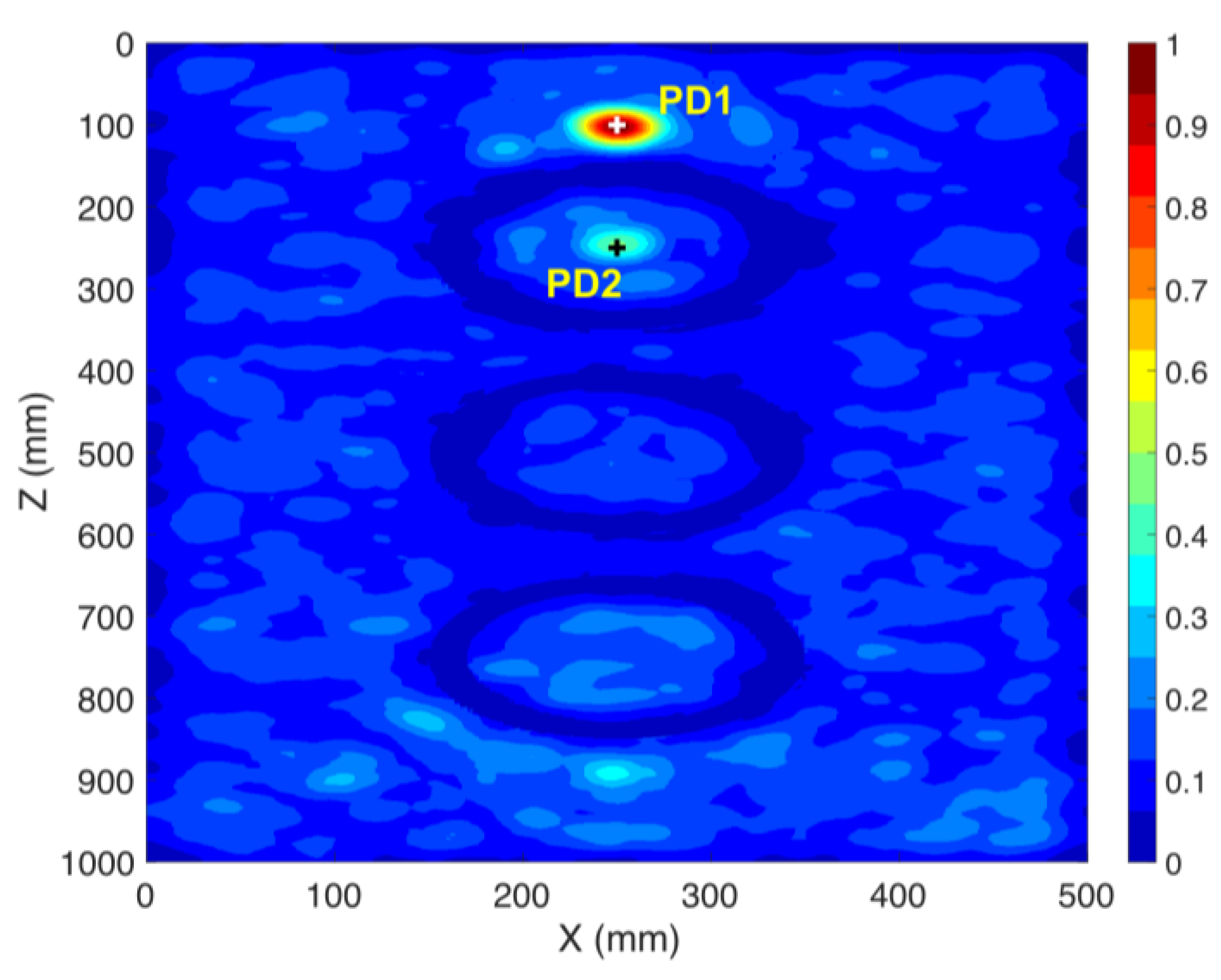
3.4. Localization of Multiple PD Sources using the TR Method (CS #4-5)
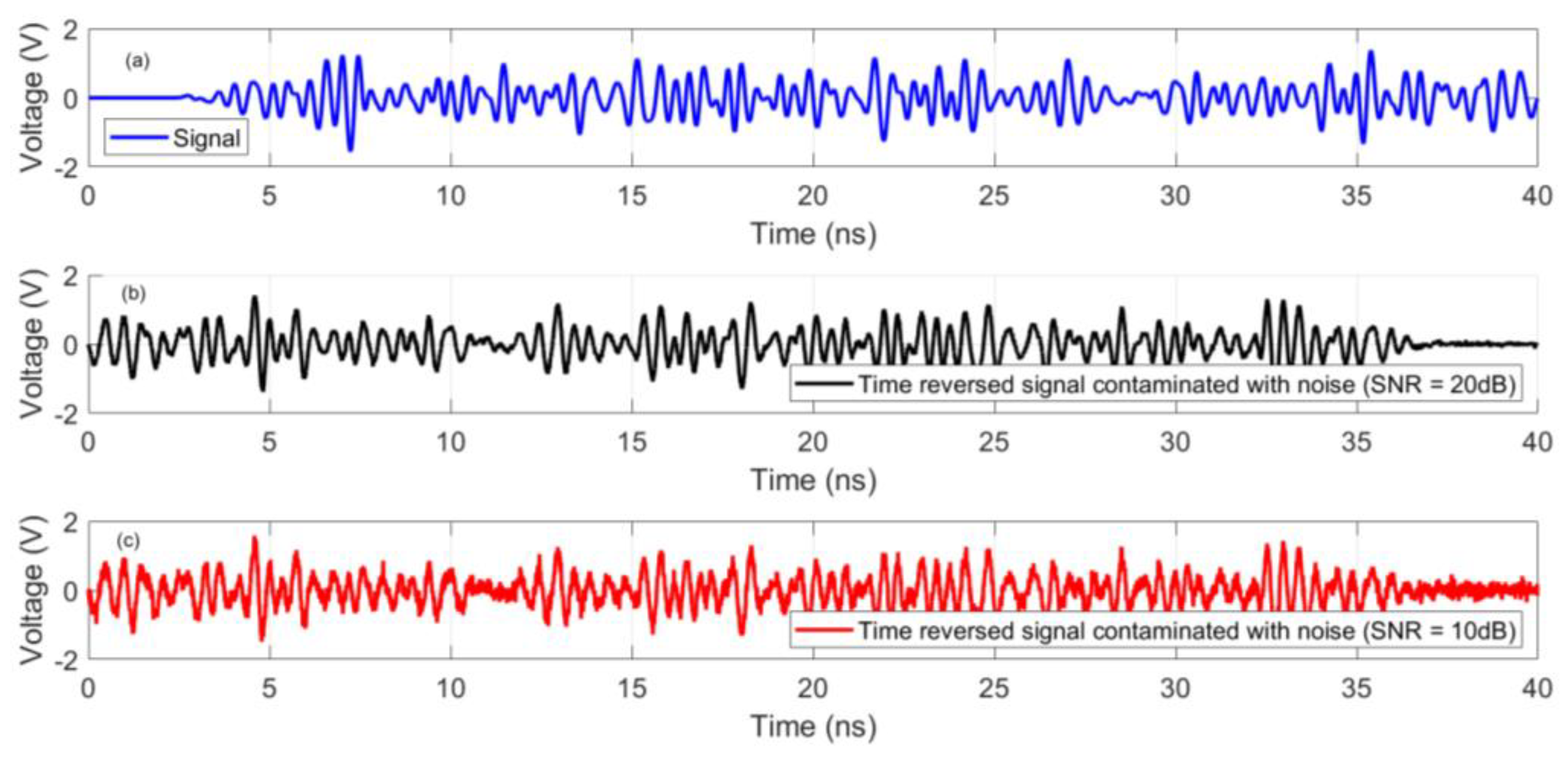
3.5. Further Discussion on the Performance of the Method
3.6. PD Localization in the Presence of the Transformer Core and Windings
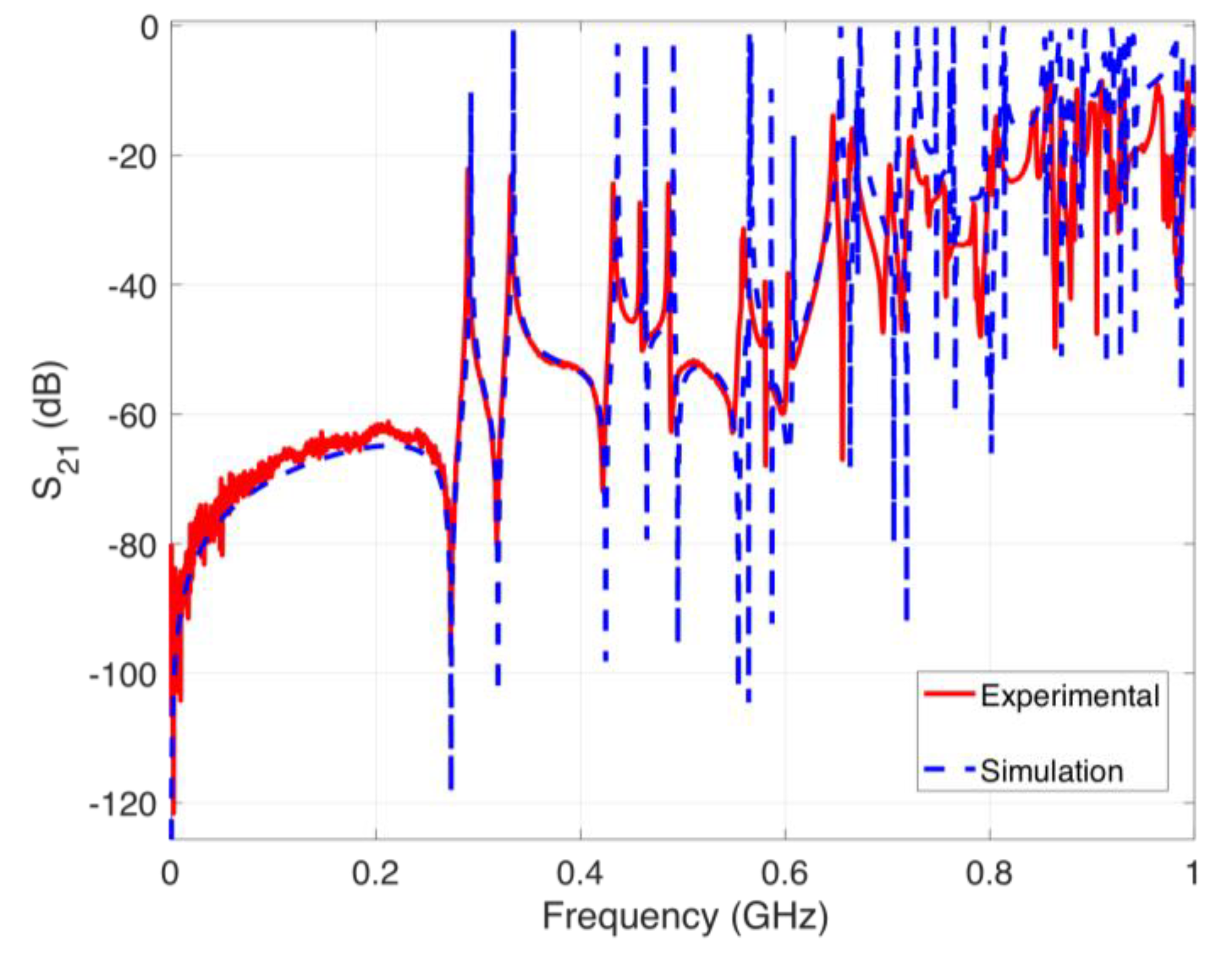
3.7. Verification of the Simulation Scheme
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- W.G D1. 29 CIGRE, Partial Discharges in Transformers. 2017. Available online: http://e-cigre.org/publication/676-partial-discharges-in-transformers (accessed on 3 March 2020).
- Ali, N.H.N.; Giannakou, M.; Nimmo, R.D.; Lewin, P.L.; Rapisarda, P. Classification and localisation of multiple partial discharge sources within a high voltage transformer winding. In Proceedings of the 2016 IEEE Electrical Insulation Conference (EIC), Montereal, QC, Canada, 19–22 June 2016; pp. 519–522. [Google Scholar]
- Hettiwatte, S.N.; Wang, Z.D.; Crossley, P.A.; Darwin, A.; Edwards, G. Experimental investigation into the propagation of partial discharge pulses in transformers. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting, Conference Proceedings (Cat. No. 02CH37309), New York, NY, USA, 27–31 January 2002; pp. 1372–1377. [Google Scholar]
- Duval, M. A review of faults detectable by gas-in-oil analysis in transformers. IEEE Electr. Insul. Mag. 2002, 18, 8–17. [Google Scholar] [CrossRef] [Green Version]
- Markalous, S.M.; Tenbohlen, S.; Feser, K. Detection and location of partial discharges in power transformers using acoustic and electromagnetic signals. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1576–1583. [Google Scholar] [CrossRef]
- Lundgaard, L.E.; Berg, G.; Brede, A.P.; Kyrkjeeide, S.L. Acoustic Location of Discharges in Power Transformers. In Proceedings of the XIIIth International Symposium on High Voltage Engineering, Delft, Netherlands, 25–29 August 2003; pp. 582–583. [Google Scholar]
- Tenbohlen, S.; Pfeffer, A.; Coenen, S. On-site experiences with multi-terminal IEC PD measurements, UHF PD measurements and acoustic PD localisation. In Proceedings of the 2010 IEEE International Symposium on Electrical Insulation, San Diego, CA, USA, 6–9 June 2010; pp. 1–5. [Google Scholar]
- Lundgaard, L.E. Partial discharge. XIV. Acoustic partial discharge detection-practical application. IEEE Electr. Insul. Mag. 1992, 8, 34–43. [Google Scholar] [CrossRef]
- Raja, K.; Floribert, T. Comparative investigations on UHF and acoustic PD detection sensitivity in transformers. In Proceedings of the Conference Record of the the 2002 IEEE International Symposium on Electrical Insulation (Cat. No. 02CH37316), Boston, MA, USA, 7–10 April 2002; pp. 150–153. [Google Scholar]
- Judd, M.D.; Yang, L.; Hunter, I.B.B. Partial discharge monitoring of power transformers using UHF sensors. Part I: Sensors and signal interpretation. IEEE Electr. Insul. Mag. 2005, 21, 5–14. [Google Scholar] [CrossRef]
- Tenbohlen, S.; Denissov, D.; Hoek, S.M.; Markalous, S.M. Partial discharge measurement in the ultra high frequency (UHF) range. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1544–1552. [Google Scholar] [CrossRef]
- Ghorat, M.; Gharehpetian, G.B.; Latifi, H.; Hejazi, M.A. A new partial discharge signal denoising algorithm based on adaptive dual-tree complex wavelet transform. IEEE Trans. Instrum. Meas. 2018, 67, 2262–2272. [Google Scholar] [CrossRef]
- Rachidi, F.; Rubinstein, M.; Paolone, M. (Eds.) Electromagnetic Time Reversal: Application to Electromagnetic Compatibility and Power Systems; John Wiley & Sons Ltd.: Chichester, UK, 2017. [Google Scholar]
- Derode, A.; Tourin, A.; de Rosny, J.; Tanter, M.; Yon, S.; Fink, M. Taking advantage of multiple scattering to communicate with time-reversal antennas. Phys. Rev. Lett. 2003, 90, 014301-1. [Google Scholar] [CrossRef] [PubMed]
- Lerosey, G.; de Rosny, J.; Tourin, A.; Derode, A.; Montaldo, G.; Fink, M. Time Reversal of Electromagnetic Waves. Phys. Rev. Lett. 2004, 92, 193904. [Google Scholar] [CrossRef] [PubMed]
- Carminati, R.; Pierrat, R.; de Rosny, J.; Fink, M. Theory of the time reversal cavity for electromagnetic fields. Opt. Lett. 2007, 32, 3107. [Google Scholar] [CrossRef] [PubMed]
- Karami, H.; Azadifar, M.; Mostajabi, A.; Rubinstein, M.; Rachidi, F. Localization of Electromagnetic Interference Source Using a Time Reversal Cavity: Application of the Maximum Power Criterion. In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility, Signal Integrity and Power Integrity, Reno, NV, USA, 1 January 2020. [Google Scholar]
- Karami, H.; Mostajabi, A.; Azadifar, M.; Wang, Z.; Rubinstein, M.; Rachidi, F. Locating Lightning Using Electromagnetic Time Reversal: Application of the Minimum Entropy Criterion. In Proceedings of the 2019 International Symposium on Lightning Protection (XV SIPDA), São Paulo, Brazil, 30 September–4 October 2019; pp. 1–4. [Google Scholar]
- Karami, H.; Azadifar, M.; Mostajabi, A.; Rubinstein, M.; Rachidi, F. Numerical and Experimental Validation of Electromagnetic Time Reversal for Geolocation of Lightning Strikes. IEEE Trans. Electromagn. Compat. 2019. [Google Scholar] [CrossRef]
- Harrington, R.F. Time-harmonic Electromagnetic Fields; IEEE Press: New York, NY, USA, 2001. [Google Scholar]
- 3D Design; Engineering Software - Dassault Systèmes®. Available online: https://www.3ds.com/products-services/simulia/products/cst-studio-suite/ (accessed on 3 March 2020).
- Karami, H.; Azadifar, M.; Mostajabi, A.; Favrat, P.; Rubinstein, M.; Rachidi, F. Localization of Electromagnetic Interference Sources Using a Time Reversal Cavity. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]







| Case Studies | PD Source(s) | Sensors | Active Parts Incl. (Y/N) | Location Error (mm) |
|---|---|---|---|---|
| CS #1 | PD1 | S1, S2 | N | 6 |
| CS #2 | PD1 | S1 | N | 5 |
| CS #3 | PD1 | S1 | Y | 4 |
| CS #4 | PD1 | S1 | Y | 6 (for PD1) |
| PD3 | 5 (for PD3) | |||
| CS #5 | PD1 | S1 | Y | 3 (for PD1) |
| PD2 | 4 (for PD2) |
| Port | Location [x, y, z] |
|---|---|
| PD1 | [250, 250, 100] |
| PD2 | [250, 250, 250] |
| PD3 | [150, 250, 100] |
| S1 | [100, 50, 900] |
| S2 | [350, 0, 900] |
| Port | Location [x, y, z] |
|---|---|
| PD4 | [425, 500, 500] |
| S3 | [200,100, 950] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karami, H.; Azadifar, M.; Mostajabi, A.; Rubinstein, M.; Karami, H.; Gharehpetian, G.B.; Rachidi, F. Partial Discharge Localization Using Time Reversal: Application to Power Transformers. Sensors 2020, 20, 1419. https://doi.org/10.3390/s20051419
Karami H, Azadifar M, Mostajabi A, Rubinstein M, Karami H, Gharehpetian GB, Rachidi F. Partial Discharge Localization Using Time Reversal: Application to Power Transformers. Sensors. 2020; 20(5):1419. https://doi.org/10.3390/s20051419
Chicago/Turabian StyleKarami, Hamidreza, Mohammad Azadifar, Amirhossein Mostajabi, Marcos Rubinstein, Hossein Karami, Gevork B. Gharehpetian, and Farhad Rachidi. 2020. "Partial Discharge Localization Using Time Reversal: Application to Power Transformers" Sensors 20, no. 5: 1419. https://doi.org/10.3390/s20051419
APA StyleKarami, H., Azadifar, M., Mostajabi, A., Rubinstein, M., Karami, H., Gharehpetian, G. B., & Rachidi, F. (2020). Partial Discharge Localization Using Time Reversal: Application to Power Transformers. Sensors, 20(5), 1419. https://doi.org/10.3390/s20051419







