Radiation Angle Estimation and High-Precision Pedestrian Positioning by Tracking Change of Channel State Information †
Abstract
:1. Introduction
2. Related Research
2.1. Indoor Positioning via Radio Waves
2.2. Estimation of Signal Propagation Distance
2.3. Estimation of Angle of Arrival
2.4. Base Positioning Method
3. Proposed Method
3.1. Overview
3.2. Prerequisites
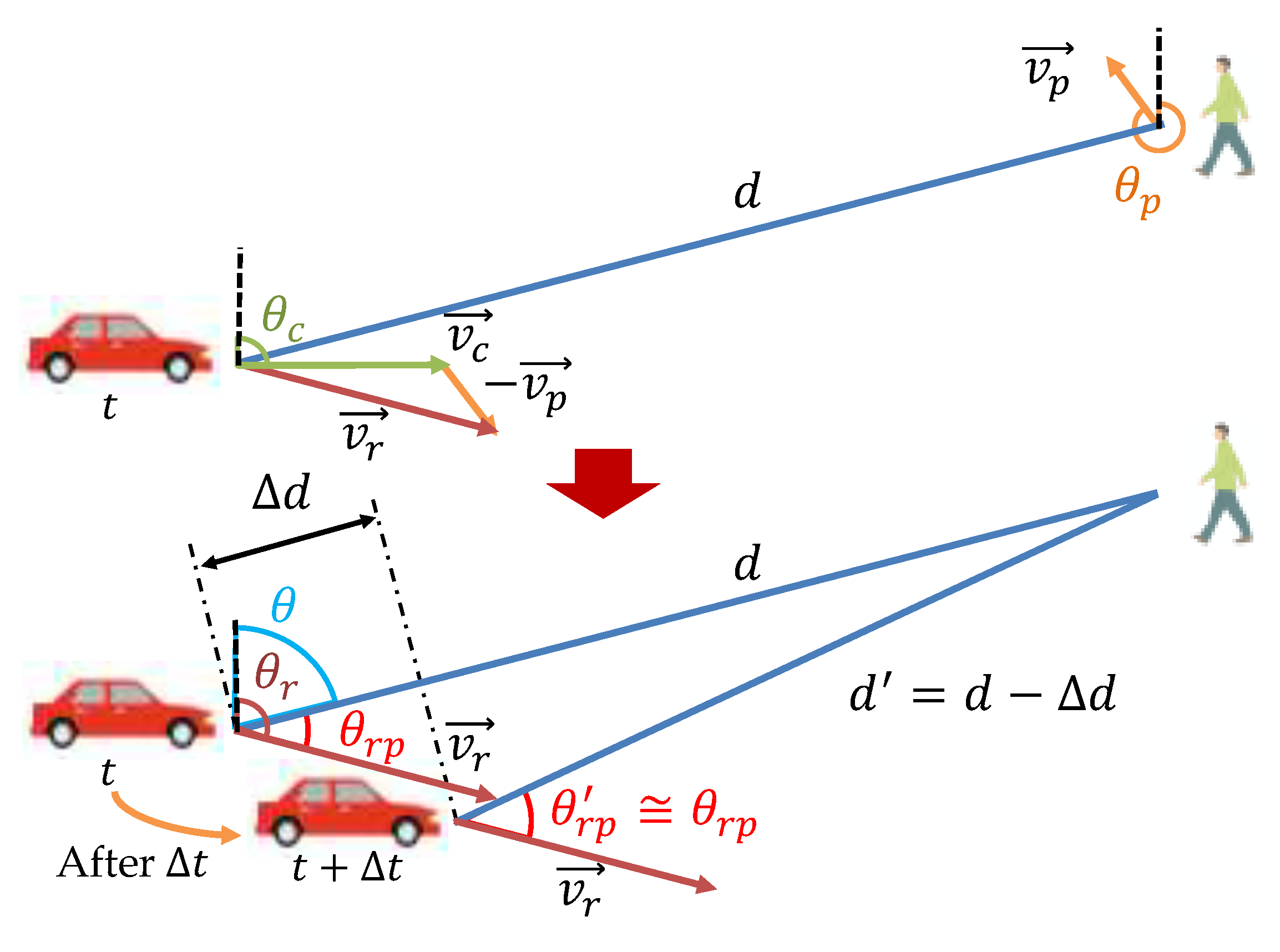
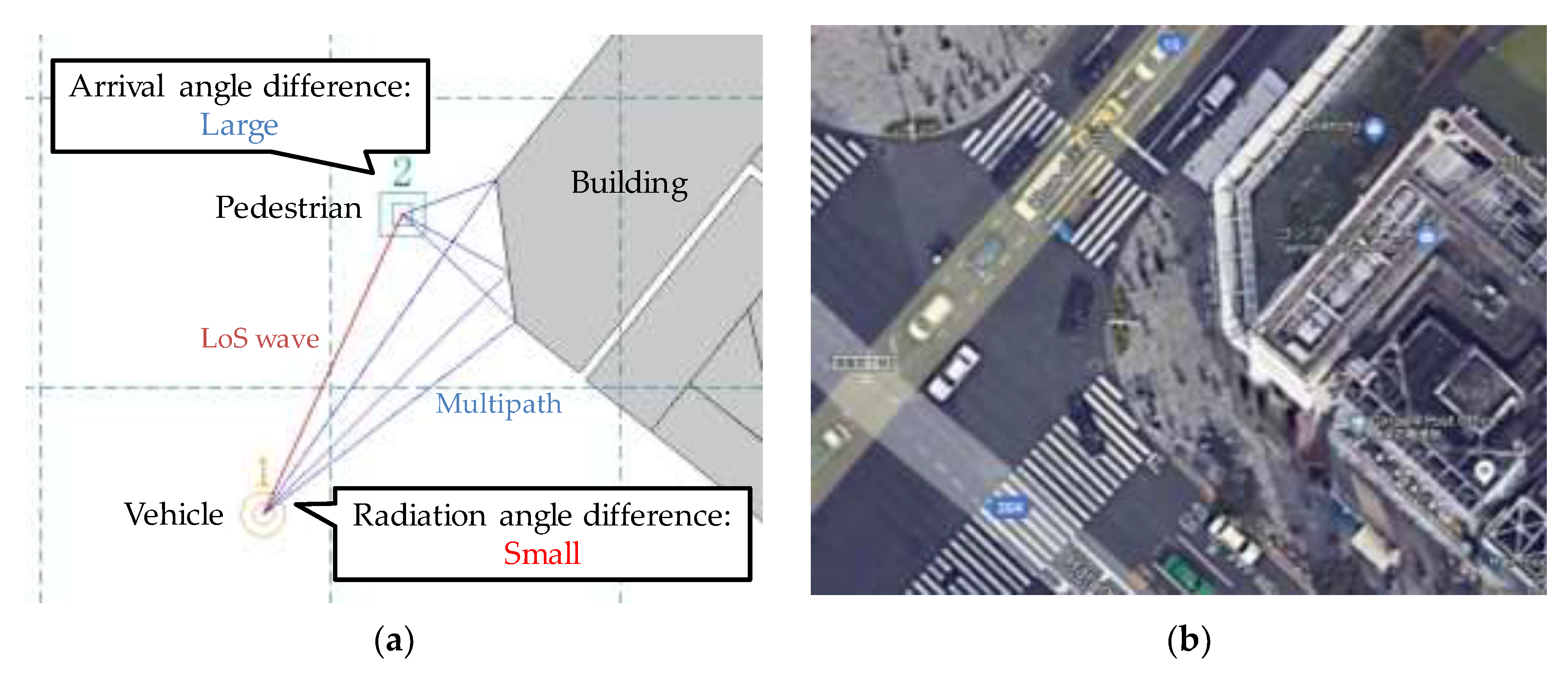
3.3. Estimation of Pedestrian–Vehicle Angle
3.3.1. Phase change due to pedestrian–vehicle movement
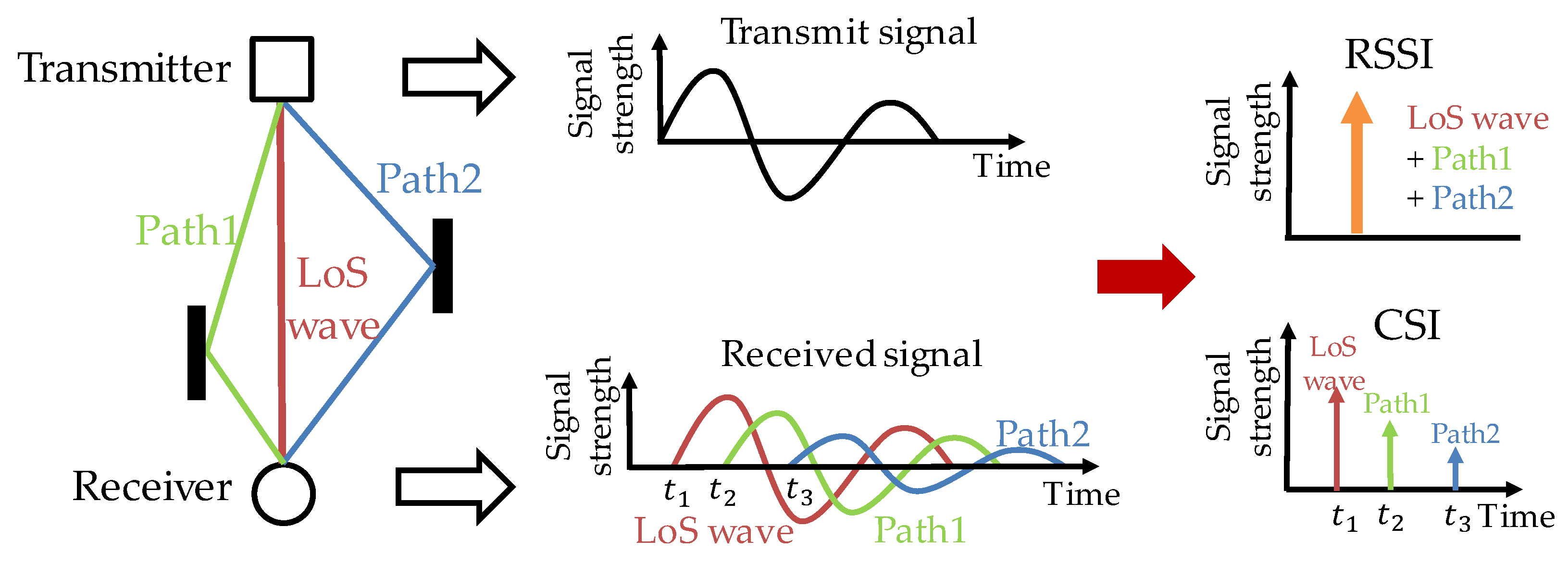
3.3.2. CSI Acquisition
3.3.3. Calculation of the Signal Radiation Angle
3.3.4. Comparison with Previous Methods
3.4. Estimation of Pedestrian–Vehicle Distance
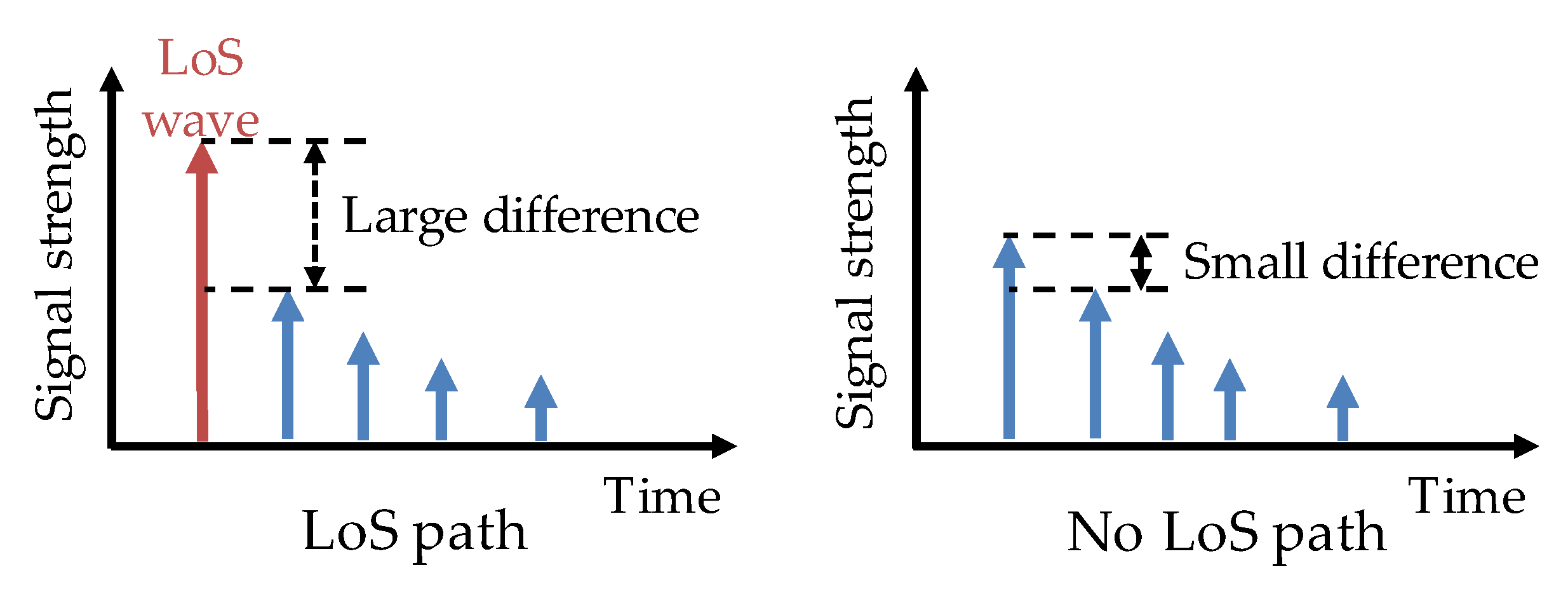
3.5. Presence Detection of the LoS Wave
3.6. Positioning Calculation
3.6.1. Initial Setting
3.6.2. Prediction Step
3.6.3. Update Step
4. Simulation Evaluation
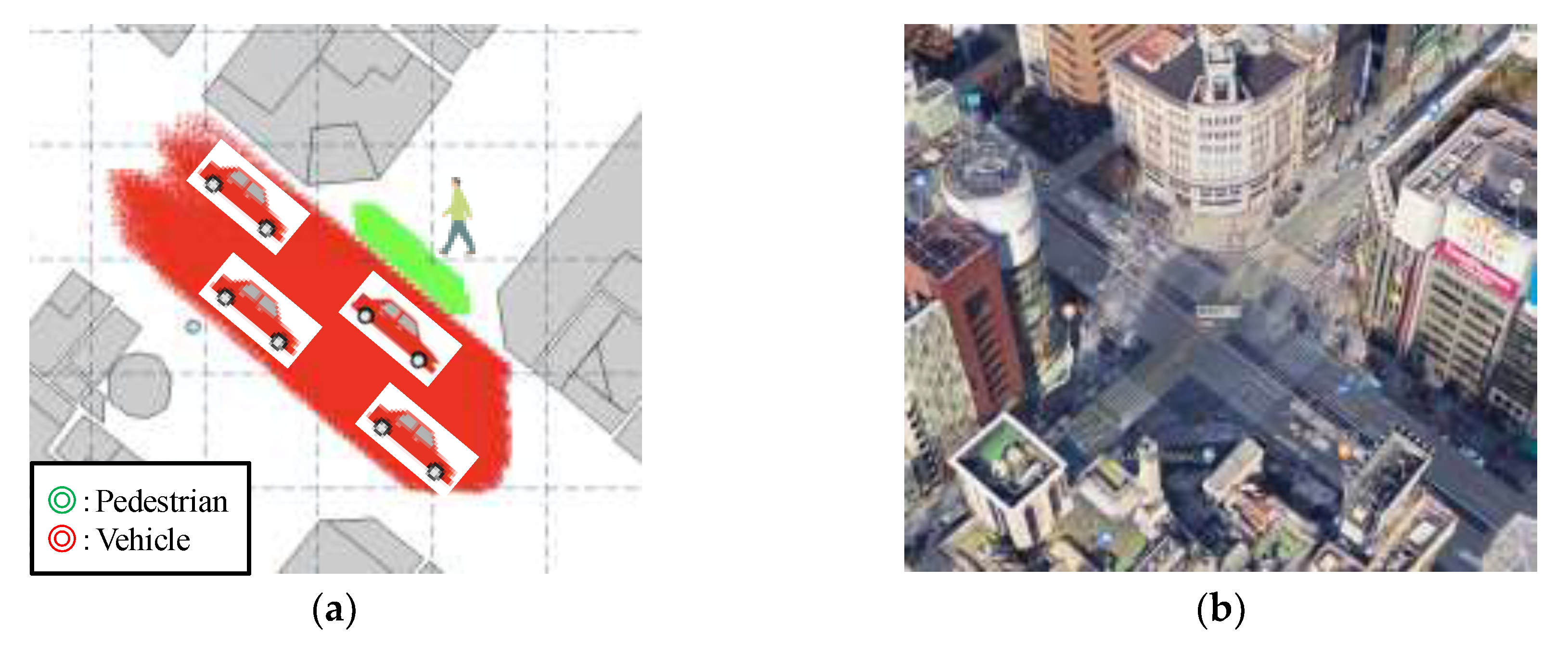
4.1. Simulation Conditions
4.2. Emulation of Time Resolution
4.3. Simulation of Thermal Noise on Signal Propagation Path
4.4. CSI Acquisition Settings
5. Simulation Results and Discussion
5.1. Results for Angle Estimation
5.1.1. Comparison with the base method
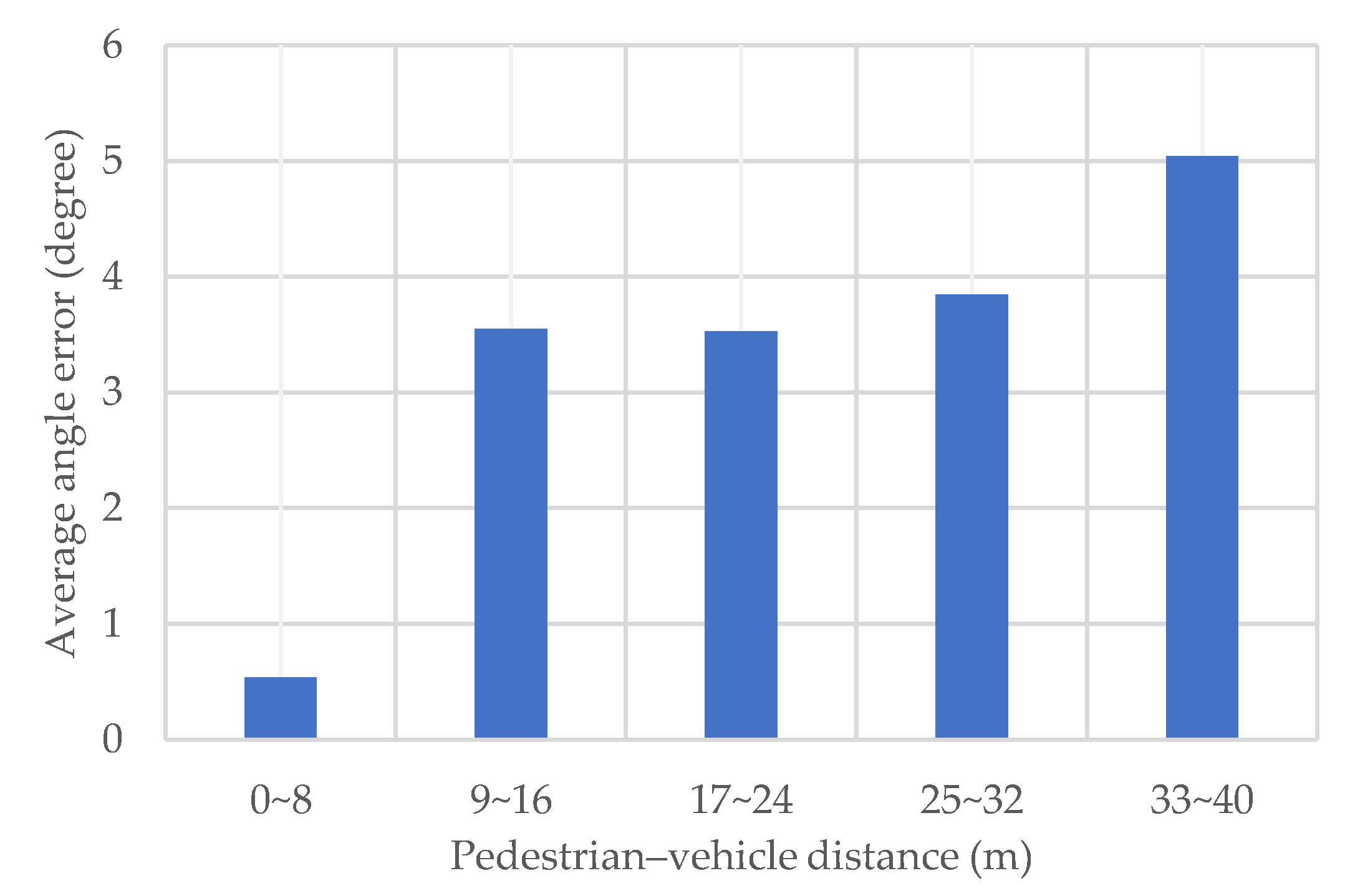
5.1.2. Influence of Pedestrian–Vehicle Distance
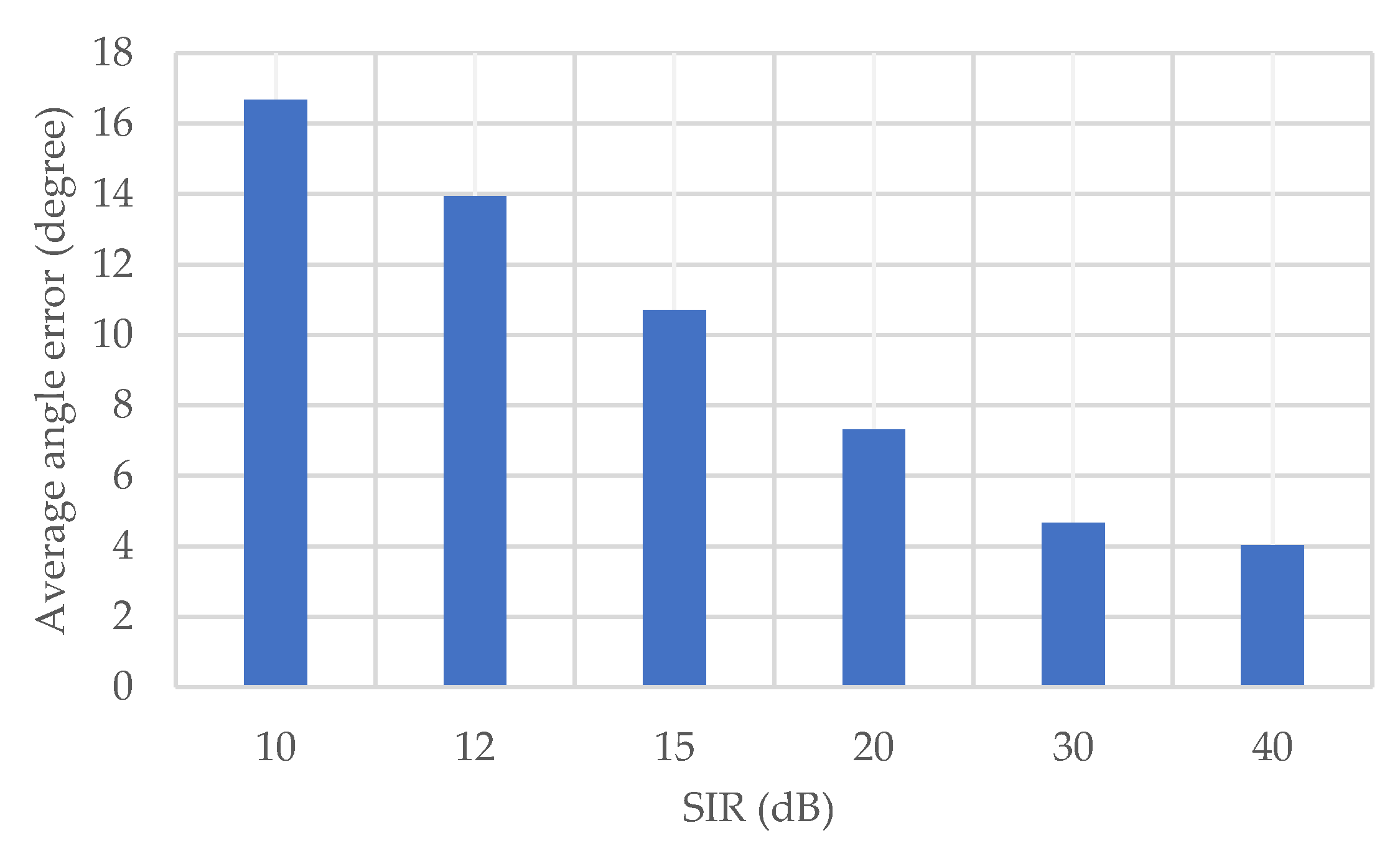
5.1.3. Influence of Interference Wave
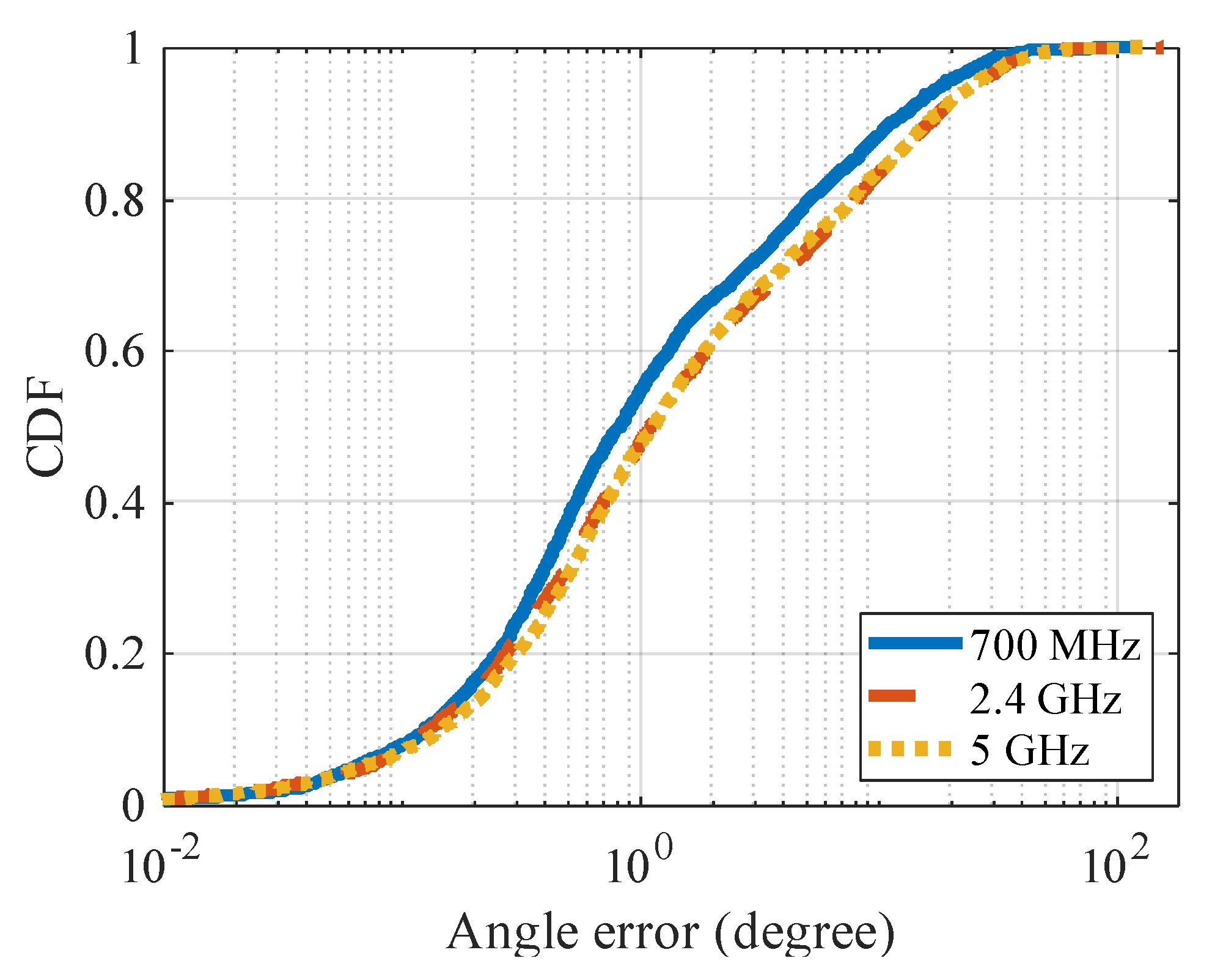
5.1.4. Influence of Signal Transmission Frequency
5.2. Results for Positioning
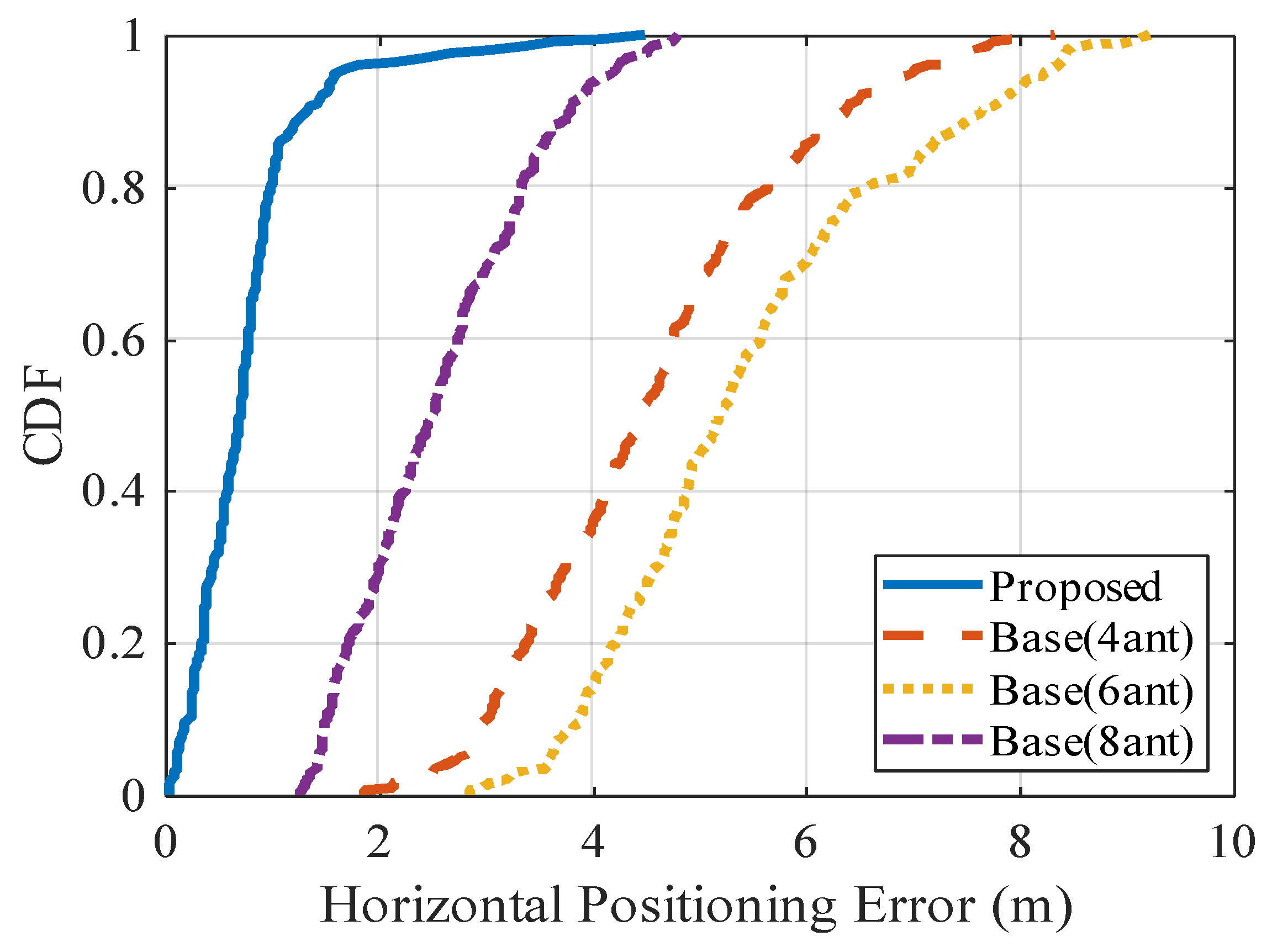
5.2.1. Comparison with the Base Method
5.2.2. Influence of the Number of Vehicles
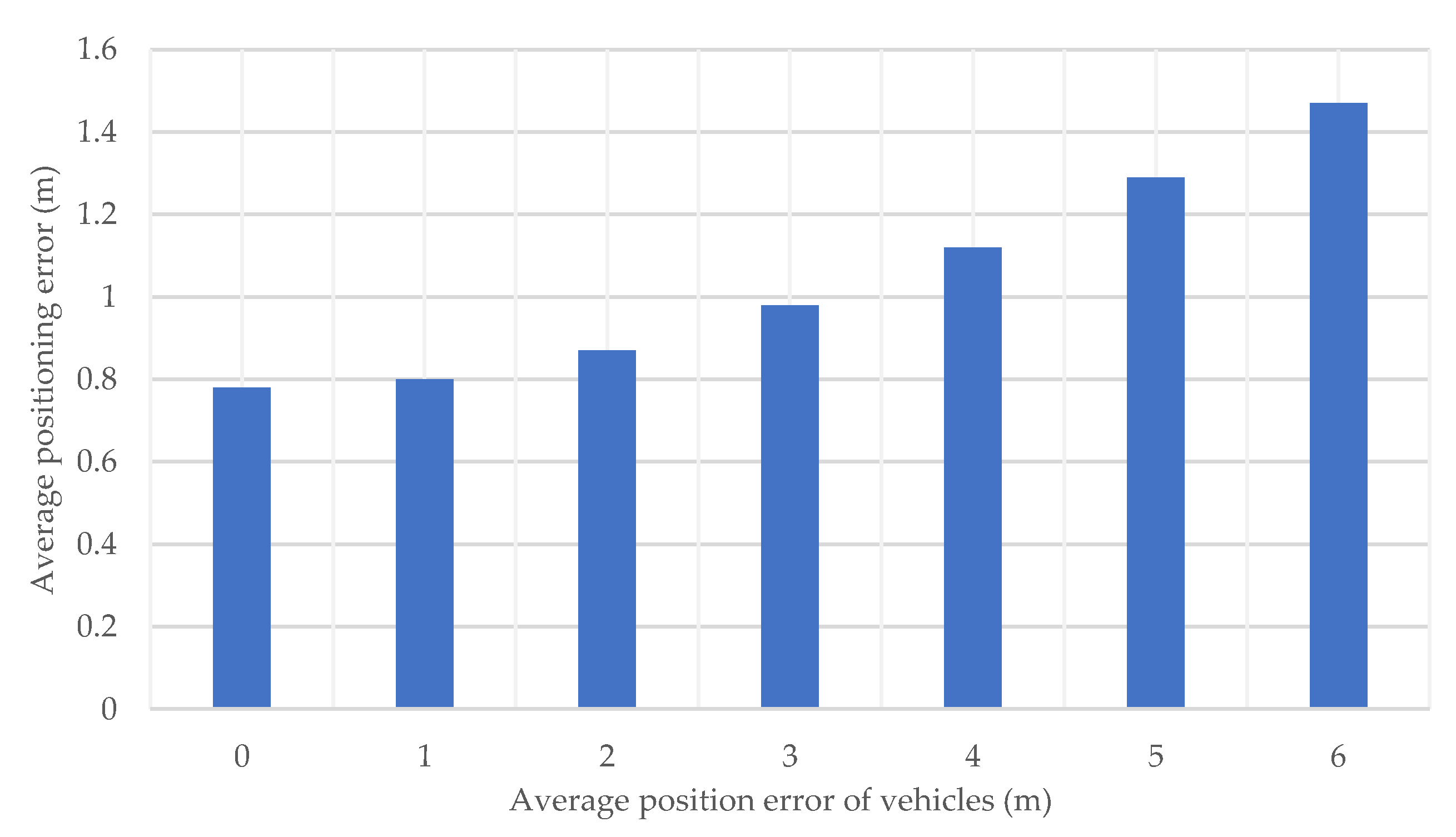
5.2.3. Influence of Position Error of Vehicles
5.2.4. Influence of Interference Wave
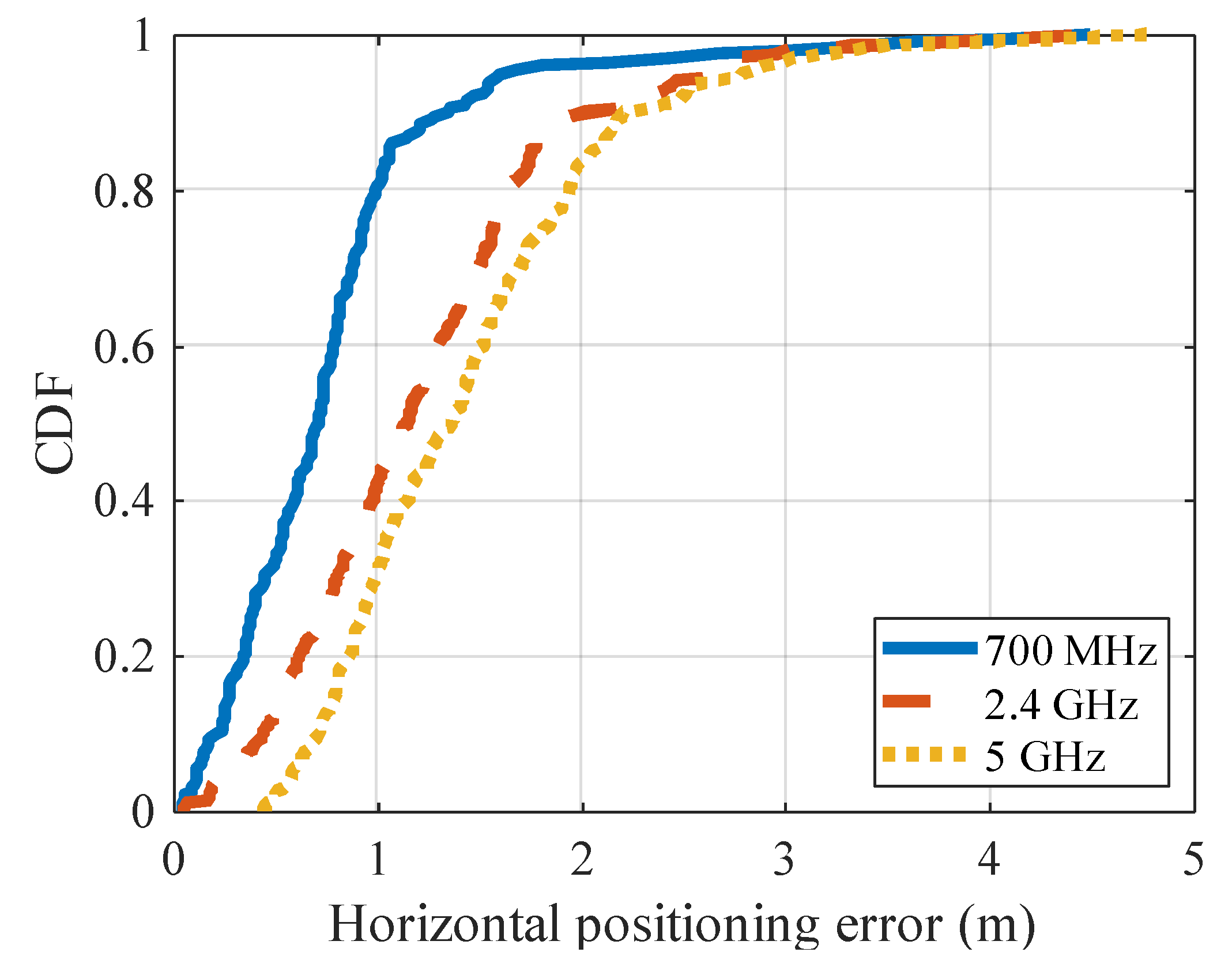
5.2.5. Influence of Signal Transmission Frequency
5.3. Summary
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- ITS Connect Promotion Consortium, Inter-vehicle Communication Message Specifications ITS Connect TD-001 ver. 1.0. 2015. Available online: https://www.itsconnect-pc.org/en/_img/about/TD-001.pdf (accessed on 5 March 2020).
- UTMS Society of Japan, DSSS [Driving Safety Support Systems]. 2020. Available online: http://www.utms.or.jp/english/system/dsss.html (accessed on 4 January 2020).
- TOYOTA, ITS Connect. 2019. Available online: https://toyota.jp/technology/safety/itsconnect/ (accessed on 4 January 2020).
- Tang, S.; Saito, K.; Obana, S. Transmission control for reliable pedestrian-to-vehicle communication by using context of pedestrians. In Proceedings of the 2015 IEEE International Conference on Vehicular Electronics and Safety (ICVES), Yokohama, Japan, 5–7 November 2015; pp. 41–47. [Google Scholar]
- Patou, Y.; Obana, S.; Tang, S. Improvement of pedestrian positioning precision by using spatial correlation of multipath error. In Proceedings of the 2018 IEEE International Conference on Vehicular Electronics and Safety (ICVES), Madrid, Spain, 12–14 September 2018. [Google Scholar]
- Hsu, L.; Chen, F.; Kamijo, S. Evaluation of Multi- GNSSs and GPS with 3D Map Methods for Pedestrian Positioning in an Urban Canyon Environment. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2015, 98, 284–293. [Google Scholar] [CrossRef]
- Kwon, C.; Hwang, I. Constrained stochastic hybrid system modeling to road map—GPS integration for vehicle positioning. In Proceedings of the 2016 IEEE 55th Conference on Decision and Control (CDC), Las Vegas, NV, USA, 12–14 December 2016. [Google Scholar]
- Youwen, L. Forecast Map Matching Model for Vehicle-borne Navigation Based on Roadway Characteristic. In Proceedings of the 2010 International Conference on Optoelectronics and Image Processing, Haikou, China, 11–12 November 2010; Volume 1, pp. 569–571. [Google Scholar]
- Yamashita, R.; Tang, S.; Obana, S. Proposal and evaluation of pedestrian positioning method by using signals from both GPS satellites and vehicles. IPSJ J. 2018, 59, 113–123. [Google Scholar]
- Tang, S.; Obana, S. Improving performance of pedestrian positioning by using vehicular communication signals. IET Intell. Transp. Syst. 2018. [Google Scholar] [CrossRef] [Green Version]
- Toda, K.; Tang, S.; Obana, S. High-Precision Pedestrian Positioning by Using Radio Signals from Vehicles and Roadside Units. In Proceedings of the 2019 International Conference on Electronics, Information, and Communication, Auckland, New Zealand, 22–25 January 2019. [Google Scholar]
- Komamiya, W.; Obana, S.; Tang, S. Single Antenna Precise Angle Estimation by Exploiting Doppler Shift and its Application in Pedestrian Positioning. In Proceedings of the 2019 IEEE International Conference of Vehicular Electronics and Safety (ICVES), Cairo, Egypt, 4–6 September 2019. [Google Scholar]
- Xie, Y.; Li, Z.; Li, M. Precise power delay profiling with commodity Wi-Fi. IEEE Trans. Mob. Comput. 2018, 18, 1342–1355. [Google Scholar] [CrossRef]
- Vasisht, D.; Kumar, S.; Katabi, D. Decimeter-level localization with a single Wi-Fi access point. In Proceedings of the 13th {USENIX} Symposium on Networked Systems Design and Implementation ({NSDI}, Santa Clara, CA, USA, 16–18 March 2016; pp. 165–178. [Google Scholar]
- Sen, S.; Lee, J.; Kim, K.-H.; Congdon, P. Avoiding multipath to revive inbuilding Wi-Fi localization. In Proceedings of the 11th Annual International Conference on Mobile Systems, Applications, and Services, Taipei, Taiwan, 25–28 June 2013; pp. 249–262. [Google Scholar]
- Wielandt, S.; Strycker, L. Indoor Multipath Assisted Angle of Arrival Localization. Sensors 2017, 17, 2522. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kotaru, M.; Joshi, K.; Bharadia, D.; Katti, S. Spotfi: Decimeter level localization using Wi-Fi. In Proceedings of the 2015 ACM Conference on Special Interest Group on Data Communication, London, UK, 17–21 August 2015; pp. 269–282. [Google Scholar]
- Wang, X.; Gao, L.; Mao, S.; Pandey, S. CSI-based fingerprinting for indoor localization: A deep learning approach. IEEE Trans. Veh. Technol. 2017, 66, 763–776. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Xu, Q.; Li, J.; Fu, C.; Xuan, Q.; Xiang, Y. Passive Indoor Localization Based on CSI and Naive Bayes Classification. IEEE Trans. Syst. 2018, 48, 1566–1577. [Google Scholar] [CrossRef]
- Qian, K.; Wu, C.; Yang, Z.; Liu, Y.; He, F.; Xing, T. Enabling Contactless Detection of Moving Humans with Dynamic Speeds Using CSI. ACM Trans. Embed. Comput. Syst. 2018, 17, 1–18. [Google Scholar] [CrossRef]
- Yang, Z.; Zhou, Z.; Liu, Y. From RSSI to CSI: Indoor Localization via Channel Response. ACM Comput. Surv. 2013, 46, 1–32. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef] [Green Version]
- Cidronali, A.; Maddio, S.; Giorgetti, G.; Manes, G. Analysis and Performance of a Smart Antenna for 2.45-GHz Single-Anchor Indoor Positioning. IEEE Trans. Microw. Theory Tech. 2010, 58, 21–31. [Google Scholar] [CrossRef]
- Chang, H.; Tian, J.; Lai, T.; Chu, H.; Huang, P. Spinning Beacons for Precise Indoor Localization. In Proceedings of the 6th ACM Conference on Embedded Network Sensor Systems, Raleigh, NC, USA, 5–7 November 2008; pp. 127–140. [Google Scholar]
- Kozo Keikaku Engineering, RapLab, Radio Wave Propagation Analysis Tool. 2019. Available online: https://www.kke.co.jp/en/solution/theme/raplab.html (accessed on 4 January 2020).







| Simulator | RapLab (3D ray Tracing) MATLAB (Distance/Angle/Position Calculation) |
| Trial conditions | 200 times every 0.1 s from 2019/1/1 PM1:00 |
| Vehicle position/number | 2 lanes on each side, move at 60 km/h, randomly arranged with a head way distance of 5 to 30 m, 15 vehicles on average |
| Pedestrian position | 1 person, moves on the pedestrian crossing (4 km/h) |
| Satellite | GPS satellites (elevation angle 15 degrees or more) |
| Vehicle signal | Center frequency: 700 MHz, Transmit power: 20 dBm, transmit interval: 0.1 s |
| 3D raytracing | Maximum number of signal reflection: 1 Maximum number of signal diffraction: 1 |
| Vehicle position error | None |
| Proposed | Base | |||
|---|---|---|---|---|
| 8 antennas | 6 antennas | 4 antennas | ||
| Angle error | 3.90 | 13.00 | 15.56 | 18.70 |
| 700 MHz | 2.4 GHz | 5 GHz | |
|---|---|---|---|
| Angle error | 3.90 | 5.36 | 5.23 |
| Proposed | Base | |||
|---|---|---|---|---|
| 8 antennas | 6 antennas | 4 antennas | ||
| Positioning error | 0.78 | 2.49 | 5.46 | 4.58 |
| 700 MHz | 2.4 GHz | 5 GHz | |
|---|---|---|---|
| Positioning error | 0.78 | 1.23 | 1.46 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komamiya, W.; Tang, S.; Obana, S. Radiation Angle Estimation and High-Precision Pedestrian Positioning by Tracking Change of Channel State Information. Sensors 2020, 20, 1430. https://doi.org/10.3390/s20051430
Komamiya W, Tang S, Obana S. Radiation Angle Estimation and High-Precision Pedestrian Positioning by Tracking Change of Channel State Information. Sensors. 2020; 20(5):1430. https://doi.org/10.3390/s20051430
Chicago/Turabian StyleKomamiya, Wataru, Suhua Tang, and Sadao Obana. 2020. "Radiation Angle Estimation and High-Precision Pedestrian Positioning by Tracking Change of Channel State Information" Sensors 20, no. 5: 1430. https://doi.org/10.3390/s20051430
APA StyleKomamiya, W., Tang, S., & Obana, S. (2020). Radiation Angle Estimation and High-Precision Pedestrian Positioning by Tracking Change of Channel State Information. Sensors, 20(5), 1430. https://doi.org/10.3390/s20051430





