Expanding Bias-instability of MEMS Silicon Oscillating Accelerometer Utilizing AC Polarization and Self-Compensation
Abstract
1. Introduction
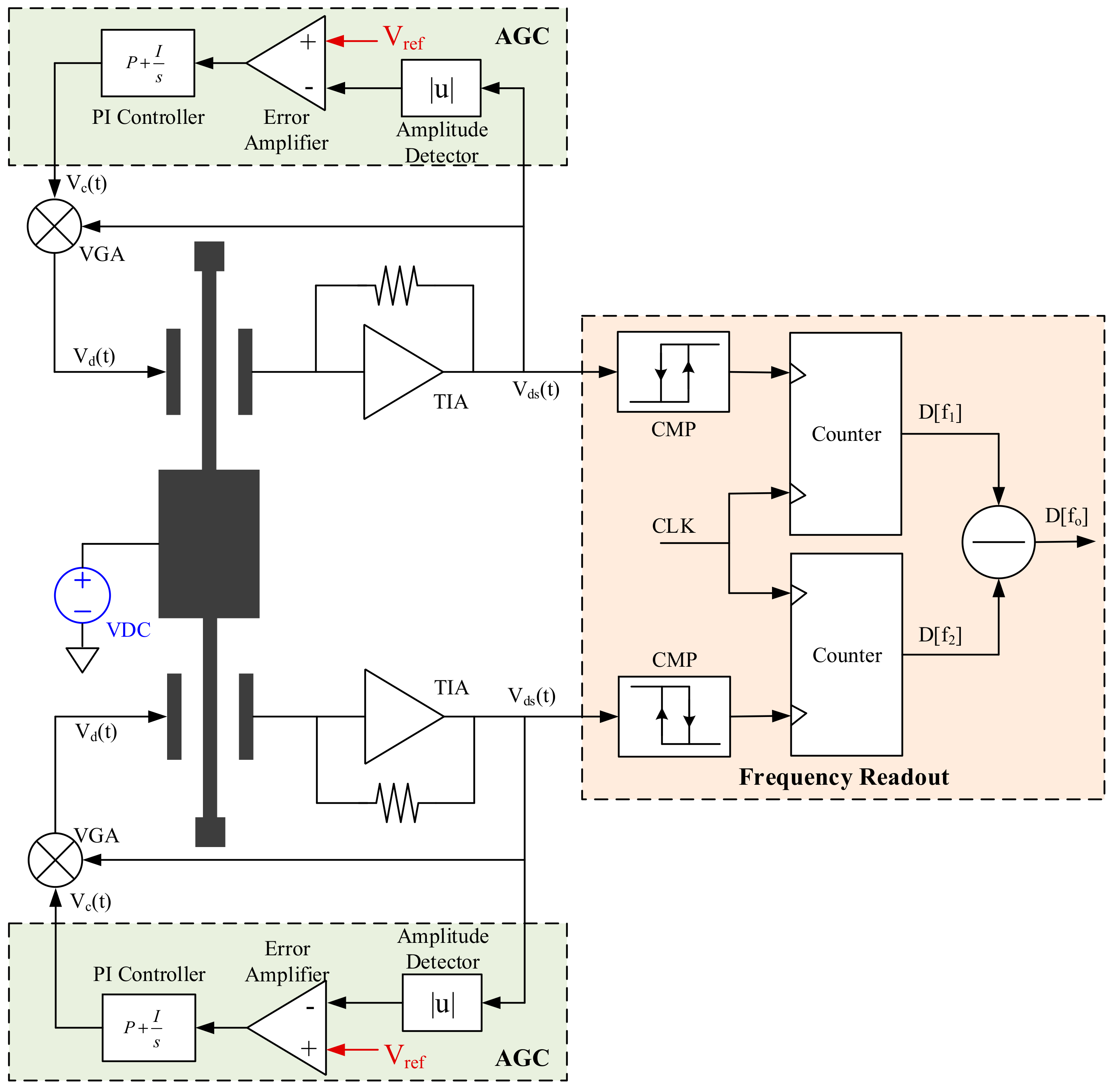
2. MEMS SOA Overview
3. AC Polarization Technique
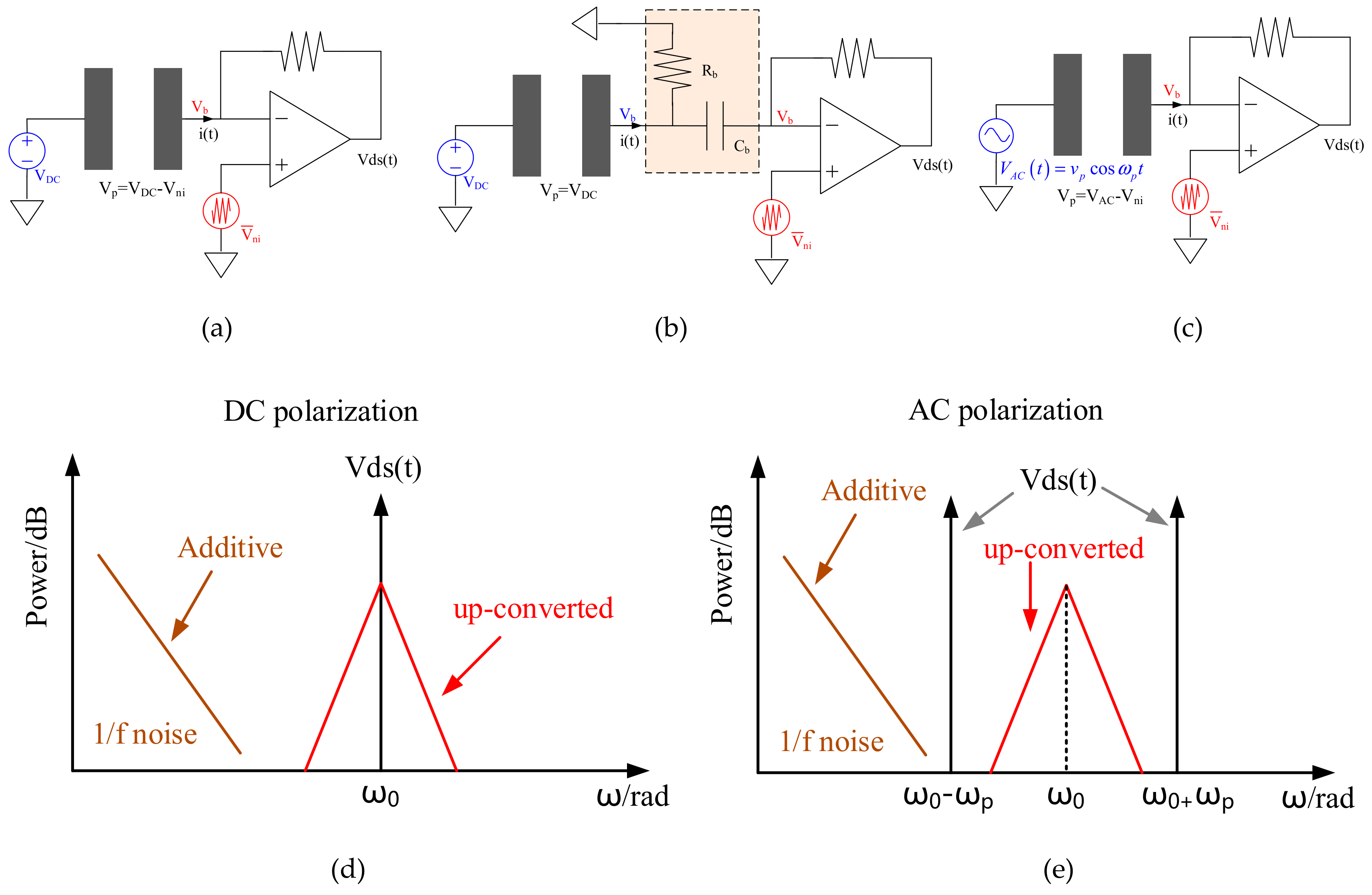
3.1. Why AC Polarization?
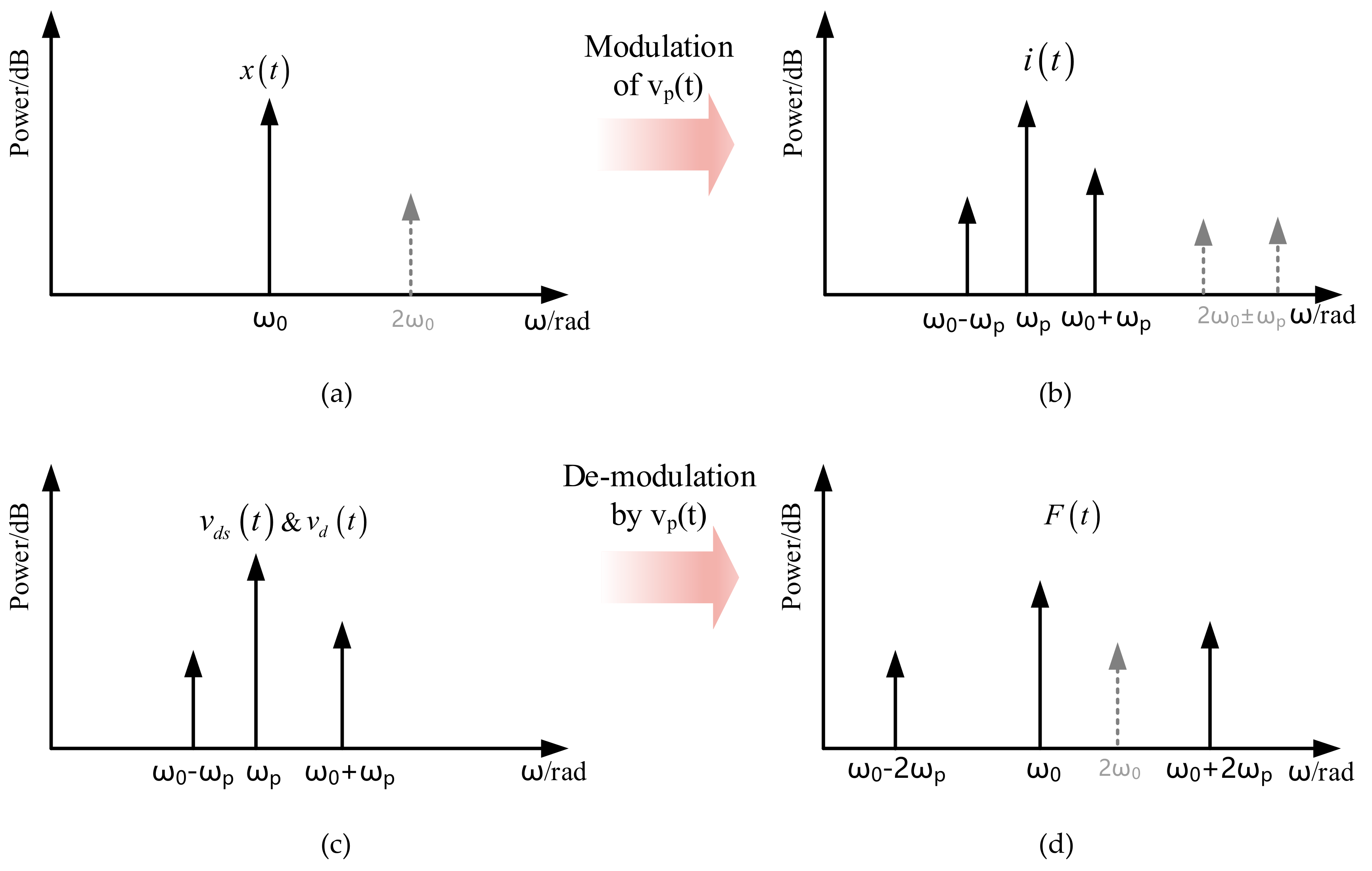
3.2. Fundamentals of AC Polarization
3.3. Closed-Loop Oscillator Measurement
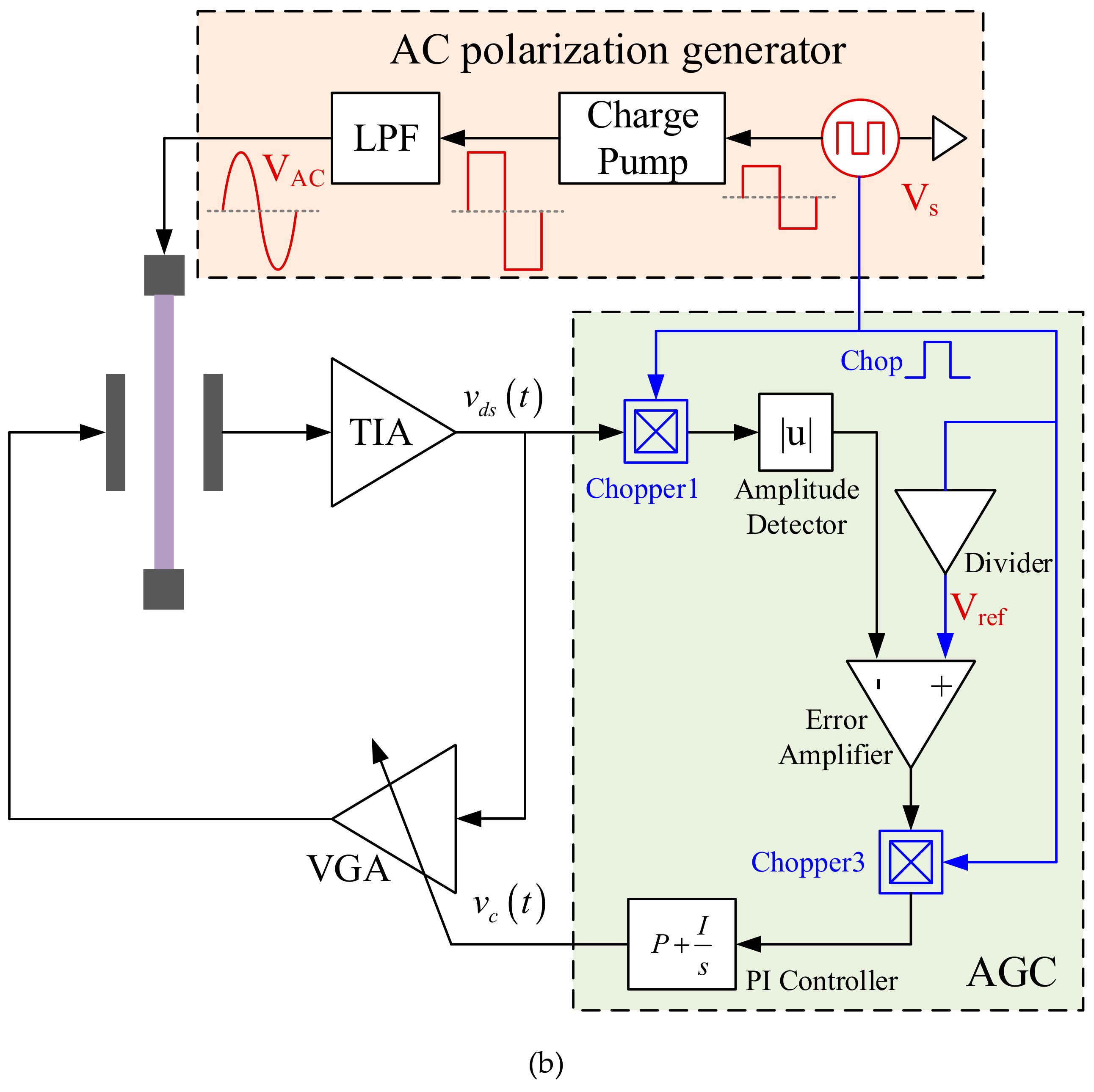
4. Self-Compensation of AC Polarization Source
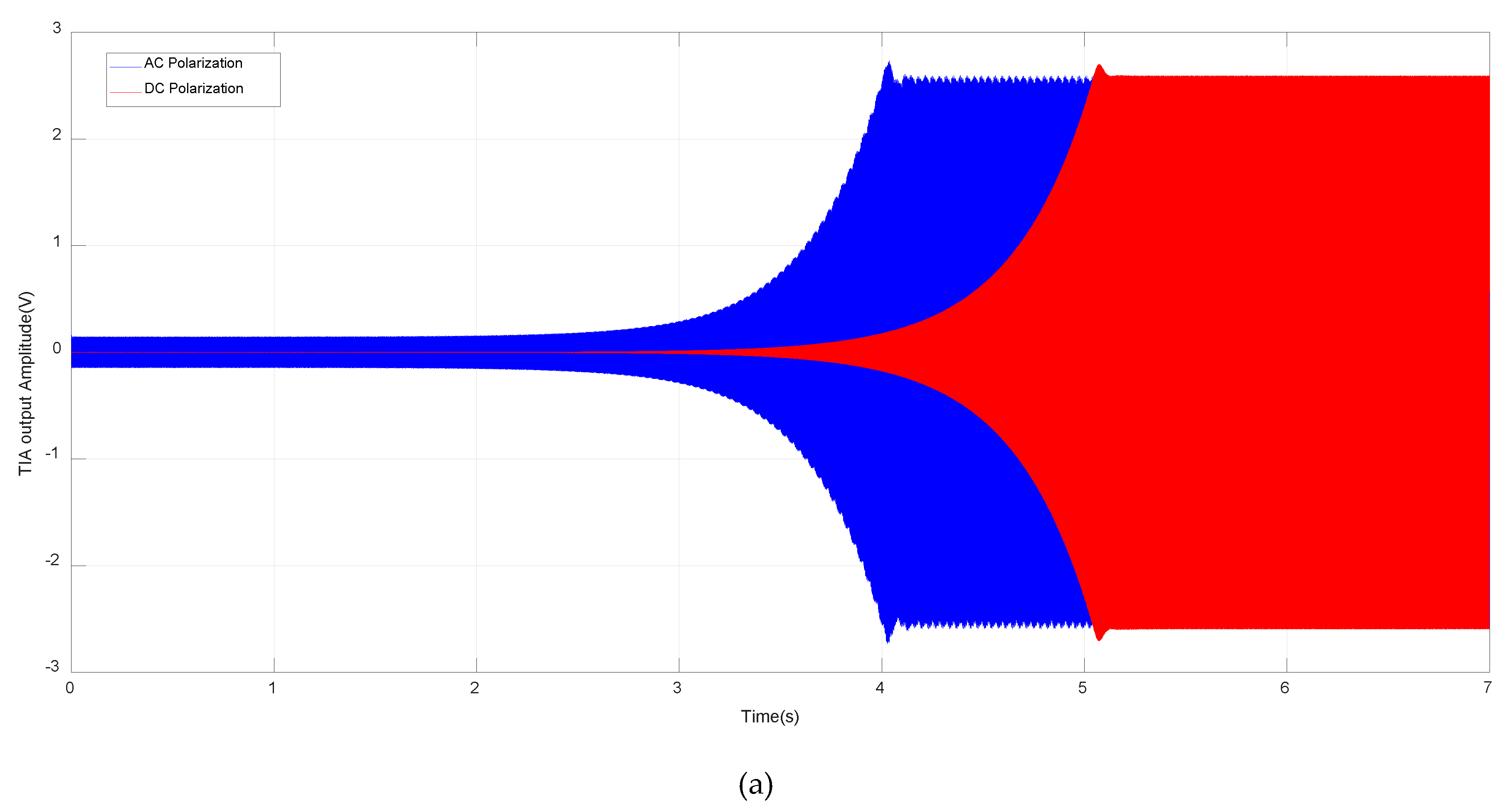
5. SOA Experiment Results
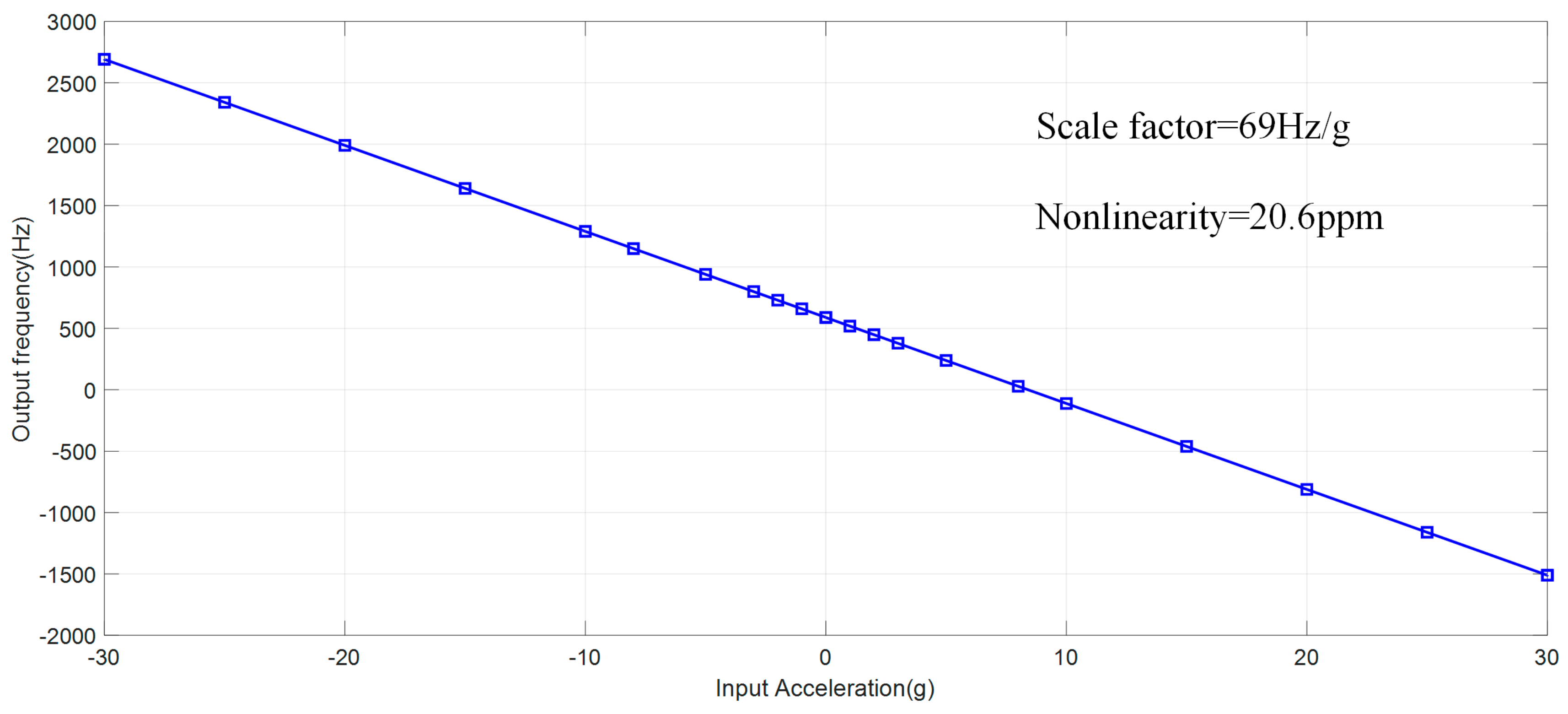
5.1. Acceleration Response
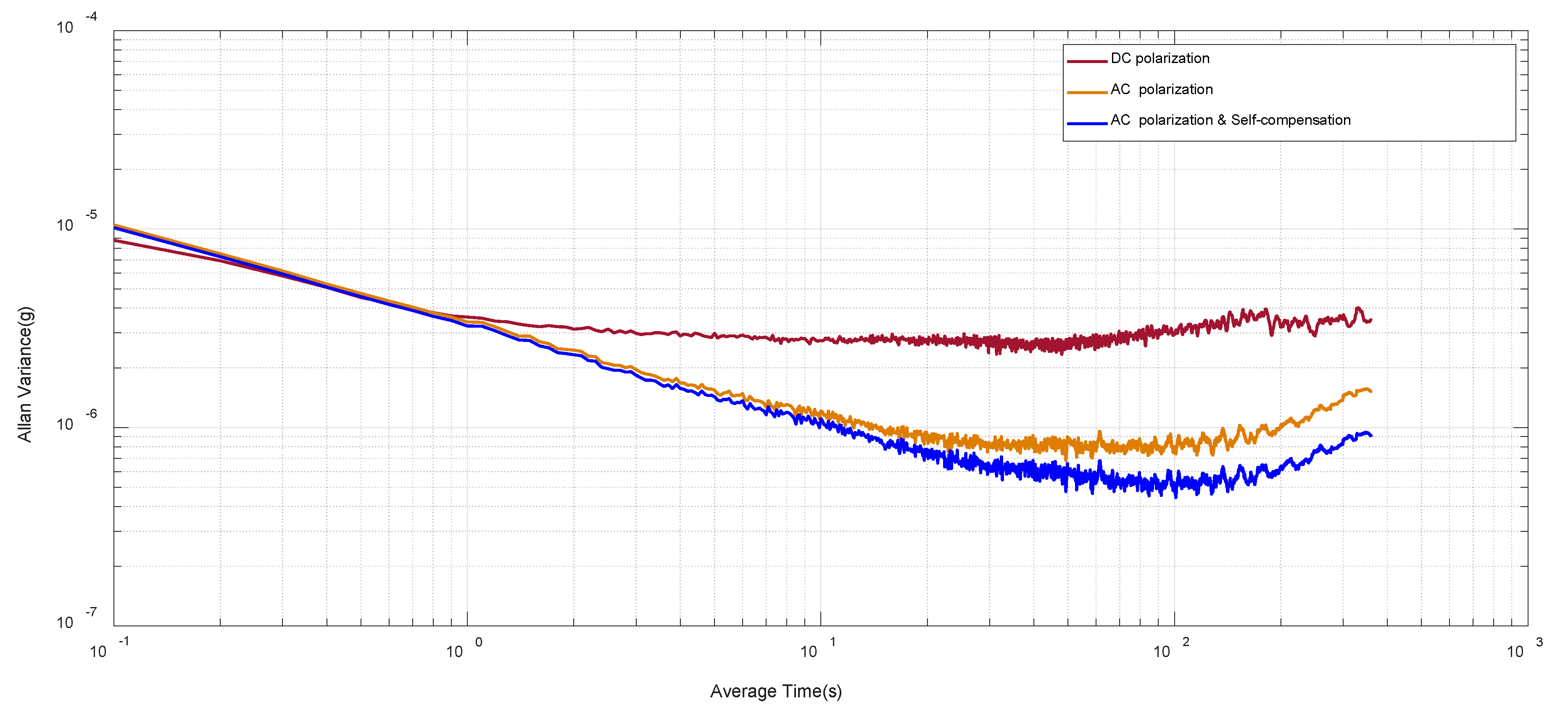
5.2. Allan Variance
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Prikhodko, I.P.; Bearss, B.; Merritt, C.; Bergeron, J.; Blackmer, C. Towards self-navigating cars using MEMS IMU: Challenges and opportunities. In Proceedings of the 2018 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Lake Como, Italy, 26–29 March 2018. [Google Scholar]
- D’Alessandro, A.; D’Anna, R.; Greco, L.; Passafiume, G.; Scudero, S.; Speciale, S.; Vitale, G. Monitoring Earthquake through MEMS Sensors (MEMS project) in the town of Acireale (Italy). In Proceedings of the 2018 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Lake Como, Italy, 26–29 March 2018. [Google Scholar]
- Xie, L.; Tian, J.; Ding, G.; Zhao, Q. Human activity recognition method based on inertial sensor and barometer. In Proceedings of the 2018 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Lake Como, Italy, 26–29 March 2018. [Google Scholar]
- Monica, A.D.; Ruotsalainen, L.; Dovis, F. Multisensor navigation in urban environment. In Proceedings of the 2018 IEEE/ION Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 23–26 April 2018. [Google Scholar]
- Shimoyama, I. MEMS Sensors for Robots. In Proceedings of the 2019 IEEE 32nd International Conference on Micro Electro Mechanical Systems (MEMS), Seoul, Korea, 27–31 January 2019. [Google Scholar]
- Lefort, O.; Thomas, I.; Jaud, S. To the production of a robust and highly accurate MEMS vibrating accelerometer. In Proceedings of the 2017 DGON Inertial Sensors and Systems (ISS), Karlsruhe, Germany, 19–20 September 2017. [Google Scholar]
- Pandit, M.; Mustafazade, A.; Zhao, C.; Sobreviela, G.; Zou, X.; Steinmann, P.; Seshia, A. An Ultra-High Resolution Resonant MEMS Accelerometer. In Proceedings of the 2019 IEEE 32nd International Conference on Micro Electro Mechanical Systems (MEMS), Seoul, Korea, 27–31 January 2019. [Google Scholar]
- Hopkins, R.E.; Borenstein, J.T.; Antkowiak, B.M.; Ward, P.A.; Elliott, R. The Silicon Oscillating Accelerometer: A MEMS Inertial Instrument for Strategic Missile Guidance. In Proceedings of the Missile Sciences Conference, Monterey, CA, USA, 7–9 November 2000. [Google Scholar]
- Seshia, A.; Palaniapan, M.; Roessig, T.A.; Howe, R.T.; Gooch, R.W.; Schimert, T.R.; Montague, S. A vacuum packaged surface micromachined resonant accelerometer. J. Microelectromech. Syst. 2002, 11, 784–793. [Google Scholar] [CrossRef]
- Zou, X.; Thiruvenkatanathan, P.; Seshia, A. A Seismic-Grade Resonant MEMS Accelerometer. J. Microelectromech. Syst 2014, 23, 768–770. [Google Scholar]
- Xia, G.M.; Zhao, Y.; Zhao, J.; Shi, Q.; Qiu, A.P. Silicon vibrating beam accelerometer with ppm grade scale factor stability and tens-ppm grade full-range nonlinearity. In Proceedings of the 2016 IEEE International Symposium on Inertial Sensors and Systems, Laguna Beach, CA, USA, 22–25 February 2016. [Google Scholar]
- Zhao, J.; Wang, X.; Zhao, Y.; Xia, G.M.; Qiu, A.P.; Su, Y.; Xu, Y.P. A 0.23 μg Bias Instability and 1 μg/√Hz Acceleration Noise Density Silicon Oscillating Accelerometer With Embedded Frequency-to-Digital Converter in PLL. IEEE J. Solid-State Circuits 2017, 52, 1053–1065. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Y.P.; Xia, G.M.; Zhao, Y.; Zhao, J.; Qiu, A.P.; Su, Y. A 27μW MEMS silicon oscillating accelerometer with bias instability and 10-μg/√Hz noise floor. In Proceedings of the 2018 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Lake Como, Italy, 26–29 March 2018. [Google Scholar]
- Tocchio, A.; Caspani, A.; Langfelder, G.; Longoni, A.; Lasalandra, E. A Pierce oscillator for MEMS resonant accelerometer with a novel low-power amplitude limiting technique. In Proceedings of the 2012 IEEE International Frequency Control Symposium Proceedings, Baltimore, MD, USA, 21–24 May 2012. [Google Scholar]
- Allan, D.W. Time and Frequency (Time-Domain) Characterization, Estimation, and Prediction of Precision Clocks and Oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1987, 34, 647–654. [Google Scholar] [CrossRef] [PubMed]
- Pizzarulli, A.; Senatore, R.; Quatraro, E.; Perlmutter, M. Selecting the optimum inertial sensor for each specific application-A comprehensive guide based on analytic criteria and experimental data across several sensors and technologies. In Proceedings of the Position, Location and Navigation Symposium (PLANS), Monterey, CA, USA, 5–8 May 2014; pp. 519–523. [Google Scholar]
- Shin, D.; Chen, Y.; Flader, I.; Kenny, T. Temperature compensation of resonant accelerometer via nonlinear operation. In Proceedings of the 2018 IEEE Micro Electro Mechanical Systems (MEMS), Belfast, UK, 21–25 January 2018. [Google Scholar]
- Shin, D.; Chen, Y.; Flader, I.; Kenny, T. Epitaxially encapsulated resonant accelerometer with an on-chip micro-oven. In Proceedings of the 2017 19th International Conference on Solid-State Sensors, Actuators and Microsystems (TRANSDUCERS), Kaohsiung, Taiwan, 18–22 June 2017. [Google Scholar]
- Shin, D.; Ahn, C.H.; Chen, Y.; Christensen, D.; Flader, I.; Kenny, T. Environmentally robust differential resonant accelerometer in a wafer-scale encapsulation process. In Proceedings of the 2017 IEEE 30th International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, USA, 22–26 January 2017. [Google Scholar]
- Hopkins, R.; Miola, J.; Setterlund, R. The silicon oscillating accelerometer: A high-performance MEMS accelerometer for precision navigation and strategic guidance applications. In Proceedings of the Annual Meeting of the Institute of Navigation, San Diego, CA, USA, 24–26 January 2005; pp. 1043–1052. [Google Scholar]
- He, L.; Xu, Y.P.; Palaniapan, M. A CMOS Readout Circuit for SOI Resonant Accelerometer With 4-μg Bias Stability and 20-μg√Hz Resolution. IEEE J. Solid-State Circuits 2008, 43, 1480–1490. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, J.; Zhao, Y.; Xia, G.M.; Qiu, A.P.; Su, Y.; Xu, Y.P. A 0.4μg Bias Instability and 1.2μg/√Hz Noise Floor MEMS Silicon Oscillating Accelerometer With CMOS Readout Circuit. IEEE J. Solid-State Circuits 2017, 52, 472–482. [Google Scholar] [CrossRef]
- Sobreviela, G.; Riverola, M.; Uranga, A.; Barniol, N. Noise effects on resonator bias polarization in CMOS-MEMS oscillators. In Proceedings of the IEEE SENSORS, Valencia, Spain, 2–5 November 2014. [Google Scholar]
- Bahl, G.; Salvia, J.; Melamud, R.; Kim, B.; Howe, R.; Kenny, T. AC Polarization for Charge-Drift Elimination in Resonant Electrostatic MEMS and Oscillators. J. Microelectromech. Syst. 2011, 20, 355–364. [Google Scholar] [CrossRef]
- Hao, Q.; Yu, H.J.; Bei, P.; Peng, P.; Wu, Z. Attenuation of the dielectric charging-induced drift in capacitive accelerometer by AC bias voltage. J. Micro/ Nanolithography Mems & Moems 2017, 16, 1–8. [Google Scholar]
- Zhao, C.; Sobreviela, G.; Pandit, M.; Mustafazade, A.; Du, S.; Zou, X.; Seshia, A. A Resonant MEMS Accelerometer Utilizing AC Polarization. In Proceedings of the 2018 IEEE International Frequency Control Symposium (IFCS), Olympic Valley, CA, USA, 21–24 May 2018. [Google Scholar]
- Zhao, Y.; Zhao, J.; Wang, X.; Xia, G.M.; Qiu, A.P.; Su, Y.; Xu, Y.P. A Sub-µg Bias-Instability MEMS Oscillating Accelerometer With an Ultra-Low-Noise Read-Out Circuit in CMOS. IEEE J. Solid-State Circuits 2015, 50, 2113–2126. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, Y.; Wang, X.; Xia, G.M.; Qiu, A.P.; Su, Y.; Xu, Y.P. A System Decomposition Model for Phase Noise in Silicon Oscillating Accelerometers. IEEE J. Sensors 2016, 16, 5259–5269. [Google Scholar] [CrossRef]
- Colinet, E.; Arcamone, J.; Niel, A.; Lorent, E.; Hentz, S.; Ollier, E. 100 MHz oscillator based on a low polarization voltage capacitive Lamé-mode MEMS resonator. In Proceedings of the 2010 IEEE International Frequency Control Symposium (IFCS), Newport Beach, CA, USA, 1–4 June 2010. [Google Scholar]
- Zhao, Y.; Zhao, J.; Wang, X.; Xia, G.M.; Shi, Q.; Qiu, A.P.; Xu, Y.P. A Sub-0.1°/h Bias-Instability Split-Mode MEMS Gyroscope With CMOS Readout Circuit. IEEE J. Solid-State Circuits 2018, 53, 2636–2650. [Google Scholar] [CrossRef]
- Comi, C.; Corigliano, A.; Langfelder, G.; Longoni, A.; Tocchio, A.; Simoni, B. A Resonant Microaccelerometer With High Sensitivity Operating in an Oscillating Circuit. J. Microelectromech. Syst 2010, 19, 1140–1152. [Google Scholar] [CrossRef]
- Rogers, J.W.M.; Rahn, D.; Plett, C. A study of digital and analog automatic-amplitude control circuitry for voltage-controlled oscillators. IEEE J. Solid-State Circuits 2003, 38, 352–356. [Google Scholar] [CrossRef]
- IEEE Standards Association. Std 528-2001 IEEE Standard for Inertial Sensor Terminology; IEEE Standards Association: Piscataway, NJ, USA, 2001; pp. 1–26. [Google Scholar]






© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Xia, G.; Shi, Q.; Qiu, A. Expanding Bias-instability of MEMS Silicon Oscillating Accelerometer Utilizing AC Polarization and Self-Compensation. Sensors 2020, 20, 1455. https://doi.org/10.3390/s20051455
Zhao Y, Xia G, Shi Q, Qiu A. Expanding Bias-instability of MEMS Silicon Oscillating Accelerometer Utilizing AC Polarization and Self-Compensation. Sensors. 2020; 20(5):1455. https://doi.org/10.3390/s20051455
Chicago/Turabian StyleZhao, Yang, Guoming Xia, Qin Shi, and Anping Qiu. 2020. "Expanding Bias-instability of MEMS Silicon Oscillating Accelerometer Utilizing AC Polarization and Self-Compensation" Sensors 20, no. 5: 1455. https://doi.org/10.3390/s20051455
APA StyleZhao, Y., Xia, G., Shi, Q., & Qiu, A. (2020). Expanding Bias-instability of MEMS Silicon Oscillating Accelerometer Utilizing AC Polarization and Self-Compensation. Sensors, 20(5), 1455. https://doi.org/10.3390/s20051455



