Improving the Heading Accuracy in Indoor Pedestrian Navigation Based on a Decision Tree and Kalman Filter
Abstract
:1. Introduction
2. Classification of Magnetic Data with a Decision Tree
2.1. Geomagnetic Information Analysis
2.2. Decision Tree for Extracting geomagnetic Field Data
3. Heading Algorithm Based on a Decision Tree and the Kalman Filter
3.1. Attitude Angle Error Equation
3.2. Observation Equation Using Magnetic Data from Decision Tree
4. Results and Discussion
4.1. Experimental Equipment and Test Environment
4.2. Pedestrian Stride Estimate
4.3. Test and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, B.; Su, T.; Jin, X.; Kong, J.; Bai, Y. 3D Reconstruction of Pedestrian Trajectory with Moving Direction Learning and Optimal Gait Recognition. Complexity 2018, 2018, 10. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.; Al-Hamad, A.; Georgy, J.; Chang, H.W.; Inst, N. Portable Device Use Case Recognition Technique for Pedestrian Navigation. In Proceedings of the 28th International Technical Meeting of the Satellite Division of the Institute of Navigation; Institute of Navigation: Washington, WA, USA, 2015; pp. 202–208. [Google Scholar]
- Bojja, J.; Kirkko-Jaakkola, M.; Collin, J.; Takala, J. Indoor Localization Methods Using Dead Reckoning and 3D Map Matching. J. Signal Process. Syst. Signal Image Video Technol. 2014, 76, 301–312. [Google Scholar] [CrossRef]
- Uradzinski, M.; Guo, H.; Liu, X.K.; Yu, M. Advanced Indoor Positioning Using Zigbee Wireless Technology. Wirel. Pers. Commun. 2017, 97, 6509–6518. [Google Scholar] [CrossRef]
- Gu, F.; Hu, X.; Ramezani, M.; Acharya, D.; Khoshelham, K.; Valaee, S.; Shang, J. Indoor Localization Improved by Spatial Context - A Survey. Acm Comput. Surv. 2019, 52, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Harle, R. A Survey of Indoor Inertial Positioning Systems for Pedestrians. IEEE Commun. Surv. Tutor. 2013, 15, 1281–1293. [Google Scholar] [CrossRef]
- Ebner, F.; Fetzer, T.; Deinzer, F.; Grzegorzek, M. On Wi-Fi Model Optimizations for Smartphone-Based Indoor Localization. Isprs Int. Geo-Inf. 2017, 6, 223. [Google Scholar] [CrossRef] [Green Version]
- Li, X. RSS-Based Location Estimation with Unknown Pathloss Model. IEEE Trans. Wirel. Commun. 2006, 5, 3626–3633. [Google Scholar] [CrossRef]
- Jacq, D.; Chatonnay, P.; Bloch, C.; Canalda, P.; Spies, F. Towards zero-configuration for Wi-Fi indoor positioning system. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017; pp. 1–8. [Google Scholar]
- Meng, W.; Xiao, W.; Ni, W.; Xie, L. Secure and robust Wi-Fi fingerprinting indoor localization. In Proceedings of the 2011 International Conference on Indoor Positioning and Indoor Navigation, Guimaraes, Portugal, 21–23 September 2011; pp. 1–7. [Google Scholar]
- Correa, A.; Diaz, E.M.; Ahmed, D.B.; Morell, A.; Vicario, J.L. Advanced Pedestrian Positioning System to Smartphones and Smartwatches. Sensors 2016, 16, 1903. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Glover, M.; Yang, C.; Li, C.; Li, Z.; Cangelosi, A. Development of an Immersive Interface for Robot Teleoperation. In Proceedings of the Annual Conference towards Autonomous Robotic Systems, Guildford, UK, 19–21 July 2017; 2017; pp. 1–15. [Google Scholar]
- Lu, C.; Uchiyama, H.; Thomas, D.; Shimada, A.; Taniguchi, R.-i. Indoor Positioning System Based on Chest-Mounted IMU. Sensors 2019, 19, 420. [Google Scholar] [CrossRef] [Green Version]
- Tian, Z.S.; Zhang, Y.; Zhou, M.; Liu, Y. Pedestrian dead reckoning for MARG navigation using a smartphone. Eurasip J. Adv. Signal Process. 2014, 65. [Google Scholar] [CrossRef] [Green Version]
- Khedr, M.; El-Sheimy, N. A Smartphone Step Counter Using IMU and Magnetometer for Navigation and Health Monitoring Applications. Sensors 2017, 17, 2573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Foxlin, E. Pedestrian tracking with shoe-mounted inertial sensors. IEEE Comput. Graph. Appl. 2005, 25, 38–46. [Google Scholar] [CrossRef]
- Tjhai, C.; Keefe, K.O. Comparing Heading Estimates from Multiple Wearable Inertial and Magnetic Sensors Mounted on Lower Limbs. In Proceedings of the 2018 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 206–212. [Google Scholar]
- Afzal, M.H.; Renaudin, V.; Lachapelle, G. Assessment of Indoor Magnetic Field Anomalies using Multiple Magnetometers. In Proceedings of the 23rd International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2010), Portland, OR, USA, 21–24 September 2010; pp. 525–533. [Google Scholar]
- Song, J.W.; Park, C.G. Enhanced Pedestrian Navigation Based on Course Angle Error Estimation Using Cascaded Kalman Filters. Sensors 2018, 18, 1281. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Afzal, M.H.; Renaudin, V.; Lachapelle, G. Use of Earth’s Magnetic Field for Mitigating Gyroscope Errors Regardless of Magnetic Perturbation. Sensors 2011, 11, 11390–11414. [Google Scholar] [CrossRef] [PubMed]
- Bancroft, J.B.; Lachapelle, G. Use of Magnetic Quasi Static Field (QSF) Updates for Pedestrian Navigation. In Proceedings of the 2012 IEEE/Ion Position Location and Navigation Symposium, Myrtle Beach, SC, USA, 23–26 April 2012; pp. 605–612. [Google Scholar]
- Zhang, W.; Wei, D.; Gong, P.; Yuan, H. The PDR System Based on Improved QSF+ Map Matching Algorithm. In China Satellite Navigation Conference (CSNC) 2018 Proceedings; Springer: Singapore, 2018; pp. 753–764. [Google Scholar]
- Kim, J.; Hwang, M.; Jeong, D.-H.; Jung, H. Technology trends analysis and forecasting application based on decision tree and statistical feature analysis. Expert Syst. Appl. 2012, 39, 12618–12625. [Google Scholar] [CrossRef]
- Li, C.; Yang, C.; Wan, J.; Annamalai, A.; Cangelosi, A. Neural learning and Kalman filtering enhanced teaching by demonstration for a Baxter robot. In Proceedings of the 2017 23rd International Conference on Automation and Computing (ICAC), Huddersfield, UK, 7–8 September 2017; pp. 1–6. [Google Scholar]
- Rokach, L.; Maimon, O. Top-down induction of decision trees classifiers—A survey. IEEE Trans. Syst. Manand Cybern. Part C (Appl. Rev.) 2005, 35, 476–487. [Google Scholar] [CrossRef] [Green Version]
- Chiang, K.W.; Liao, J.K.; Tsai, G.J.; Chang, H.W. The Performance Analysis of the Map-Aided Fuzzy Decision Tree Based on the Pedestrian Dead Reckoning Algorithm in an Indoor Environment. Sensors 2016, 16, 34. [Google Scholar] [CrossRef] [Green Version]
- Deng, Z.A.; Wang, G.F.; Hu, Y.; Cui, Y. Carrying Position Independent User Heading Estimation for Indoor Pedestrian Navigation with Smartphones. Sensors 2016, 16, 677. [Google Scholar] [CrossRef] [Green Version]
- The World Magnetic Model. Available online: https://www.ngdc.noaa.gov/geomag/WMM/ (accessed on 12 October 2019).
- Klipp, K.; Rosé, H.; Willaredt, J.; Sawade, O.; Radusch, I. Rotation-Invariant Magnetic Features for Inertial Indoor-Localization. In Proceedings of the 2018 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Nantes, France, 24–27 September 2018; pp. 1–10. [Google Scholar]
- Renaudin, V.; Afzal, M.H.; Lachapelle, G. Complete Triaxis Magnetometer Calibration in the Magnetic Domain. J. Sens. 2010, 2010, 10. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Yang, G. Calibration of Miniature Inertial and Magnetic Sensor Units for Robust Attitude Estimation. IEEE Trans. Instrum. Meas. 2014, 63, 711–718. [Google Scholar] [CrossRef]
- Afzal, M.H. Use of Earth’s Magnetic Field for Pedestrian Navigation. Ph.D Thesis, University of Calgary, Calgary, AB, Canada, 2011. [Google Scholar]
- Jaehyun, P.; Yunki, K.; Jangmyung, L. Waist mounted Pedestrian Dead-Reckoning system. In Proceedings of the 2012 9th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Daejeon, Korea, 26–28 November 2012; pp. 335–336. [Google Scholar]
- Diaz, E.M.; Gonzalez, A.L.M. Step Detector and Step Length Estimator for an Inertial Pocket Navigation System. In 2014 International Conference on Indoor Positioning and Indoor Navigation; IEEE: New York, NY, USA, 2014; pp. 105–110. [Google Scholar]
- Weinberg, H. Using the ADXL202 in Pedometer and Personal Navigation Applications. Analog Devices -602 Appl. Note 2002, 2, 1–6. [Google Scholar]





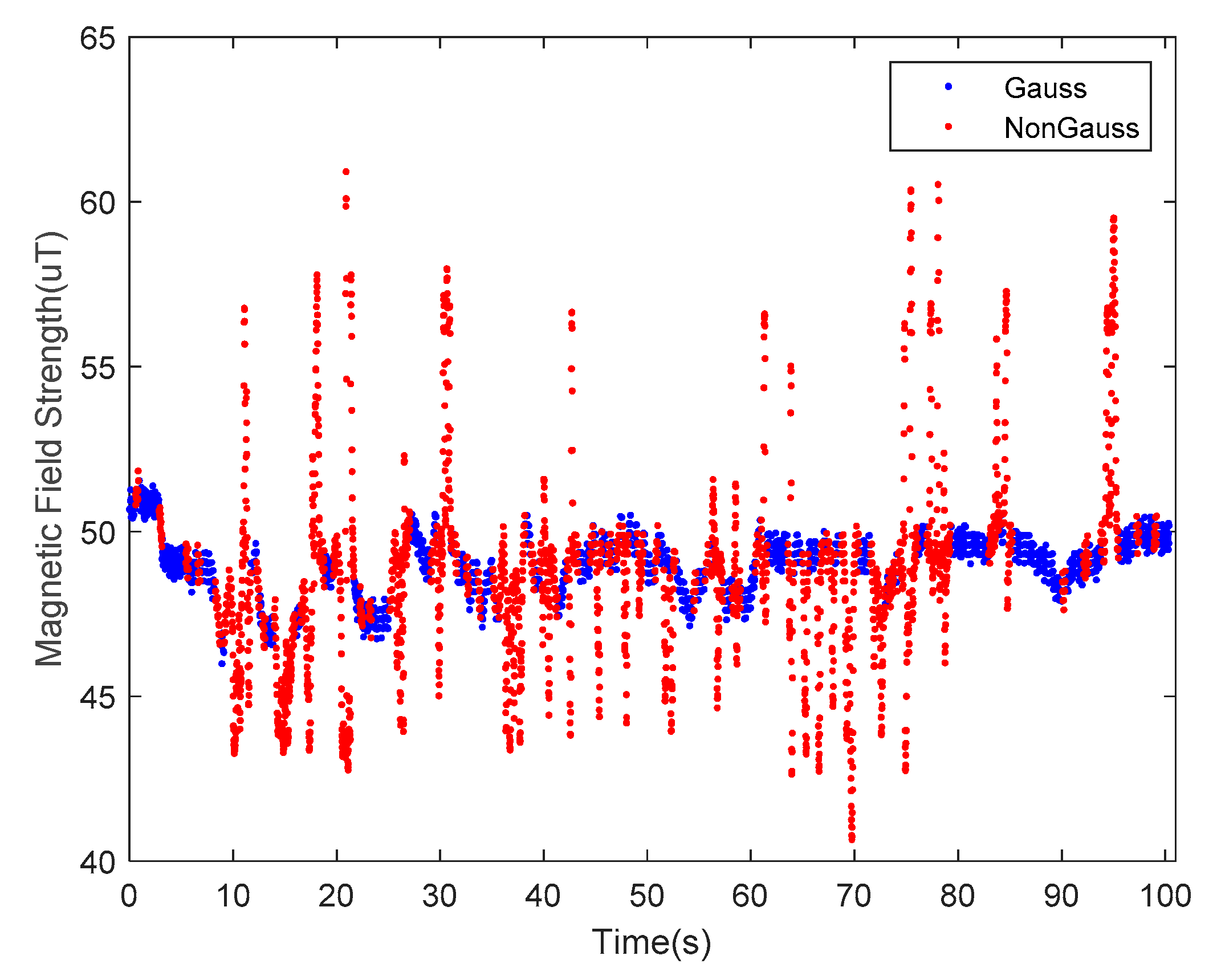
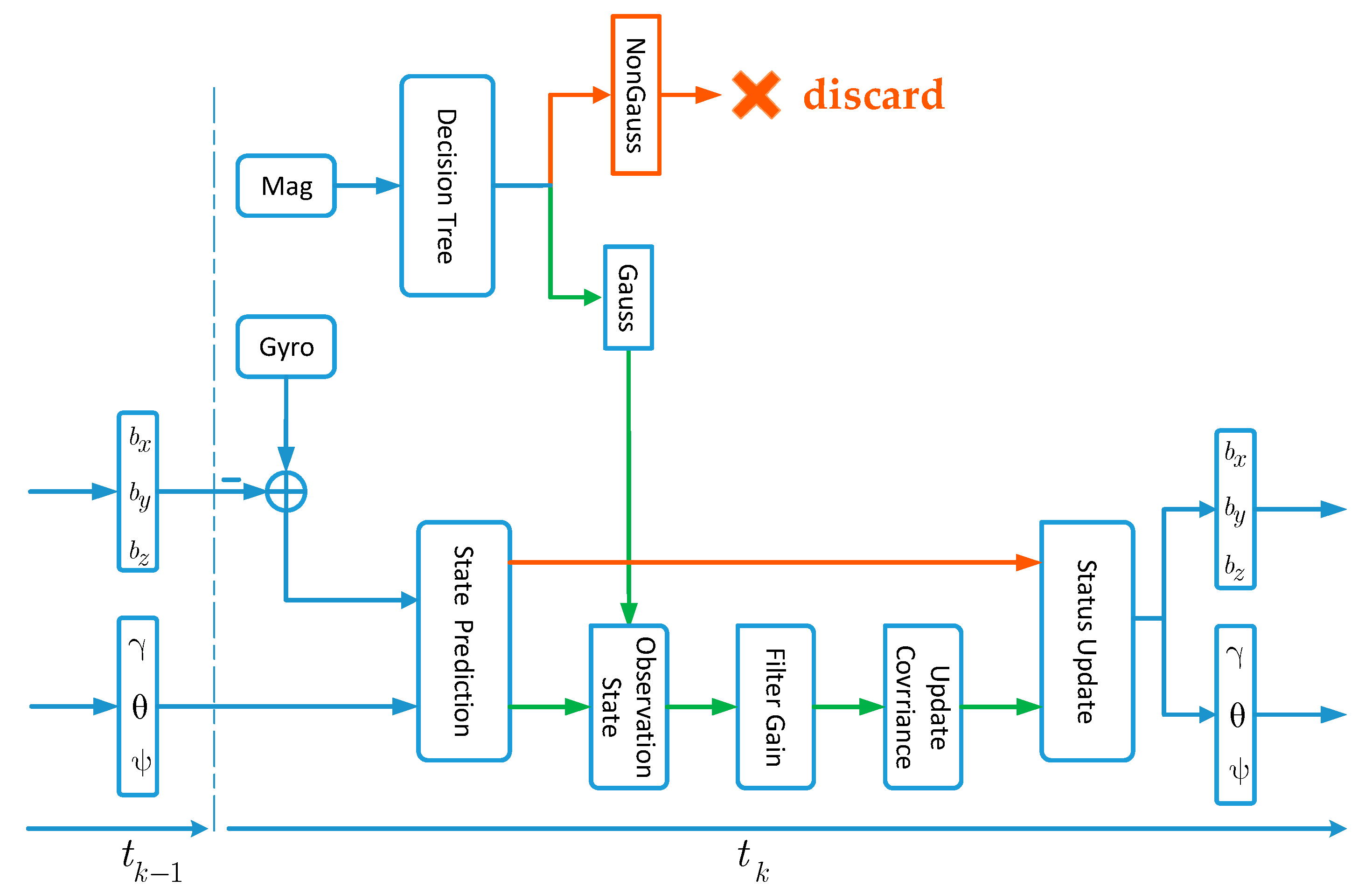


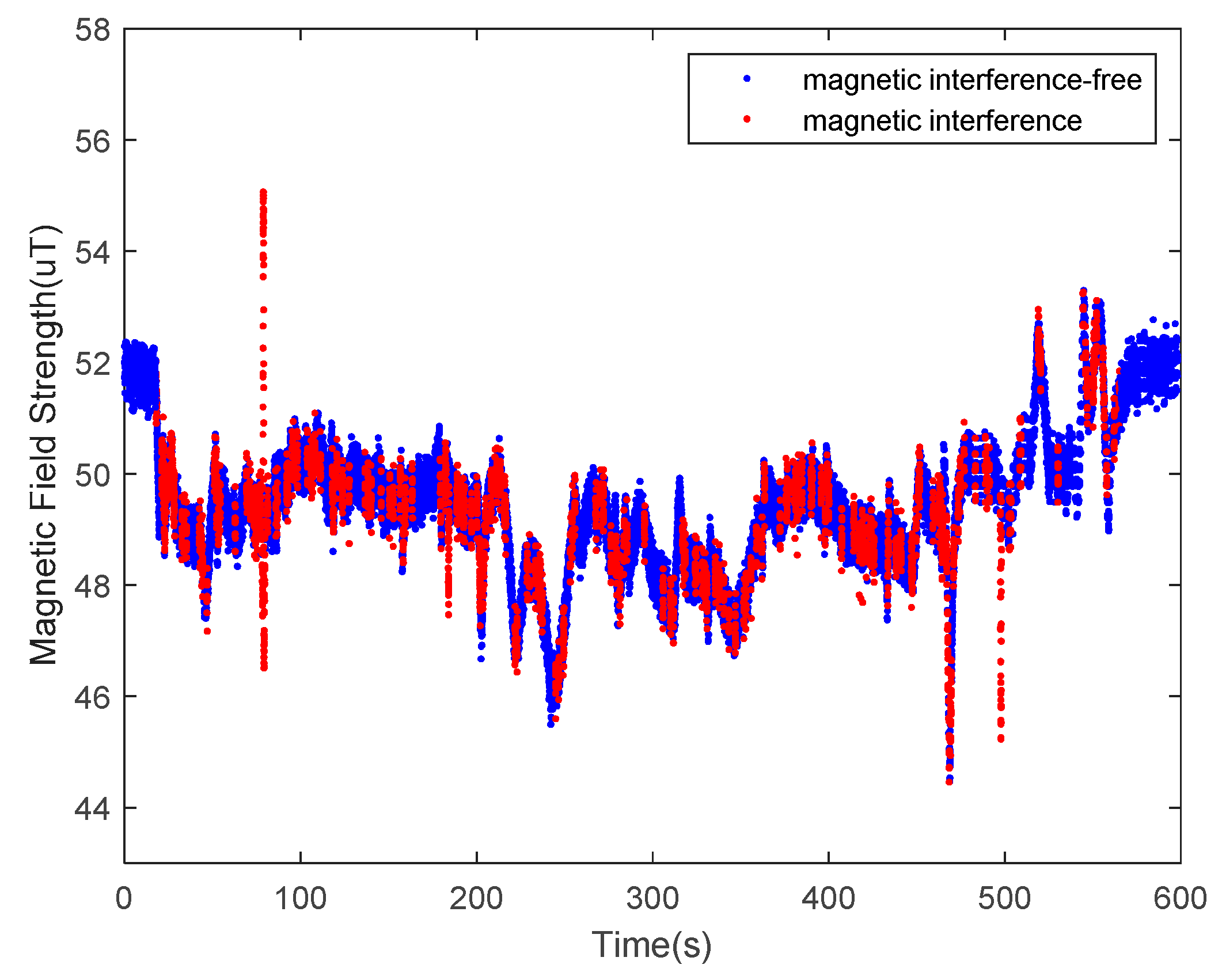









| No. | Fluctuation | Consistency | Gauss(Y/N) |
|---|---|---|---|
| 1 | a1 | b1 | Y |
| 2 | a2 | b2 | N |
| 3 | a3 | b3 | Y |
| 4 | a4 | b4 | N |
| n | an | bn | N |
| Sensors | Gyroscope | Accelerometer | Magnetometer |
|---|---|---|---|
| Standard full range | 500 deg/s | 8 g | 8 Gauss |
| Sensitivity | 65.6 LSB/deg/s | 1024 LSB/g | 4.35 milligauss |
| Noise Density | 0.007 deg/s/ (@10 Hz) | 120 ug/ | - |
| Noise Floor | 0.07 deg/s (@200 Hz) | - | 2 milligauss |
| Non-linearity | 0.1% FS | 0.5% FS | 0.1% FS |
| Cross-Axis Sensitivity | 2% | 1% | 0.2% FS/Gauss |
| Test Method | Gyro | Kalman | DT+Kalman |
|---|---|---|---|
| End point error | 201.57 m | 6.41 m | 3.04 m |
| Test Method | Gyro | Kalman | DT+Kalman |
|---|---|---|---|
| End point error | 7.53 m | 4.61 m | 1.17 m |
| Test Method | Kalman | GLRT+Kalman | DT+Kalman |
|---|---|---|---|
| End point error | 2.78 m | 1.88 m | 1.32 m |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Zhang, W.; Wan, H.; Li, X. Improving the Heading Accuracy in Indoor Pedestrian Navigation Based on a Decision Tree and Kalman Filter. Sensors 2020, 20, 1578. https://doi.org/10.3390/s20061578
Hu G, Zhang W, Wan H, Li X. Improving the Heading Accuracy in Indoor Pedestrian Navigation Based on a Decision Tree and Kalman Filter. Sensors. 2020; 20(6):1578. https://doi.org/10.3390/s20061578
Chicago/Turabian StyleHu, Guanghui, Weizhi Zhang, Hong Wan, and Xinxin Li. 2020. "Improving the Heading Accuracy in Indoor Pedestrian Navigation Based on a Decision Tree and Kalman Filter" Sensors 20, no. 6: 1578. https://doi.org/10.3390/s20061578
APA StyleHu, G., Zhang, W., Wan, H., & Li, X. (2020). Improving the Heading Accuracy in Indoor Pedestrian Navigation Based on a Decision Tree and Kalman Filter. Sensors, 20(6), 1578. https://doi.org/10.3390/s20061578





