Impacts of Imperfect Channel State Information, Transceiver Hardware, and Self-Interference Cancellation on the Performance of Full-Duplex MIMO Relay System
Abstract
:1. Introduction
2. System Model
3. Performance Analysis
3.1. Outage Probability Analysis
3.2. Ergodic Capacity Analysis
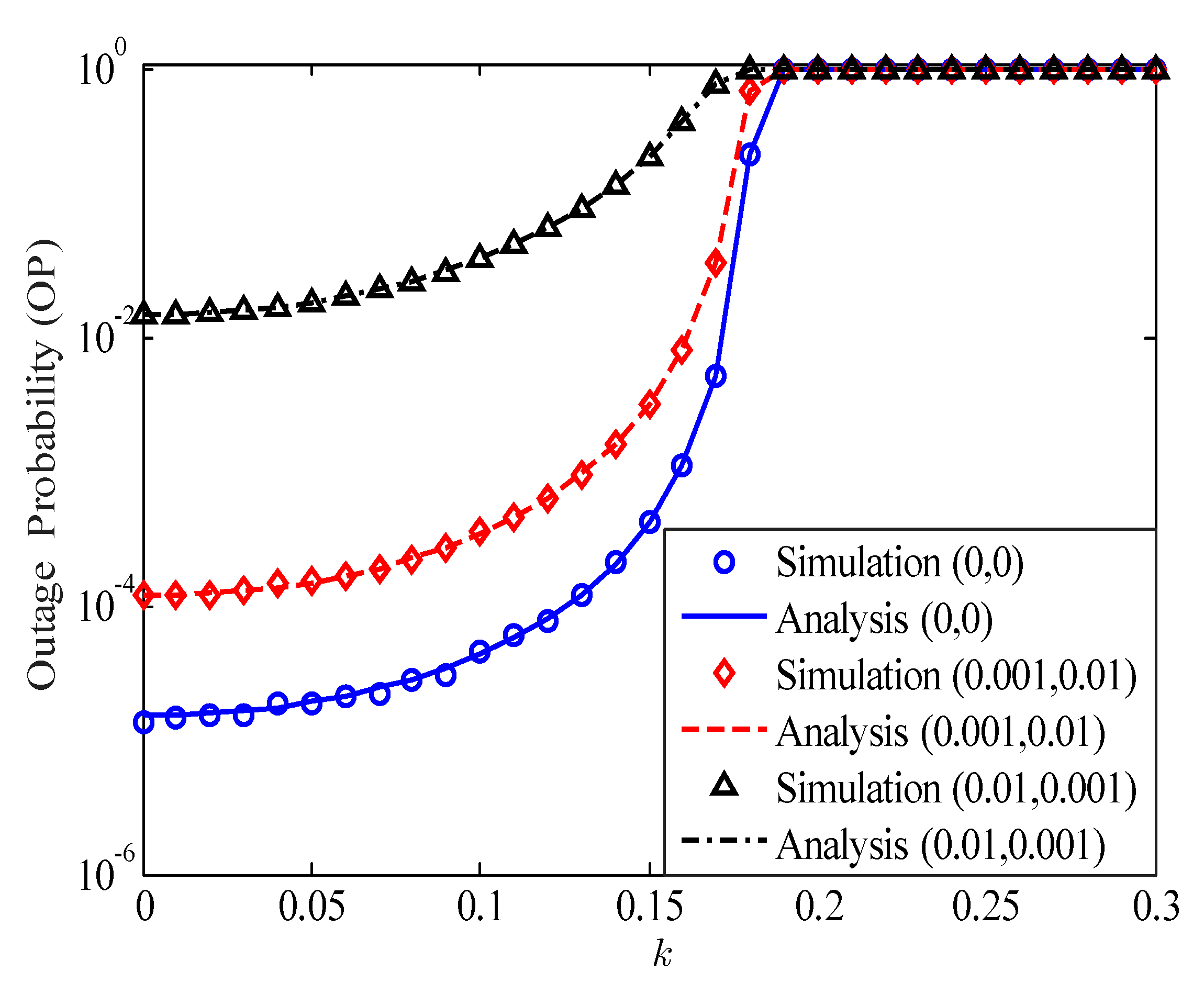
4. Numerical Results and Discussions
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Deng, Y.; Kim, K.J.; Duong, T.Q.; Elkashlan, M.; Karagiannidis, G.K.; Nallanathan, A. Full-Duplex Spectrum Sharing in Cooperative Single Carrier Systems. IEEE Trans. Cogn. Commun. Netw. 2016, 2, 68–82. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, B.C.; Tran, X.N.; Tran, D.T. Full-duplex amplify-and-forward relay system with direct link: Performance analysis and optimization. Phys. Commun. 2019, 37, 100888. [Google Scholar] [CrossRef]
- Gazestani, A.H.; Ghorashi, S.A.; Mousavinasab, B.; Shikh-Bahaei, M. A Survey on Implementation and Applications of Full Duplex Wireless Communications. Phys. Commun. 2019, 34, 121–134. [Google Scholar] [CrossRef]
- Doan, X.T.; Nguyen, N.P.; Yin, C.; Da Costa, D.B.; Duong, T.Q. Cognitive full-duplex relay networks under the peak interference power constraint of multiple primary users. EURASIP J. Wirel. Commun. Netw. 2017, 2017, 8. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, L.V.; Nguyen, B.C.; Tran, X.N.; Dung, L.T. Closed-Form Expression for the Symbol Error Probability in Full-Duplex Spatial Modulation Relay System and Its Application in Optimal Power Allocation. Sensors 2019, 19, 5390. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, B.C.; Tran, X.N.; Tran, D.T. Performance analysis of in-band full-duplex amplify-and-forward relay system with direct link. In Proceedings of the 3rd International Conference on Recent Advances in Signal Processing, Ho Chi Minh, Vietnam, 29–31 January 2018; pp. 192–197. [Google Scholar]
- Ji, B.; Chen, Z.; Chen, S.; Zhou, B.; Li, C.; Wen, H. Joint optimization for ambient backscatter communication system with energy harvesting for IoT. Mech. Syst. Signal Process. 2020, 135, 106412. [Google Scholar] [CrossRef]
- Ji, B.; Xing, B.; Song, K.; Li, C.; Wen, H.; Yang, L. The Efficient BackFi Transmission Design in Ambient Backscatter Communication Systems for IoT. IEEE Access 2019, 7, 31397–31408. [Google Scholar] [CrossRef]
- Ji, B.; Li, Y.; Zhou, B.; Li, C.; Song, K.; Wen, H. Performance Analysis of UAV Relay Assisted IoT Communication Network Enhanced With Energy Harvesting. IEEE Access 2019, 7, 38738–38747. [Google Scholar] [CrossRef]
- Ji, B.; Li, Y.; Chen, S.; Han, C.; Li, C.; Wen, H. Secrecy Outage Analysis of UAV Assisted Relay and Antenna Selection for Cognitive Network under Nakagami-m Channel. IEEE Trans. Cogn. Commun. Netw. 2020. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Kundu, C.; Ngo, H.Q.; Duong, T.Q.; Canberk, B. Secure full-duplex small-cell networks in a spectrum sharing environment. IEEE Access 2016, 4, 3087–3099. [Google Scholar] [CrossRef]
- Nguyen, N.P.; Ngo, H.Q.; Duong, T.Q.; Tuan, H.D.; da Costa, D.B. Full-Duplex Cyber-Weapon with Massive Arrays. IEEE Trans. Commun. 2017, 65, 5544–5558. [Google Scholar] [CrossRef] [Green Version]
- Tam, H.H.M.; Tuan, H.D.; Nasir, A.A.; Duong, T.Q.; Poor, H.V. MIMO Energy Harvesting in Full-Duplex Multi-User Networks. IEEE Trans. Wirel. Commun. 2017, 16, 3282–3297. [Google Scholar] [CrossRef] [Green Version]
- Coskun, A.F.; Kucur, O. Performance Analysis of Maximal-Ratio Transmission/Receive Antenna Selection in Nakagami-m Fading Channels with Channel Estimation Errors and Feedback Delay. IEEE Trans. Veh. Technol. 2012, 61, 1099–1108. [Google Scholar] [CrossRef]
- Rui, X. Analysis of MIMO MRT/SC Systems. Wirel. Pers. Commun. 2012, 62, 117–126. [Google Scholar] [CrossRef]
- Qin, D.; Wang, Y.; Zhou, T. Performance Analysis of AF Relays with Maximal Ratio Combining in Nakagami-Fading Environments. Wirel. Commun. Mob. Comput. 2019, 2019. [Google Scholar] [CrossRef]
- Wang, D.; Wang, M.; Zhu, P.; Li, J.; Wang, J.; You, X. Performance of Network-Assisted Full-Duplex for Cell-Free Massive MIMO. IEEE Trans. Commun. 2019. [Google Scholar] [CrossRef] [Green Version]
- Cai, Y.; Xu, Y.; Shi, Q.; Champagne, B.; Hanzo, L. Robust Joint Hybrid Transceiver Design for Millimeter Wave Full-Duplex MIMO Relay Systems. IEEE Trans. Wirel. Commun. 2019, 18, 1199–1215. [Google Scholar] [CrossRef]
- Eshteiwi, K.; Kaddoum, G.; Alam, M. Ergodic Capacity Analysis of Full Duplex Relaying in the Presence of Co-Channel Interference in V2V Communications. Sensors 2020, 20, 261. [Google Scholar] [CrossRef] [Green Version]
- Eshteiwi, K.; Kaddoum, G.; Fredj, K.B.; Soujeri, E.; Gagnon, F. Performance Analysis of Full-Duplex Vehicle Relay-Based Selection in Dense Multi-Lane Highways. IEEE Access 2019, 7, 61581–61595. [Google Scholar] [CrossRef]
- Almradi, A.; Hamdi, K.A. MIMO Full-Duplex Relaying in the Presence of Co-Channel Interference. IEEE Trans. Veh. Technol. 2016, 66, 4874–4885. [Google Scholar] [CrossRef] [Green Version]
- Day, B.P.; Margetts, A.R.; Bliss, D.W.; Schniter, P. Full-Duplex MIMO Relaying: Achievable Rates under Limited Dynamic Range. IEEE J. Sel. Areas Commun. 2012, 30, 1541. [Google Scholar] [CrossRef] [Green Version]
- Xie, W.; Xia, X.; Xu, Y.; Xu, K.; Wang, Y. Massive MIMO full-duplex relaying with hardware impairments. J. Commun. Netw. 2017, 19, 351–362. [Google Scholar] [CrossRef]
- Narayanan, S.; Ahmadi, H.; Flanagan, M.F. On the Performance of Spatial Modulation MIMO for Full-Duplex Relay Networks. IEEE Trans. Wirel. Commun. 2017, 16, 3727–3746. [Google Scholar] [CrossRef] [Green Version]
- Dey, S.; Sharma, E.; Budhiraja, R. Scaling Analysis of Hardware-Impaired Two-Way Full-Duplex Massive MIMO Relay. IEEE Commun. Lett. 2019, 23, 1249–1253. [Google Scholar] [CrossRef]
- Taghizadeh, O.; Cirik, A.C.; Mathar, R. Hardware Impairments Aware Transceiver Design for Full-Duplex Amplify-and-Forward MIMO Relaying. IEEE Trans. Wirel. Commun. 2017, 17, 1644–1659. [Google Scholar] [CrossRef] [Green Version]
- Everett, E.; Sahai, A.; Sabharwal, A. Passive Self-Interference Suppression for Full-Duplex Infrastructure Nodes. IEEE Trans. Wirel. Commun. 2014, 13, 680–694. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Wang, H.; Yao, Y.; Chen, Z.; Li, X.; Zhang, S. Outage Performance of the Full-Duplex Two-Way DF Relay System Under Imperfect CSI. IEEE Access 2017, 5, 5425–5435. [Google Scholar] [CrossRef]
- Tran, X.N.; Nguyen, B.C.; Tran, D.T. Outage Probability of Two-Way Full-Duplex Relay System with Hardware Impairments. In Proceedings of the 2019 3rd International Conference on Recent Advances in Signal Processing, Telecommunications & Computing (SigTelCom), Hanoi, Vietnam, 21–22 March 2019; pp. 135–139. [Google Scholar]
- Björnson, E.; Hoydis, J.; Kountouris, M.; Debbah, M. Massive MIMO Systems with Non-Ideal Hardware: Energy Efficiency, Estimation, and Capacity Limits. IEEE Trans. Inf. Theory 2014, 60, 7112–7139. [Google Scholar] [CrossRef] [Green Version]
- Papazafeiropoulos, A.; Sharma, S.K.; Ratnarajah, T.; Chatzinotas, S. Impact of Residual Additive Transceiver Hardware Impairments on Rayleigh-Product MIMO Channels with Linear Receivers: Exact and Asymptotic Analyses. IEEE Trans. Commun. 2017, 66, 105–118. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, B.C.; Tran, X.N. Performance Analysis of Full-Duplex Amplify-and-Forward Relay System with Hardware Impairments and Imperfect Self-Interference Cancellation. Wirel. Commun. Mob. Comput. 2019, 2019, 10. [Google Scholar] [CrossRef] [Green Version]
- Bharadia, D.; McMilin, E.; Katti, S. Full duplex radios. In ACM SIGCOMM Computer Communication Review; ACM: New York, NY, USA, 2013; Volume 43, pp. 375–386. [Google Scholar]
- Nguyen, B.C.; Hoang, T.M.; Tran, P.T.; Nguyen, T.N. Outage probability of NOMA system with wireless power transfer at source and full-duplex relay. AEU-Int. J. Electron. Commun. 2020, 116, 152957. [Google Scholar] [CrossRef]
- Li, S.; Kun, Y.; Zhou, M.; Wu, J.; Song, L.; Li, Y.; Li, H. Full-duplex Amplify-and-Forward Relaying: Power and Location Optimization. IEEE Trans. Veh. Technol. 2017. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, B.C.; Tran, X.N. Performance Analysis of Full-Duplex Spatial Modulation Systems With Transmit Antenna Selection. In Proceedings of the 2019 International Conference on Advanced Technologies for Communications (ATC), Hanoi, Vietnam, 17–19 October 2019; pp. 282–286. [Google Scholar]
- Goldsmith, A. Wireless Communications; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Leon-Garcia, A.; Leon-Garcia, A. Probability, Statistics, and Random Processes for Electrical Engineering; Pearson: Upper Saddle River, NJ, USA, 2008. [Google Scholar]
- Nguyen, B.C.; Tran, X.N. Transmit Antenna Selection for Full-Duplex Spatial Modulation Multiple-Input Multiple-Output System. IEEE Syst. J. 2020. [Google Scholar] [CrossRef]
- Jeffrey, A.; Zwillinger, D. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Modi, B.; Annamalai, A.; Olabiyi, O.; Palat, R. Ergodic capacity analysis of cooperative amplify-and-forward relay networks over generalized fading channels. Wirel. Commun. Mob. Comput. 2015, 15, 1259–1273. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; Dover: New York, NY, USA, 1972. [Google Scholar]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, B.C.; Thang, N.N.; Tran, X.N.; Dung, L.T. Impacts of Imperfect Channel State Information, Transceiver Hardware, and Self-Interference Cancellation on the Performance of Full-Duplex MIMO Relay System. Sensors 2020, 20, 1671. https://doi.org/10.3390/s20061671
Nguyen BC, Thang NN, Tran XN, Dung LT. Impacts of Imperfect Channel State Information, Transceiver Hardware, and Self-Interference Cancellation on the Performance of Full-Duplex MIMO Relay System. Sensors. 2020; 20(6):1671. https://doi.org/10.3390/s20061671
Chicago/Turabian StyleNguyen, Ba Cao, Nguyen Nhu Thang, Xuan Nam Tran, and Le The Dung. 2020. "Impacts of Imperfect Channel State Information, Transceiver Hardware, and Self-Interference Cancellation on the Performance of Full-Duplex MIMO Relay System" Sensors 20, no. 6: 1671. https://doi.org/10.3390/s20061671
APA StyleNguyen, B. C., Thang, N. N., Tran, X. N., & Dung, L. T. (2020). Impacts of Imperfect Channel State Information, Transceiver Hardware, and Self-Interference Cancellation on the Performance of Full-Duplex MIMO Relay System. Sensors, 20(6), 1671. https://doi.org/10.3390/s20061671




