Generative Adversarial Learning Enhanced Fault Diagnosis for Planetary Gearbox under Varying Working Conditions
Abstract
:1. Introduction
2. Generative Adversarial Learning Architecture
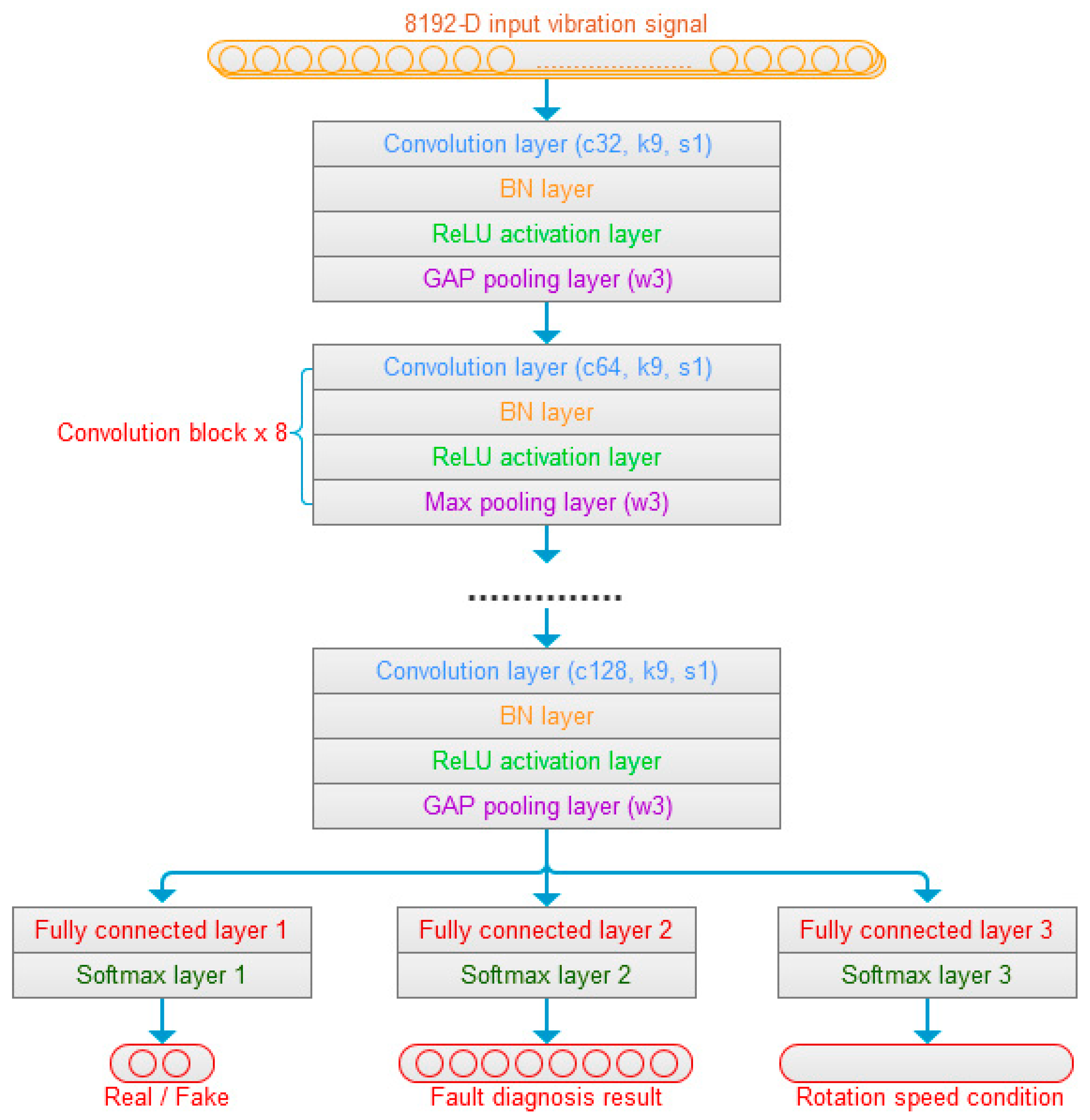
3. Fault Diagnosis Method Based on GAN Enhanced CNN
3.1. One-Dimensional Convolution of CNN
3.2. Batch Normalization
3.3. Rectified Linear Units Activation
3.4. Generator of Vibration Signal
3.5. Discriminator of Fault Diagnosis
4. Experiment Validation
4.1. Experiment of Vibration Signal Generation
4.2. Experiment of Fault Diagnosis in Target Domain
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lei, Y.; Tang, W.; Kong, D. Vibration signal simulation and fault diagnosis of planetary gearboxes based on transmission mechanism analysis. J. Mech. Eng. 2014, 50, 61–68. [Google Scholar] [CrossRef]
- Feng, Z.; Zuo, M.J. Vibration signal models for fault diagnosis of planetary gearboxes. J. Sound Vib. 2012, 331, 4919–4939. [Google Scholar] [CrossRef]
- Feng, Z.; Ma, H.; Zuo, M.J. Spectral negentropy based sidebands and demodulation analysis for planet bearing fault diagnosis. J. Sound Vib. 2017, 410, 124–150. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Artificial intelligence for the modeling and control of combustion processes: A review. Prog. Energy Combust. Sci. 2003, 29, 515–566. [Google Scholar] [CrossRef]
- Worden, K.; Staszewski, W.J.; Hensman, J.J. Natural computing for mechanical systems research: A tutorial overview. Mech. Syst. Signal Process. 2011, 25, 4–111. [Google Scholar] [CrossRef]
- Cheng, G.; Chen, X.; Li, H.; Liu, H. Study on planetary gear fault diagnosis based on entropy feature fusion of ensemble empirical mode decomposition. Measurement 2016, 91, 140–154. [Google Scholar] [CrossRef]
- Li, Y.; Li, G.; Yang, Y.; Liang, X.; Xu, M. A fault diagnosis scheme for planetary gearboxes using adaptive multi-scale morphology filter and modified hierarchical permutation entropy. Mech. Syst. Signal Process. 2018, 105, 319–337. [Google Scholar] [CrossRef]
- Lei, Y.; Liu, Z.; Wu, X.; Li, N.; Lin, J. Health condition identification of multi-stage planetary gearboxes using a mRVM-based method. Mech. Syst. Signal Process. 2015, 60, 289–300. [Google Scholar] [CrossRef]
- Zhang, W.; Itoh, K.; Tanida, J.; Xu, M. Parallel distributed processing model with local space-invariant interconnections and its optical architecture. Appl. Opt. 1990, 29, 4790–4797. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y. Convolutional neural networks for sentence classification. arXiv 2014, arXiv:1408.5882. [Google Scholar]
- Zhang, X.; Lecun, Y. Text understanding from scratch. arXiv 2015, arXiv:1502.01710. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2012, 60, 1097–1105. [Google Scholar] [CrossRef]
- Aghdam, H.H.; Heravi, E.J. Guide to Convolutional Neural Networks: A Practical Application to Traffic-Sign Detection and Classification; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Jia, F.; Lei, Y.; Lin, J. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72, 303–315. [Google Scholar] [CrossRef]
- Kane, P.V.; Andhare, A.B. Application of psychoacoustics for gear fault diagnosis using artificial neural network. J. Low Freq. NoiseVib. Act. Control 2016, 35, 207–220. [Google Scholar] [CrossRef] [Green Version]
- AlThobiani, F.; Ball, A. An approach to fault diagnosis of reciprocating compressor valves using Teager–Kaiser energy operator and deep belief networks. Expert Syst. Appl. 2014, 41, 4113–4122. [Google Scholar]
- Tamilselvan, P.; Wang, P. Failure diagnosis using deep belief learning based health state classification. Reliab. Eng. Syst. Saf. 2013, 115, 124–135. [Google Scholar] [CrossRef]
- Li, C.; Sánchez, R.V.; Zurita, G.; Cerrada, M.; Cabrera, D. Fault diagnosis for rotating machinery using vibration measurement deep statistical feature learning. Sensors 2016, 16, 895. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Amarnath, M.; Kankar, P.K. Feature extraction and fault severity classification in ball bearings. J. Vib. Control 2016, 22, 176–192. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Li, C.; Sanchez, R.V. Gearbox fault identification and classification with convolutional neural networks. Shock Vib. 2015, 2015, 390134. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Sanchez, R.V.; Zurita, G.; Cerrada, M.; Cabrera, D.; Vásquez, R.E. Multimodal deep support vector classification with homologous features and its application to gearbox fault diagnosis. Neurocomputing 2015, 168, 119–127. [Google Scholar] [CrossRef]
- Chen, Z.; Li, C.; Sánchez, R.V. Multi-layer neural network with deep belief network for gearbox fault diagnosis. J. Vibro Eng. 2015, 17, 2379–2392. [Google Scholar]
- Verma, N.K.; Gupta, V.K.; Sharma, M. Intelligent condition-based monitoring of rotating machines using sparse auto-encoders. In Proceedings of the Prognostics and Health Management (PHM), 2013 IEEE Conference on Prognostics and Health Management, Gaithersburg, MD, USA, 24–27 June 2013; pp. 1–7. [Google Scholar]
- Yang, Z.X.; Wang, X.B.; Zhong, J.H. Representational learning for fault diagnosis of wind turbine equipment: A multi-layered extreme learning machines approach. Energies 2016, 9, 379. [Google Scholar] [CrossRef] [Green Version]
- Gan, M.; Wang, C. Construction of hierarchical diagnosis network based on deep learning and its application in the fault pattern recognition of rolling element bearings. Mech. Syst. Signal Process. 2016, 72, 92–104. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, X.; Pei, J.; Tang, G. Transformer fault diagnosis using continuous sparse autoencoder. SpringerPlus 2016, 5, 448. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tamilselvan, P.; Wang, Y.; Wang, P. Deep belief network-based state classification for structural health diagnosis. Aerosp. Conf. 2012 IEEE 2012, 2012, 1–11. [Google Scholar]
- Shao, H.; Jiang, H.; Zhang, X.; Niu, M. Rolling bearing fault diagnosis using an optimization deep belief network. Meas. Sci. Technol. 2015, 26, 115002. [Google Scholar] [CrossRef]
- Lei, Y.; Jia, F.; Zhou, X. A deep learning-based method for machinery health monitoring with big data. J. Mech. Eng. 2015, 51, 49–56. [Google Scholar] [CrossRef]
- Janssens, O.; Slavkovikj, V.; Vervisch, B.; Stockman, K.; Loccufier, M.; Verstockt, S.; Van de Walle, R.; Van Hoecke, S. Convolutional neural network-based fault detection for rotating machinery. J. Sound Vib. 2016, 377, 331–345. [Google Scholar] [CrossRef]
- Jing, L.; Zhao, M.; Li, P.; Xu, X. A convolutional neural network-based feature learning and fault diagnosis method for the condition monitoring of gearbox. Measurement 2017, 111, 1–10. [Google Scholar] [CrossRef]
- Zhang, W.; Peng, G.; Li, C.; Zhang, Z. A New Deep Learning Model for Fault Diagnosis with Good Anti-Noise and Domain Adaptation Ability on Raw Vibration Signals. Sensors 2017, 17, 425. [Google Scholar] [CrossRef]
- Zhao, R.; Yan, R.; Chen, Z.; Mao, K.; Wang, P.; Gao, R.X. Deep learning and its applications to machine health monitoring. Mech. Syst. Signal Process. 2019, 115, 213–237. [Google Scholar] [CrossRef]
- Wang, H.; Li, S.; Song, L.; Cui, L. A novel convolutional neural network-based fault recognition method via image fusion of multi-vibration-signals. Comput. Ind. 2019, 105, 182–190. [Google Scholar] [CrossRef]
- Huang, R.; Liao, Y.; Zhang, S.; Li, W. Deep Decoupling Convolutional Neural Network for Intelligent Compound Fault Diagnosis. IEEE Access 2019, 7, 1848–1858. [Google Scholar] [CrossRef]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly Accurate Machine Fault Diagnosis Using Deep Transfer Learning. IEEE Trans. Ind. Inform. 2019, 15, 2446–2455. [Google Scholar] [CrossRef]
- Yang, B.; Lei, Y.; Jiang, F.; Xing, S. An intelligent fault diagnosis approach based on transfer learning from laboratory bearings to locomotive bearings. Mech. Syst. Signal Process. 2019, 122, 692–706. [Google Scholar] [CrossRef]
- Arjovsky, M.; Bottou, L. Towards Principled Methods for Training Generative Adversarial Networks. arXiv 2017, arXiv:1701.04862. [Google Scholar]
- Kodali, N.; Abernethy, J.; Hays, J. On Convergence and Stability of GANs. Proceedings of ICLR 2018 Conference, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]















| Parameter | Frequency (Hz) | ||||
|---|---|---|---|---|---|
| WC-A | WC-B | WC-C | WC-D | WC-E | |
| Sun gear rotation frequency | 25 | 20 | 15 | 10 | 5 |
| Planet gear meshing frequency | 546.88 | 437.47 | 328.1 | 218.74 | 109.37 |
| Planet carrier rotation frequency | 5.47 | 4.38 | 3.28 | 2.19 | 1.09 |
| Planet gear pass frequency | 21.88 | 17.50 | 13.13 | 8.75 | 4.38 |
| Planet gear rotation frequency | 9.72 | 7.78 | 5.83 | 3.89 | 1.94 |
| Faulty planet gear frequency | 15.19 | 12.15 | 9.11 | 6.08 | 3.04 |
| Source Domain | Target Domain | ||||
|---|---|---|---|---|---|
| WC-A | WC-B | WC-C | WC-E | WC-D | |
| classification accuracy | 83% | 88.3% | 85.3% | 95% | 78.7% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, W.; Bai, Y.; Cheng, W. Generative Adversarial Learning Enhanced Fault Diagnosis for Planetary Gearbox under Varying Working Conditions. Sensors 2020, 20, 1685. https://doi.org/10.3390/s20061685
Wen W, Bai Y, Cheng W. Generative Adversarial Learning Enhanced Fault Diagnosis for Planetary Gearbox under Varying Working Conditions. Sensors. 2020; 20(6):1685. https://doi.org/10.3390/s20061685
Chicago/Turabian StyleWen, Weigang, Yihao Bai, and Weidong Cheng. 2020. "Generative Adversarial Learning Enhanced Fault Diagnosis for Planetary Gearbox under Varying Working Conditions" Sensors 20, no. 6: 1685. https://doi.org/10.3390/s20061685




