A Novel Approach for Mixed Manual/Connected Automated Freeway Traffic Management
Abstract
:1. Introduction
2. Literature Review
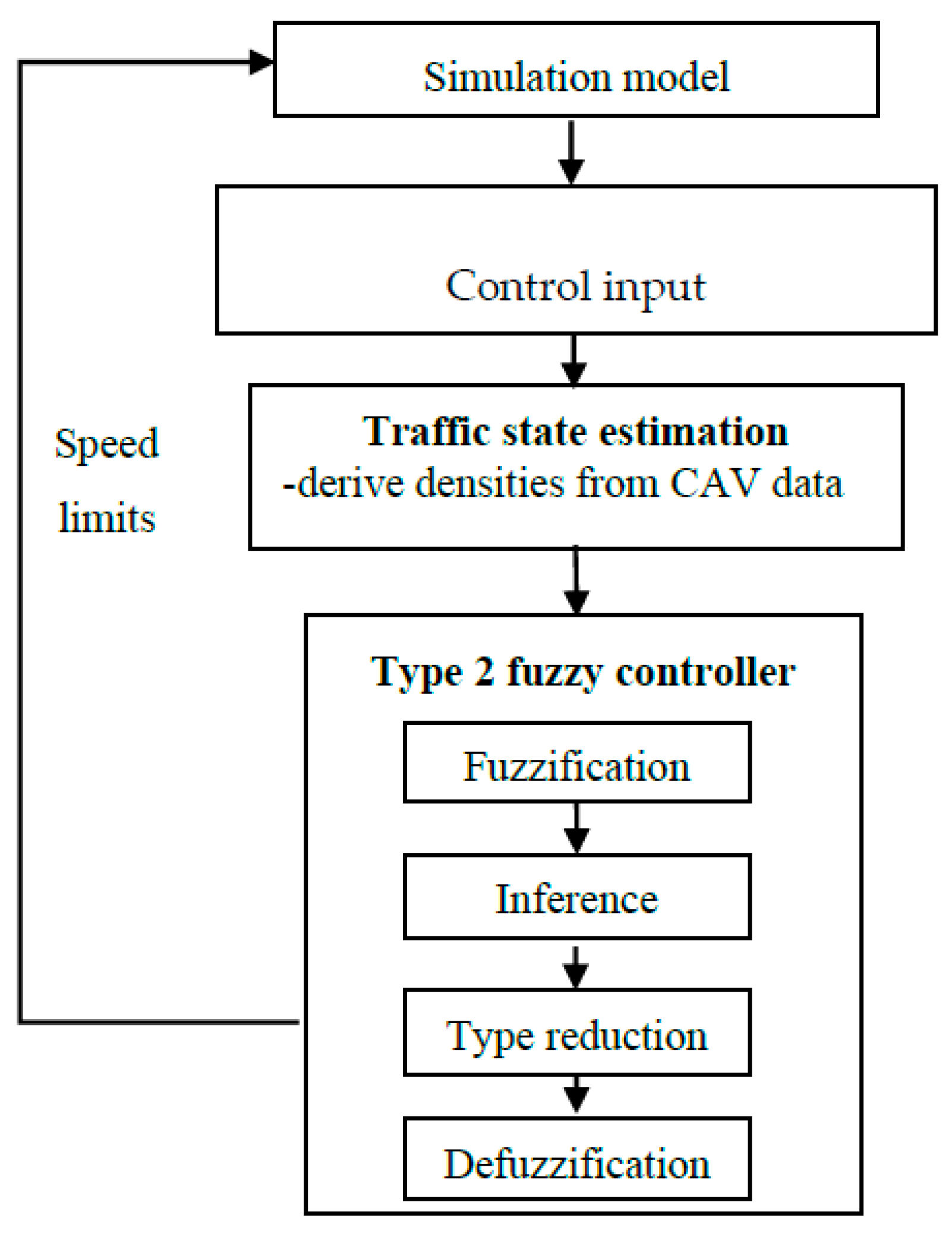
3. Methodology
3.1. Traffic State Estimation
3.2. Interval Type-2 Fuzzy Logic Control
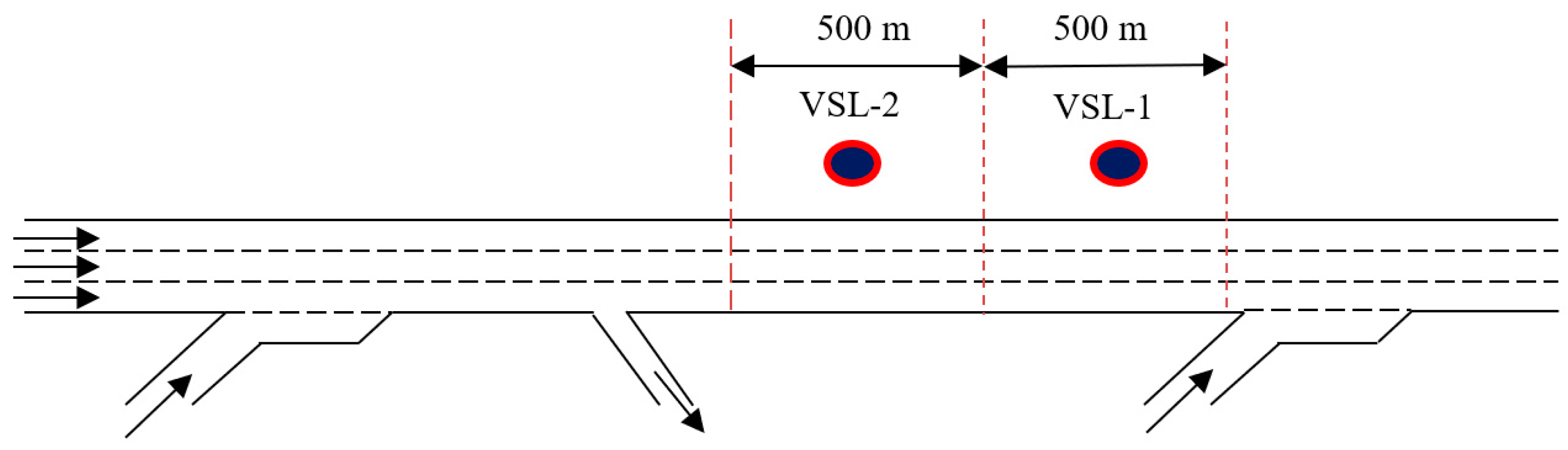
4. Simulation Experiment
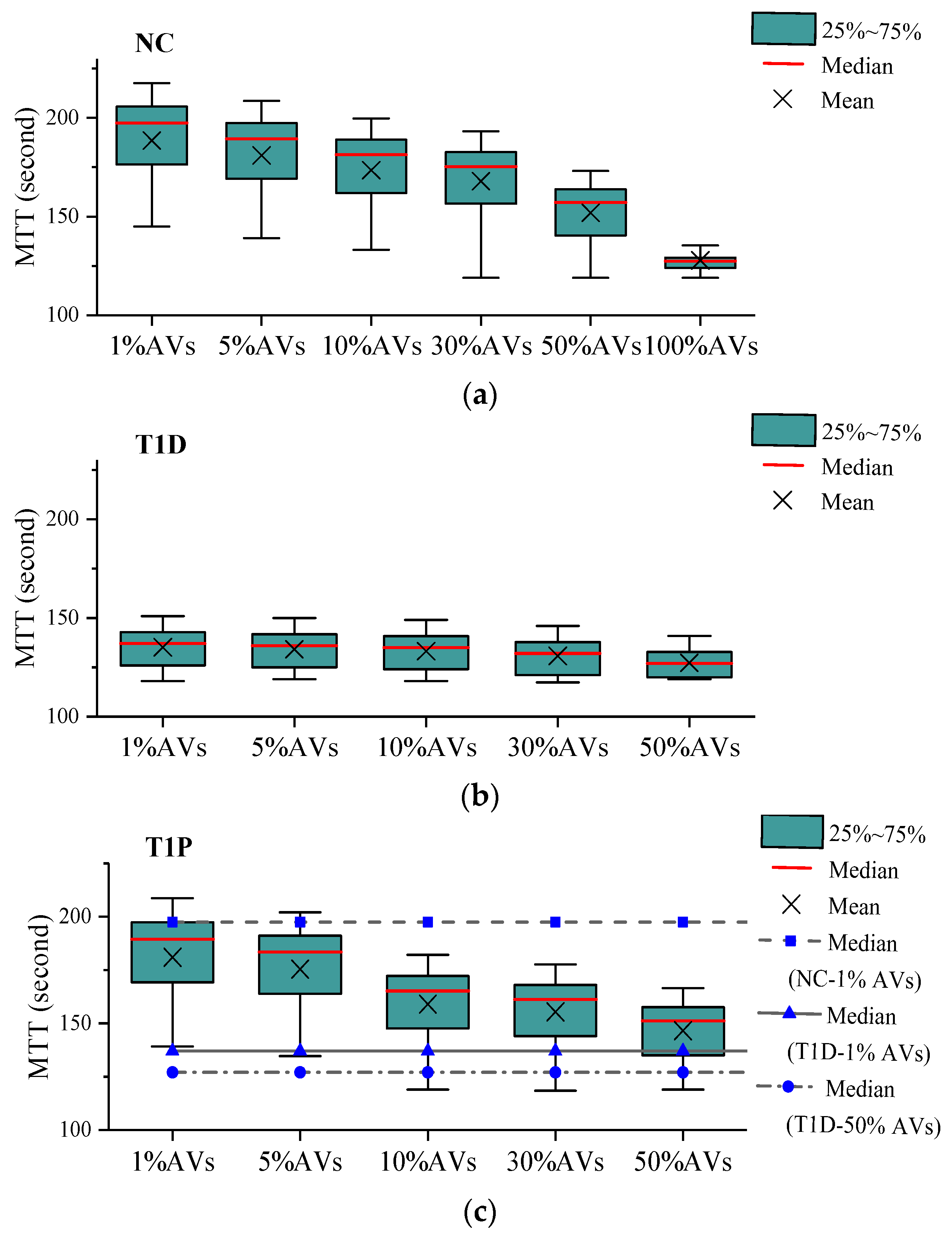
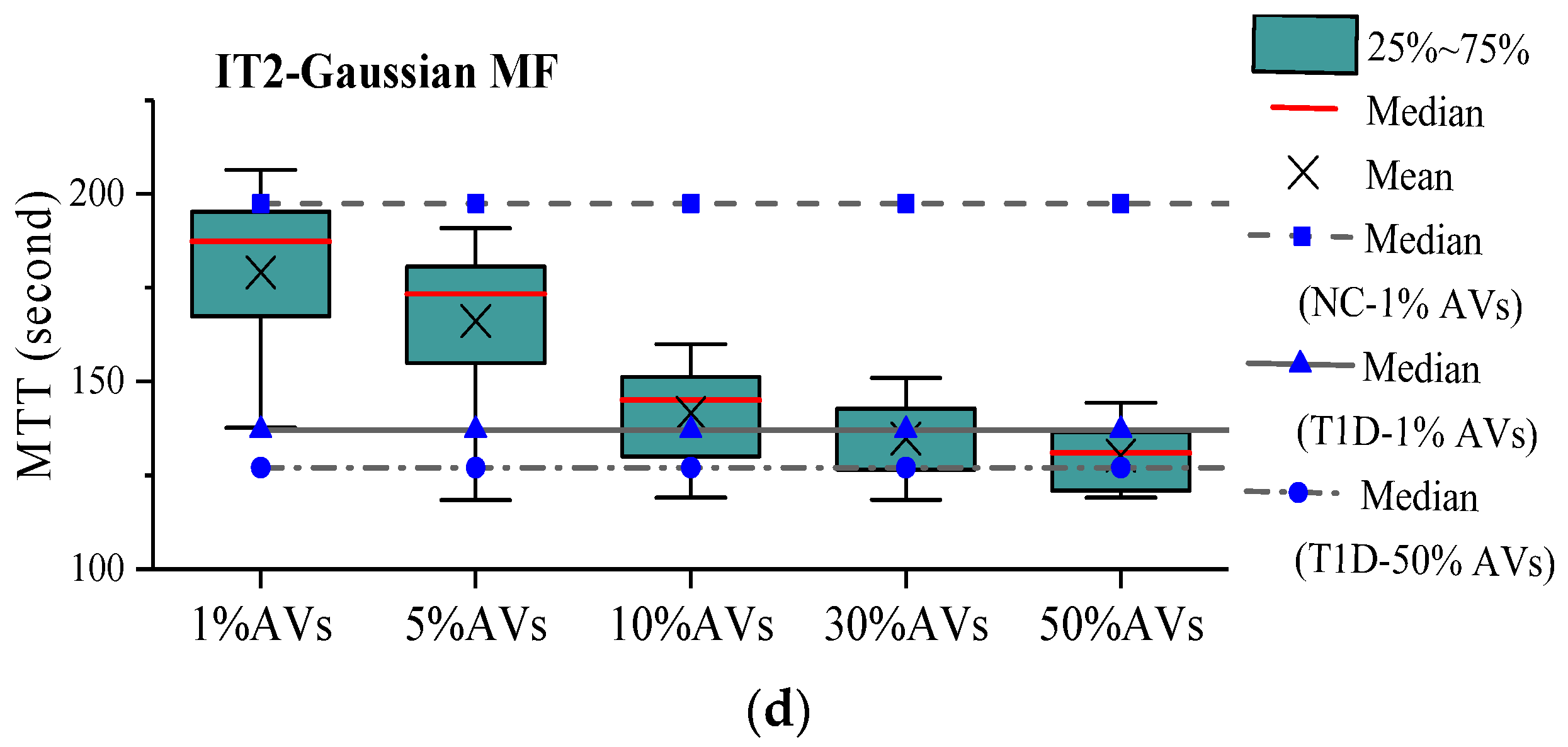
5. Analysis Results
- No Control (NC for short) scenario, which is used as a baseline to measure improvements offered by other control scenarios;
- T1-FLS based VSL with detector data (T1D for short) scenario in which speed limits are determined using T1-FLS and data directly collected from loop detectors;
- T1-FLS based VSL with PVD (T1P for short) scenario in which speed limits are determined using T1-FLS and data collected from PVs or CAVs; and
- IT2-FLS based VSL with PVD (IT2 for short) scenario in which speed limits are determined using the proposed IT2 FLS and data collected from PVs or CAVs.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fagnant, D.J.; Kockelman, K. Preparing a nation for autonomous vehicles: Opportunities, barriers and policy recommendations. Transp. Res. A Policy Pract. 2015, 77, 167–181. [Google Scholar] [CrossRef]
- Seo, T.; Bayen, A.M.; Kusakabe, T.; Asakura, Y. Traffic state estimation on highway: A comprehensive survey. Annu. Rev. Control 2017, 43, 128–151. [Google Scholar] [CrossRef] [Green Version]
- Bekiaris-Liberis, N.; Roncoli, C.; Papageorgiou, M. Highway Traffic State Estimation with Mixed Connected and Conventional Vehicles. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3484–3497. [Google Scholar] [CrossRef] [Green Version]
- Kattan, L.; Khondaker, B.; Derushkina, O.; Poosarla, E. A Probe-Based Variable Speed Limit System. Int. J. Intell. Transp. Syst. Res. 2015, 19, 339–354. [Google Scholar] [CrossRef]
- Yuan, Y.; Van Lint, H.; Van Wageningen-Kessels, F.; Hoogendoorn, S. Network-Wide Traffic State Estimation Using Loop Detector and Floating Car Data. Int. J. Intell. Transp. Syst. Res. 2014, 18, 41–50. [Google Scholar] [CrossRef]
- Herrera, J.C.; Work, D.B.; Herring, R.; Ban, X.; Jacobson, Q.; Bayen, A.M. Evaluation of traffic data obtained via GPS-enabled mobile phones: The Mobile Century field experiment. Transp. Res. C 2010, 18, 568–583. [Google Scholar] [CrossRef] [Green Version]
- Erdmann, J.; Oertel, R.; Wagner, P. VITAL: A simulation-based assessment of new traffic light controls. In Proceedings of the 18th International IEEE Conference on Intelligent Transportation Systems, Las Palmas, Spain, 15–18 September 2015. [Google Scholar]
- Oertel, R.; Wagner, P. Delay-Time Actuated Traffic Signal Control for an Isolated Intersection. In Proceedings of the 90st Annual Meeting Transportation Research Board, Washington, DC, USA, 23–27 January 2011. [Google Scholar]
- Habtemichael, F.; Picado-Santos, L. Safety and Operational Benefits of Variable Speed Limit Under Different Traffic Conditions and Driver Compliance Levels. In Proceedings of the 92nd Annual Meeting of Transportation Research Board, Washington, DC, USA, 13–17 January 2013. [Google Scholar]
- Elefteriadou, L.; Washburn, S.; Yin, Y.; Modi, Y.; Letter, C. Variable Speed Limit (VSL)–Best Management Practice. Available online: https://rosap.ntl.bts.gov/view/dot/24906 (accessed on 22 December 2019).
- Lee, C.; Hellinga, B.; Saccomanno, F. Assessing Safety Benefits of Variable Speed Limits. Transp. Res. Rec. 2004, 1897, 183–190. [Google Scholar] [CrossRef]
- Allaby, P.; Hellinga, B.; Bullock, M. Variable Speed Limits: Safety and Operational Impacts of a Candidate Control Strategy for Freeway Applications. IEEE Trans. Intell. Transp. Syst. 2007, 8, 671–680. [Google Scholar] [CrossRef]
- Li, D.; Ranjitkar, P. A fuzzy logic-based variable speed limit controller. J. Adv. Transp. 2015, 49, 913–927. [Google Scholar] [CrossRef]
- Hegyi, A.; Schutter, B.D.; Hellendoorn, H. Model Predictive Control for Optimal Coordination of Ramp Metering and Variable Speed Limits. Transp. Res. C 2005, 13, 185–209. [Google Scholar] [CrossRef] [Green Version]
- Carlson, R.C.; Papamichail, I.; Papageorgiou, M.; Messmer, A. Variable Speed Limits as a Mainline Metering Device for Freeways. In Proceedings of the 89th Annual Meeting of Transportation Research Board, Washington, DC, USA, 10–14 January 2010. [Google Scholar]
- Yu, R.; Abdel-Aty, M. An optimal variable speed limits system ameliorate traffic safety risk. Transp. Res. C 2014, 46, 235–246. [Google Scholar] [CrossRef]
- Khondaker, B.; Kattan, L. Variable speed limit: A microscopic analysis in a connected vehicle environment. Transp. Res. C 2015, 58, 146–159. [Google Scholar] [CrossRef] [Green Version]
- Shladover, S.; Su, D.; Lu, X. Impacts of cooperative adaptive cruise control on freeway traffic flow. In Proceedings of the 91st Annual Meeting of the Transportation Research Board, Washington, DC, USA, 22–26 January 2012. [Google Scholar]
- Greenshields, B.D. A study in highway capacity. Highway Res. Board 1935, 1935, 448–477. [Google Scholar]
- Underwood, R.T. Speed, Volume, and Density Relationship: Quality and Theory of Traffic Flow; Yale Bureau of Highway Traffic: University Park, PA, USA, 1961; pp. 141–188. [Google Scholar]
- Van Aerde, M. Single regime speed-flow-density relationship for congested and congested highways. In Proceedings of the 74th TRB Annual Conference, Washington, DC, USA, 12–16 January 1995. [Google Scholar]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-1. Inf. Sci. 1975, 8, 199–249. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R. Type-2 Fuzzy Sets Made Simple. IEEE Trans. Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Hisdal, E. The IF THEN ELSE statement and interval-valued fuzzy sets of higher type. Int. J. Man Mach. Stud. 1981, 15, 385–455. [Google Scholar] [CrossRef]
- Liang, Q.; Mendel, J.M. Interval type-2 fuzzy logic systems: Theory and design. IEEE Trans. Trans. Fuzzy Syst. 2000, 8, 535–550. [Google Scholar] [CrossRef] [Green Version]
- Krajzewicz, D.; Erdmann, J.; Behrisch, M.; Bieker, L. Recent Development and Applications of SUMO-Simulation of Urban Mobility. Int. J. Adv. Syst. Meas. 2012, 5, 128–138. [Google Scholar]
- Dowling, R.; Skabardonis, A.; Halkias, J.; McHale, G.; Zammit, G. Guidelines for Calibration of Micro-simulation Models: Framework and Applications. Transp. Res. Rec. 2004, 1876, 1–9. [Google Scholar] [CrossRef]
- Taskin, A.; Kumbasar, T. An open source Matlab/Simulink Toolbox for Interval Type-2 Fuzzy Logic Systems. In Proceedings of the IEEE Symposium Series on Computational Intelligence, Cape Town, South Africa, 7–10 December 2015. [Google Scholar]
- Acosta, A.F.; Espinosa, J.E.; Espinosa, J. TraCI4Matlab: Enabling the Integration of the SUMO Road Traffic Simulator and Matlab® Through a Software Re-engineering Process. In Modeling Mobility with Open Data; Springer: New York, NY, USA, 2015; pp. 155–170. [Google Scholar]
- Krauß, S. Microscopic Modeling of Traffic Flow: Investigation of Collision Free Vehicle Dynamics. Ph.D. Thesis, Universitat zu Koln, Koln, Germany, 1998. [Google Scholar]
- Wagner, I. Size of the Global Autonomous Car Market 2018-2030. Available online: https://www.statista.com/statistics/428692/projected-size-of-global-autonomous-vehicle-market-by-vehicle-type/ (accessed on 22 December 2019).
- Statista Research Department. Projected Market Penetration of Autonomous Vehicles (Including Cars, Trucks, and Pods) in the United Kingdom (UK) from 2015 to 2030, by Level of Automation. Available online: https://www.statista.com/statistics/431899/projected-uk-market-penetration-of-autonomous-vehicles/ (accessed on 22 December 2019).


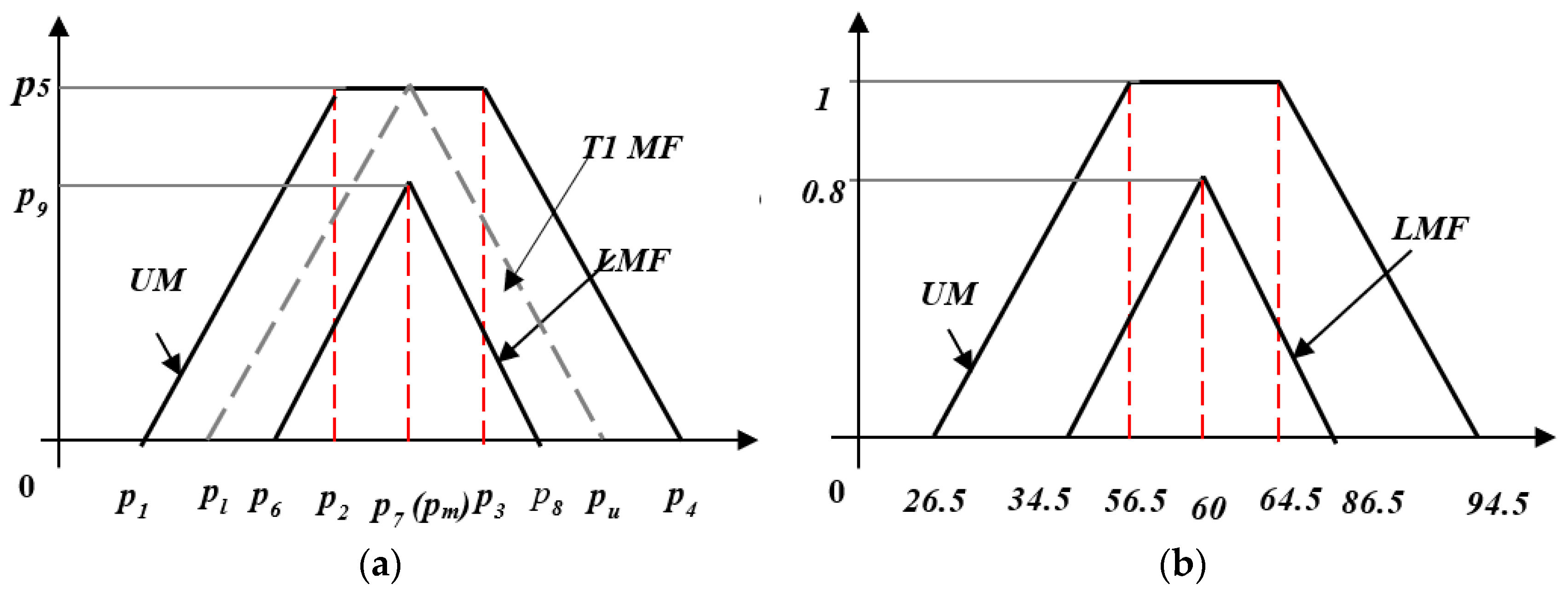
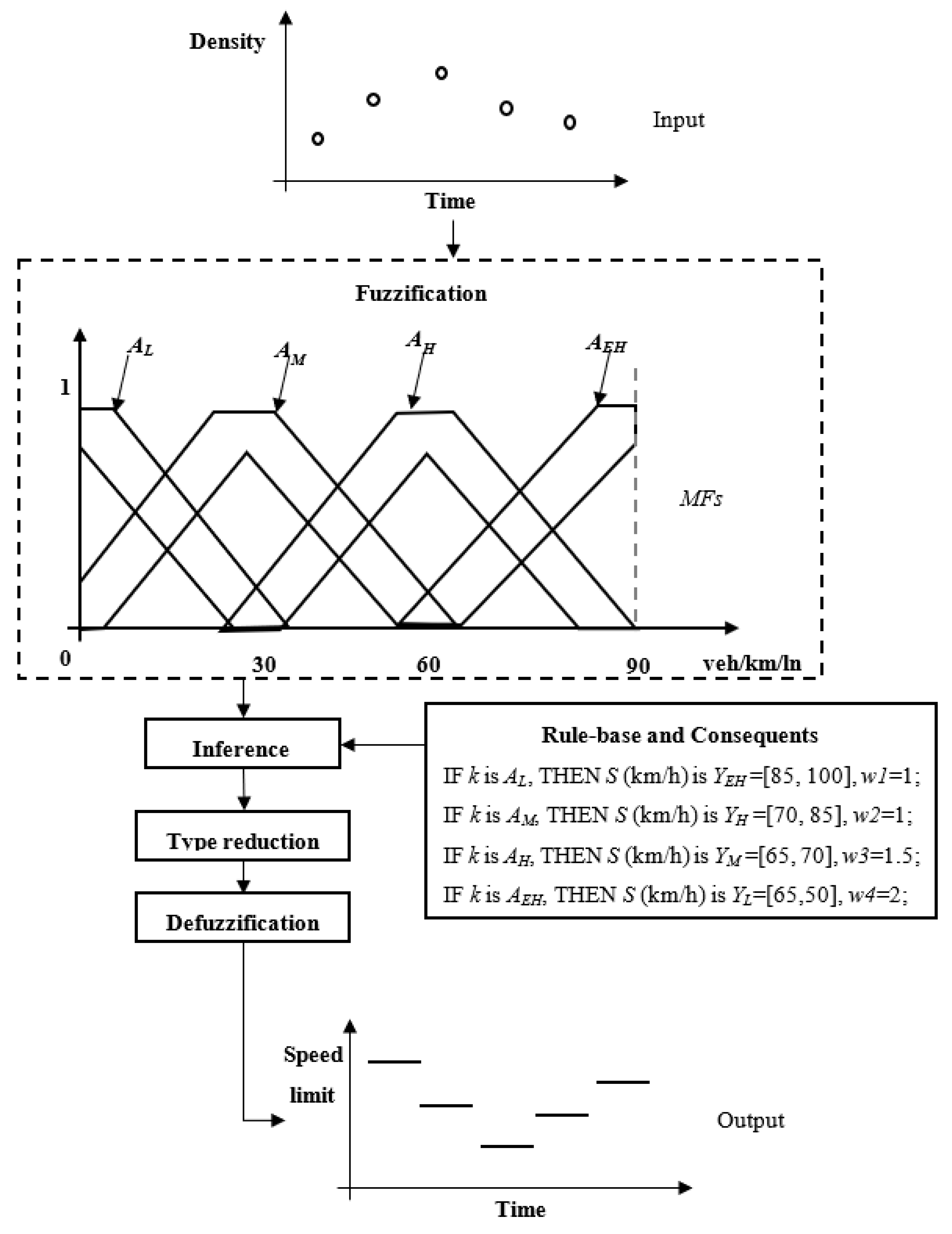


| No. | Weight | Premise | Consequent |
|---|---|---|---|
| 1 | w1 | IF density k is low (AL) | THEN speed limit S is extremely high (YEH), YEH = [ |
| 2 | w2 | IF density k is medium (AM) | THEN speed limit S is high (YH), YH = [ |
| 3 | w3 | IF density k is high (AH) | THEN speed limit S is medium (YM), YH = [ |
| 4 | w4 | IF density k is extremely high (AEH) | THEN speed limit S is low (YL), YH = [ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Wagner, P. A Novel Approach for Mixed Manual/Connected Automated Freeway Traffic Management. Sensors 2020, 20, 1757. https://doi.org/10.3390/s20061757
Li D, Wagner P. A Novel Approach for Mixed Manual/Connected Automated Freeway Traffic Management. Sensors. 2020; 20(6):1757. https://doi.org/10.3390/s20061757
Chicago/Turabian StyleLi, Duo, and Peter Wagner. 2020. "A Novel Approach for Mixed Manual/Connected Automated Freeway Traffic Management" Sensors 20, no. 6: 1757. https://doi.org/10.3390/s20061757
APA StyleLi, D., & Wagner, P. (2020). A Novel Approach for Mixed Manual/Connected Automated Freeway Traffic Management. Sensors, 20(6), 1757. https://doi.org/10.3390/s20061757





