A Fast Analysis Method for Blue-Green Laser Transmission through the Sea Surface
Abstract
:1. Introduction
2. Materials and Methods
2.1. Modeling Three-Dimensional Dynamic Wave
2.1.1. Wave Model
2.1.2. Normal Vector of the Sea Surface
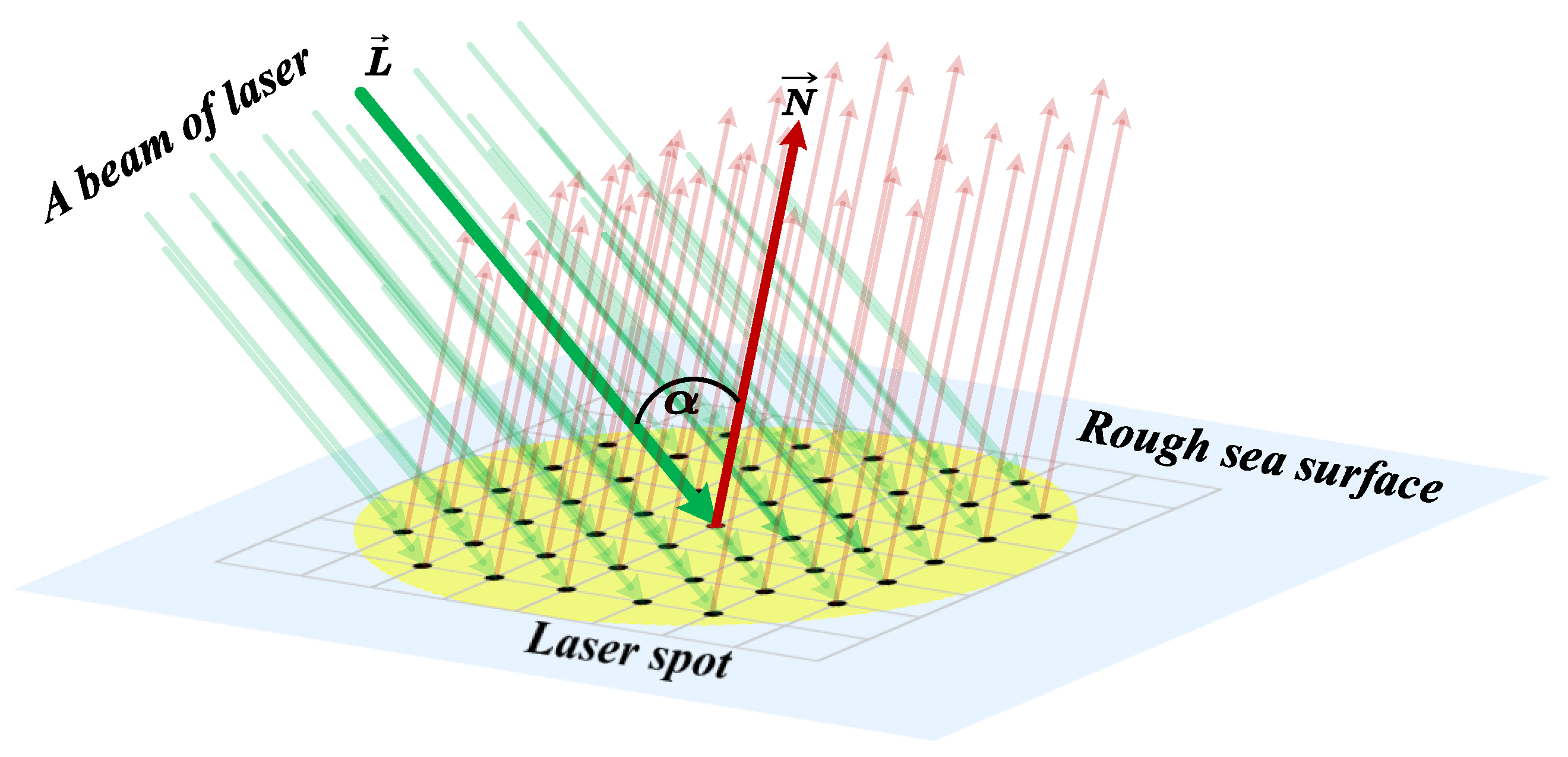
2.2. Modeling Transmittance at Different Incidence Angle
2.2.1. Incidence Angle Modeling
2.2.2. Transmittance Modeling
3. Simulations and Results
3.1. Simulation Conditions
3.2. Simulation Time
3.3. Statistics of Refraction Angles
3.4. Statistics of the Transmittance
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Collin, A.; Archambault, P.; Long, B. Mapping the Shallow Water Seabed Habitat with the SHOALS. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2947–2955. [Google Scholar] [CrossRef]
- Tulldahl, H.M.; Philipson, P.; Kautsky, H.; Wikstrom, S.A. Sea Floor Classification with Satellite Data and Airborne Lidar Bathymetry. In Ocean Sensing and Monitoring V.; Hou, W.W., Arnone, R.A., Eds.; Spie-Int Soc Optical Engineering: Bellingham, WA, USA, 2013; Volume 8724, p. UNSP 87240B. ISBN 978-0-8194-9515-0. [Google Scholar]
- Wang, M.; Yuan, X.; AlHarbi, O.; Deng, P.; Kane, T. Propagation of laser beams through air-sea turbulence channels. In Laser Communication and Propagation Through the Atmosphere and Oceans VII; Bos, J.P., VanEijk, A.M.J., Hammel, S.M., Eds.; Spie-Int Soc Optical Engineering: Bellingham, WA, USA, 2018; Volume 10770, p. UNSP 1077003. ISBN 978-1-5106-2112-1. [Google Scholar]
- Enqi, Z.; Hongyuan, W. Research on Spatial Spreading Effect of Blue-Green Laser Propagation through Seawater and Atmosphere; Ye, Z.W., Ma, P., Eds.; IEEE: New York, NY, USA, 2009; ISBN 978-1-4244-2909-7. [Google Scholar]
- Gordon, H.R.; Jacobs, M.M. Albedo of the ocean-atmosphere system: Influence of sea foam. Appl. Opt. 1977, 16, 2257–2260. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; Charlock, T.P.; Rutledge, K.; Stamnes, K.; Wang, Y. Analytical solution of radiative transfer in the coupled atmosphere-ocean system with a rough surface. Appl. Opt. 2006, 45, 7443–7455. [Google Scholar] [CrossRef] [PubMed]
- Tulldahl, H.M. Underwater irradiance fluctuations of a laser beam after transmission through a wavy sea surface. In Laser Applications in Medicine, Biology, and Environmental Science; International Society for Optics and Photonics: Moscow, Russian Federation, 2003; Volume 5149, pp. 251–258. [Google Scholar]
- Birkebak, M.; Eren, F.; Pe’eri, S.; Weston, N. The Effect of Surface Waves on Airborne Lidar Bathymetry (ALB) Measurement Uncertainties. Remote Sens. 2018, 10, 453. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Miao, X.; Qi, X.; Han, X. Research on the propagation characteristics of blue-green laser through sea surface with foams. Optik 2018, 170, 265–271. [Google Scholar] [CrossRef]
- Westfeld, P.; Maas, H.-G.; Richter, K.; Weiß, R. Analysis and correction of ocean wave pattern induced systematic coordinate errors in airborne LiDAR bathymetry. ISPRS J. Photogramm. Remote Sens. 2017, 128, 314–325. [Google Scholar] [CrossRef]
- Pierson, W.J.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of S. J. Geophys. Rese. Atmos. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Xiaolu, C.; Biao, C.; Ronghua, T.; Suqin, X. Three Dimensional Simulation of Ocean Surface Wave Based on Directional Spectrum; Amer Soc Mechanical Engineers: New York, NY, USA, 2012; ISBN 978-0-7918-5991-9. [Google Scholar]
- Qiu, Y.G.; Xu, Z.Y.; Ying, J.S. Three-Dimensional Ocean Wave Simulation Based on Directional Spectrum. Appl. Mech. Mater. 2011, 94–96, 2074–2079. [Google Scholar]
- Tessendorf, J. Simulating ocean water. In Simulating Nature: Realistic and Interactive Techniques; SIGGRAPH: Washington, DC, USA, 2001; Volume 1, p. 5. [Google Scholar]
- Cox, C.; Zhang, X. Optical methods for study of sea surface roughness and microscale turbulence. In Optical Technology in Fluid, Thermal, and Combustion Flow III; Cha, S.S., Trolinger, J.D., Kawahashi, M., Eds.; Spie-Int Soc Optical Engineering: Bellingham, WA, USA, 1997; Volume 3172, pp. 165–172. ISBN 978-0-8194-2594-2. [Google Scholar]
- Chun, H.; Suh, K.-D. Estimation of significant wave period from wave spectrum. Ocean Eng. 2018, 163, 609–616. [Google Scholar] [CrossRef]
- Li, J.; Zhou, L.; Li, S. Inversion of wave period in the North Pacific Ocean with TOPEX altimeter data. Mar. Sci. Bull. 2012, 30–39. [Google Scholar]
- Dongliang, Z.; Shuiqing, L.; Chaoyang, S. The comparison of altimeter retrieval algorithms of the wind speed and the wave period. Acta Oceanol. Sin. 2012, 31, 1–9. [Google Scholar]
- Dai, C.; Wang, X. Statistical characteristics of wind and wave surges in the coastal and adjacent waters of eastern China. In Yangtze River Delta Meteorological Science and Technology Forum 2010; Yangtze River Delta Meteorological Science and Technology Forum: Jiaxing, China, 2010; pp. 487–491. [Google Scholar]
- Yang, F.; Su, D.; Ma, Y.; Feng, C.; Yang, A.; Wang, M. Refraction correction of airborne LiDAR bathymetry based on sea surface profile and ray tracing. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6141–6149. [Google Scholar] [CrossRef]
- Dong, Y.; Li, C.; Huang, R. Monte Carlo simulation method of atmosphere-ocean laser transmission. In International Conference on Space Information Technology 2009; International Society for Optics and Photonics: Beijing, China, 2010; Volume 7651, p. 76510B. [Google Scholar]
- Horwood, J.M.K.; Thurley, R.W.F.; Belmont, M.R.; Baker, J. Shallow angle LIDAR for wave measurement. In Proceedings of the Europe Oceans 2005, Brest, France, 20–23 June 2005; Volume 2, pp. 1151–1154. [Google Scholar]
- Tian, W. On tidal tilt corrections to large ring laser gyroscope observations. Geophys. J. Int. 2014, 196, 189–193. [Google Scholar] [CrossRef] [Green Version]










| Wind Scale 1 | Wave Grade 1 | (m/s) | (rad/s) | (rad/s) | (rad/s) | (rad) | ||
|---|---|---|---|---|---|---|---|---|
| 3 | Micro waves | 5 | 1.71 | 1.2~5.0 | 0.2 | 20 | 7 | |
| 4 | Small waves | 7 | 1.22 | 0.6~4.0 | 0.2 | 18 | 11 | |
| 5 | Moderate waves | 9 | 0.95 | 0.5~2.5 | 0.1 | 21 | 11 | |
| 6 | Large waves | 13 | 0.66 | 0.4~2.0 | 0.1 | 17 | 11 | |
| 7 | Strong waves | 16 | 0.54 | 0.3~1.6 | 0.05 | 27 | 21 | |
| 8–9 | High waves | 20 | 0.43 | 0.2~1.2 | 0.05 | 21 | 21 |
| Central Processing Unit (CPU) | Random Access Memory (RAM) | Graphics Processing Unit (GPU) | Integrated Development Environment (IDE) | Parallel Pool |
|---|---|---|---|---|
| Intel(R) Core(TM) i7-7700 (3.60GHz) | 32 GB | NVIDIA GeForce GTX 1060 (6 GB) | Matlab R2016b | 4 cores |
| 500 | 20 | 0.5 | 300 | 55k | 10 |
| Wind Speed (m/s) | Wind Direction (deg) | Time of Differential Analytic Method (s) | Time of the Proposed Method (s) | Time Reduction Proportion |
|---|---|---|---|---|
| 5 | 0 | 25.72 | 8.46 | 67.11% |
| 5 | 45 | 21.02 | 6.83 | 67.51% |
| 5 | 90 | 13.86 | 3.89 | 71.94% |
| 5 | 135 | 11.42 | 3.33 | 70.84% |
| 5 | 180 | 16.06 | 4.39 | 72.67% |
| 7 | 0 | 16.11 | 4.80 | 70.21% |
| 7 | 45 | 21.25 | 6.27 | 70.49% |
| 7 | 90 | 26.68 | 8.64 | 67.61% |
| 7 | 135 | 21.58 | 6.95 | 67.80% |
| 7 | 180 | 17.50 | 4.38 | 74.98% |
| 9 | 0 | 11.79 | 3.49 | 70.40% |
| 9 | 45 | 14.57 | 4.49 | 69.18% |
| 9 | 90 | 15.96 | 4.89 | 69.35% |
| 9 | 135 | 21.68 | 6.68 | 69.19% |
| 9 | 180 | 34.24 | 9.23 | 73.04% |
| 13 | 0 | 26.58 | 7.64 | 71.26% |
| 13 | 45 | 14.94 | 4.06 | 72.82% |
| 13 | 90 | 11.09 | 3.66 | 67.00% |
| 13 | 135 | 16.95 | 4.95 | 70.79% |
| 13 | 180 | 18.26 | 5.70 | 68.79% |
| 16 | 0 | 24.88 | 6.91 | 72.23% |
| 16 | 45 | 34.63 | 10.13 | 70.75% |
| 16 | 90 | 31.12 | 8.39 | 73.04% |
| 16 | 135 | 12.82 | 4.09 | 68.09% |
| 16 | 180 | 11.96 | 3.81 | 68.16% |
| 20 | 0 | 18.14 | 4.83 | 73.37% |
| 20 | 45 | 20.34 | 5.38 | 73.55% |
| 20 | 90 | 22.62 | 7.32 | 67.64% |
| 20 | 135 | 40.72 | 10.96 | 73.09% |
| 20 | 180 | 31.35 | 8.69 | 72.28% |
| Wind Speed (m/s) | Wind Direction (deg) | Minimum (rad) | Maximum (rad) | Average (rad) |
|---|---|---|---|---|
| 5 | 0 | 0.1702 | 0.3451 | 0.2618 |
| 5 | 45 | 0.1656 | 0.3539 | 0.2631 |
| 5 | 90 | 0.2034 | 0.3512 | 0.2650 |
| 5 | 135 | 0.1884 | 0.3446 | 0.2629 |
| 5 | 180 | 0.1918 | 0.3585 | 0.2618 |
| 7 | 0 | 0.1405 | 0.3602 | 0.2633 |
| 7 | 45 | 0.1626 | 0.3848 | 0.2654 |
| 7 | 90 | 0.1768 | 0.3760 | 0.2680 |
| 7 | 135 | 0.1540 | 0.3816 | 0.2652 |
| 7 | 180 | 0.1864 | 0.3800 | 0.2632 |
| 9 | 0 | 0.1506 | 0.3613 | 0.2646 |
| 9 | 45 | 0.1529 | 0.3738 | 0.2657 |
| 9 | 90 | 0.1564 | 0.3722 | 0.2667 |
| 9 | 135 | 0.1597 | 0.3648 | 0.2657 |
| 9 | 180 | 0.1583 | 0.3657 | 0.2647 |
| 13 | 0 | 0.1878 | 0.3514 | 0.2639 |
| 13 | 45 | 0.1704 | 0.3649 | 0.2645 |
| 13 | 90 | 0.1759 | 0.3639 | 0.2652 |
| 13 | 135 | 0.1634 | 0.3609 | 0.2645 |
| 13 | 180 | 0.1931 | 0.3572 | 0.2646 |
| 16 | 0 | 0.1432 | 0.3448 | 0.2649 |
| 16 | 45 | 0.1582 | 0.3716 | 0.2647 |
| 16 | 90 | 0.1627 | 0.3576 | 0.2648 |
| 16 | 135 | 0.1774 | 0.3648 | 0.2650 |
| 16 | 180 | 0.1719 | 0.3668 | 0.2650 |
| 20 | 0 | 0.1805 | 0.3594 | 0.2630 |
| 20 | 45 | 0.1611 | 0.3655 | 0.2637 |
| 20 | 90 | 0.1580 | 0.3543 | 0.2644 |
| 20 | 135 | 0.1547 | 0.3537 | 0.2642 |
| 20 | 180 | 0.1535 | 0.3540 | 0.2647 |
| Wind Speed (m/s) | Wind Direction (deg) | Minimum | Maximum | Average |
|---|---|---|---|---|
| 5 | 0 | 0.95847 | 0.95952 | 0.95921 |
| 5 | 45 | 0.95831 | 0.95951 | 0.95921 |
| 5 | 90 | 0.95850 | 0.95952 | 0.95920 |
| 5 | 135 | 0.95760 | 0.95955 | 0.95916 |
| 5 | 180 | 0.95785 | 0.95956 | 0.95917 |
| 7 | 0 | 0.95849 | 0.95954 | 0.95920 |
| 7 | 45 | 0.95852 | 0.95956 | 0.95920 |
| 7 | 90 | 0.95803 | 0.95955 | 0.95920 |
| 7 | 135 | 0.95767 | 0.95955 | 0.95920 |
| 7 | 180 | 0.95829 | 0.95948 | 0.95920 |
| 9 | 0 | 0.95812 | 0.95951 | 0.95917 |
| 9 | 45 | 0.95789 | 0.95953 | 0.95918 |
| 9 | 90 | 0.95854 | 0.95953 | 0.95919 |
| 9 | 135 | 0.95838 | 0.95954 | 0.95920 |
| 9 | 180 | 0.95824 | 0.95952 | 0.95919 |
| 13 | 0 | 0.95813 | 0.95954 | 0.95920 |
| 13 | 45 | 0.95840 | 0.95951 | 0.95920 |
| 13 | 90 | 0.95819 | 0.95955 | 0.95917 |
| 13 | 135 | 0.95805 | 0.95956 | 0.95917 |
| 13 | 180 | 0.95830 | 0.95953 | 0.95919 |
| 16 | 0 | 0.95832 | 0.95953 | 0.95919 |
| 16 | 45 | 0.95832 | 0.95956 | 0.95919 |
| 16 | 90 | 0.95774 | 0.95953 | 0.95919 |
| 16 | 135 | 0.95816 | 0.95950 | 0.95922 |
| 16 | 180 | 0.95787 | 0.95952 | 0.95919 |
| 20 | 0 | 0.95836 | 0.95952 | 0.95919 |
| 20 | 45 | 0.95851 | 0.95950 | 0.95920 |
| 20 | 90 | 0.95817 | 0.95953 | 0.95919 |
| 20 | 135 | 0.95824 | 0.95956 | 0.95919 |
| 20 | 180 | 0.95807 | 0.95951 | 0.95920 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, L.; Li, N.; Xie, X.; Bao, C.; Li, X.; Li, D. A Fast Analysis Method for Blue-Green Laser Transmission through the Sea Surface. Sensors 2020, 20, 1758. https://doi.org/10.3390/s20061758
Dong L, Li N, Xie X, Bao C, Li X, Li D. A Fast Analysis Method for Blue-Green Laser Transmission through the Sea Surface. Sensors. 2020; 20(6):1758. https://doi.org/10.3390/s20061758
Chicago/Turabian StyleDong, Liwei, Ni Li, Xinhao Xie, Chenying Bao, Xiaolu Li, and Duan Li. 2020. "A Fast Analysis Method for Blue-Green Laser Transmission through the Sea Surface" Sensors 20, no. 6: 1758. https://doi.org/10.3390/s20061758
APA StyleDong, L., Li, N., Xie, X., Bao, C., Li, X., & Li, D. (2020). A Fast Analysis Method for Blue-Green Laser Transmission through the Sea Surface. Sensors, 20(6), 1758. https://doi.org/10.3390/s20061758





