Sensing and Modelling Mechanical Response in Large Deformation Indentation of Adherent Cell Using Atomic Force Microscopy
Abstract
:1. Introduction
2. Modelling Methods
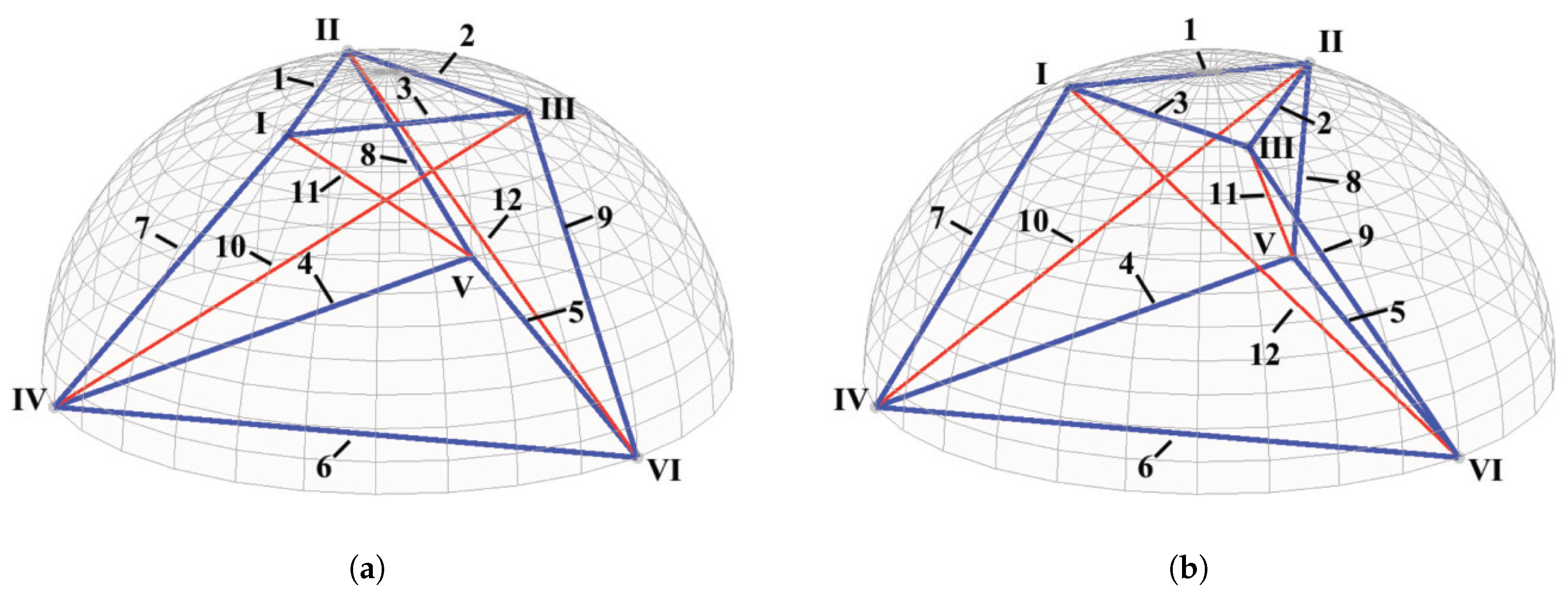
2.1. The Multi-Level Tensegrity Model
2.2. The Integrated Model
2.3. Central Indentation Simulation and the F-D Curve Similarity
2.4. Local Stiffness Analysis
3. Experimental Facilities and Methods
3.1. Cell Preparation
3.2. AFM System
3.3. Central Indentation
3.4. Data Process
4. Results
4.1. Mechanical Response of the Hyperelastic Components
4.2. Mechanical Responses of the Cytoskeletal Components
4.3. Evaluating the Models’ Accuracy
4.4. Local Stiffness Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lu, Z.; Moraes, C.; Ye, G.; Simmons, C.A.; Sun, Y. Single cell deposition and patterning with a robotic system. PLoS ONE 2010, 5, e13542. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xie, Y.; Sun, D.; Tse, H.Y.G.; Liu, C.; Cheng, S.H. Force sensing and manipulation strategy in robot-assisted microinjection on zebrafish embryos. IEEE/ASME Trans. Mechatron. 2011, 16, 1002–1010. [Google Scholar] [CrossRef]
- Karimirad, F.; Shirinzadeh, B.; Yan, W.; Fatikow, S. A vision-based methodology to dynamically track and describe cell deformation during cell micromanipulation. Int. J. Optomech. 2013, 7, 33–45. [Google Scholar] [CrossRef] [Green Version]
- Shirinzadeh, B.; Teoh, P.; Tian, Y.; Dalvand, M.; Zhong, Y.; Liaw, H. Laser interferometry-based guidance methodology for high precision positioning of mechanisms and robots. Robot. CIM-INT. Manuf. 2010, 26, 74–82. [Google Scholar] [CrossRef]
- Guo, Z.; Tian, Y.; Liu, C.; Wang, F.; Liu, X.; Shirinzadeh, B.; Zhang, D. Design and control methodology of a 3-DOF flexure-based mechanism for micro/nano-positioning. Robot. CIM-INT. Manuf. 2015, 32, 93–105. [Google Scholar] [CrossRef] [Green Version]
- Bhagat, U.; Shirinzadeh, B.; Clark, L.; Qin, Y.; Tian, Y.; Zhang, D. Experimental investigation of robust motion tracking control for a 2-DOF flexure-based mechanism. IEEE/ASME Trans. Mechatron. 2014, 19, 1737–1745. [Google Scholar] [CrossRef]
- Clark, L.; Shirinzadeh, B.; Tian, Y.; Yao, B. Development of a Passive Compliant Mechanism for Measurement of Micro/Nanoscale Planar 3-DOF Motions. IEEE/ASME Trans. Mechatron. 2016, 21, 1222–1232. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Y.; Shirinzadeh, B.; Smith, J.; Gu, C. Soft tissue deformation with reaction-diffusion process for surgery simulation. J. Visual. Lang. Comput. 2012, 23, 1–12. [Google Scholar] [CrossRef]
- Karimirad, F.; Chauhan, S.; Shirinzadeh, B. Vision-based force measurement using neural networks for biological cell microinjection. J. Biomech. 2014, 47, 1157–1163. [Google Scholar] [CrossRef]
- Zhao, Q.; Shirinzadeh, B.; Cui, M.; Sun, M.; Liu, Y.; Zhao, X. A novel cell weighing method based on the minimum immobilization pressure for biological applications. J. Appl. Phys. 2015, 118, 044301. [Google Scholar] [CrossRef]
- Becattini, G.; Mattos, L.S.; Caldwell, D.G. A fully automated system for adherent cells microinjection. IEEE J. Biomed. Health. Inform. 2014, 18, 83–93. [Google Scholar] [CrossRef] [PubMed]
- Radmacher, M. Measuring the elastic properties of biological samples with the AFM. IEEE Eng. Med. Biol. Mag. 1997, 16, 47–57. [Google Scholar] [CrossRef] [PubMed]
- Obataya, I.; Nakamura, C.; Han, S.; Nakamura, N.; Miyake, J. Mechanical sensing of the penetration of various nanoneedles into a living cell using atomic force microscopy. Biosens. Bioelectron. 2005, 20, 1652–1655. [Google Scholar] [CrossRef] [PubMed]
- Obataya, I.; Nakamura, C.; Han, S.; Nakamura, N.; Miyake, J. Nanoscale operation of a living cell using an atomic force microscope with a nanoneedle. Nano Lett. 2005, 5, 27–30. [Google Scholar] [CrossRef] [PubMed]
- Guillaume-Gentil, O.; Potthoff, E.; Ossola, D.; Franz, C.M.; Zambelli, T.; Vorholt, J.A. Force-controlled manipulation of single cells: From AFM to FluidFM. Trends Biotechnol. 2014, 32, 381–388. [Google Scholar] [CrossRef]
- Lin, D.C.; Dimitriadis, E.K.; Horkay, F. Robust strategies for automated AFM force curve analysis—I. Non-adhesive indentation of soft, inhomogeneous materials. J. Biomech. Eng. 2007, 129, 430–440. [Google Scholar] [CrossRef] [Green Version]
- Guo, Q.; Xia, Y.; Sandig, M.; Yang, J. Characterization of cell elasticity correlated with cell morphology by atomic force microscope. J. Biomech. 2012, 45, 304–309. [Google Scholar] [CrossRef]
- Krause, M.; te Riet, J.; Wolf, K. Probing the compressibility of tumor cell nuclei by combined atomic force–confocal microscopy. Phys. Biol. 2013, 10, 065002. [Google Scholar] [CrossRef]
- Zdunek, A.; Kurenda, A. Determination of the elastic properties of tomato fruit cells with an atomic force microscope. Sensors 2013, 13, 12175–12191. [Google Scholar] [CrossRef] [Green Version]
- Coceano, G.; Yousafzai, M.; Ma, W.; Ndoye, F.; Venturelli, L.; Hussain, I.; Bonin, S.; Niemela, J.; Scoles, G.; Cojoc, D.; et al. Investigation into local cell mechanics by atomic force microscopy mapping and optical tweezer vertical indentation. Nanotechnology 2015, 27, 065102. [Google Scholar] [CrossRef]
- Heuser, J.E.; Kirschner, M. Filament organization revealed in platinum replicas of freeze-dried cytoskeletons. J. Cell Biol. 1980, 86, 212–234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tan, Y.; Sun, D.; Huang, W.; Cheng, S.H. Characterizing mechanical properties of biological cells by microinjection. IEEE Trans. Nanobiosci. 2010, 9, 171–180. [Google Scholar] [CrossRef] [PubMed]
- Yoon, D.; You, D. Continuum modeling of deformation and aggregation of red blood cells. J. Biomech. 2016, 49, 2267–2279. [Google Scholar] [CrossRef] [PubMed]
- Shen, T.; Shirinzadeh, B.; Zhong, Y.; Smith, J. A hyperelastic model for mechanical responses of adherent cells in microinjection. Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO). In Proceedings of the 2017 IEEE International Conference, Shanghai, China, 7 August 2017; pp. 289–294. [Google Scholar]
- Bansod, Y.D.; Matsumoto, T.; Nagayama, K.; Bursa, J. A Finite Element Bendo-Tensegrity Model of Eukaryotic Cell. J. Biomech. Eng. 2018, 140, 101001. [Google Scholar] [CrossRef]
- Rusaczonek, M.; Zapotoczny, B.; Szymonski, M.; Konior, J. Application of a layered model for determination of the elasticity of biological systems. Micron 2019, 124, 102705. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Mollaeian, K.; Ren, J. Finite element modeling of living cells for AFM indentation-based biomechanical characterization. Micron 2019, 116, 108–115. [Google Scholar] [CrossRef] [PubMed]
- Florea, C.; Tanska, P.; Mononen, M.E.; Qu, C.; Lammi, M.J.; Laasanen, M.S.; Korhonen, R.K. A combined experimental atomic force microscopy-based nanoindentation and computational modeling approach to unravel the key contributors to the time-dependent mechanical behavior of single cells. Biomech. Model. Mechanobiol. 2017, 16, 297–311. [Google Scholar] [CrossRef] [PubMed]
- Ingber, D.E. Cellular tensegrity: Defining new rules of biological design that govern the cytoskeleton. J. Cell Sci. 1993, 104, 613–627. [Google Scholar]
- Kraning-Rush, C.M.; Carey, S.P.; Califano, J.P.; Smith, B.N.; Reinhart-King, C.A. The role of the cytoskeleton in cellular force generation in 2D and 3D environments. Phys. Biol. 2011, 8, 015009. [Google Scholar] [CrossRef] [Green Version]
- Gittes, F.; Mickey, B.; Nettleton, J.; Howard, J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 1993, 120, 923–934. [Google Scholar] [CrossRef]
- Deguchi, S.; Ohashi, T.; Sato, M. Evaluation of tension in actin bundle of endothelial cells based on preexisting strain and tensile properties measurements. MCB-TECH SCIENCE PRESS 2005, 2, 125. [Google Scholar]
- Ingber, D.E.; Wang, N.; Stamenović, D. Tensegrity, cellular biophysics, and the mechanics of living systems. Rep. Prog. Phys. 2014, 77, 046603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, J.X.; Janmey, P.A. The polyelectrolyte nature of F-actin and the mechanism of actin bundle formation. J. Biol. Chem. 1996, 271, 8556–8563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stamenović, D.; Fredberg, J.J.; Wang, N.; Butler, J.P.; Ingber, D.E. A microstructural approach to cytoskeletal mechanics based on tensegrity. J. Theor. Biol. 1996, 181, 125–136. [Google Scholar] [CrossRef] [PubMed]
- Ingber, D.E. Tensegrity I. Cell structure and hierarchical systems biology. J. Cell Sci. 2003, 116, 1157–1173. [Google Scholar] [CrossRef] [Green Version]
- Barreto, S.; Clausen, C.H.; Perrault, C.M.; Fletcher, D.A.; Lacroix, D. A multi-structural single cell model of force-induced interactions of cytoskeletal components. Biomaterials 2013, 34, 6119–6126. [Google Scholar] [CrossRef] [Green Version]
- Soheilypour, M.; Peyro, M.; Peter, S.J.; Mofrad, M.R. Buckling behavior of individual and bundled microtubules. Biophys. J. 2015, 108, 1718–1726. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Ohsaki, M. Adaptive force density method for form-finding problem of tensegrity structures. Int. J. Solids Struct. 2006, 43, 5658–5673. [Google Scholar] [CrossRef] [Green Version]
- Lin, D.C.; Dimitriadis, E.K.; Horkay, F. Robust strategies for automated AFM force curve analysis—II. adhesion-influenced indentation of soft, elastic materials. J. Biomech. Eng. 2007, 129, 904–912. [Google Scholar] [CrossRef] [Green Version]
- Potthoff, E.; Guillaume-Gentil, O.; Ossola, D.; Polesel-Maris, J.; LeibundGut-Landmann, S.; Zambelli, T.; Vorholt, J.A. Rapid and serial quantification of adhesion forces of yeast and mammalian cells. PLoS ONE 2012, 7, e52712. [Google Scholar] [CrossRef] [Green Version]
- Zhou, D.W.; García, A.J. Measurement systems for cell adhesive forces. J. Biomech. Eng. 2015, 137, 020908. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiang, H.; Zhang, J. Mechanics of microtubule buckling supported by cytoplasm. J. Appl. Mech. 2008, 75. [Google Scholar] [CrossRef] [Green Version]
- Peter, S.J.; Mofrad, M.R. Computational modeling of axonal microtubule bundles under tension. Biophys. J. 2012, 102, 749–757. [Google Scholar] [CrossRef] [PubMed] [Green Version]












| Component | Young’s Modulus (Pa) | Poisson’s Ratio | Diameter (nm) |
|---|---|---|---|
| Actin filiaments bundle [25] | 0.3 | 200 | |
| Microtubule [38] | 0.3 | (outer/inner) 23/17 |
| Level No. | AFB 1∼3 | AFB 4∼6 | AFB 7∼9 | MT 10∼12 |
|---|---|---|---|---|
| 1 | 17.20 | 17.32 | 5.21 | 19.26 |
| 2 | 16.67 | 17.32 | 5.28 | 19.00 |
| 3 | 15.80 | 17.32 | 5.43 | 18.59 |
| 4 | 14.61 | 17.32 | 5.69 | 18.02 |
| 5 | 13.12 | 17.32 | 6.07 | 17.30 |
| 6 | 11.37 | 17.32 | 6.61 | 16.46 |
| 7 | 9.38 | 17.32 | 7.30 | 15.52 |
| 8 | 7.21 | 17.32 | 8.12 | 14.49 |
| 9 | 4.88 | 17.32 | 9.06 | 13.41 |
| 10 | 2.46 | 17.32 | 10.09 | 12.29 |
| Level No. | AFB 1∼3 | AFB 4∼6 | AFB 7∼9 | MT 10∼12 |
|---|---|---|---|---|
| 1 | 1.00% | 0.99% | 0.50% | −8.73% |
| 2 | 1.00% | 0.96% | 0.53% | −8.64% |
| 3 | 1.00% | 0.91% | 0.54% | −8.45% |
| 4 | 1.00% | 0.84% | 0.57% | −8.20% |
| 5 | 1.00% | 0.76% | 0.61% | −7.82% |
| 6 | 1.00% | 0.66% | 0.70% | −7.44% |
| 7 | 1.00% | 0.54% | 0.73% | −7.05% |
| 8 | 1.00% | 0.42% | 0.81% | −6.58% |
| 9 | 1.00% | 0.28% | 0.91% | −6.10% |
| 10 | 1.00% | 0.14% | 1.01% | −5.57% |
| Components | Shear Modulus (Pa) |
|---|---|
| Membrane [22] | |
| Cytoplasm [25] | |
| Nucleus [25] |
| Property | Hyperelastic | Tensegrity | Integrated |
|---|---|---|---|
| (MPa) | / | ||
| (MPa) | / | 0.34 | |
| (MPa) | / | 50.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, T.; Shirinzadeh, B.; Zhong, Y.; Smith, J.; Pinskier, J.; Ghafarian, M. Sensing and Modelling Mechanical Response in Large Deformation Indentation of Adherent Cell Using Atomic Force Microscopy. Sensors 2020, 20, 1764. https://doi.org/10.3390/s20061764
Shen T, Shirinzadeh B, Zhong Y, Smith J, Pinskier J, Ghafarian M. Sensing and Modelling Mechanical Response in Large Deformation Indentation of Adherent Cell Using Atomic Force Microscopy. Sensors. 2020; 20(6):1764. https://doi.org/10.3390/s20061764
Chicago/Turabian StyleShen, Tianyao, Bijan Shirinzadeh, Yongmin Zhong, Julian Smith, Joshua Pinskier, and Mohammadali Ghafarian. 2020. "Sensing and Modelling Mechanical Response in Large Deformation Indentation of Adherent Cell Using Atomic Force Microscopy" Sensors 20, no. 6: 1764. https://doi.org/10.3390/s20061764





