Analysis and Compensation of Bias Drift for a Micromachined Spinning-Rotor Gyroscope with Electrostatic Suspension
Abstract
:1. Introduction
2. Device Description
2.1. Device Structure
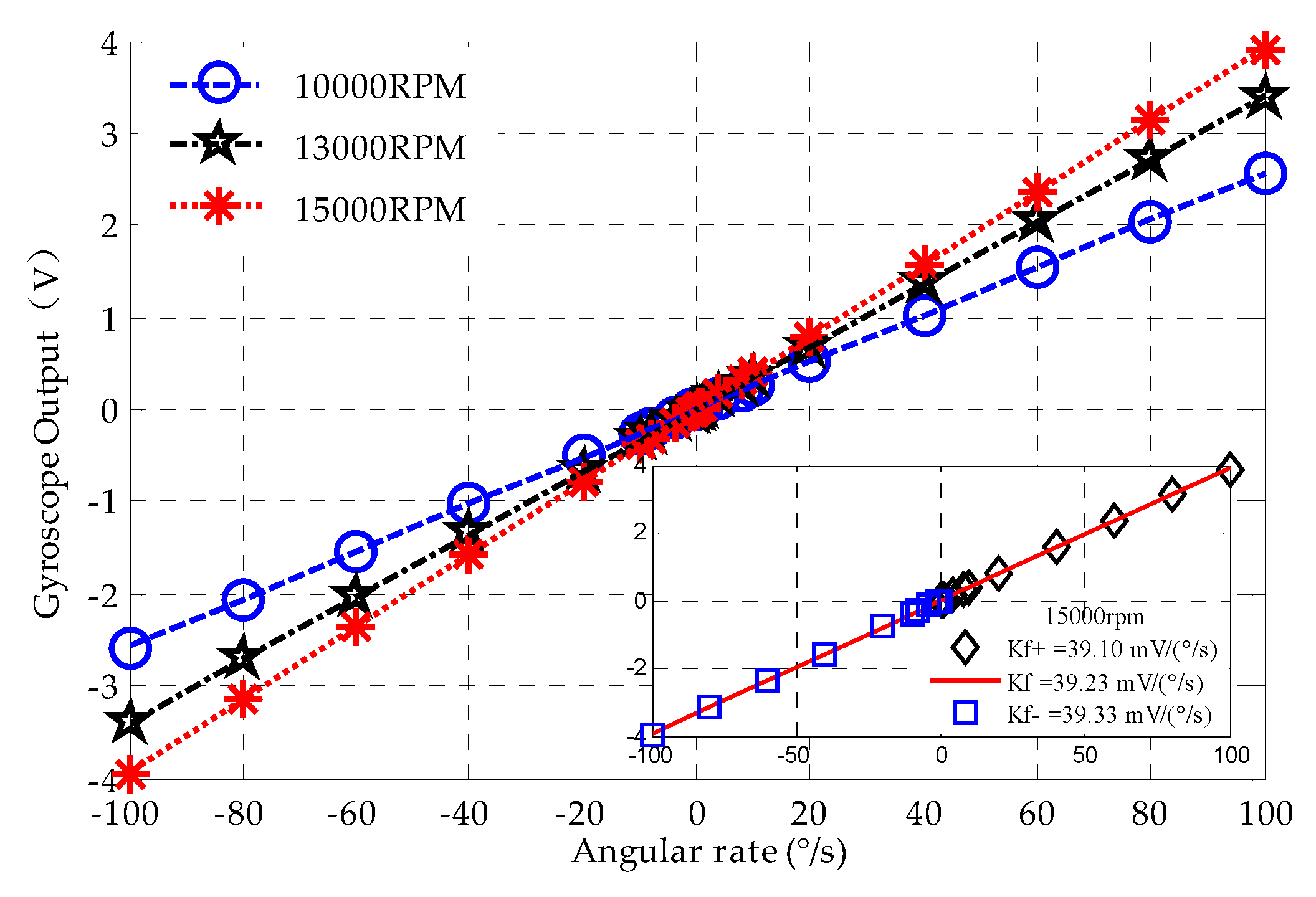
2.2. Scale Factor and Full-Scale Range
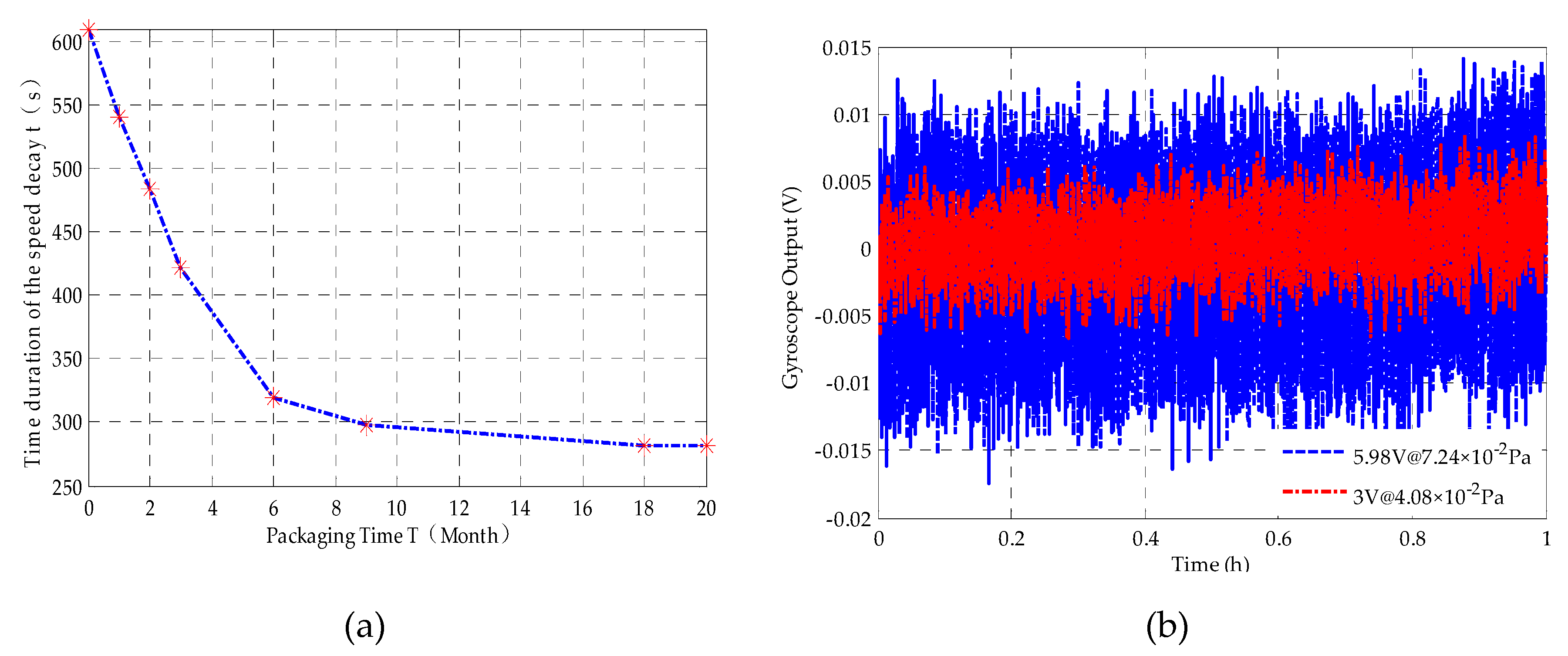
2.3. Vacuum Packaging
3. Temperature Dependent Characteristics of the MESG
3.1. Rotor Deformation-Induced Bias Drift
3.1.1. Theoretical Analysis of the Rotor Thermal’s Deformation
3.1.2. Bias Drift Caused by Thermal Expansion of the Rotor Structure
3.2. Radiative Thermal Transfer Model of the MESG
3.3. Temperature Drift Analysis of the Position Sensing Circuit
3.4. Gyroscopic Output Drift Caused by the Temperature Drift of Position Sensing Circuit
4. Experimental Results and Bias Drift Compensation
4.1. Experimental Set-Up for the MESG
4.2. Scale Factor
4.3. Bias Drift
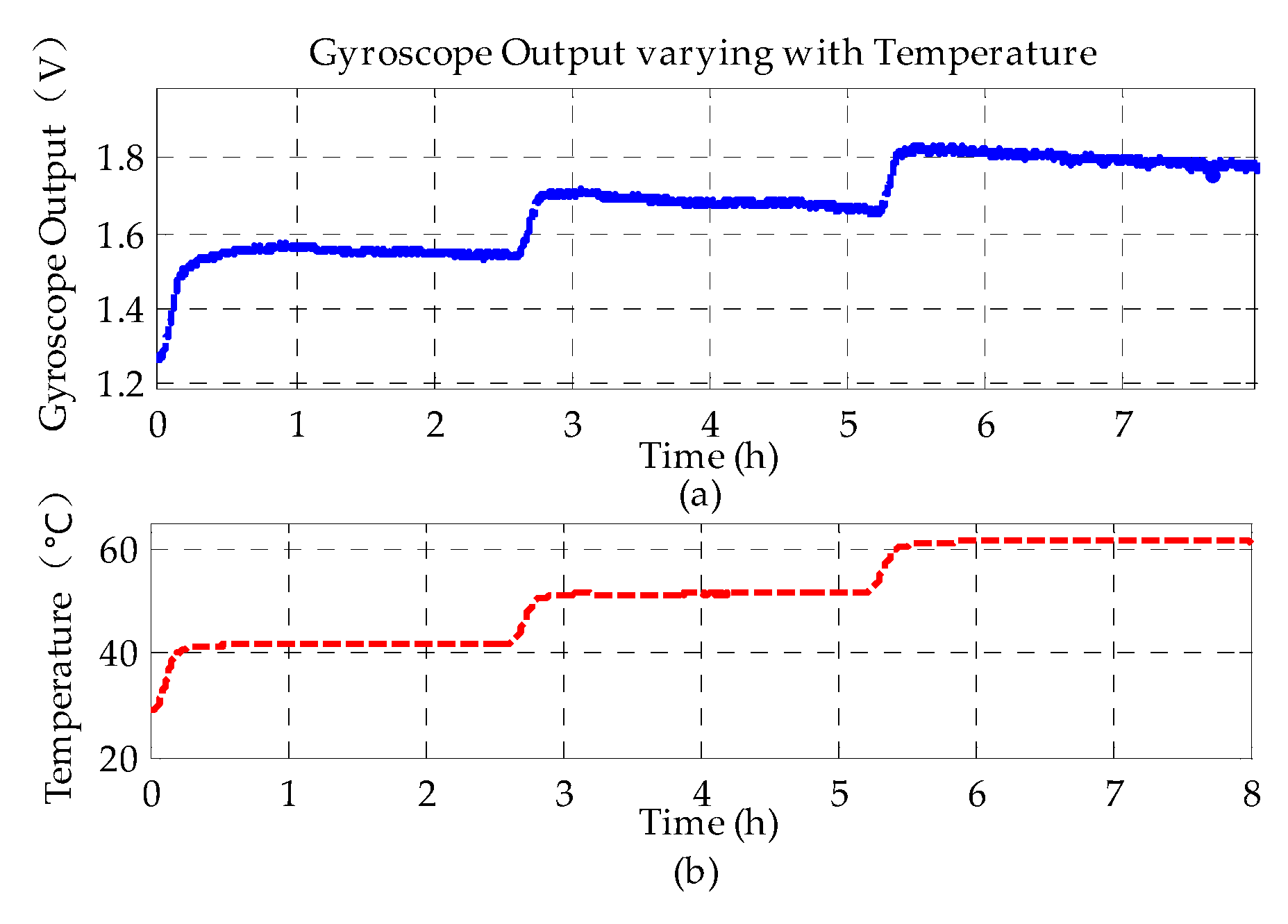
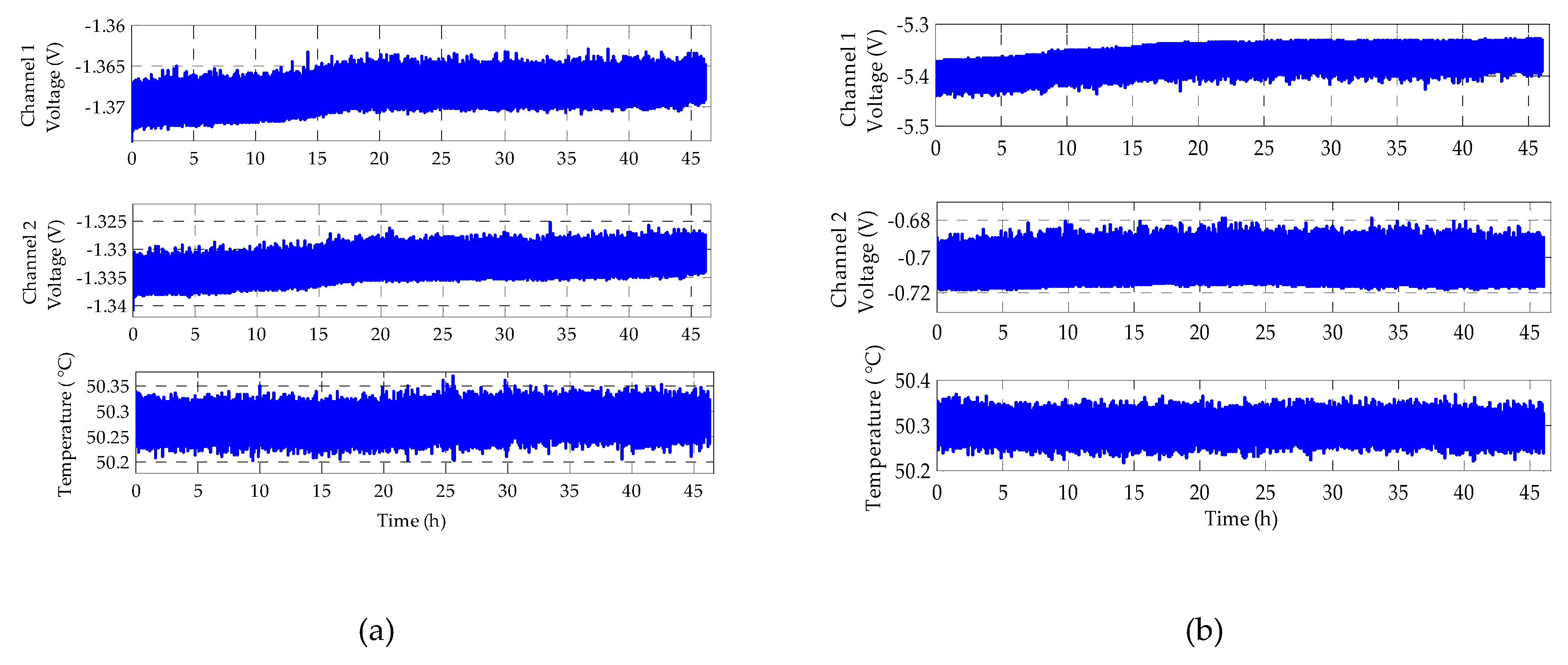
4.3.1. Temperature-Dependent Bias Drift
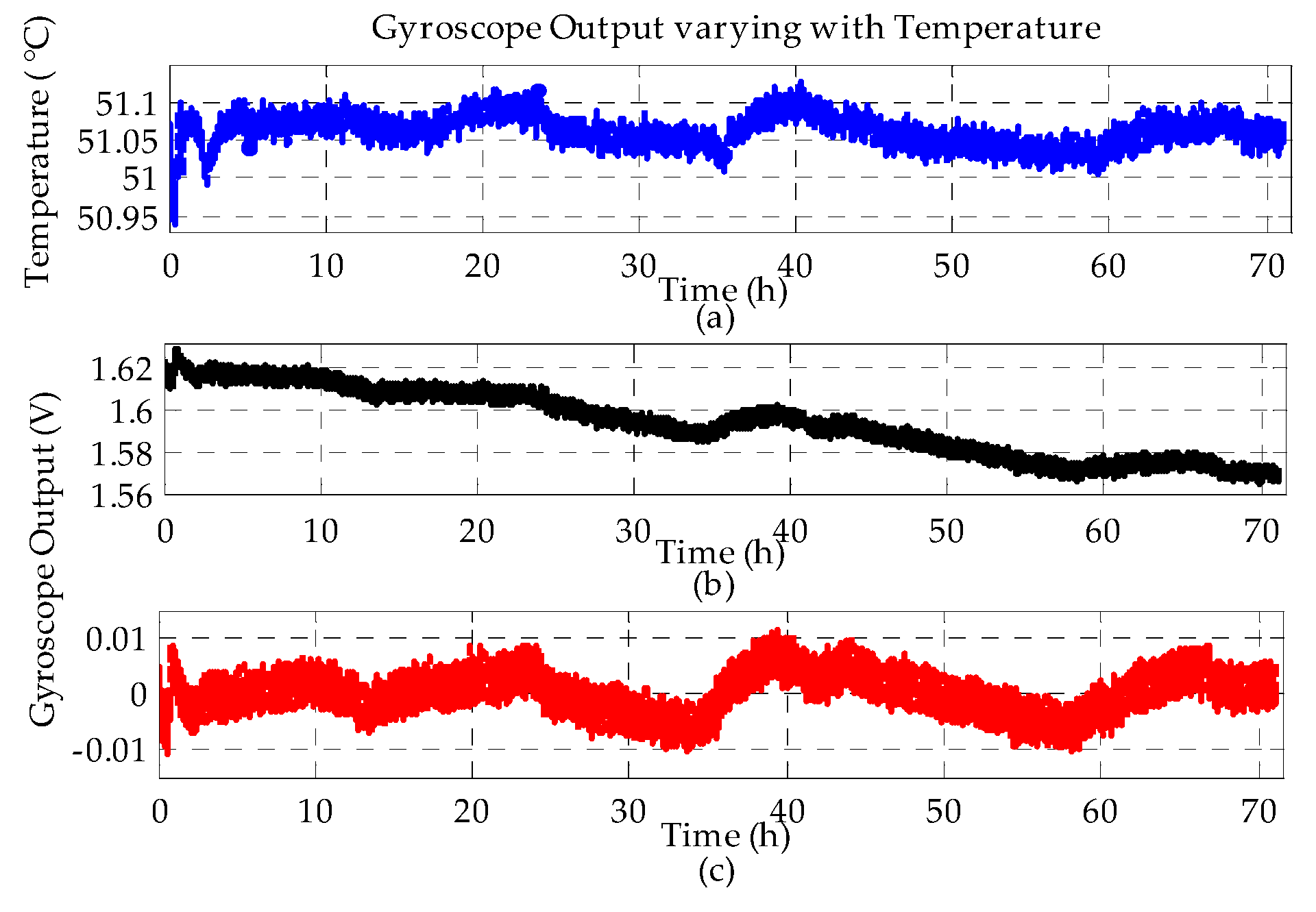
4.3.2. Long-Term Bias Stability of the MESG
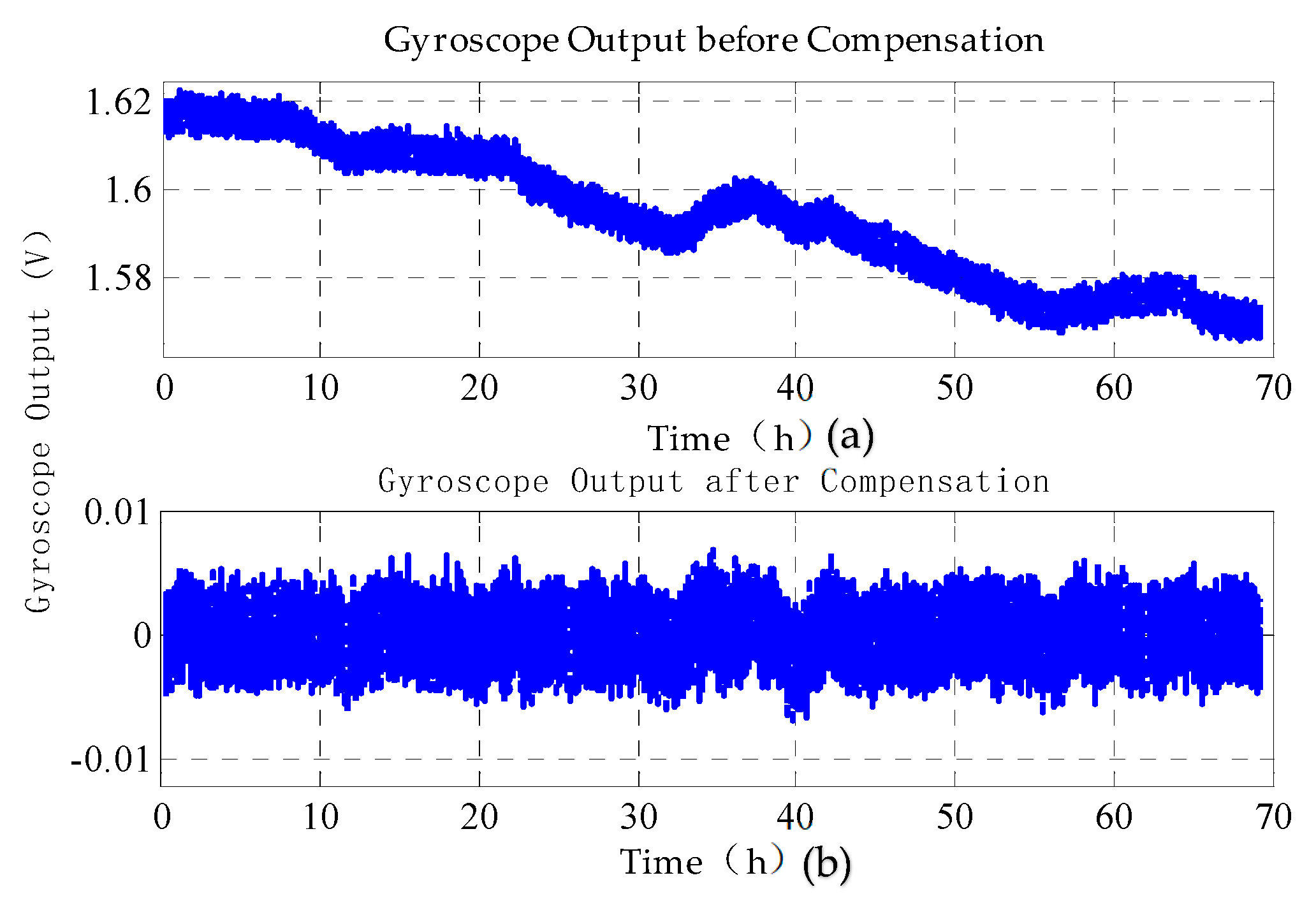
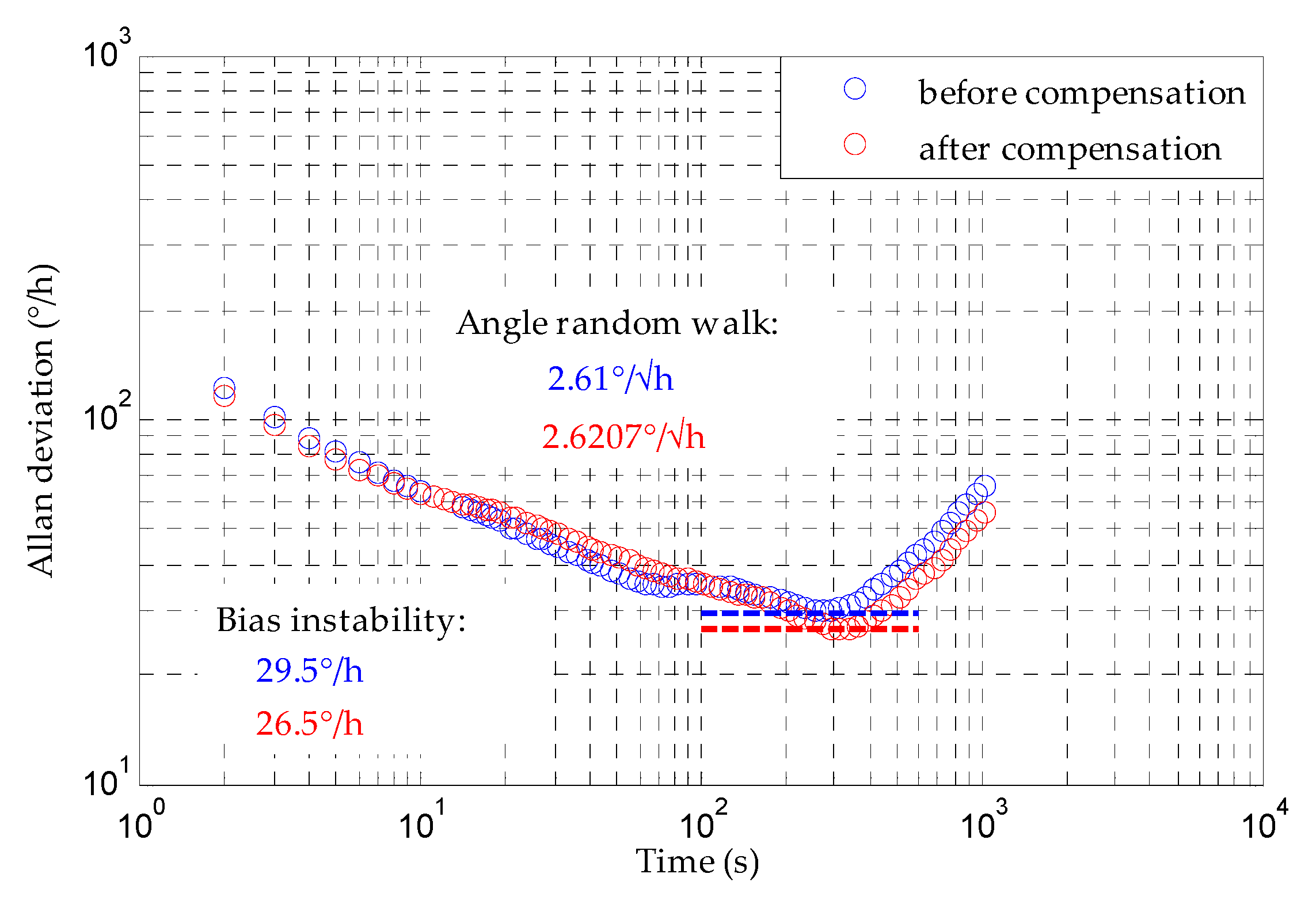
4.4. Compensation of Bias Drift Using a BP Neural Network
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xia, D.; Yu, C.; Kong, L. The Development of Micromachined Gyroscope Structure and Circuitry Technology. Sensors 2014, 14, 1394–1473. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yazdi, N.; Ayazi, F.; Najafi, K. Micromachined Inertial Sensors. Proc. IEEE 1998, 86, 1640–1659. [Google Scholar] [CrossRef] [Green Version]
- Wong, C.; Zhang, X.; Jacobson, S. A self-acting gas thrust bearing for high-speed microrotors. J. Microelectromech. Syst. 2004, 13, 158–164. [Google Scholar] [CrossRef]
- Chan, M.; Yoxall, B.; Park, H. Design and characterization of MEMS micromotor supported on low friction liquid bearing. Sens. Actuators A Phys. 2012, 177, 1–9. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, N.; Liu, X. Optimised geometry model for liquid-suspended miniature gyroscope. Micro Nano Lett. 2014, 9, 548–551. [Google Scholar] [CrossRef]
- Chen, D.; Liu, X.; Zhang, H. A rotational gyroscope with a water-film bearing based on magnetic self-restoring effect. Sensors 2018, 18, 415. [Google Scholar] [CrossRef] [Green Version]
- Han, F.; Wang, L.; Wu, Q. Performance of an active electric bearing for rotary micromotors. J. Micromech. Microeng. 2011, 21, 085027. [Google Scholar] [CrossRef]
- Sun, B.; Wang, S.; Tan, Y. Spin Rate Effects in a Micromachined Electrostatically Suspended Gyroscope. Sensors 2018, 18, 3901. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Chen, W.; Zhao, X. The study of an electromagnetic levitating micromotor for application in a rotating gyroscope. Sens. Actuators A Phys. 2006, 132, 651–657. [Google Scholar] [CrossRef]
- Esashi, M. Micro/nano electro mechanical systems for practical applications. J. Phys. Conf. Ser. 2009, 187, 012001. [Google Scholar] [CrossRef]
- Damrongsak, B.; Kraft, M.; Rajgopal, S. Design and fabrication of a micromachined electrostatically suspended gyroscope. Pro. Inst. Mech. Eng Part C J. Micromech. Microeng Sci. 2008, 222, 53–63. [Google Scholar] [CrossRef] [Green Version]
- Kraft, M.; Damrongsak, B. Micromachined gyroscopes based on a rotating mechanically unconstrained proof mass. In Proceedings of the SENSORS, 2010 IEEE, Kona, HI, USA, 1–4 November 2010; pp. 23–28. [Google Scholar]
- Poletkin, K.; Wallrabe, U. Static behavior of closed-loop micromachined levitated two-axis rate gyroscope. IEEE Sens. J. 2015, 15, 7001–7008. [Google Scholar] [CrossRef]
- Han, F.; Liu, Y.; Wang, L. Micromachined electrostatically suspended gyroscope with a spinning ring-shaped rotor. J. Micromech. Microeng. 2012, 22, 105032. [Google Scholar] [CrossRef]
- Sun, B.; Wang, S.; Tan, Y. High-yield triple-stack bonding fabrication process for micromachined micromotors with contactless rotor. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 1627–1630. [Google Scholar]
- Sun, B.; Han, F.; Li, L. Rotation control and characterization of high-speed variable-capacitance micromotor supported on electrostatic bearing. IEEE Trans. Ind. Electron. 2016, 63, 4336–4345. [Google Scholar] [CrossRef]
- Xu, G.; Tian, W.; Jin, Z. Temperature drift modelling and compensation for a dynamically tuned gyroscope by combining WT and SVM method. Meas. Sci. Technol. 2007, 18, 1425–1432. [Google Scholar] [CrossRef]
- Zotov, S.; Simon, B.; Sharma, G. Utilization of mechanical quadrature in silicon MEMS vibratory gyroscope to increase and expand the long term in-run bias stability. In Proceedings of the 2014 International Symposium on Inertial Sensors and Systems (ISISS), Laguna Beach, CA, USA, 25–26 February 2014; pp. 1–4. [Google Scholar]
- Chen, X.; Shen, C. Study on temperature error processing technique for fiber optic gyroscope. Optik 2013, 124, 784–792. [Google Scholar] [CrossRef]
- Challoner, A.; Howard, H.; Liu, J. Boeing disc resonator gyroscope. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium—PLANS 2014, Monterey, CA, USA, 5–8 May 2014; pp. 504–514. [Google Scholar]
- Fang, J.; Li, J. Integrated model and compensation of thermal errors of silicon microelectromechanical gyroscope. IEEE Trans. Instrum. Meas. 2009, 58, 2923–2930. [Google Scholar] [CrossRef]
- Liu, R.; El-Wailly, T.; Dankwort, R. Test results of Honeywell’s first-generation high-performance interferometric fiber optic gyroscope. Fiber Opt. Gyros Anniv. Conf. Int. Soc. Opt. Photonics 1992, 1585, 262–275. [Google Scholar]
- Prikhodko, I.; Trusov, A.; Shkel, A. Compensation of drifts in high-Q MEMS gyroscopes using temperature self-sensing. Sens. Actuators A Phys. 2013, 201, 517–524. [Google Scholar] [CrossRef] [Green Version]
- Shiau, J.; Huang, C.; Chang, M. Noise characteristics of MEMS gyro’s null drift and temperature compensation. J. Appl. Sci. Eng. 2012, 15, 239–246. [Google Scholar]
- Prikhodko, I.; Nadig, S.; Gregory, J. Half-a-month stable 0.2 degree-per-hour mode-matched MEMS gyroscope. In Proceedings of the 2017 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Kauai, HI, USA, 27–30 March 2017; pp. 1–4. [Google Scholar]
- Fukuda, G.; Hayashi, S. Inertial Navigation System with MEMS-ESG and Automated Sun Altitude Measuring System using Web-Camera. 2008, pp. 1–7. Available online: http://nornav.custompublish.com/getfile.php/1067052.753.ucpdyrysed/P%2014.pdf (accessed on 23 March 2020).
- Wang, S.; Han, F.; Sun, B. Squeeze-Film Air Damping of a Five-Axis Electrostatic Bearing for Rotary Micromotors. Sensors 2017, 17, 1119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Choa, S. Reliability of MEMS packaging: Vacuum maintenance and packaging induced stress. Microsyst. Technol. 2005, 11, 1187–1196. [Google Scholar] [CrossRef]
- Mahmood, A.; Butler, D.; Celik-Butler, Z. A device-level vacuum-packaging scheme for microbolometers on rigid and flexible substrates. IEEE Sens. J. 2007, 7, 1012–1019. [Google Scholar] [CrossRef] [Green Version]
- Chiao, M.; Lin, L. Device-level hermetic packaging of microresonators by RTP aluminum-to-nitride bonding. J. Microelectromech. Syst. 2006, 15, 515–522. [Google Scholar] [CrossRef]
- Zhang, Q.; Tan, Z.; Guo, L. Compensation of temperature drift of MEMS gyroscope using BP neural network. In Proceedings of the 2009 International Conference on Information Engineering and Computer Science, Wuhan, China, 19–20 December 2009; pp. 1–4. [Google Scholar]









| Description | Value |
|---|---|
| Rotor outer radius r0 (μm) | 2000 |
| Rotor inner radius ri (μm) | 1730 |
| Rotor thickness h (um) | 77 |
| Mass of the rotor m (mg) | 0.457 |
| Moment of inertia of the rotor J (kg·m2) | 1.98 × 10−12 |
| Axial gap dz (μm) | 5 |
| Radial gap dr (μm) | 5 |
| Axial suspension electrode outer radius Ro (μm) | 1868 |
| Axial suspension electrode inner radius Ri (μm) | 1738 |
| Number of stator phases N | 3 |
| Number of stator electrodes Ns | 24 |
| Number of rotor poles Ns1 | 14 |
| Angle of rotor poles and stator electrodes θr | π/14 |
| Description (Unit) | Value |
|---|---|
| Rotor radial moment of inertia Je (kg·m2) | 7.86 × 10−13 |
| Spin rate of rotor ɷ0 (rpm) | 1.0 × 104 |
| Angular moment of rotor H (kg·m2·s−1) | 2.07 × 10−9 |
| Torque-voltage coefficient Kv (N·m·V−1) | 4.31 × 10−9 |
| Angular position stiffness Kf (N·m·rad−1) | 2.7 × 10−5 |
| Sensitivity of position sensor Ks (V·rad−1) | 5.9 × 102 |
| Rotor Speed | Scale Factor (mV/°/s) | |||
|---|---|---|---|---|
| Theoretical | Experimental | Nonlinearity | Asymmetry | |
| 1.0 × 104 rpm | 26.1 | 25.7 | 0.236% | 1.980% |
| 1.3 × 104 rpm | 33.9 | 33.9 | 0.120% | 0.678% |
| 1.5 × 104 rpm | 39.0 | 39.2 | 0.240% | 0.586% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Han, F. Analysis and Compensation of Bias Drift for a Micromachined Spinning-Rotor Gyroscope with Electrostatic Suspension. Sensors 2020, 20, 1799. https://doi.org/10.3390/s20061799
Wang S, Han F. Analysis and Compensation of Bias Drift for a Micromachined Spinning-Rotor Gyroscope with Electrostatic Suspension. Sensors. 2020; 20(6):1799. https://doi.org/10.3390/s20061799
Chicago/Turabian StyleWang, Shunyue, and Fengtian Han. 2020. "Analysis and Compensation of Bias Drift for a Micromachined Spinning-Rotor Gyroscope with Electrostatic Suspension" Sensors 20, no. 6: 1799. https://doi.org/10.3390/s20061799
APA StyleWang, S., & Han, F. (2020). Analysis and Compensation of Bias Drift for a Micromachined Spinning-Rotor Gyroscope with Electrostatic Suspension. Sensors, 20(6), 1799. https://doi.org/10.3390/s20061799





