Intensity Simulation of a Fourier Transform Infrared Spectrometer
Abstract
:1. Introduction
2. The Introduction of the Michelson Interferometer
2.1. The Principle of the Michelson Interferometer
2.2. The Off-Axis Effects of the Flat Array Detector
3. The Theoretical Framework of the Intensity Simulation of the GIIRS
3.1. Introduction of the Simulation Set
3.2. Computation of the ILS
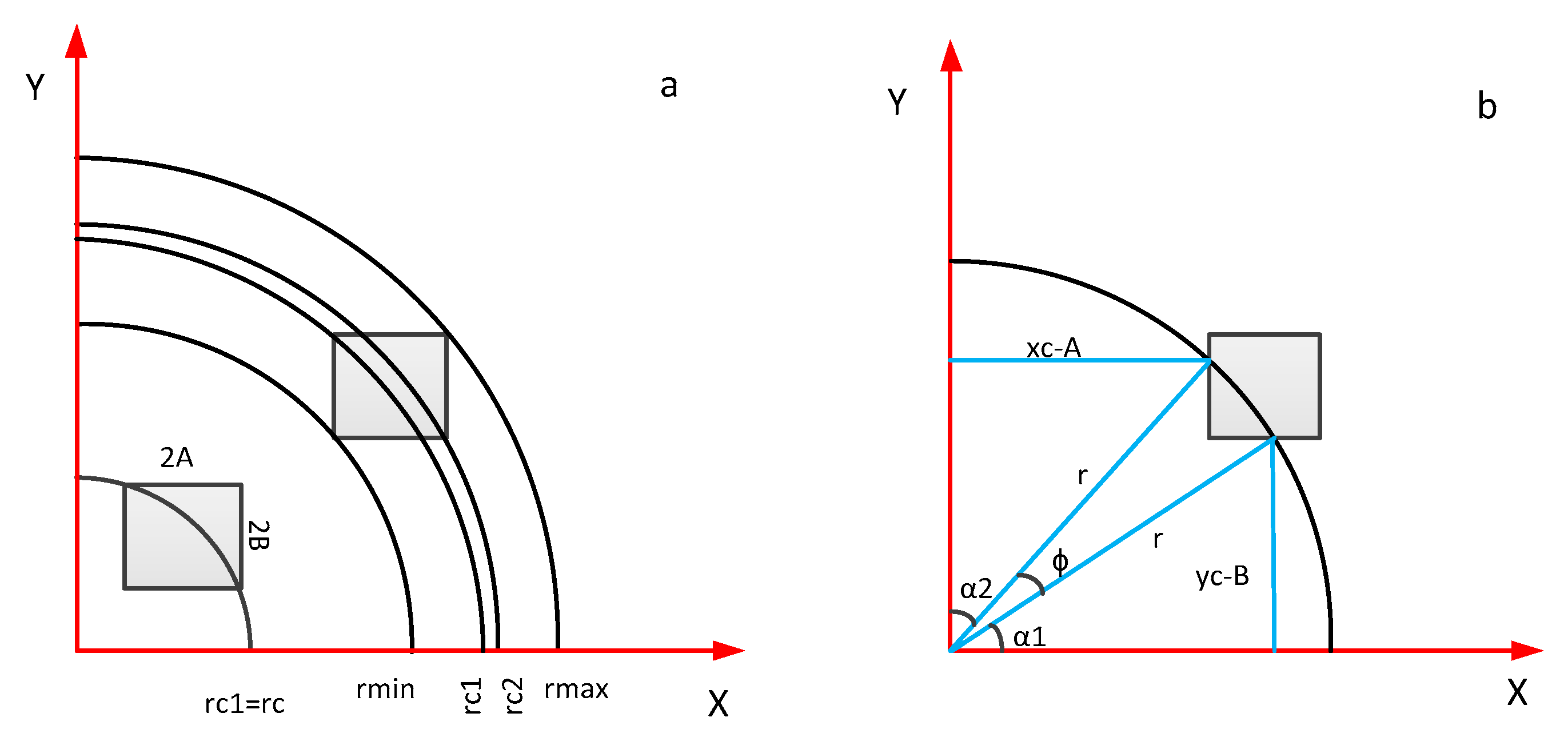
3.3. Intensity Computation of the Detector for the Off-Axis Position
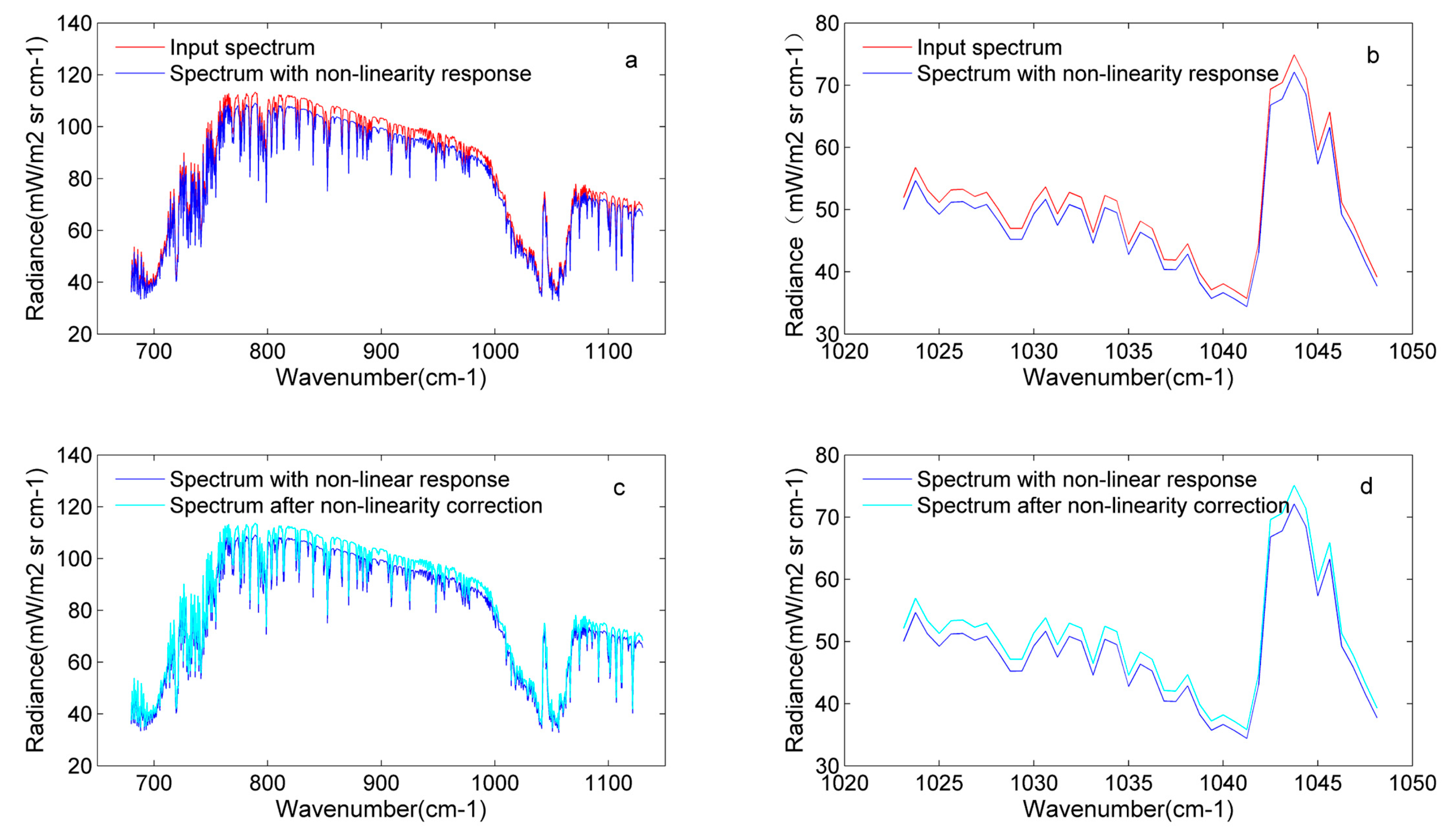
3.4. Nonlinearity Response of the Detector
4. Analysis of the Simulation Results of the Fourier Transform Spectrometer GIIRS
4.1. ILS for Various Positions of Detectors
4.2. Intensity Analysis with Off-Axis Effects
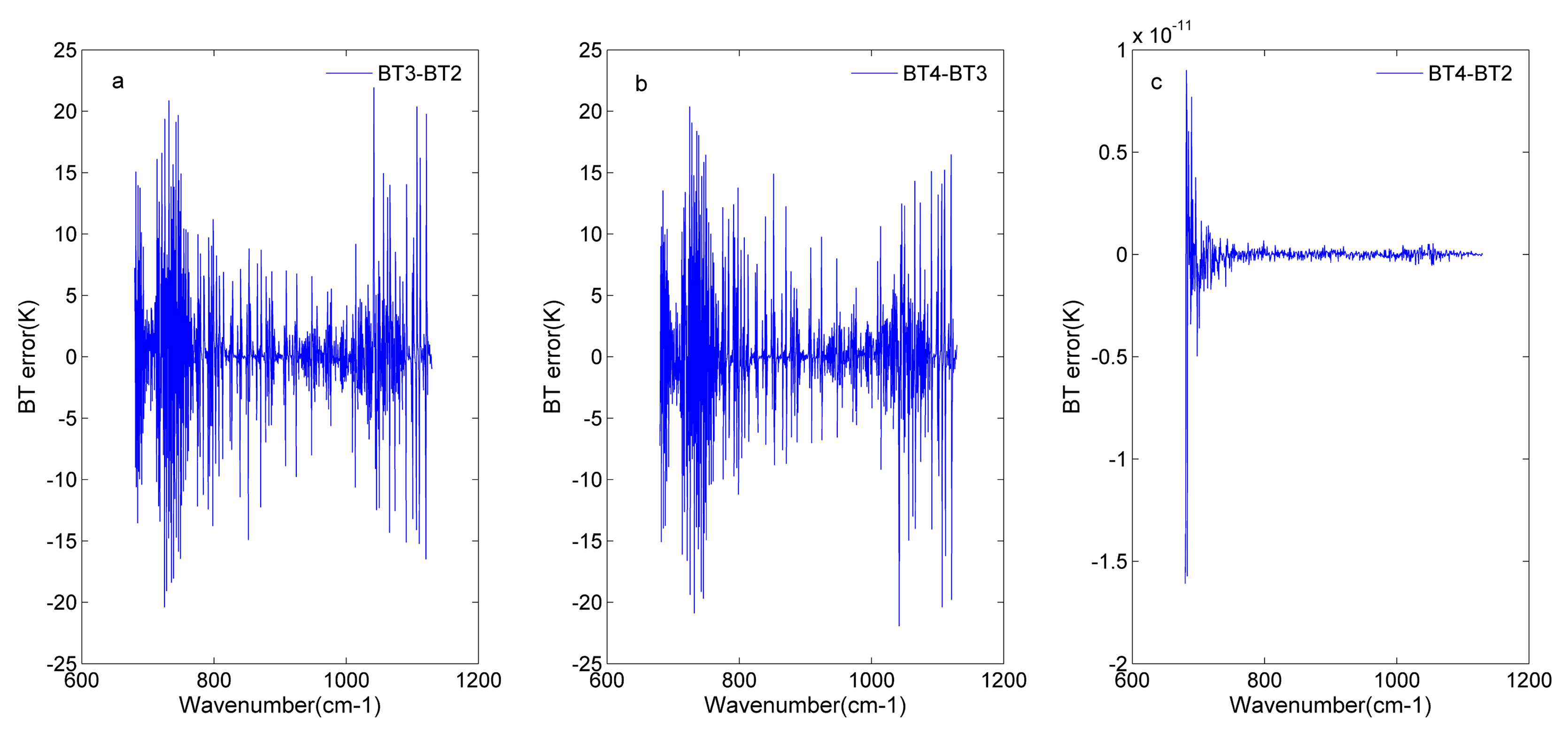
4.3. Analysis of the Nonlinearity Response
4.4. Intensity Simulation with Off-Axis Effects and the Non-Linearity Response
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| The Range of r | Corresponding wave-number range | ILS expression |
References
- Liu, J.; Wang, D.N. In-fiber beam splitters for construction of in-line Michelson interferometers. Opt. Lett. 2018, 43, 4304–4307. [Google Scholar] [CrossRef] [PubMed]
- Alain, F. Simulation of Imaging Fourier Transform Spectrometers using DIRSIG. Master’s Thesis, Rochester Institute of Technology, Rochester, NY, USA, 1999. [Google Scholar]
- Guelachili, G.; Fourier, Z.Z. Transform Spectroscopy; Peking University Press: Beijing, China, 1990. [Google Scholar]
- Chalon, G.; Cayla, F.; Diebel, D. IASI—An advanced sounder for operational meteorology. In Proceedings of the IAF, International Astronautical Congress, Toulouse, France, 22 May–2 June 1978. [Google Scholar]
- Blumstein, D.; Chalon, G.; Carlier, T.; Buil, C.; Hébert, P.; Maciaszek, T.; Ponce, G.; Phulpin, T.; Tournier, B.; Simeoni, D.; et al. IASI instrument: Technical overview and measured performances. Opt. Sci. Technol. Annu. Meet. 2004, 5543, 196–207. [Google Scholar]
- Hilton, F.; Armante, R.; August, T.; Barnet, C.; Bouchard, A.; Camy-Peyret, C.; Capelle, V.; Clerbaux, C.; Collard, A.; Dufour, G.; et al. Hyperspectral Earth Observation from IASI: Five Years of Accomplishments. Bull. Am. Meteorol. Soc. 2012, 93, 347–370. [Google Scholar] [CrossRef]
- ATBD, J.C. Joint Polar Satellite System (JPSS) Cross Track Infrared Sounder (CrIS) Sensor Data Records (SDR) Algorithm Theoretical Basic Document (ATBD); NASA: Greenbelt, MD, USA, 2014.
- Han, Y.; Revercomb, H.; Cromp, M.; Gu, D.; Johnson, D.; Mooney, D.; Scott, D.; Strow, L.; Bingham, G.; Borg, L.; et al. Suomi NPP CrIS measurements, sensor data record algorithm, calibration and validation activities, and record data quality. J. Geophys. Res. Atmos. 2013, 118, 734. [Google Scholar] [CrossRef]
- Predina, J.; Han, Y.; Mooney, D.; Atre, S.; Suwinski, L.; Predina, J. Future JPSS Cross-track Infrared Sounder (CrIS) Ground Calibration Algorithm Improvements. In Fourier Transform Spectroscopy and Hyperspectral Imaging and Sounding of the Environment; OSA Publishing: Laker Arrowhead, CA, USA, 2015. [Google Scholar]
- Lu, Q.; Zhou, F.; Qi, C.; Hu, X.; Xu, H.; Wu, C. Spectral performance evaluation of high-spectral resolution infrared atmospheric sounder onboard FY-3D. Opt. Precis. Eng. 2019, 27, 2105–2115. [Google Scholar]
- Chengli, Q.; Fang, Z.; Chunqiang, W.; Xiuqing, H.; Mingjian, G. Spectral calibration technique of Fengyun-3 satellite High-spectral Resolution Infrared Sounder. Opt. Precis. Eng. 2019, 27, 747. [Google Scholar]
- Zhou, F. Inversion and Accuracy Verification of Spectral Calibration Parameters for Spaceborne Infrared Hyperspectral Instrument. Master’s Thesis, Chinese Academy of Meteorological Sciences, Beijing, China, 2019. [Google Scholar]
- Zhang, Z.; Lu, F.; Fang, X.; Tang, S.; Zhang, X.; Xu, Y.; Han, W.; Nie, S.; Shen, Y.; Zhou, Y. Applicatuib and Development of FY-4 Meteorological Satellite. Aerosp. Shanghai 2017, 8–19. [Google Scholar]
- Hua, J.H.J.; Wang, Z.W.Z.; Duan, J.D.J.; Li, L.L.L.; Zhang, C.Z.C.; Wu, X.W.X.; Fan, Q.F.Q.; Chen, R.C.R.; Sun, X.S.X.; Zhao, L.Z.L.; et al. Review of Geostationary Interferometric Infrared Sounder. Chin. Opt. Lett. 2018, 16, 111203. [Google Scholar]
- Eismann, M.T.; Schwartz, C.R.; Cederquist, J.N.; Hackwell, J.A.; Huppi, R.J. Comparison of infrared imaging hyperspectral sensors for military target detection applications. Int. Symp. Opt. Sci. Eng. Instrum. 1996, 2819, 91–102. [Google Scholar]
- Gomer, N.R.; Gardner, C.W.; Nelson, M.P. Handheld and mobile hyperspectral imaging sensors for wide-area standoff detection of explosives and chemical warfare agents. Next-Gener. Spectrosc. Technol. IX 2016, 9855, 98550. [Google Scholar]
- Martynov, D.V.; Hall, E.D.; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Adams, C.; Adhikari, R.X.; Anderson, R.A.; Anderson, S.B.; Arai, K.; et al. Sensitivity of the Advanced LIGO detectors at the beginning of gravitational wave astronomy. Phys. Rev. D 2016, 93, 112004. [Google Scholar] [CrossRef] [Green Version]
- Pöller, F.; Bloise, F.S.; Jakobi, M.; Wang, S.; Dong, J.; Koch, A. Non-Contact Roughness Measurement in Sub-Micron Range by Considering Depolarization Effects. Sensors 2019, 19, 2215. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seaman, S.T.; Cook, A.; Scola, S.J.; Hostetler, C.A.; Miller, I.; Welch, W. Performance characterization of a pressure-tuned wide-angle Michelson interferometric spectral filter for high spectral resolution lidar. Lidar Remote Sens. Environ. Monit. XV 2015, 9612, 96120. [Google Scholar]
- Xu, J.; Schreier, F.; Loyola, D.; Schüssler, O.; Doicu, A.; Trautmann, T. Monitoring ozone in different spectral regimes from space and balloon (Sentinel-4/-5P, TELIS). In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 360–363. [Google Scholar]
- Lee, J.H.; Kim, H.J.; Kim, J.-S.; Nam, H.; Kang, Y.I. Development of compact stand-off hazardous chemical detector based on Michelson interferometer. Opt. Eng. 2018, 57, 084105. [Google Scholar] [CrossRef]
- Kara, O.; Sweeney, F.; Rutkauskas, M.; Farrell, C.; Leburn, C.G.; Reid, D.T. Open-Path Mid-Infrared Remote Sensing of Atmospheric Gases Using a Broadband Optical Parametric Oscillator. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 5 May 2019. [Google Scholar]
- Bernard, F.; Calvel, B. Iasi-ng: An innovative wide field infrared remote sensing fts for meteorology, atmospheric chemistry and climate monitoring. In Proceedings of the Optical Sensors and Sensing Congress (ES, FTS, HISE, Sensors), San Jose, CA, USA, 25 June 2019. [Google Scholar]
- Harlander, J.M.; Englert, C.R. A Velocity Modulated Fixed-Path Michelson Interferometer for Space-Based Remote Sensing of Upper Atmospheric Neutral Winds. In Proceedings of the Conference on Lasers and Electro-Optics, San Jose, CA, USA, 5 May 2019. [Google Scholar]
- Lindner, C.; Wolf, S.; Kiessling, J.; Kuehnemann, F. Fourier transform infrared spectroscopy with visible light. Opt. Express 2020, 28, 4426–4432. [Google Scholar] [CrossRef] [PubMed]
- Zavyalov, V.V.; Fish, C.S.; Bingham, G.E.; Esplin, M.; Greenman, M.; Scott, D.; Han, Y. Preflight assessment of the cross-track infrared sounder (CrIS) performance. SPIE Remote Sens. 2011, 8176, 817606. [Google Scholar]
- Yang, J.; Zhang, Z.; Wei, C.; Lu, F.; Guo, Q. Introducing the New Generation of Chinese Geostationary Weather Satellites, Fengyun-4. Bull. Am. Meteorol. Soc. 2017, 98, 1637–1658. [Google Scholar] [CrossRef]
- Griffiths, P.R.; De Haseth, J.A. Fourier Transform Infrared Spectrometry; Wiley: Hoboken, NJ, USA, 2007; Volume 171. [Google Scholar]
- Ahro, M.; Kauppinen, J.; Salomaa, I. Detection and correction of instrumental line-shape distortions in fourier spectroscopy. Appl. Opt. 2000, 39, 6230–6237. [Google Scholar] [CrossRef]
- Liu, P.; Wang, P.-g.; Hua, J.-w.; Yang, L.-z. Spectral calibration of the space-borne Fourier transform spectrometer. Opt. Electron. Eng. 2008, 35, 109–113. [Google Scholar]
- Lei, Z.; Minzhu, Y.; Yaopu, Z.; ChangPei, H. Instrument line shape of infrared Fourier transform spectrometer and its engineer applications. Opt. Precis. Eng. 2015, 23, 3322–3328. [Google Scholar]
- Saunders, R.; Hocking, J.; Turner, E.; Rayer, P.; Rundle, D.; Brunel, P.; Vidot, J.; Roquet, P.; Matricardi, M.; Geer, A.; et al. An update on the RTTOV fast radiative transfer model (currently at version 12). Geosci. Model Dev. 2018, 11, 2717–2737. [Google Scholar] [CrossRef] [Green Version]
- Genest, J.; Tremblay, P. Instrument line shape of fourier transform spectrometers: Analytic solutions for nonuniformly illuminated off-axis detectors. Appl. Opt. 1999, 38, 5438–5446. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Zhou, Y.; Zhang, L.; Han, C. Correction to Nonlinearity in Interferometric Data and Its Effect on Radiometric Calibration. Chin. J. Lasers 2017, 44, 110002. [Google Scholar] [CrossRef]












| Parameters | Interpretation |
|---|---|
| Itotal | The total intensity (DC part + AC part) |
| I | The interference intensity |
| E0 | Amplitude |
| X | Optical path difference |
| λ | Wavelength of the input light |
| σ | Actual wavenumber of the input light (σ = 1/λ) |
| σn | Apparent wavenumber of the input light, |
| B | The intensity for DC part |
| R | Distance from the detector to the center of focal plane |
| f | Focal length |
| φ | The opening angle of the arc segmented by the detector |
| rc1, rc2, rmin, rmax | The distance between the detector and the optical axis |
| xc | Half height of the square detector |
| yc | Half width of the square detector |
| α1, α2 | Opening angles of different arcs |
| Ω | The solid angle |
| θ | Off-axis angle |
| Spec | The measured spectrum |
| I | The ideal signal |
| m | The actual interference signal |
| The nonlinear parameter |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, Z.; Lu, Q.; Xu, Y.; Huo, H. Intensity Simulation of a Fourier Transform Infrared Spectrometer. Sensors 2020, 20, 1833. https://doi.org/10.3390/s20071833
Ni Z, Lu Q, Xu Y, Huo H. Intensity Simulation of a Fourier Transform Infrared Spectrometer. Sensors. 2020; 20(7):1833. https://doi.org/10.3390/s20071833
Chicago/Turabian StyleNi, Zhuoya, Qifeng Lu, Yishu Xu, and Hongyuan Huo. 2020. "Intensity Simulation of a Fourier Transform Infrared Spectrometer" Sensors 20, no. 7: 1833. https://doi.org/10.3390/s20071833
APA StyleNi, Z., Lu, Q., Xu, Y., & Huo, H. (2020). Intensity Simulation of a Fourier Transform Infrared Spectrometer. Sensors, 20(7), 1833. https://doi.org/10.3390/s20071833





