Frequency-Coded Chipless RFID Tags: Notch Model, Detection, Angular Orientation, and Coverage Measurements
Abstract
1. Introduction
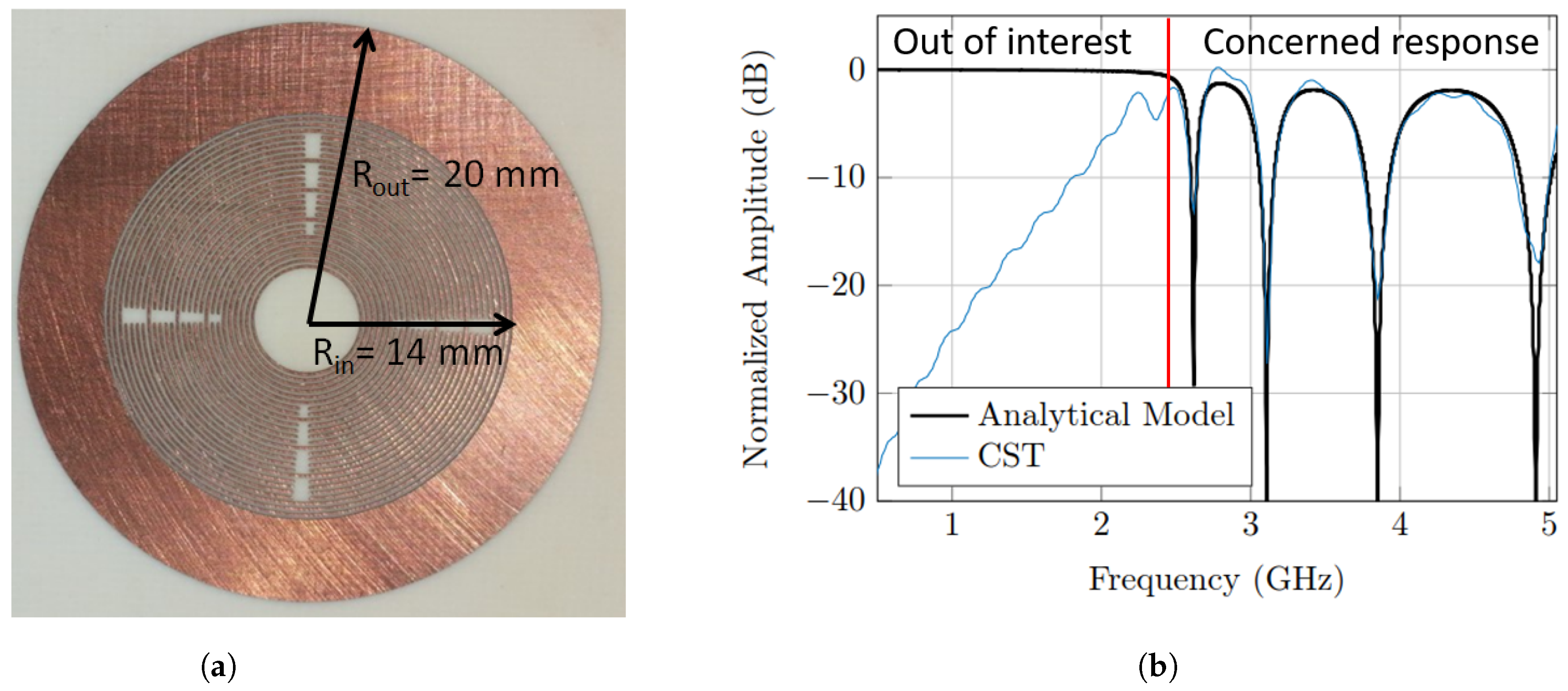
2. Notch Analytical Model and Notch Detection
2.1. Notch Analytical Model
2.2. Notch Detection
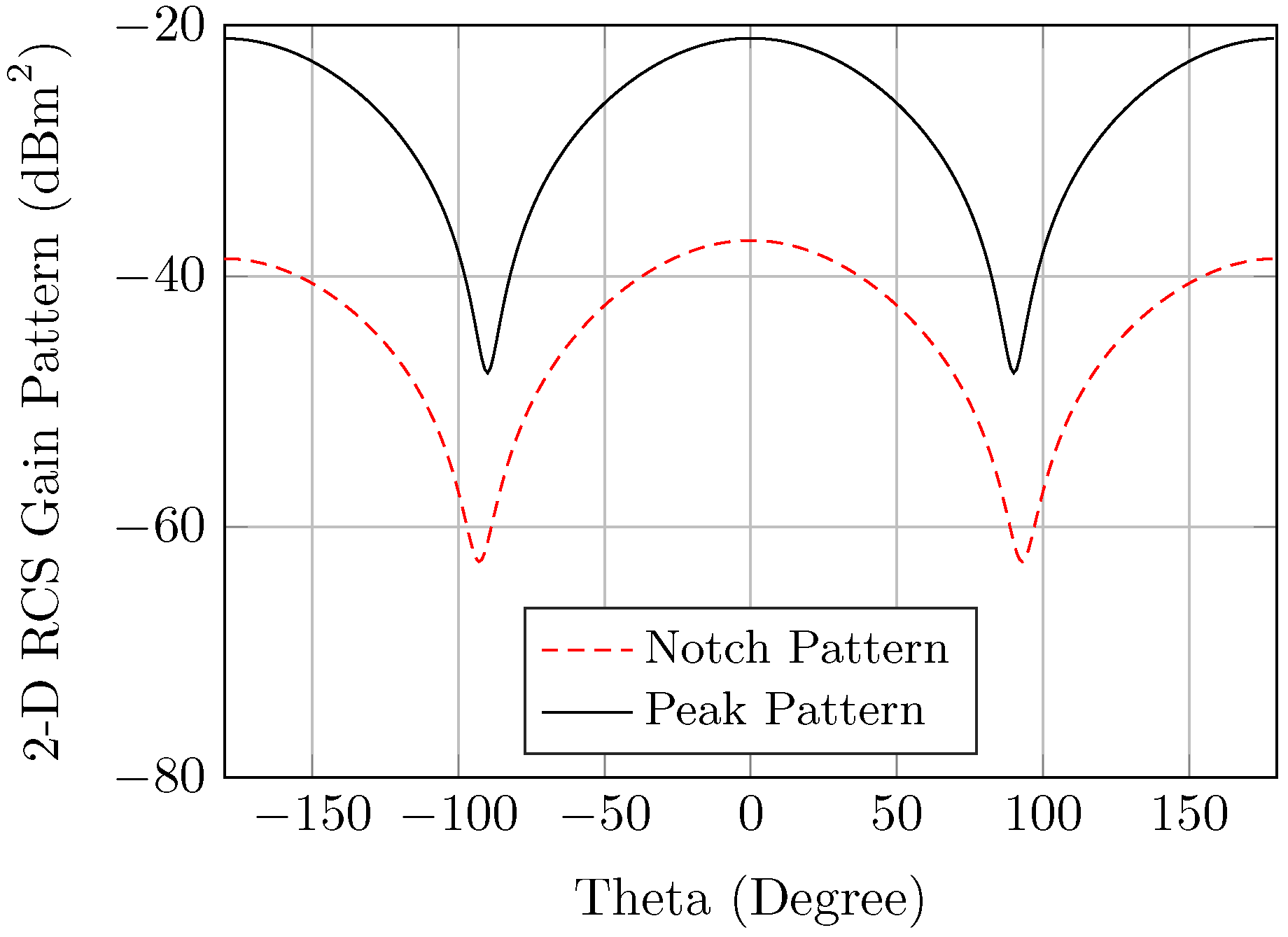
3. Angular Displacement
3.1. Elevation Orientation Displacement
3.2. Azimuth Orientation Displacement
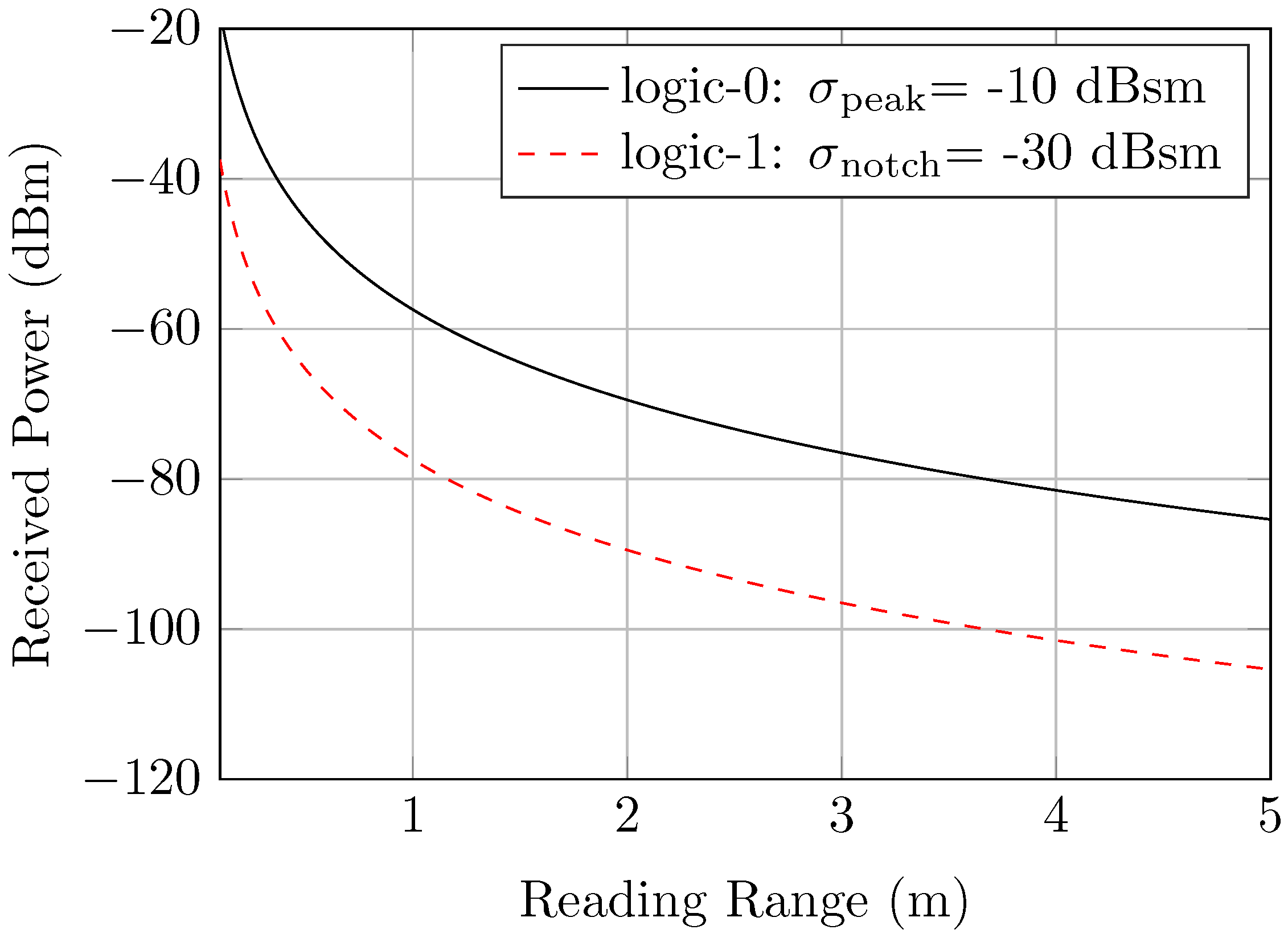
4. Reading Range
5. FC Tags: Measurement Errors and Limitations
6. FC Tags Measurements
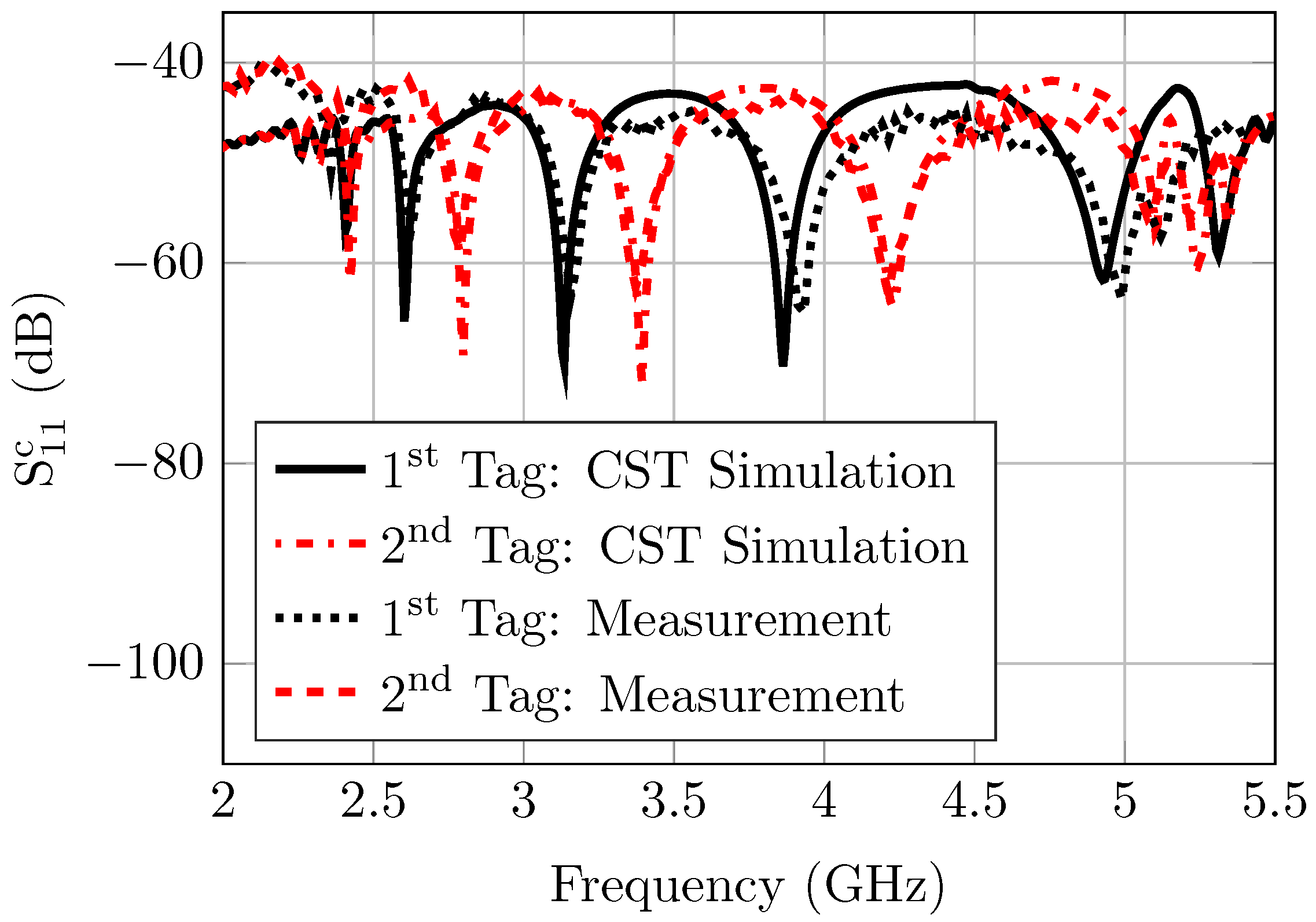
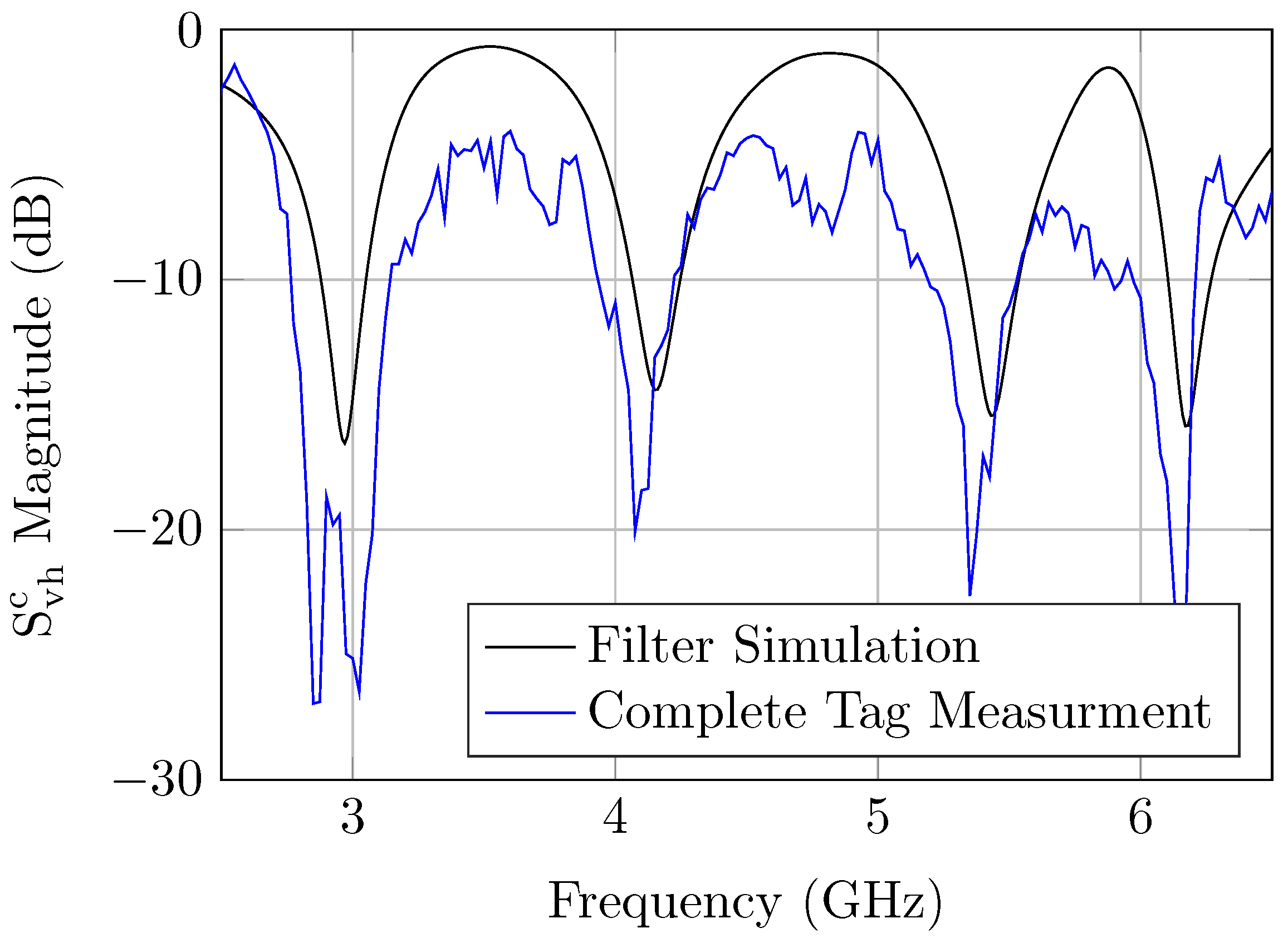
6.1. RCS and Depolarizing Tags’ Measurements
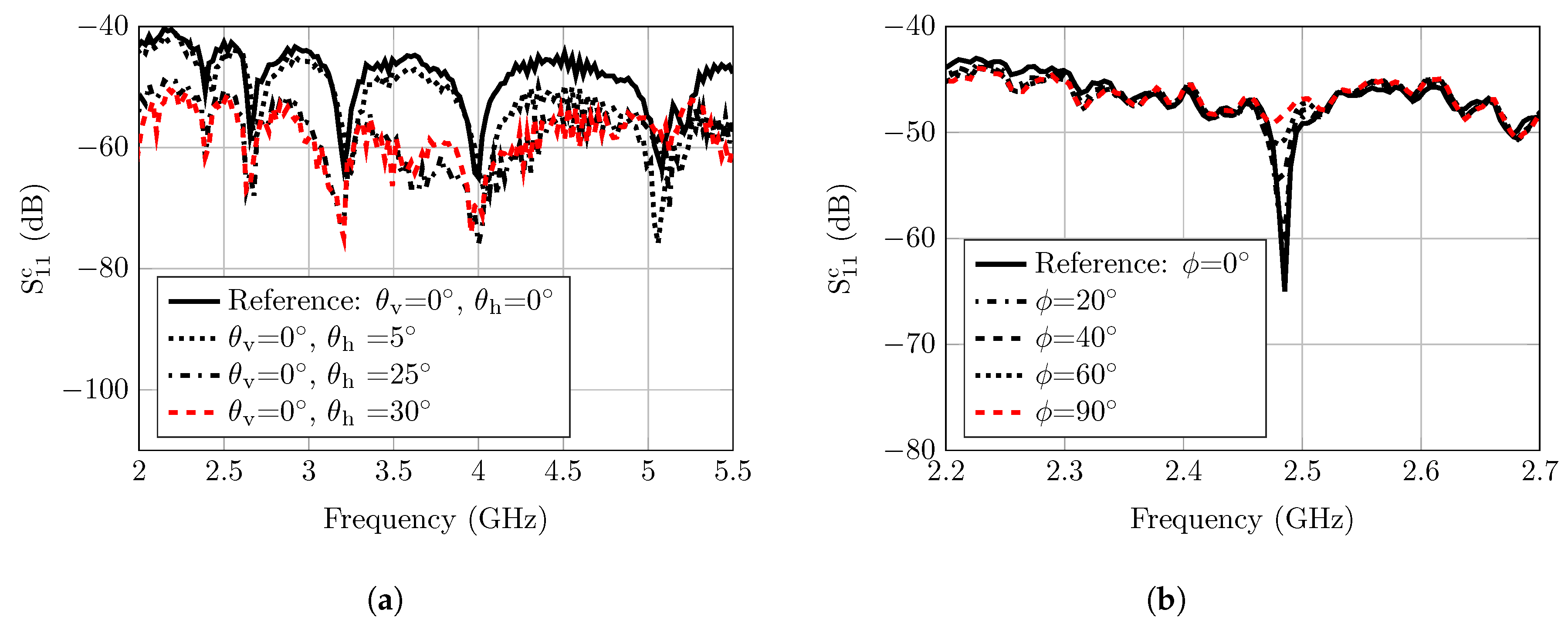
6.2. Elevation Orientation Displacement Measurement
6.3. Azimuth Orientation Displacement Measurement
6.4. Range Measurement
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lazaro, A.; Villarino, R.; Costa, F.; Genovesi, S.; Gentile, A.; Buoncristiani, L.; Girbau, D. Chipless Dielectric Constant Sensor for Structural Health Testing. IEEE Sens. J. 2018, 18, 5576–5585. [Google Scholar] [CrossRef]
- Betancourt, D.; Barahona, M.; Haase, K.; Schmidt, G.; Hübler, A.; Ellinger, F. Design of Printed Chipless-RFID Tags With QR-Code Appearance Based on Genetic Algorithm. IEEE Trans. Antennas Propag. 2017, 65, 2190–2195. [Google Scholar] [CrossRef]
- Svanda, M.; Havlicek, J.; Machac, J.; Polivka, M. Polarization independent chipless RFID tag based on circular arrangement of dual-spiral capacitively-loaded dipoles with robust RCS response. IET Microwaves Antennas Propag. 2018, 12, 2167–2171. [Google Scholar] [CrossRef]
- Costa, F.; Borgese, M.; Gentile, A.; Buoncristiani, L.; Genovesi, S.; Dicandia, F.A.; Bianchi, D.; Monorchio, A.; Manara, G. Robust Reading Approach for Moving Chipless RFID Tags by Using ISAR Processing. IEEE Trans. Microw. Theory Tech. 2018, 66, 2442–2451. [Google Scholar] [CrossRef]
- Khaliel, M.; El-Awamry, A.; Megahed, A.F.; Kaiser, T. A Novel Design Approach for Co/Cross-Polarizing Chipless RFID Tags of High Coding Capacity. IEEE J. Radio Freq. Identif. 2017, 1, 135–143. [Google Scholar] [CrossRef]
- Jiménez-Sáez, A.; Schüßler, M.; Nickel, M.; Jakoby, R. Hybrid Time-Frequency Modulation Scheme for Chipless Wireless Identification and Sensing. IEEE J. Radio Freq. Identif. 2018, 18, 7850–7859. [Google Scholar] [CrossRef]
- Shao, B.; Chen, Q.; Amin, Y.; David, S.M.; Liu, R.; Zheng, L.R. An Ultra-low-cost RFID Tag with 1.67 Gbps Data Rate by Ink-jet Printing on Paper Substrate. In Proceedings of the IEEE Asian Solid-State Circuits Conference, Beijing, China, 8–10 November 2010. [Google Scholar]
- Kim, J.; Banks, A.; Xie, Z.; Heo, S.Y.; Gutruf, P.; Lee, J.W.; Xu, S.; Jang, K.-I.; Liu, F.; Brown, G.; et al. Miniaturized Flexible Electronic Systems with Wireless Power and Near-Field Communication Capabilities. Adv. Funct. Mater. 2015, 25, 4761–4767. [Google Scholar] [CrossRef]
- Lee, H.E.; Lee, D.; Lee, T.I.; Shin, J.H.; Choi, G.M.; Kim, C.; Lee, S.H.; Lee, J.H.; Kim, Y.H.; Kang, S.-M.; et al. Wireless Powered Wearable Micro Light-Emitting Diodes. Nano Energy 2019, 55, 454–462. [Google Scholar] [CrossRef]
- Echevarria, J.J.; Ruiz-de-Garibay, J.; Legarda, J.; Álvarez, M.; Ayerbe, A.; Vazquez, J.I. Web Tag: Web browsing into sensor tags over NFC. Sensors 2012, 12, 8675–8690. [Google Scholar] [CrossRef]
- Khaliel, M.; Fawky, A.; El-Awamry, A.; Mahmoud, A.E.; Kaiser, T. Printable, high coding capacity chipless RFID tags for low-cost item tagging. In Proceedings of the IEEE International Conference on Networking, Sensing and Control (ICNSC), Calabria, Italy, 16–18 May 2017; pp. 351–355. [Google Scholar]
- Zumbahlen, H. Basic Linear Design; Analog Devices, Inc.: Norwood, MA, USA, 2007; Chapter 8; p. 11. [Google Scholar]
- Fawky, A.; Khaliel, M.; El-Awamry, A.; El-Hadidy, M.; Kaiser, T. Novel pseudo-noise coded chipless rfid system for clutter removal and tag detection. In Proceedings of the IEEE International Conference on RFID, San Diego, CA, USA, 15–17 April 2015; pp. 100–104. [Google Scholar]
- El-Awamry, A.; Khaliel, M.; Fawky, A.; El-Hadidy, M.; Kaiser, T. Novel notch modulation algorithm for enhancing the chipless rfid tags coding capacity. In Proceedings of the IEEE International Conference on RFID, San Diego, CA, USA, 15–17 April 2015; pp. 25–31. [Google Scholar]
- Couch, L.W., II. Digital and Analog Communication Systems, 6th ed.; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Xu, L.; Feng, D.; Wang, X. Matched-filter properties of linear-frequency-modulation radar signal reflected from a phase-switched screen. IET Radar Sonar Navig. 2016, 10, 318–324. [Google Scholar] [CrossRef]
- Johnston, A. Improvements to a pulse compression radar matched filter. Radio Electron. Eng. 1983, 53, 138–140. [Google Scholar] [CrossRef]
- Sussman, S. A matched filter communication system for multipath channels. IRE Trans. Inf. Theory 1960, 6, 367–373. [Google Scholar] [CrossRef]
- Wang, L.; Liu, T.; Sidén, J.; Wang, G. Design of Chipless RFID Tag by Using Miniaturized Open-Loop Resonators. IEEE Trans. Antennas Propag. 2018, 66, 618–626. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, W.; Li, L.; Han, L.; Chen, X.; Yang, R.; Zeng, Q. A Resistance-Type Sensor Based on Chipless RFID. IEEE Trans. Antennas Propag. 2017, 65, 3319–3325. [Google Scholar] [CrossRef]
- Feng, C.; Zhang, W.; Li, L.; Han, L.; Chen, X.; Ma, R. Angle-Based Chipless RFID Tag with High Capacity and Insensitivity to Polarization. IEEE Trans. Antennas Propag. 2017, 63, 1789–1797. [Google Scholar] [CrossRef]
- Rezaiesarlak, R.; Manteghi, M. Design of Chipless RFID Tags Based on Characteristic Mode Theory (CMT). IEEE Trans. Antennas Propag. 2015, 63, 711–718. [Google Scholar] [CrossRef]
- Vena, A.; Perret, E.; Tedjini, S. High-Capacity Chipless RFID Tag Insensitive to the Polarization. IEEE Trans. Antennas Propag. 2012, 60, 4509–4515. [Google Scholar] [CrossRef]
- Islam, M.A.; Karmakar, N.C. Compact Printable Chipless RFID Systems. IEEE Trans. Microw. Theory Tech. 2015, 63, 3785–3793. [Google Scholar] [CrossRef]
- Ashraf, M.A. Design and Analysis of Multi- Resonators Loaded Broadband Antipodal Tapered Slot Antenna for Chipless RFID Applications. IEEE Access 2017, 5, 25798–25807. [Google Scholar] [CrossRef]
- Khaliel, M.; El-Awamry, A.; Fawky, A.; El-Hadidy, M.; Kaiser, T. A novel co/cross-polarizing chipless RFID tags for high coding capacity and robust detection. In Proceedings of the IEEE International Symposium on Antennas and Propagation USNC/URSI National Radio Science Meeting, Vancouver, BC, Canada, 19–24 July 2015; pp. 159–160. [Google Scholar]
- Khaliel, M.; El-Awamry, A.; Fawky, A.; Kaiser, T. Long Reading Range Chipless RFID System Based on Reflectarray Antennas. In Proceedings of the European Conference on Antennas and Propagation (EuCAP), Paris, France, 19–24 March 2017. [Google Scholar]
- Khaliel, M.; El-Awamry, A.; Fawky, A.; Kaiser, T. Long reading range for the frequency coded Chipless RFID system based on reflectarray antennas. Int. J. Microw. Wirel. Technol. 2018, 10, 187–195. [Google Scholar] [CrossRef]
- Wiesbeck, W.; Kahny, D. Single reference, three target calibration and error correction for monostatic, polarimetric free space measurements. Proc. IEEE 1991, 79, 1551–1558. [Google Scholar] [CrossRef]
- Sevgi, L.; Rafiq, Z.; Majid, I. Radar cross section (RCS) measurements [Testing ourselves]. IEEE Antennas Propag. Mag. 2013, 55, 277–291. [Google Scholar] [CrossRef]









| Parameters | NFC | Chipless RFID |
|---|---|---|
| Antenna Size | Bigger | Smaller |
| Operating Frequency | 13.56 MHz | UWB |
| Transfer Efficiency | Lower(Nearfield Antenna) | Higher (Farfield Antenna) |
| Power Transfer | Depends on mutual coupling | Depends on the RCS of the chipless tag |
| Distance | <0.1 m | Can achieve 2 m and more |
| 2.618 | 112 | 23.750 | 1 |
| 3.108 | 266 | 11.6842 | 1 |
| 3.85 | 448 | 8.5938 | 1 |
| 4.91 | 592 | 8.2939 | 1 |
| 2.26 | 41.0909 | 55 | 1 |
| 2.53 | 46 | 55 | 1 |
| 2.89 | 36.125 | 80 | 1 |
| 4.63 | 46.3 | 100 | 1 |
| Figure Number | Modulation (Coding) | Size (mm) | Resonator Type | Polarization | Coding Capacity | |
|---|---|---|---|---|---|---|
| RCS-based | Figure 1a | Notch Postion | Ring | Independent | Moderate | |
| Figure 2a | Notch Postion and Width | Patch, square ring, and dipole | Linear | High | ||
| Figure 7a | Notch Postion | Dipole | Linear | Low | ||
| Retransmission-based | Figure 12 | Notch Postion | Slot | Dual | Low |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alam, J.; Khaliel, M.; Fawky, A.; El-Awamry, A.; Kaiser, T. Frequency-Coded Chipless RFID Tags: Notch Model, Detection, Angular Orientation, and Coverage Measurements. Sensors 2020, 20, 1843. https://doi.org/10.3390/s20071843
Alam J, Khaliel M, Fawky A, El-Awamry A, Kaiser T. Frequency-Coded Chipless RFID Tags: Notch Model, Detection, Angular Orientation, and Coverage Measurements. Sensors. 2020; 20(7):1843. https://doi.org/10.3390/s20071843
Chicago/Turabian StyleAlam, Jahangir, Maher Khaliel, Abdelfattah Fawky, Ahmed El-Awamry, and Thomas Kaiser. 2020. "Frequency-Coded Chipless RFID Tags: Notch Model, Detection, Angular Orientation, and Coverage Measurements" Sensors 20, no. 7: 1843. https://doi.org/10.3390/s20071843
APA StyleAlam, J., Khaliel, M., Fawky, A., El-Awamry, A., & Kaiser, T. (2020). Frequency-Coded Chipless RFID Tags: Notch Model, Detection, Angular Orientation, and Coverage Measurements. Sensors, 20(7), 1843. https://doi.org/10.3390/s20071843







