Extremely Sensitive Microwave Sensor for Evaluation of Dielectric Characteristics of Low-Permittivity Materials
Abstract
:1. Introduction
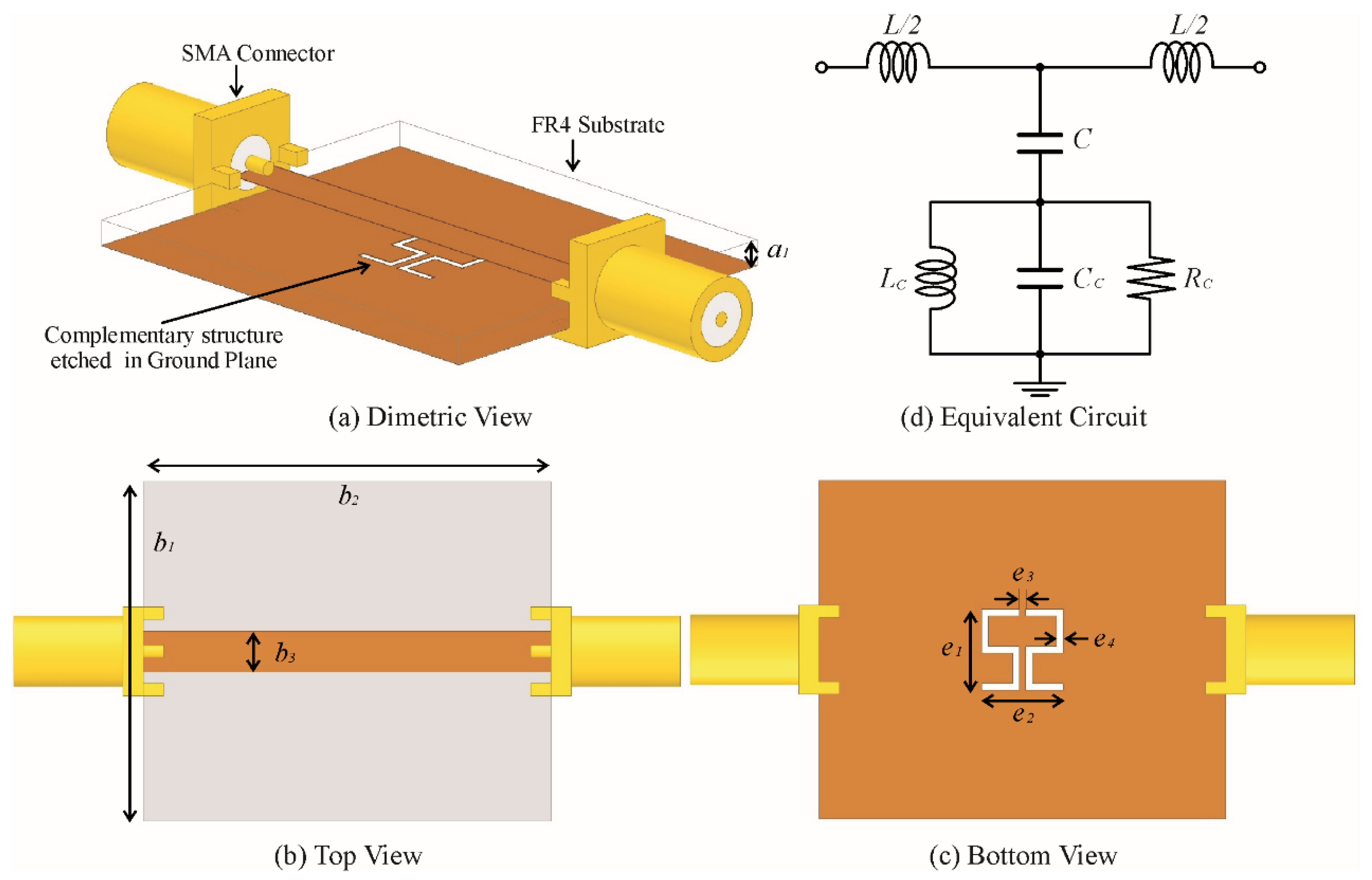
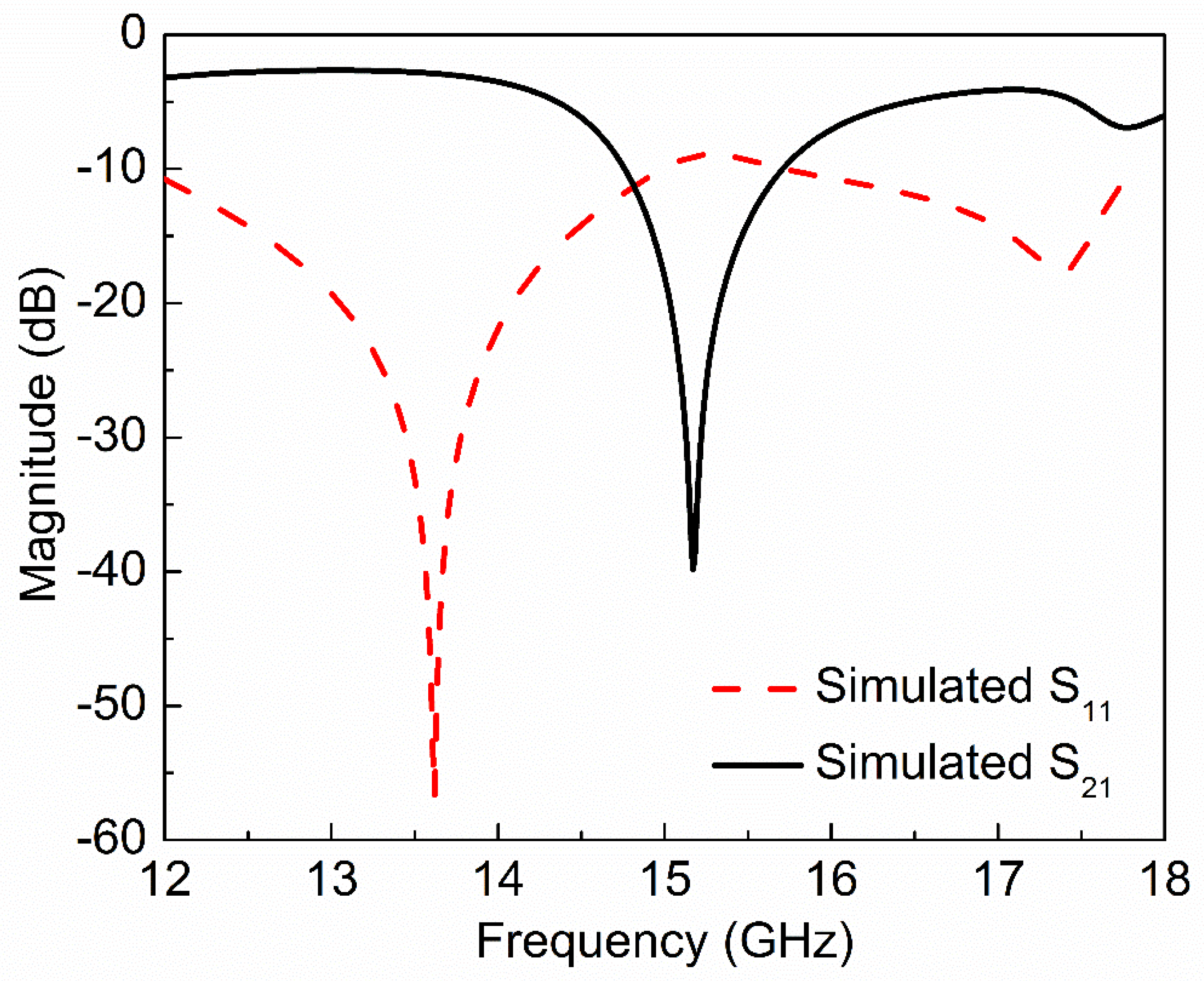
2. Design and Simulation of Proposed Sensor
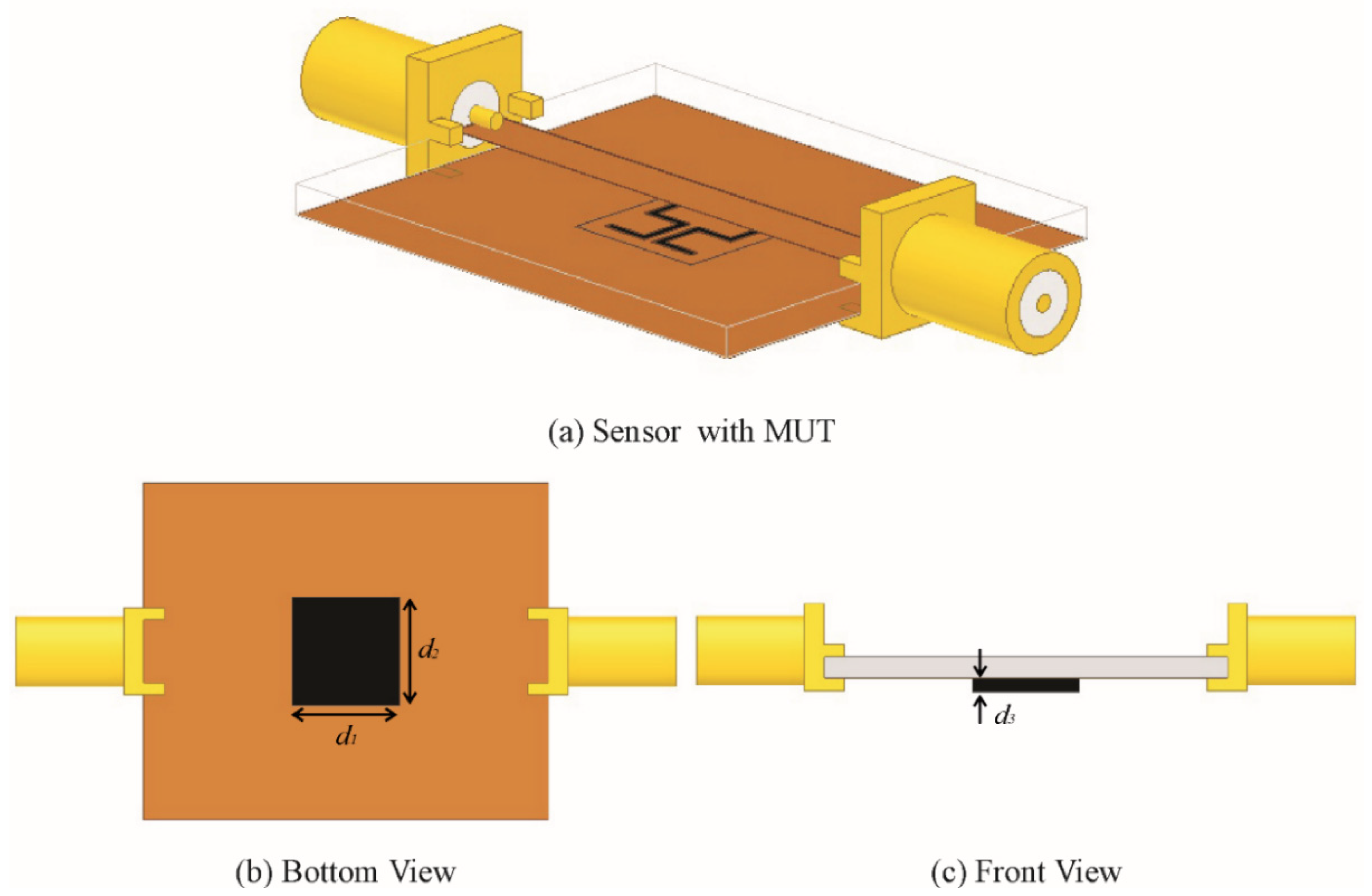
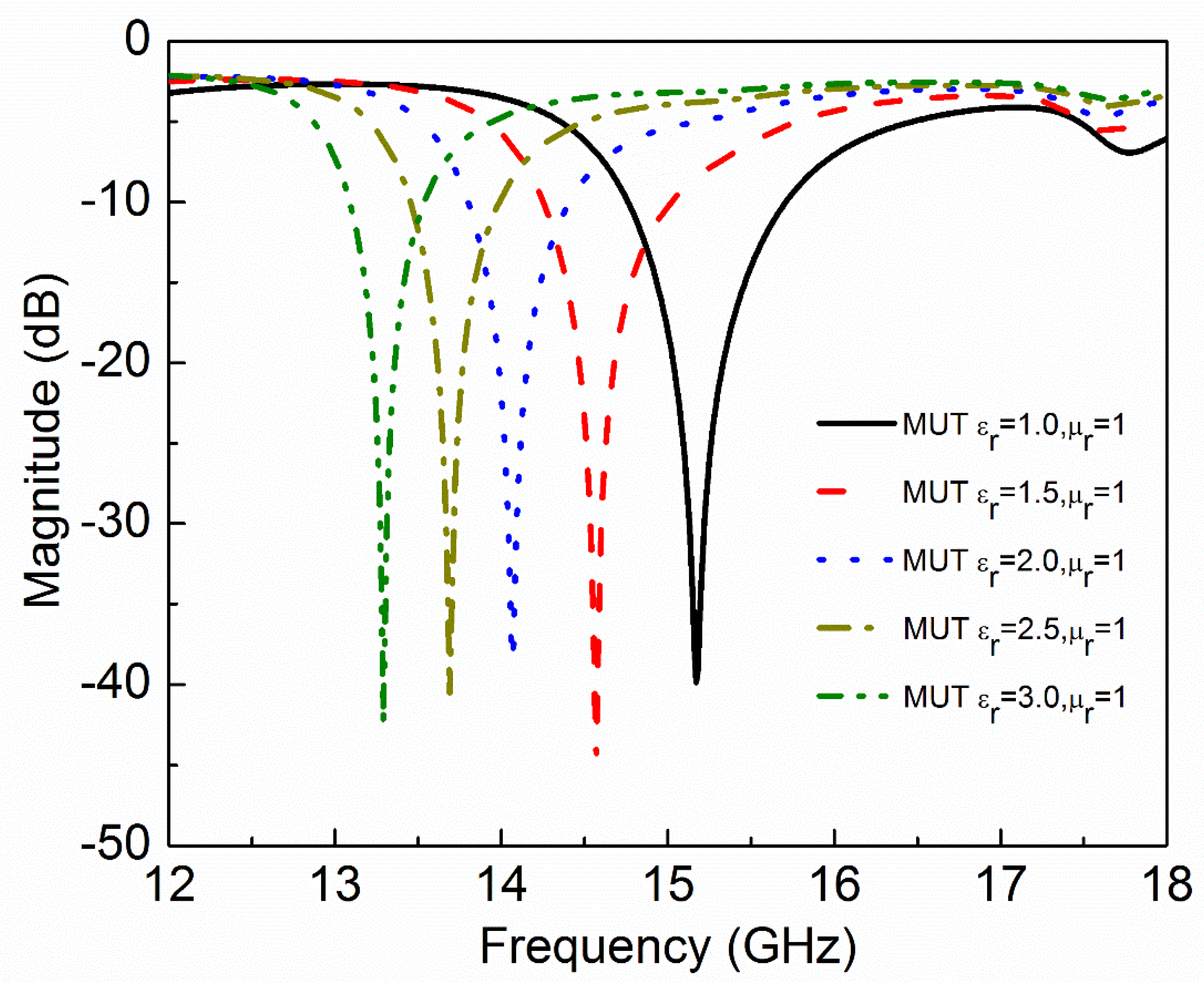
3. Measurement and Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Trabelsi, S.; Nelson, S.O. Microwave sensing of quality attributes of agricultural and food products. IEEE Instrum. Meas. Mag. 2016, 19, 36–41. [Google Scholar] [CrossRef]
- Wagner, N.; Emmerich, K.; Bonitz, F.; Kupfer, K. Experimental Investigations on the Frequency- and Material Properties of Soil. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2518–2530. [Google Scholar] [CrossRef]
- Puentes, M.; Maasch, M.; Schubler, M.; Jakoby, R. Frequency multiplexed 2-dimensional sensor array based on split-ring resonators for organic tissue analysis. IEEE Trans. Microw. Theory Tech. 2012, 60, 1720–1727. [Google Scholar] [CrossRef]
- RoyChoudhury, S.; Rawat, V.; Jalal, A.H.; Kale, S.N.; Bhansali, S. Recent advances in metamaterial split-ring-resonator circuits as biosensors and therapeutic agents. Biosens. Bioelectron. 2016, 86, 595–608. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, H.J.; Lee, J.H.; Moon, H.S.; Jang, I.S.; Choi, J.S.; Yook, J.G.; Jung, H.I. A planar split-ring resonator-based microwave biosensor for label-free detection of biomolecules. Sensors Actuators, B Chem. 2012, 169, 26–31. [Google Scholar] [CrossRef]
- Zarifi, M.H.; Sadabadi, H.; Hejazi, S.H.; Daneshmand, M.; Sanati-Nezhad, A. Noncontact and Nonintrusive Microwave-Microfluidic Flow Sensor for Energy and Biomedical Engineering. Sci. Rep. 2018, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Schueler, M.; Mandel, C.; Puentes, M.; Jakoby, R. Metamaterial inspired microwave sensors. IEEE Microw. Mag. 2012, 13, 57–68. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Zarifi, M.H.; Pedrycz, W.; Daneshmand, M. Robust Ultra-High Resolution Microwave Planar Sensor Using Fuzzy Neural Network Approach. IEEE Sens. J. 2017, 17, 323–332. [Google Scholar] [CrossRef]
- Zarifi, M.H.; Deif, S.; Abdolrazzaghi, M.; Chen, B.; Ramsawak, D.; Amyotte, M.; Vahabisani, N.; Hashisho, Z.; Chen, W.; Daneshmand, M. A microwave ring resonator sensor for early detection of breaches in pipeline coatings. IEEE Trans. Ind. Electron. 2017, 65, 1626–1635. [Google Scholar] [CrossRef]
- Zarifi, M.H.; Daneshmand, M. Monitoring Solid Particle Deposition in Lossy Medium Using Planar Resonator Sensor. IEEE Sens. J. 2017, 17, 7981–7989. [Google Scholar] [CrossRef]
- Kumari, R.; Patel, P.N.; Yadav, R. An ENG-Inspired Microwave Sensor and Functional Technique for Label-Free Detection. IEEE Sens. J. 2018, 18, 3932–3939. [Google Scholar] [CrossRef]
- Machac, J. Amorphous Metamaterial with Negative Permeability. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2138–2141. [Google Scholar] [CrossRef]
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental verification of a negative index of refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ji, L.; Varadan, V.V. Negative refractive index and negative refraction of waves in lossy metamaterials. Electron. Lett. 2016, 52, 260–262. [Google Scholar] [CrossRef]
- Isik, O.; Esselle, K.P. Backward wave microstrip lines with complementary spiral resonators. IEEE Trans. Antennas Propag. 2008, 56, 3173–3178. [Google Scholar] [CrossRef]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from conductors and enhanced nonlinear phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef] [Green Version]
- Falcone, F.; Lopetegi, T.; Baena, J.D.; Marqués, R.; Martín, F.; Sorolla, M. Effective negative-ε stopband microstrip lines based on complementary split ring resonators. IEEE Microw. Wirel. Components Lett. 2004, 14, 280–282. [Google Scholar] [CrossRef]
- Withayachumnankul, W.; Jaruwongrungsee, K.; Tuantranont, A.; Fumeaux, C.; Abbott, D. Metamaterial-based microfluidic sensor for dielectric characterization. Sensors Actuators, A Phys. 2013, 189, 233–237. [Google Scholar] [CrossRef] [Green Version]
- Abdolrazzaghi, M.; Zarifi, M.H.; Daneshmand, M. Sensitivity enhancement of split ring resonator based liquid sensors. Proc. IEEE Sensors 2017, 5–7. [Google Scholar] [CrossRef]
- Chuma, E.L.; Iano, Y.; Fontgalland, G.; Bravo Roger, L.L. Microwave sensor for liquid dielectric characterization based on metamaterial complementary split ring resonator. IEEE Sens. J. 2018, 18, 9978–9983. [Google Scholar] [CrossRef]
- Mohd Bahar, A.A.; Zakaria, Z.; Ab Rashid, S.R.; Isa, A.A.M.; Alahnomi, R.A. High-efficiency microwave planar resonator sensor based on bridge split ring topology. IEEE Microw. Wirel. Components Lett. 2017, 27, 545–547. [Google Scholar] [CrossRef]
- Zhang, X.; Ruan, C.; Ul Haq, T.; Chen, K. High-sensitivity microwave sensor for liquid characterization using a complementary circular spiral resonator. Sensors 2019, 19, 787. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boybay, M.S.; Ramahi, O.M. Non-destructive thickness measurement using quasi-static resonators. IEEE Microw. Wirel. Components Lett. 2013, 23, 217–219. [Google Scholar] [CrossRef]
- Lee, C.S.; Yang, C.L. Thickness and permittivity measurement in multi-layered dielectric structures using complementary split-ring resonators. IEEE Sens. J. 2014, 14, 695–700. [Google Scholar] [CrossRef]
- Lee, C.S.; Yang, C.L. Single compound complementary split-ring resonator for simultaneously measuring permittivity and thickness. IEEE MTT-S Int. Microw. Symp. Dig. 2014, 1–3. [Google Scholar] [CrossRef]
- Yang, C.L.; Lee, C.S.; Chen, K.W.; Chen, K.Z. Noncontact measurement of complex permittivity and thickness by using planar resonators. IEEE Trans. Microw. Theory Tech. 2016, 64, 247–257. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Khan, S.; Daneshmand, M. A Dual-Mode Split-Ring Resonator to Eliminate Relative Humidity Impact. IEEE Microw. Wirel. Components Lett. 2018, 28, 939–941. [Google Scholar] [CrossRef]
- Naqui, J.; Durán-Sindreu, M.; Martín, F. Novel sensors based on the symmetry properties of split ring resonators (SRRs). Sensors 2011, 11, 7545–7553. [Google Scholar] [CrossRef] [Green Version]
- Naqui, J.; Durán-Sindreu, M.; Martín, F. Alignment and position sensors based on split ring resonators. Sensors 2012, 12, 11790–11797. [Google Scholar] [CrossRef] [Green Version]
- Horestani, A.K.; Fumeaux, C.; Al-Sarawi, S.F.; Abbott, D. Displacement sensor based on diamond-shaped tapered split ring resonator. IEEE Sens. J. 2013, 13, 1153–1160. [Google Scholar] [CrossRef]
- Horestani, A.K.; Naqui, J.; Shaterian, Z.; Abbott, D.; Fumeaux, C.; Martín, F. Two-dimensional alignment and displacement sensor based on movable broadside-coupled split ring resonators. Sensors Actuators, A Phys. 2014, 210, 18–24. [Google Scholar]
- Horestani, A.K.; Naqui, J.; Abbott, D.; Fumeaux, C.; Martín, F. Two-dimensional displacement and alignment sensor based on reflection coefficients of open microstrip lines loaded with split ring resonators. Electron. Lett. 2014, 50, 620–622. [Google Scholar] [CrossRef] [Green Version]
- Naqui, J.; Martin, F. Transmission lines loaded with bisymmetric resonators and their application to angular displacement and velocity sensors. IEEE Trans. Microw. Theory Tech. 2013, 61, 4700–4713. [Google Scholar] [CrossRef]
- Horestani, A.K.; Abbott, D.; Fumeaux, C. Rotation sensor based on horn-shaped split ring resonator. IEEE Sens. J. 2013, 13, 3014–3015. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.F.; Abbott, D. Metamaterial-inspired rotation sensor with wide dynamic range. IEEE Sens. J. 2014, 14, 2609–2614. [Google Scholar] [CrossRef]
- Mata-Contreras, J.; Herrojo, C.; Martin, F. Application of Split Ring Resonator (SRR) Loaded Transmission Lines to the Design of Angular Displacement and Velocity Sensors for Space Applications. IEEE Trans. Microw. Theory Tech. 2017, 65, 4450–4460. [Google Scholar] [CrossRef] [Green Version]
- Melik, R.; Unal, E.; Perkgoz, N.K.; Puttlitz, C.; Demir, H.V. Metamaterial-based wireless strain sensors. Appl. Phys. Lett. 2009, 95, 1–3. [Google Scholar] [CrossRef]
- Hasani, M.; Vena, A.; Sydanheimo, L.; Ukkonen, L.; Tentzeris, M.M. Implementation of a dual-interrogation-mode embroidered RFID-Enabled strain sensor. IEEE Antennas Wirel. Propag. Lett. 2013, 12, 1272–1275. [Google Scholar] [CrossRef]
- Thai, T.T.; Aubert, H.; Pons, P.; Dejean, G.; Mtentzeris, M.; Plana, R. Novel design of a highly sensitive RF strain transducer for passive and remote sensing in two dimensions. IEEE Trans. Microw. Theory Tech. 2013, 61, 1385–1396. [Google Scholar] [CrossRef]
- Muhammed Shafi, K.T.; Ansari, M.A.H.; Jha, A.K.; Akhtar, M.J. Design of SRR-based microwave sensor for characterization of magnetodielectric substrates. IEEE Microw. Wirel. Components Lett. 2017, 27, 524–526. [Google Scholar]
- Muhammed Shafi, K.T.; Jha, A.K.; Akhtar, M.J. Improved Planar Resonant RF Sensor for Retrieval of Permittivity and Permeability of Materials. IEEE Sens. J. 2017, 17, 5479–5486. [Google Scholar] [CrossRef]
- Saadat-safa, M.; Nayyeri, V.; Member, S.; Khanjarian, M.; Soleimani, M.; Ramahi, O.M. A CSRR-Based Sensor for Full Characterization of Magneto-Dielectric Materials. IEEE Trans. Microw. Theory Tech. 2019, 67, 806–814. [Google Scholar] [CrossRef]
- Velez, P.; Su, L.; Grenier, K.; Mata-Contreras, J.; Dubuc, D.; Martin, F. Microwave Microfluidic Sensor Based on a Microstrip Splitter/Combiner Configuration and Split Ring Resonators (SRRs) for Dielectric Characterization of Liquids. IEEE Sens. J. 2017, 17, 6589–6598. [Google Scholar] [CrossRef] [Green Version]
- Su, L.; Mata-Contreras, J.; Vélez, P.; Martín, F. Configurations of splitter/combiner microstrip sections loaded with stepped impedance resonators (SIRs) for sensing applications. Sensors 2016, 16, 2195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Su, L.; Mata-Contreras, J.; Velez, P.; Martin, F. Splitter/combiner microstrip sections loaded with pairs of Complementary Split Ring Resonators (CSRRs): Modeling and optimization for differential sensing applications. IEEE Trans. Microw. Theory Tech. 2016, 64, 4362–4370. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Differential sensors using microstrip lines loaded with two split-ring resonators. IEEE Sens. J. 2018, 18, 5786–5793. [Google Scholar] [CrossRef]
- Naqui, J.; Damm, C.; Wiens, A.; Jakoby, R.; Su, L.; Mata-Contreras, J.; Martín, F. Transmission Lines Loaded With Pairs of Stepped Impedance Resonators: Modeling and Application to Differential Permittivity Measurements. IEEE Trans. Microw. Theory Tech. 2016, 64, 3864–3877. [Google Scholar] [CrossRef] [Green Version]
- Haq, T.; Ruan, C.; Ullah, S.; Kosar Fahad, A. Dual notch microwave sensors based on complementary metamaterial resonators. IEEE Access 2019, 7, 153489–153498. [Google Scholar] [CrossRef]
- Boybay, M.S.; Ramahi, O.M. Material characterization using complementary split-ring resonators. IEEE Trans. Instrum. Meas. 2012, 61, 3039–3046. [Google Scholar] [CrossRef]
- Lee, C.S.; Yang, C.L. Complementary split-ring resonators for measuring dielectric constants and loss tangents. IEEE Microw. Wirel. Components Lett. 2014, 24, 563–565. [Google Scholar] [CrossRef]
- Lee, C.S.; Yang, C.L. Single-compound complementary split-ring resonator for simultaneously measuring the permittivity and thickness of dual-layer dielectric materials. IEEE Trans. Microw. Theory Tech. 2015, 63, 2010–2023. [Google Scholar] [CrossRef]
- Ansari, M.A.H.; Jha, A.K.; Akhtar, M.J. Design and Application of the CSRR-Based Planar Sensor for Noninvasive Measurement of Complex Permittivity. IEEE Sens. J. 2015, 15, 7181–7189. [Google Scholar] [CrossRef]
- Florencio Díaz, R.; Rodríguez Boix, R.; Carrasco Yépez, F.; Encinar Garcinuño, J.; Barba Gea, M.; Pérez Palomino, G. Broadband reflectarrays made of cells with three coplanar parallel dipoles. Microw. Opt. Technol. Lett. 2014, 56, 748–753. [Google Scholar] [CrossRef]
- Alotaibi, S.A.; Cui, Y.; Tentzeris, M.M. CSRR Based Sensors for Relative Permittivity Measurement with Improved and Uniform Sensitivity throughout [0.9-10.9] GHz Band. IEEE Sens. J. 2019, 1–12. [Google Scholar] [CrossRef]
- Langlois, S.; Lit, J.W.Y. S-resonator with an end reflector. J. Light. Technol. 1999, 17, 1487–1492. [Google Scholar] [CrossRef]
- Deleniv, A.; Gashinova, M.; Eriksson, A.; Khalabuhov, A. Novel band-pass filter utilizing S-shaped slot line resonators. IEEE MTT-S Int. Microw. Symp. Dig. 2003, 2, 1081–1084. [Google Scholar]
- Chen, F.C.; Chu, Q.X. A compact dual-band filter using S-shaped stepped impedance resonators. 2008 Int. Conf. Microw. Millim. Wave Technol. Proceedings, ICMMT 2008, 3, 1255–1257. [Google Scholar]
- Suntheralingam, N.; Budimir, D. Compact S-shaped resonator loaded waveguide bandpass filters. IEEE Antennas Propag. Soc. AP-S Int. Symp. 2009, 1–4. [Google Scholar]
- Khan, M.F.; Mughal, M.J. Tunable metamaterials by varying the inductance and capacitance of S-shaped resonator. In Proceedings of the 2009 3rd IEEE International Symposium on Microwave, Antenna, Propagation and EMC Technologies for Wireless Communications, Beijing, China, 27–29 October 2009; pp. 140–143. [Google Scholar]
- Herrojo, C.; Mata-Contreras, J.; Paredes, F.; Martín, F. Microwave Encoders for Chipless RFID and Angular Velocity Sensors Based on S-Shaped Split Ring Resonators. IEEE Sens. J. 2017, 17, 4805–4813. [Google Scholar] [CrossRef] [Green Version]
- Bonache, J.; Gil, M.; Gil, I.; García-García, J.; Martín, F. On the electrical characteristics of complementary metamaterial resonators. IEEE Microw. Wirel. Components Lett. 2006, 16, 543–545. [Google Scholar] [CrossRef]
- Haq, T.; Ruan, C.; Zhang, X.; Kosar, A.; Ullah, S. Low cost and compact wideband microwave notch filter based on miniaturized complementary metaresonator. Appl. Phys. A Mater. Sci. Process. 2019, 125, 1–7. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; ISBN 9789896540821. [Google Scholar]
- Haq, T.U.; Ruan, C.; Zhang, X.; Ullah, S. Complementary Metamaterial Sensor for Nondestructive Evaluation of Dielectric Substrates. Sensors 2019, 19, 2100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ebrahimi, A.; Scott, J.; Ghorbani, K. Ultrahigh-Sensitivity Microwave Sensor for Microfluidic Complex Permittivity Measurement. IEEE Trans. Microw. Theory Tech. 2019, 67, 4269–4277. [Google Scholar] [CrossRef]
- Ebrahimi, A.; Withayachumnankul, W.; Al-Sarawi, S.; Aboott, D. High-Sensitivity Metamaterial-Inspired Sensor. IEEE Sens. J. 2014, 14, 1345–1351. [Google Scholar] [CrossRef] [Green Version]
- Rowe, D.J.; Abduljabar, A.A.; Porch, A.; Barrow, D.A.; Allender, C.J. Improved Split-Ring Resonator for Micro Fluidic Sensing. IEEE Trans. Microw. Theory Tech. 2014, 62, 689–700. [Google Scholar] [CrossRef]
- Abdolrazzaghi, M.; Daneshmand, M.; Iyer, A.K. Strongly Enhanced Sensitivity in Planar Microwave Sensors Based on Metamaterial Coupling. IEEE Trans. Microw. Theory Tech. 2018, 66, 1843–1855. [Google Scholar] [CrossRef] [Green Version]
- Galindo-Romera, G.; Javier Herraiz-Martínez, F.; Gil, M.; Martínez-Martínez, J.J.; Segovia-Vargas, D. Submersible Printed Split-Ring Resonator-Based Sensor for Thin-Film Detection and Permittivity Characterization. IEEE Sens. J. 2016, 16, 3587–3596. [Google Scholar] [CrossRef]
- Su, L.; Mata-Contreras, J.; Vélez, P.; Fernández-Prieto, A.; Martín, F. Analytical method to estimate the complex permittivity of oil samples. Sensors 2018, 18, 984. [Google Scholar] [CrossRef] [Green Version]



| Ref | Hosting Transmission Line | Resonating Structure | Frequency Band (GHz) | Shift in Resonance Frequency |
|---|---|---|---|---|
| [49] | Microstrip | Rectangular CSRR | 0.8–1.3 | 38% |
| [50] | Microstrip | Rectangular CSRR | 1.8–2.8 | 36% |
| [51] | Microstrip | Single Compound CSRR | 1.08–1.63 | 34% |
| [52] | Microstrip | Circular CSRR | 1.75–2.75 | 36% |
| [53] | Microstrip | Hexagonal CSRR | 5.23–8.45 | 38% |
| [54] | Microstrip | Single CSRR | 0.90–10.90 | 50% |
| This Work | Microstrip | CSSSR | 13.28–15.17 | 100% |
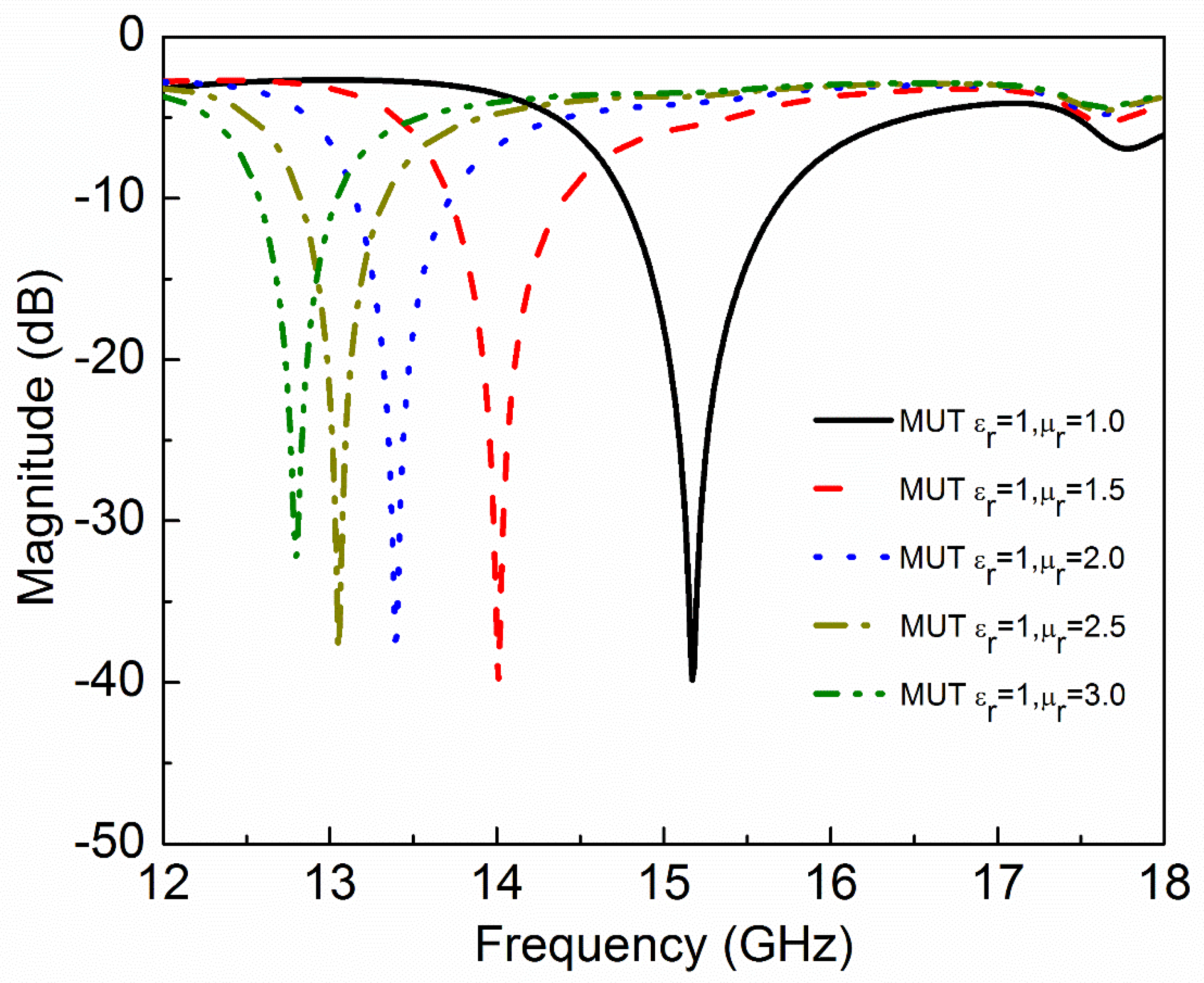
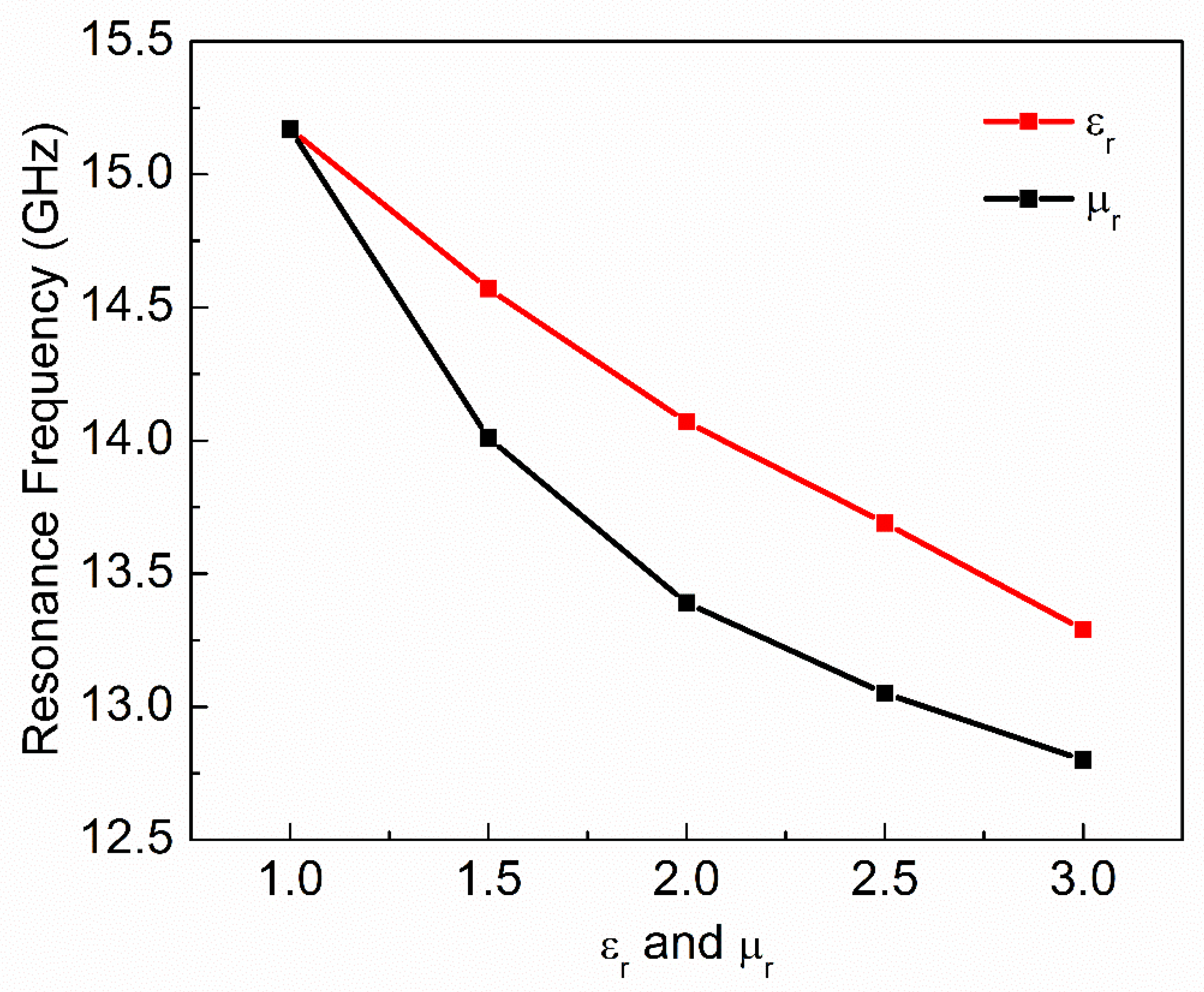
| Material Under Test (MUT) | Resonance Frequency | Notch Depth | |||
|---|---|---|---|---|---|
| εr | µr | tanδe | tanδm | GHz | dB |
| 1.0 | 1 | 0 | 0 | 15.17 | −39.84 |
| 1.5 | 1 | 0 | 0 | 14.57 | −44.88 |
| 2.0 | 1 | 0 | 0 | 14.07 | −38.41 |
| 2.5 | 1 | 0 | 0 | 13.69 | −40.77 |
| 3.0 | 1 | 0 | 0 | 13.29 | −42.32 |
| Material Under Test (MUT) | Resonance Frequency | Notch Depth | |||
|---|---|---|---|---|---|
| εr | µr | tanδe | tanδm | GHz | dB |
| 1 | 1.0 | 0 | 0 | 15.17 | −39.84 |
| 1 | 1.5 | 0 | 0 | 14.01 | −40.11 |
| 1 | 2.0 | 0 | 0 | 13.39 | −37.41 |
| 1 | 2.5 | 0 | 0 | 13.05 | −37.93 |
| 1 | 3.0 | 0 | 0 | 12.80 | −32.23 |
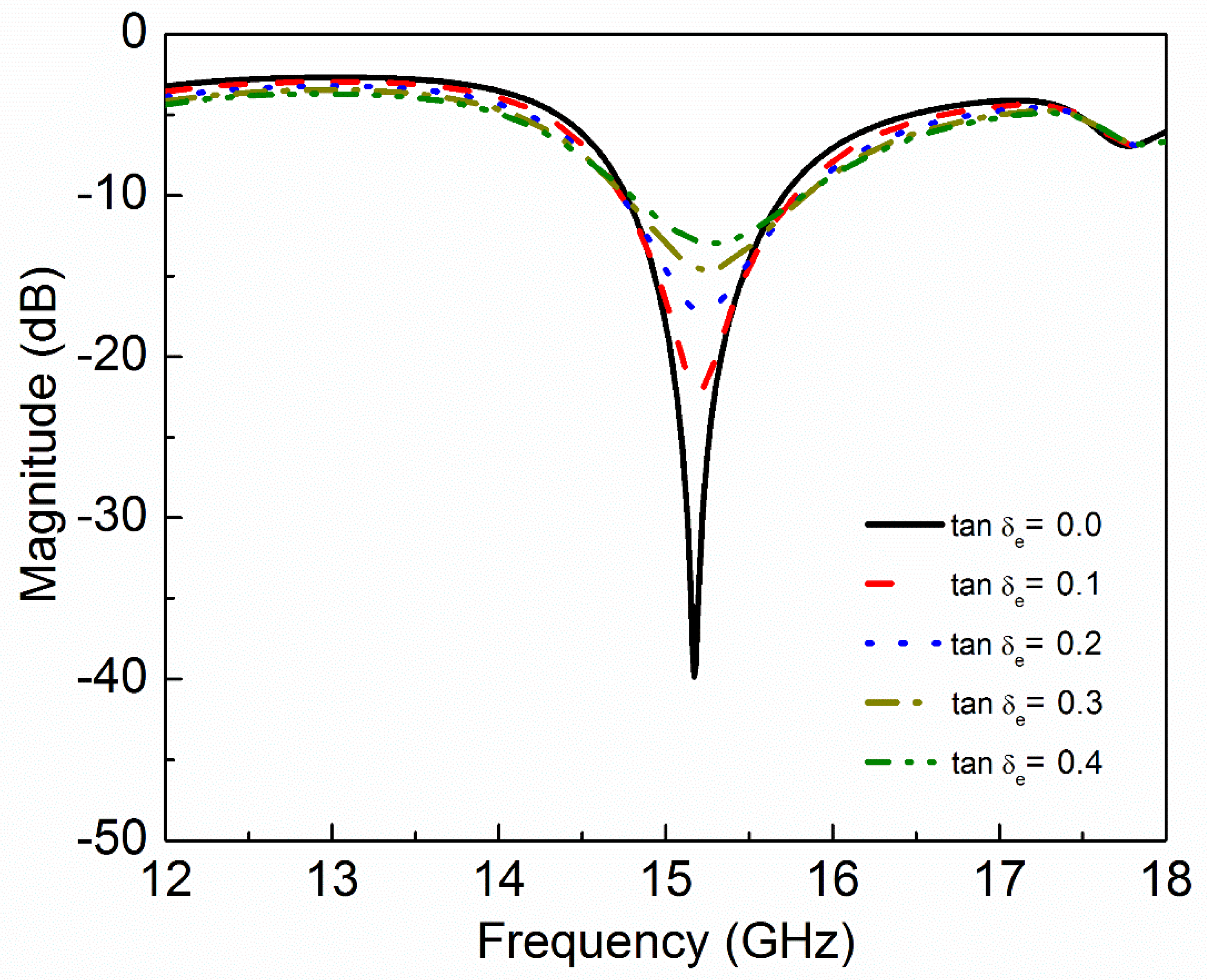
| Material Under Test (MUT) | Resonance Frequency | Notch Depth | |||
|---|---|---|---|---|---|
| εr | µr | tanδe | tanδm | GHz | dB |
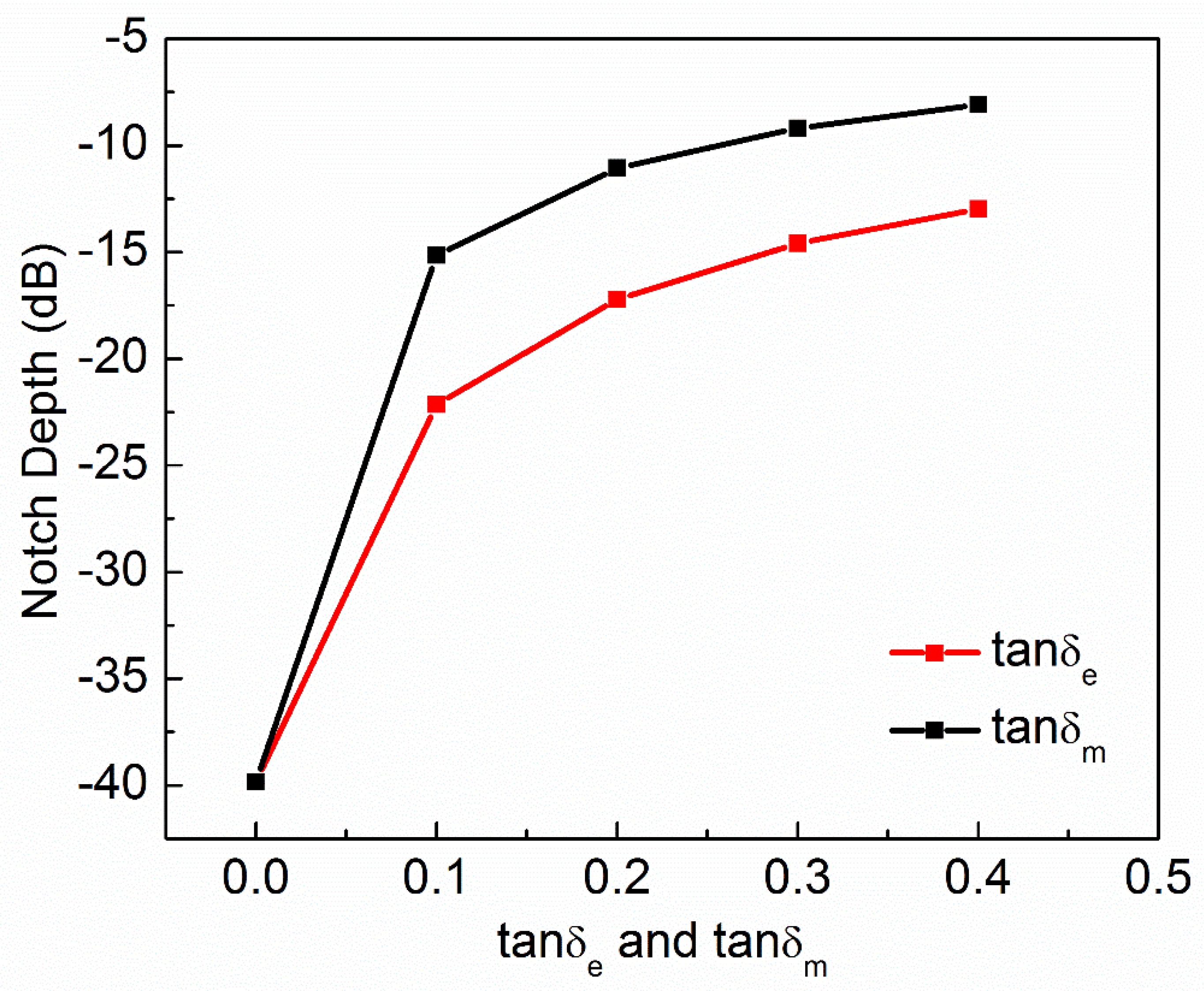
| 1 | 1 | 0.0 | 0 | 15.17 | −39.84 |
| 1 | 1 | 0.1 | 0 | 15.20 | −22.15 |
| 1 | 1 | 0.2 | 0 | 15.22 | −17.21 |
| 1 | 1 | 0.3 | 0 | 15.25 | −14.60 |
| 1 | 1 | 0.4 | 0 | 15.28 | −12.96 |
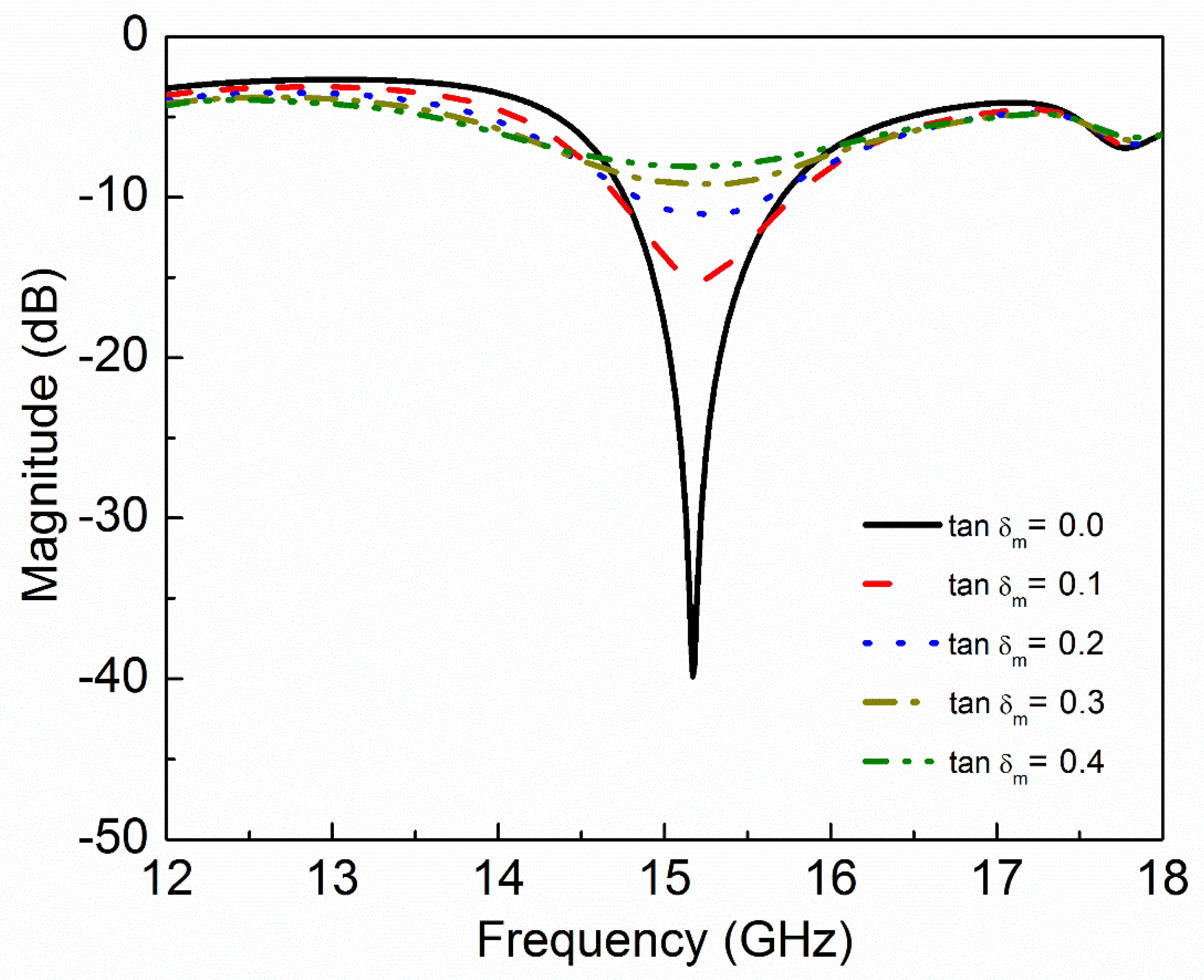
| Material Under Test (MUT) | Resonance Frequency | Notch Depth | |||
|---|---|---|---|---|---|
| εr | µr | tanδe | tanδm | GHz | dB |
| 1 | 1 | 0 | 0.0 | 15.17 | −39.84 |
| 1 | 1 | 0 | 0.1 | 15.21 | −15.15 |
| 1 | 1 | 0 | 0.2 | 15.28 | −11.06 |
| 1 | 1 | 0 | 0.3 | 15.32 | −9.19 |
| 1 | 1 | 0 | 0.4 | 15.30 | −8.08 |
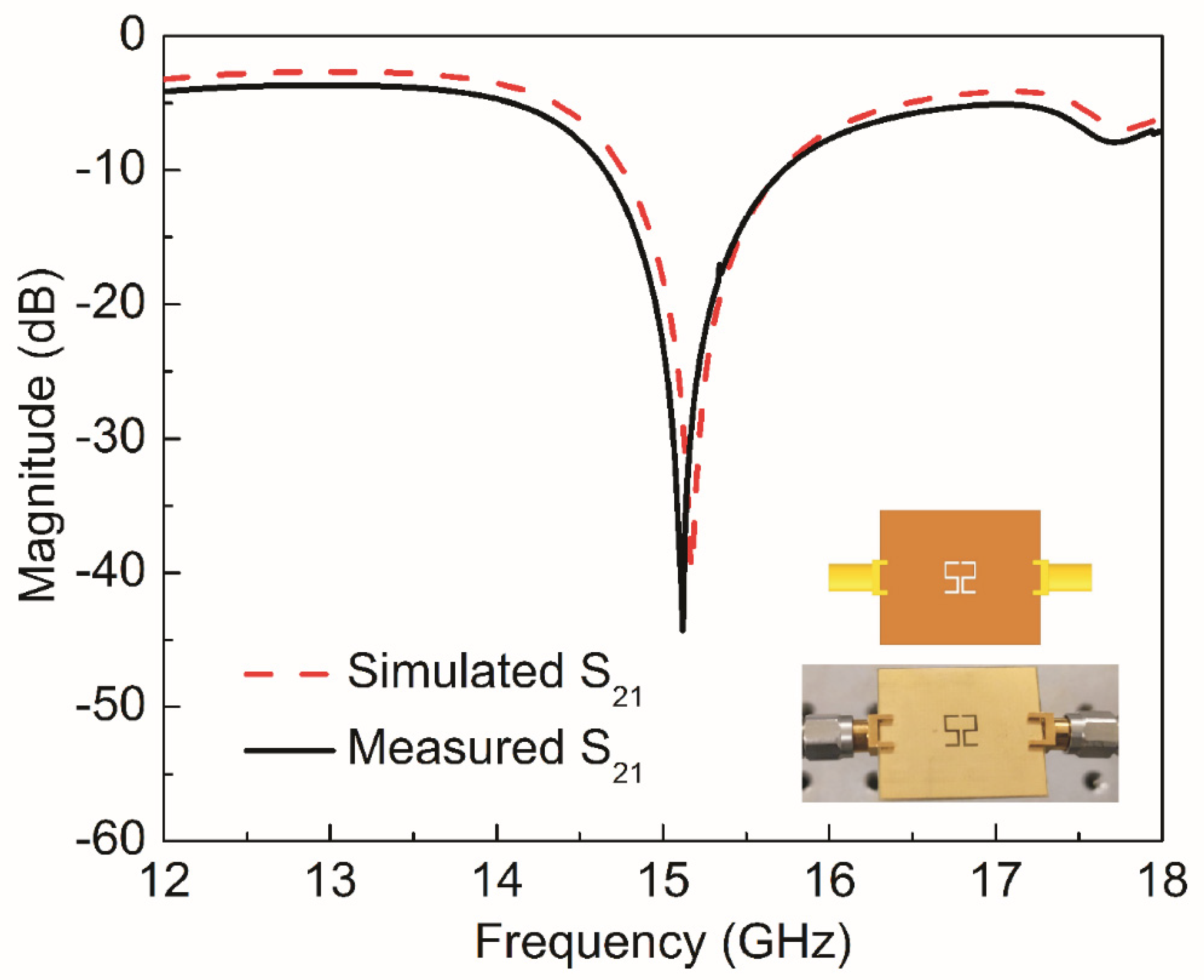
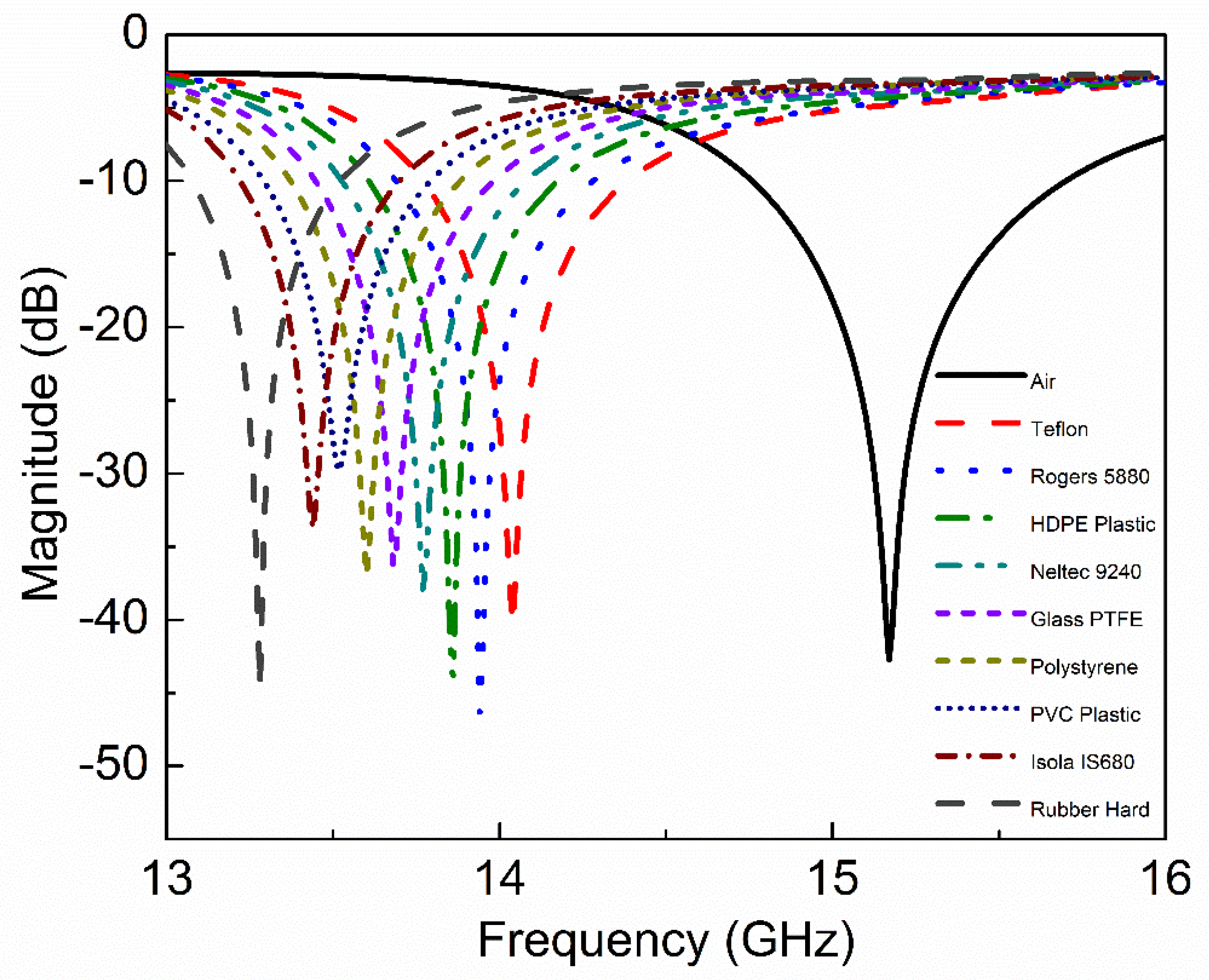
| Material Under Test (MUT) | MUT Properties | Simulated Resonance Frequency | Measured Resonance Frequency | |||
|---|---|---|---|---|---|---|
| εr | µr | tanδe | tanδm | GHz | GHz | |
| Teflon(tm) | 2.1 | 1 | 0.001 | 0 | 14.04 | 13.99 |
| Rogers RT5880 | 2.2 | 1 | 0.0009 | 0 | 13.95 | 13.89 |
| HDPE Plastic | 2.3 | 1 | 0.0005 | 0 | 13.86 | 13.80 |
| Neltec NX9240 | 2.4 | 1 | 0.0016 | 13.77 | 13.72 | |
| Glass PTFEreinf | 2.5 | 1 | 0.002 | 0 | 13.68 | 13.63 |
| Polystyrene | 2.6 | 1 | 0 | 0 | 13.60 | 13.55 |
| PVC Plastic | 2.7 | 1 | 0.007 | 0 | 13.52 | 13.46 |
| Isola IS680-280 | 2.8 | 1 | 0.0025 | 0 | 13.44 | 13.38 |
| Rubber Hard | 3 | 1 | 0 | 0 | 13.28 | 13.23 |
| Material Under Test (MUT) | Differential Input | Differential Output | Differential Sensitivity |
|---|---|---|---|
| % | |||
| Teflon(tm) | 1.0994 | 1.13 | 102 |
| Rogers RT5880 | 1.1994 | 1.23 | 102 |
| HDPE Plastic | 1.2994 | 1.32 | 101 |
| Netltec NX9240 | 1.3994 | 1.40 | 100 |
| Glass PTFEreinf | 1.4994 | 1.49 | 99 |
| Polystyrene | 1.5994 | 1.57 | 98 |
| PVC Plastic | 1.6994 | 1.66 | 98 |
| Isola IS680-280 | 1.7994 | 1.74 | 97 |
| Rubber Hard | 1.9994 | 1.89 | 95 |
| Ref | Resonating Structure | Resonance Frequency (GHz) | Permittivity Range Studied | Relative Sensitivity (%) |
|---|---|---|---|---|
| [65] | SIR | 1.91 | 10–80 | 0.84 |
| [66] | CSRR | 2.4 | 10–80 | 0.61 |
| [67] | SRR | 1.72 | 10–80 | 0.78 |
| [68] | Open-Loop Resonators | 2.6 | 10–140 | 1.49 |
| [69] | SRR | 1.8 | 2.42–22.52 | 3.04 |
| [70] | CSRR | 2.5 | 2.93–3.64 | 3.58 |
| This Work | CSSSR | 15.12 | 2.1–3 | 6.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haq, T.; Ruan, C.; Zhang, X.; Ullah, S.; Fahad, A.K.; He, W. Extremely Sensitive Microwave Sensor for Evaluation of Dielectric Characteristics of Low-Permittivity Materials. Sensors 2020, 20, 1916. https://doi.org/10.3390/s20071916
Haq T, Ruan C, Zhang X, Ullah S, Fahad AK, He W. Extremely Sensitive Microwave Sensor for Evaluation of Dielectric Characteristics of Low-Permittivity Materials. Sensors. 2020; 20(7):1916. https://doi.org/10.3390/s20071916
Chicago/Turabian StyleHaq, Tanveerul, Cunjun Ruan, Xingyun Zhang, Shahid Ullah, Ayesha Kosar Fahad, and Wenlong He. 2020. "Extremely Sensitive Microwave Sensor for Evaluation of Dielectric Characteristics of Low-Permittivity Materials" Sensors 20, no. 7: 1916. https://doi.org/10.3390/s20071916
APA StyleHaq, T., Ruan, C., Zhang, X., Ullah, S., Fahad, A. K., & He, W. (2020). Extremely Sensitive Microwave Sensor for Evaluation of Dielectric Characteristics of Low-Permittivity Materials. Sensors, 20(7), 1916. https://doi.org/10.3390/s20071916






