On a Sensor Placement Methodology for Monitoring the Vibrations of Horizontally Excited Ground
Abstract
:1. Introduction: The Importance of the Analysed Problem
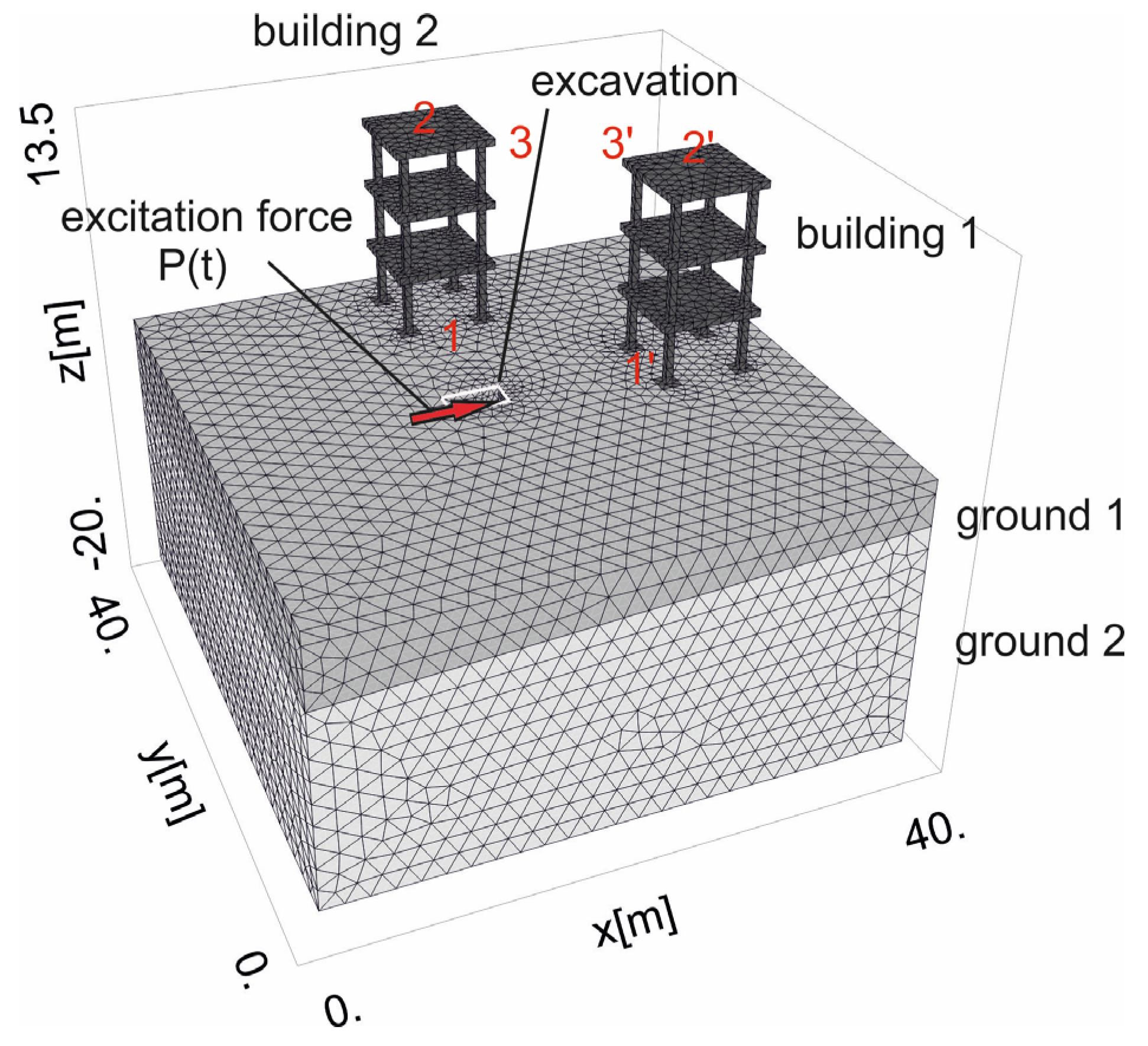
2. Mathematical and Numerical Models
3. Soil Characteristics
4. Results and Discussion
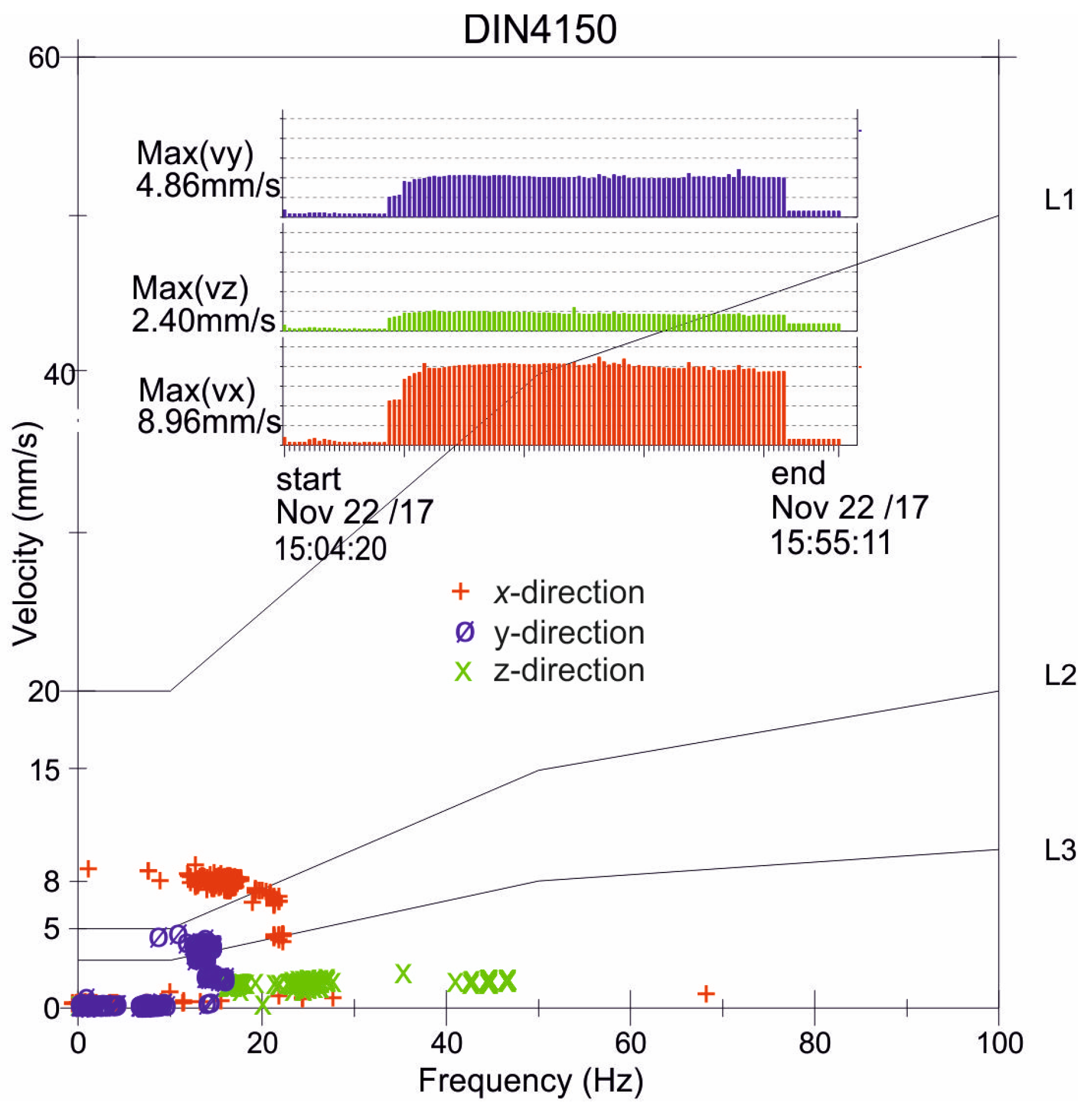
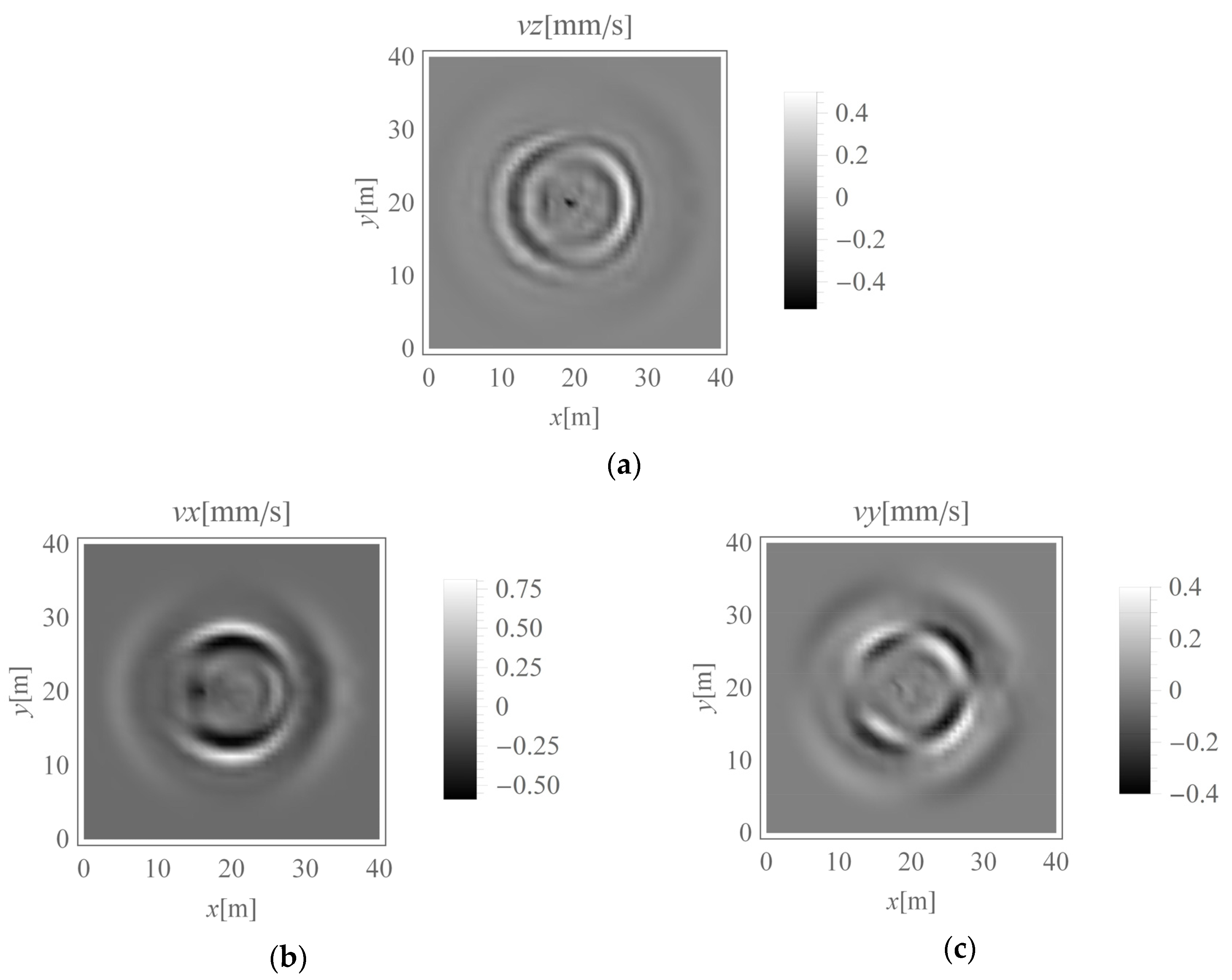
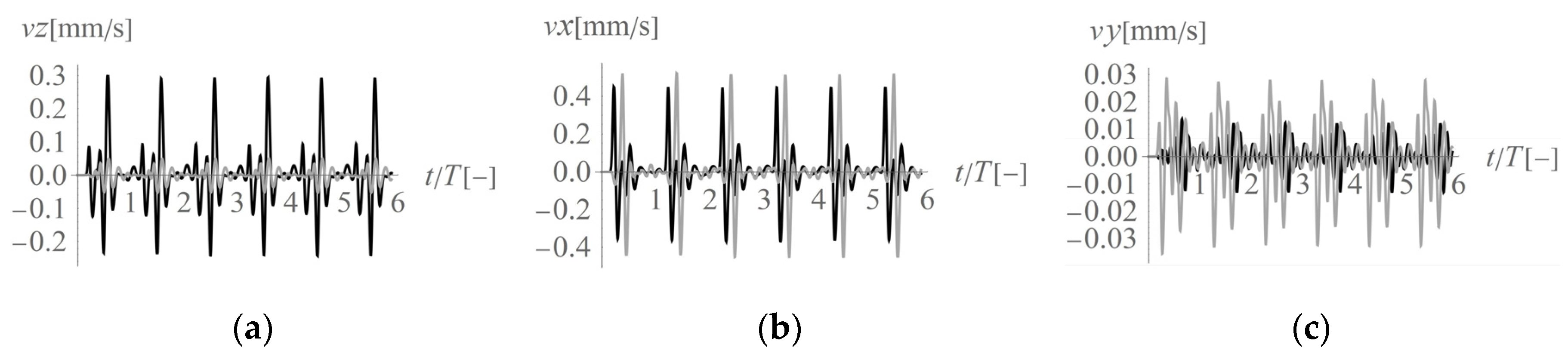
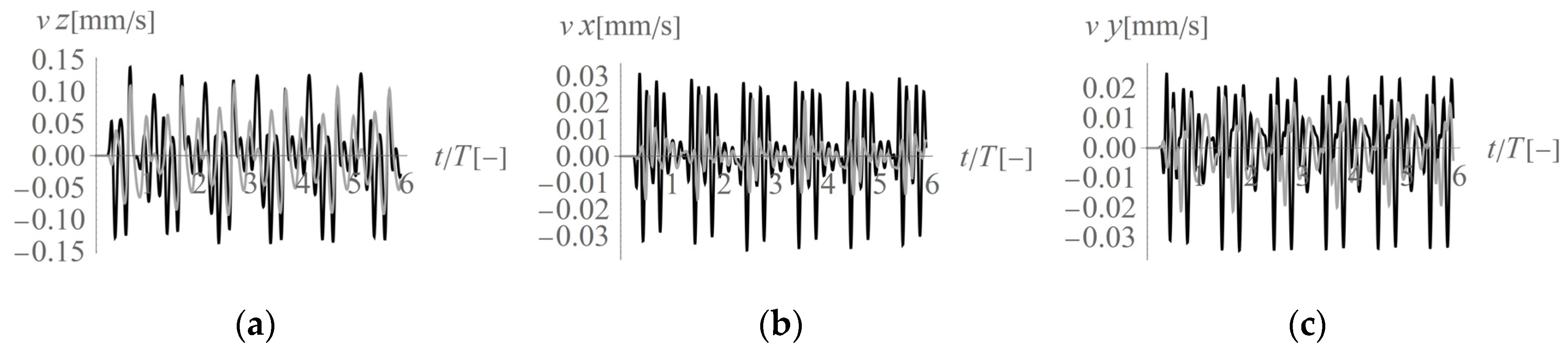
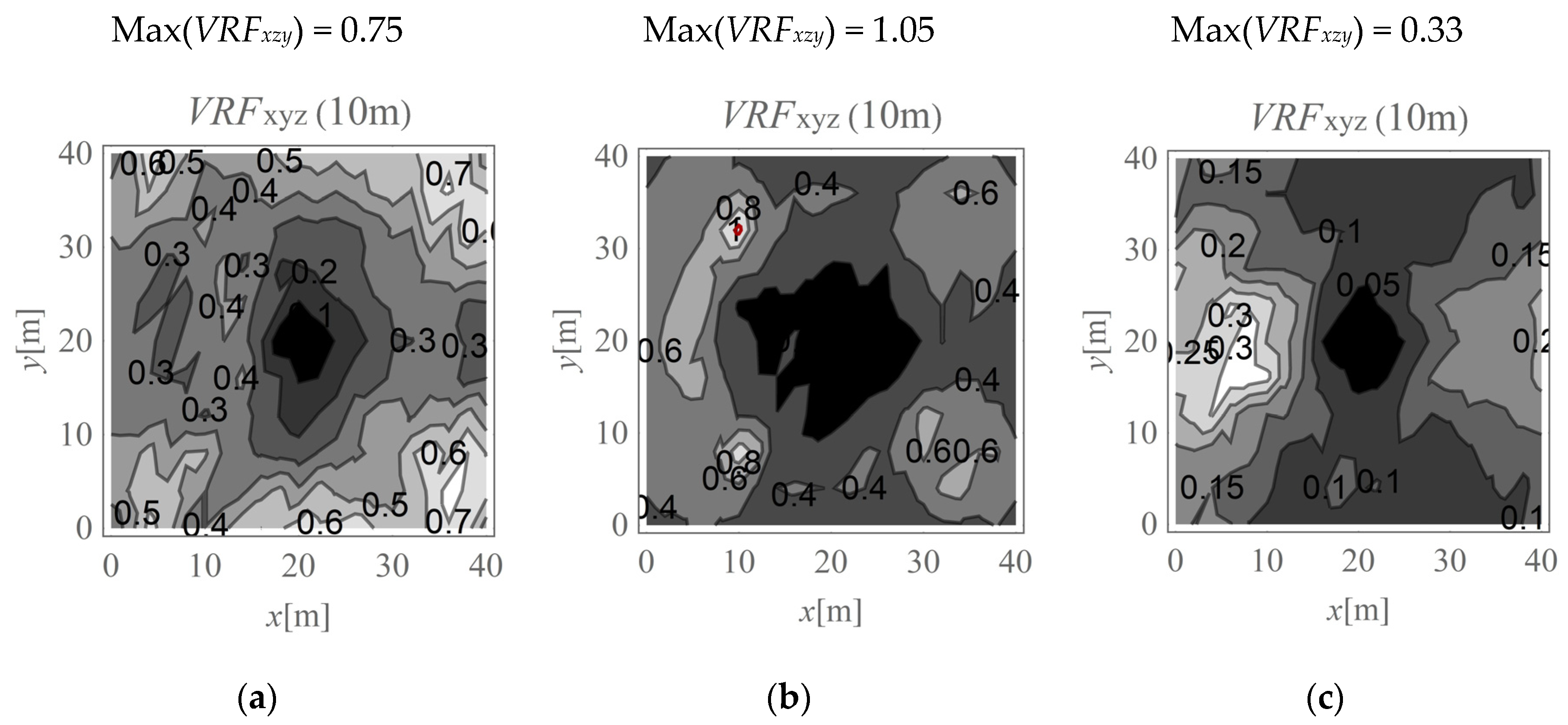
4.1. The Maximum Soil Response Measured on the Ground Surface
4.2. The Maximum Soil Response Measured below the Ground Surface
5. Summary: Recommendations for Sensor Placement for the Vibration Monitoring of Structures
5.1. For Structures Located on the Ground Surface
- The maximal soil response is observed in the direction perpendicular to the direction of the applied force. Therefore, special attention should be paid to monitoring structures that lie on the line from the vibration source and in a direction perpendicular to the direction of excitation. Sensors should be located in this area.
- In the case of ceilings and rooves sensitive to dynamic loads, more attention should be paid to structures located in front of the excitation force (building 1), where much greater values (by approximately five times) of the vertical velocity components are generally measured compared to those in the opposite direction (building 2). In such a case, sensors should be located in the middle of the highest floor of a building located in front of the applied force to predict the largest dynamic response of the structural element.
- The closer the distance between the vibration source and structure is, the greater the measured value of the soil response. Sensors should be placed on the structural element (e.g., a wall or foundation) that is located closest to the vibration source.
5.2. For Underground Structures
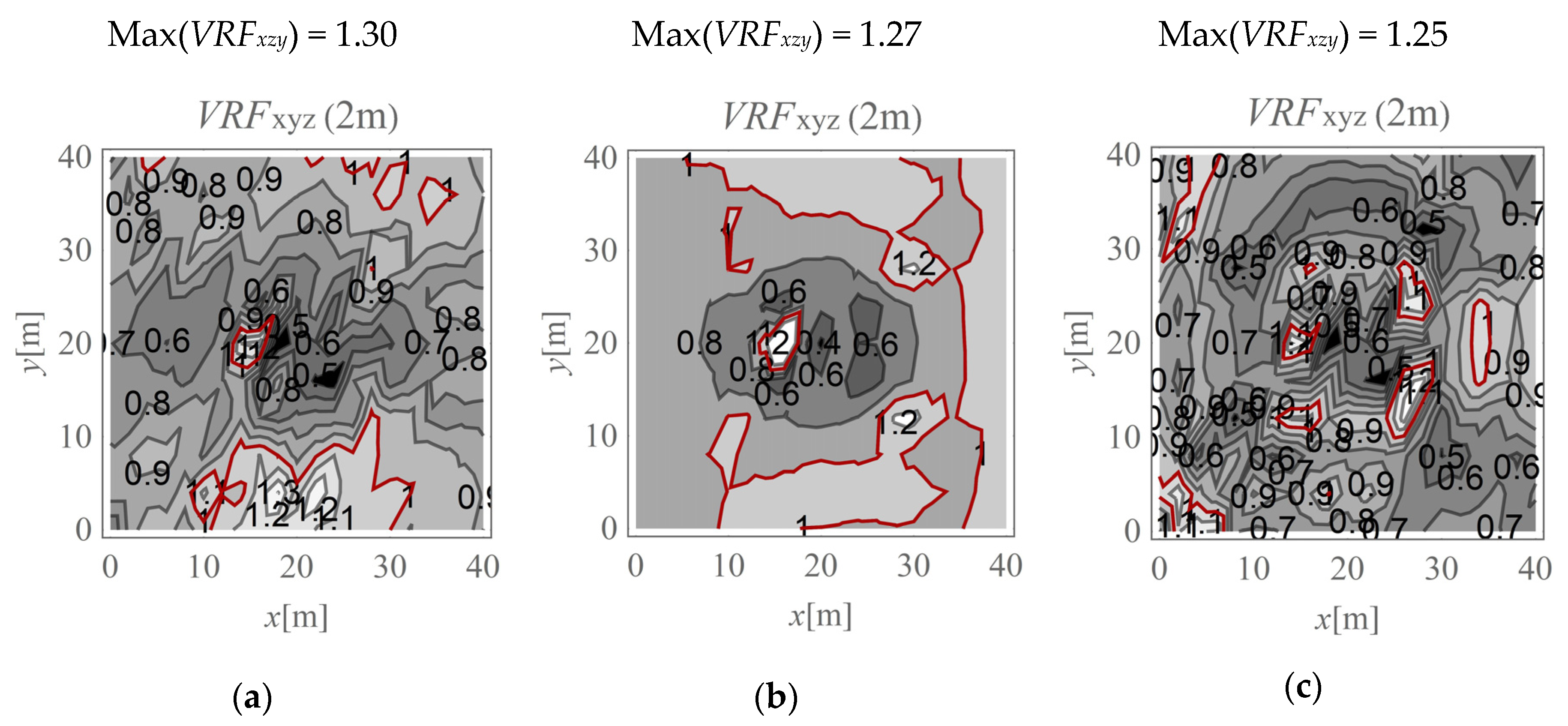
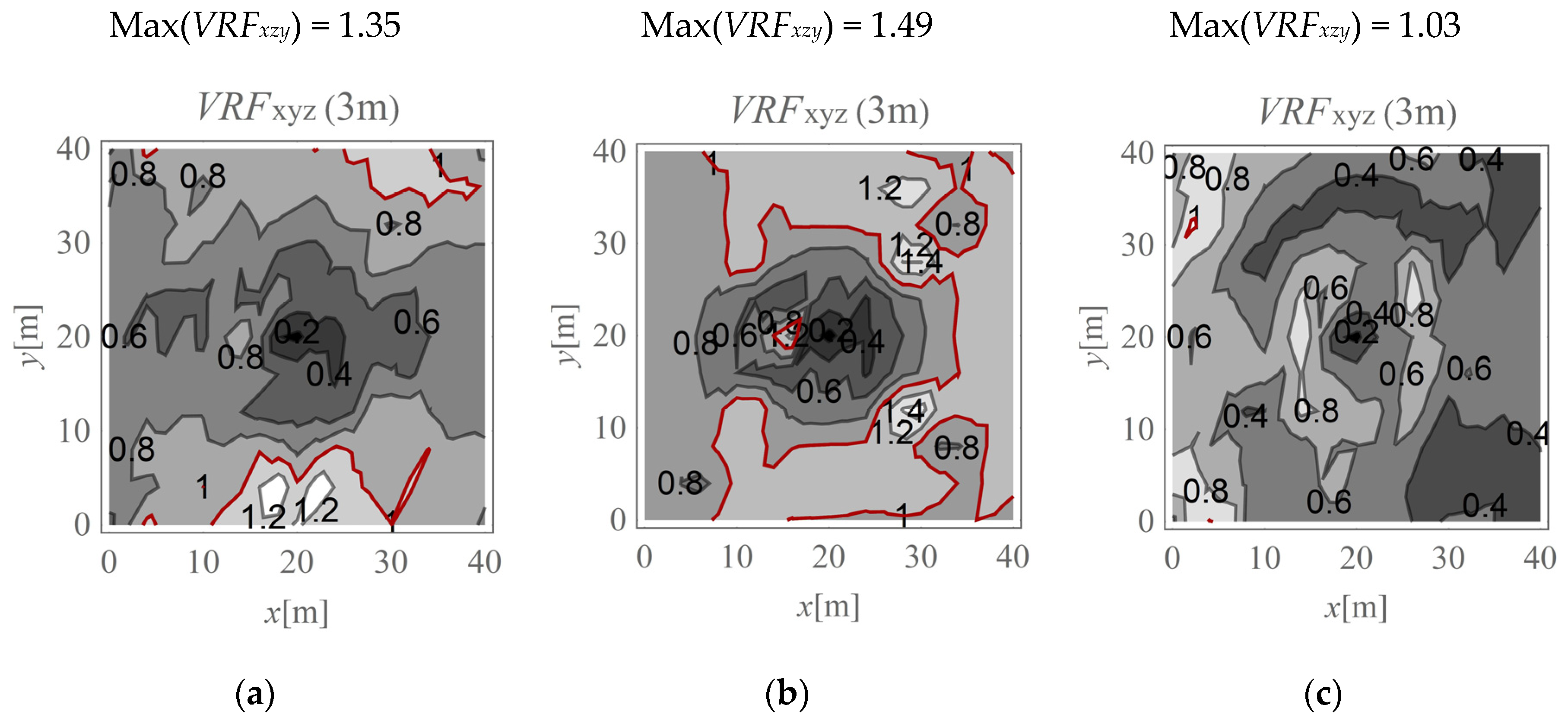
- Special attention should be paid to cases in vibration monitoring when a “strong” soil deposit (e.g., dense sand, gravel) overlies a “weaker” one (e.g., silt, loam). For such subsoil conditions, the maximal soil response (PPV) below the ground surface can be ≈50% greater than the corresponding value measured on the ground surface. This effect is more significant in the region in front of the applied load and when the boundary surface between the two layers is located close to the ground surface. During vibration monitoring of underground structures in these soil conditions, special attention should be paid to the area in front of the applied load. When vibration monitoring is based on measurements made directly on the ground surface, the recorded values should be increased by approximately 50% compared with the threshold values. This approach can help to avoid underestimations of the structure’s damage risk.
- For homogenous ground conditions, the amplification of velocity amplitudes may also occur below the ground surface, but the effect is less visible compared to that in the case described above (a “strong” soil deposit overlies a “weaker” one). A practical conclusion is that for homogenous ground conditions, when the vibration monitoring of underground structures is based on measurements made directly on the ground surface, the recorded velocity amplitudes should be increased by approximately 40% compared with the threshold values. This issue is especially important for points located in the direction perpendicular to the direction of the force.
- The largest vibration amplification appears in the case when a “strong” soil deposit overlies a “weaker” one. The opposite soil layering (“weaker” soil layer located close to the ground surface) can also result in vibration amplification; however, the effect is less visible compared to that for homogeneous ground conditions and the case with the opposite layering. In the case of a “weaker” soil layer located close to the ground surface, vibration monitoring can be based on sensors located on the ground surface; however, before comparing recorded vibration amplitudes with threshold values, the recorded values should be increased by approximately 25% to avoid underestimations of the structure’s damage risk.
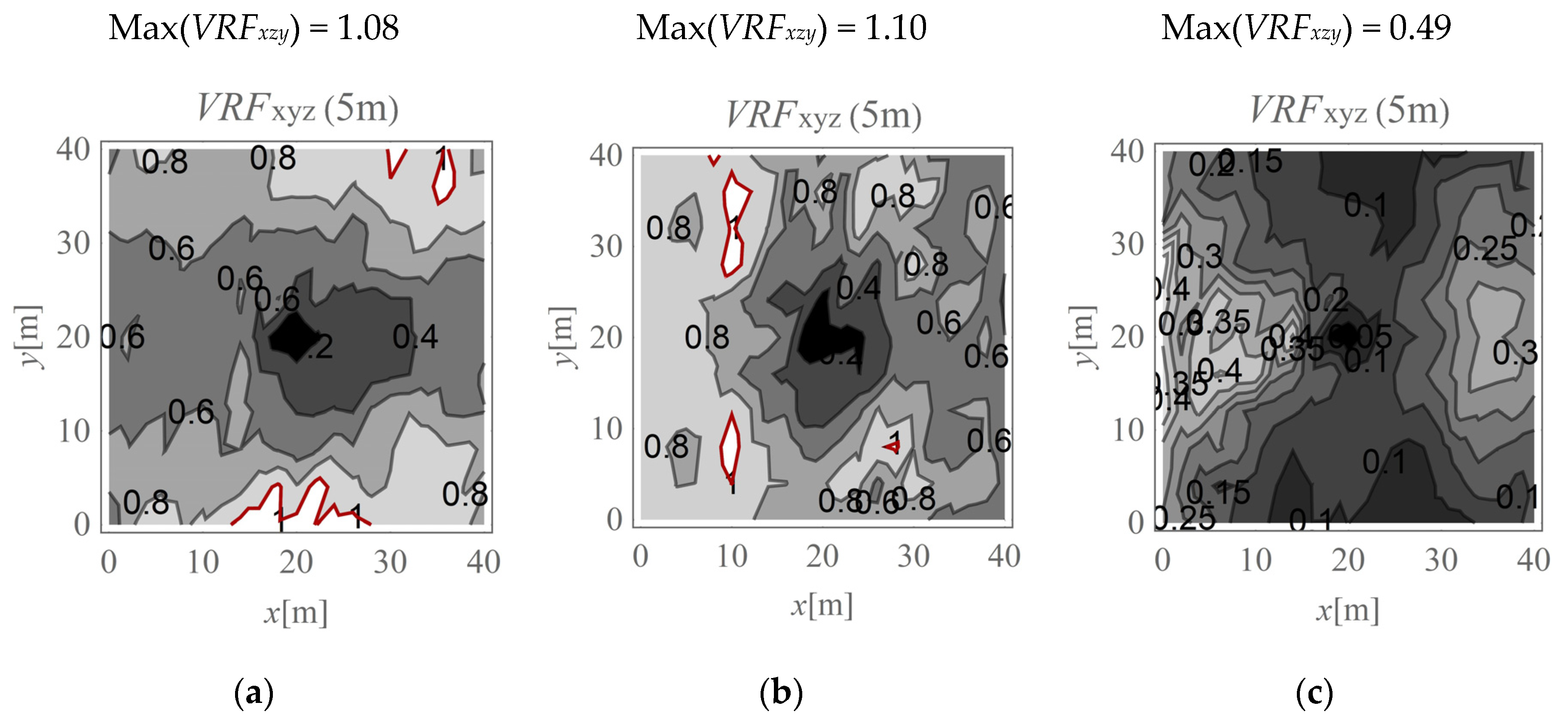
- The effect of vibration amplification can be observed to a depth of approximately 5 m. For points located deeper than 5 m, the velocity component values measured at the ground surface will generally be greater than those measured at the selected depths. Therefore, the vibration monitoring of underground structures located deeper than 5 m below the ground surface can be based on the measurements obtained by sensors located directly on the ground surface. The safety of a structure can be ensured with this approach.
- The largest differences between the soil responses measured below and on the ground surface appear at depths of 2–3 m for homogeneous ground conditions. For heterogeneous ground conditions, the largest amplifications can be observed deeper (3–4 m below the ground level), near where the interface between two layers appears. Therefore, the vibration monitoring of underground structures located at the mentioned depths (2–4 m) is particularly important.
- Obviously, the shorter the distance between the excitation force and an underground structure, the greater the measured velocities. Sensors should be located on or above the underground structure and as close as possible to the vibration source.
6. Conclusions
- Special attention should focus on the vibration monitoring of underground structures, which is usually based on measurements from sensors located directly on the ground surface. In such cases, the maximal values of the velocities that appear below the ground surface can be as much as 50% greater than those recorded on the ground surface. This effect is most significant in the case when a “strong” soil deposit overlies a “weaker” deposit and in the area located in front of the applied load. Before comparing the values measured on the ground surface with threshold values related to underground structures given by codes and standards, the recorded values should be increased. Thus, the risk of structural damage will not be underestimated.
- In the case of structures located at the ground surface, the largest soil response appears in the direction perpendicular to the excitation force direction (building 2). During the vibration monitoring of structures, focus should be placed on monitoring in this area. Notably, the shorter the distance to the vibration source is, the more significant the soil/structure response to dynamic excitation will be.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Liu, X.; Lu, Z.; Yang, W.; Huang, M.; Tong, X. Dynamic Monitoring and Vibration Analysis of Ancient Bridges by Ground-Based Microwave Interferometry and the ESMD Method. Remote Sens. 2018, 10, 770. [Google Scholar] [CrossRef] [Green Version]
- Nedoma, J.; Stolarik, M.; Kepak, S.; Pinka, M.; Martinek, R.; Frnda, J.; Fridrich, M. Alternative Approaches to Measurement of Ground Vibrations Due to the Vibratory Roller: A Pilot Study. Sensors 2019, 19, 5420. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, D.-S.; Lee, J.-S. Propagation and attenuation characteristics of various ground vibrations. Soil Dyn. Earthq. Eng. 2000, 19, 115–126. [Google Scholar] [CrossRef]
- Tong, X.; Yang, H.; Wang, L.; Miao, Y. The Development and Field Evaluation of an IoT System of Low-Power Vibration for Bridge Health Monitoring. Sensors 2019, 19, 1222. [Google Scholar] [CrossRef] [Green Version]
- Soman, R.; Kudela, P.; Balasubramaniam, K.; Kumar Singh, S.; Malinowski, P. A Study of Sensor Placement Optimisation Problem for GuidedWave-Based Damage Detection. Sensors 2019, 19, 1856. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akbarzadeh, V.; Lévesque, J.-C.; Gagné, C.; Parizeau, M. Efficient Sensor Placement Optimisation Using Gradient Descent and Probabilistic Coverage. Sensors 2014, 14, 15525–15552. [Google Scholar] [CrossRef] [PubMed]
- Qin, T.; Lin, M.; Cao, M.; Fu, K.; Ding, R. Effects of Sensor Location on Dynamic Load Estimation in Weigh-in-Motion System. Sensors 2018, 18, 3044. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Fu, Y.; Chow, R.; Spencer, B., Jr.; Park, J.; Mechitov, K. Development of a High-Sensitivity Wireless Accelerometer for Structural Health Monitoring. Sensors 2018, 18, 262. [Google Scholar] [CrossRef]
- Adamo, F.; Attivissimo, F.; Lanzolla, A.M.L.; Saponaro, F.; Cervellera, V. Assessment of the uncertainty in human exposure to vibration: An experimental study. IEEE Sens. J. 2014, 14, 474–481. [Google Scholar] [CrossRef]
- British standard. In Noise Control on Construction and Open Sites. Part 4: Code of Practice of Noise and Vibration Control Applicable to Piling Operation; BS 5228-4:1992; British Standards Institution: London, UK, 1992.
- Evaluation and Measurement for Vibration in Buildings—Part 2: Guide to Damage Levels from Ground Borne Vibration; BS 7385-2:1993; British Standards Institution: London, UK, 1993.
- Structural Vibration Part 3: Effects of Vibration on Structures; DIN 4150-3:1999; DIN Germany Institute: Berlin, Germany, 1999.
- Studer, J.; Suesstrunk, A. Swiss Standard for Vibrational Damage to Buildings, Comments on SN 640 312, Effects of Vibrations on Structures. In Proceedings of the 10th International Conference of Soil Mechanics and Foundation Engineering, Stockholm, Sweden, 15–19 June 1981; pp. 307–312. [Google Scholar]
- Eurocode 3—Design of Steel Structures. Part 5: Piling; ENV1993; European Committee of Standardisation: Brussels, Belgium, 1998.
- Assessment of the Harmfulness of Vibrations Transmitted Through the Ground to Buildings; PN-B-02170:2016–12; Cracow University of Technology: Kraków, Poland, 2016. (In Polish)
- Athanasopoulos, G.; Pelekis, P. Ground vibrations from sheetpile driving in urban environment: Measurements, analysis and effects on buildings and occupants. Soil Dyn. Earthq. Eng. 2000, 19, 371–387. [Google Scholar] [CrossRef]
- Ekanayake, S.; Liyanapathirana, D.; Leo, C. Influance zone around a closed-ended pile during vibratory driving. Soil Dyn. Earthq. Eng. 2013, 53, 26–36. [Google Scholar] [CrossRef]
- Czech, K.; Gosk, W. Impact of the operation of a Tri-Band Hydraulic Compactor on the Technical Condition of a Residental Building. Appl. Sci. 2019, 9, 336. [Google Scholar] [CrossRef] [Green Version]
- Wyjadlowski, M. Methodology of dynamic monitoring of structures in the vicinity of hydrotechnical works—selected case studies. Studia Geotech. Mech. 2017, 39, 121–129. [Google Scholar] [CrossRef] [Green Version]
- Brzakala, W.; Herbut, A.; Rybak, J. Recommendations for ground vibrations survey in course of geotechnical works. In Proceedings of the International Multidisciplinary Scientific GeoConference Surveying Geology and Mining Ecology Management SGEM, Albena, Bulgaria, 17–26 June 2014; Volume 2, pp. 747–754. [Google Scholar]
- Bertola, N.; Papadopoulou, M.; Vernay, D.; Smith, I. Optimal Multi-Type Sensor Placement for Structural Identification by Static-Load Testing. Sensors 2017, 17, 2904. [Google Scholar] [CrossRef] [Green Version]
- Abedi, A.S.; Hataf, N.; Ghahramani, A. Analytical solution of the dynamic response of buried pipelines under blast wave. Int. J. Rock Mech. Min. Sci. 2016, 88, 301–306. [Google Scholar] [CrossRef]
- Jiang, N.; Gao, T.; Zhou, C.; Luo, X. Safety assessment of upper buried gas pipeline under blasting vibration of subway tunnel: A case study in Beijing subway line. J. Vibroeng. 2019, 21, 888–900. [Google Scholar] [CrossRef]
- Ainalis, D.; Kaufmann, O.; Tshibangu, J.P.; Verlinden, O.; Kouroussis, G. Modelling the source of blasting for the numerical simulation of blast-induced ground vibrations: A review. Rock Mech. Rock Eng. 2017, 50, 171–193. [Google Scholar] [CrossRef]
- Das, B.; Ramana, G. Principles of Soil Dynamics; Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]
- Kramer, S. Geotechnical Earthquake Engineering; Pearson Education: London, UK, 1996. [Google Scholar]
- Towhata, I. Geotechnical Earthquake Engineering; Springer: Heidelberg, Germany, 2008. [Google Scholar]
- Hwang, J.; Tu, T. Ground vibration due to dynamic compaction. Soil Dyn. Earthq. Eng. 2006, 26, 337–346. [Google Scholar] [CrossRef]
- Mabsout, M.; Tassoulas, S. A Finite Element Model for the Simulation of Pile Driving. Numerical Methods in Engineering. Int. J. Numer. Methods Eng. 1994, 37, 257–278. [Google Scholar] [CrossRef]
- Dym, C.L. Attenuation of Ground Vibration. Sound Vib. 1976, 10, 32–34. [Google Scholar]
- Masoumi, H.; Degrande, G.; Lombaert, G. Prediction of free field vibrations due to pile driving using a dynamic soil-structure interaction formulation. Soil Dyn. Earthq. Eng. 2007, 27, 126–143. [Google Scholar] [CrossRef]
- Giannaros, E.; Kotzakolios, T.; Kostopoulos, V. Blast response of composite pipeline structure using finite element techniques. J. Compos. Mater. 2016, 50, 3459–3476. [Google Scholar] [CrossRef]
- Won, J.H.; Kim, M.K.; Kim, G.; Cho, S.H. Blast-induced dynamic response on the interface of a multilayered pipeline. Struct. Infrastruct. Eng. 2014, 10, 80–92. [Google Scholar] [CrossRef]
- Verruijt, A. An Introduction to Soil Dynamics; Springer: Berlin, Germany, 2010. [Google Scholar]
- Carcione, J. Wave Fields in Real Media: Wave Propagation in Anisotropic, an Elastic and Porous Media; Elsevier Science: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Lysmer, J.; Kuhlemeyer, R.L. Finite dynamic model for infinite media. J. Eng. Mech. Div. 1969, 95, 859–877. [Google Scholar]
- Turan, A.; Hafez, D.; El Naggar, M. The performance of inclined secant micro-pile walls as active vibration barriers. Soil Dyn. Earthq. Eng. 2013, 55, 225–232. [Google Scholar] [CrossRef]
- Goble, G.G.; Hery, P. Influence of residual force on pile drivability analysis. In Proceedings of the 2nd International Conference on the Application of Stress Waves to Piles, Stockholm, Sweden, 27–30 May 1984; pp. 154–161. [Google Scholar]
- Chen, X.; Birk, C.; Song, C. Numerical modelling of wave propagation in anisotropic soil using a displacement unit-impulse-response-based formulation of the scaled boundary finite element method. Soil Dyn. Earthq. Eng. 2014, 65, 243–255. [Google Scholar] [CrossRef]
- Wrana, B. Soil Dynamics. Computation Models; Wydawnictwo Politechniki Krakowskiej: Kraków, Poland, 2016. [Google Scholar]
- Kerner, C.; Dyer, B.; Worthington, M. Wave propagation in a vertical transversely isotropic medium: Field experiment and model study. Geophys. J. Int. 1989, 97, 295–309. [Google Scholar] [CrossRef] [Green Version]
- Woods, R. Screening of Surface Waves in Soils. J. Soil Mech. Found. Div. 1968, 94, 951–980. [Google Scholar]
- Woods, R. Dynamics Effects of Pile Installations on Adjacent Structures. NCHRP253. Synthesis 253; Transportation Research Board: Washington, DC, USA, 1997. [Google Scholar]
- Ulgen, D.; Toygar, O. Screening effectiveness of open and in-filled wave barriers: A full-scale experimental study. Constr. Build. Mater. 2015, 86, 12–20. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. A 2007, 365, 303–315. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Soman, R.; Malinowski, P. Optimization of sensor placement for structural health monitoring: A review. Struct. Health Monit. 2019, 18, 963–988. [Google Scholar] [CrossRef]
- Chisari, C.; Macorini, L.; Amadio, C.; Izzuddin, B.A. Optimal sensor placement for structural parameter identification. Struct. Multidiscip. Optim. 2017, 55, 647–662. [Google Scholar] [CrossRef]
- Blachowski, B.; Tauzowski, P.; Swiercz, A.; Jankowski, Ł. Topology optimization approach for dense Sensor network distribution over large bridge structures. In Proceedings of the IX ECCOMAS Thematic Conference on Smart Structures and Materials SMART, Paris, France, 8–11 July 2019; pp. 284–290. [Google Scholar]
- Stolarik, M.; Pinka, M.; Nedoma, J. Ground-Borne Vibration Due to Construction Works with Respect to Brownfield Areas. Appl. Sci. 2019, 9, 3766. [Google Scholar] [CrossRef] [Green Version]
- Sun, C.; Yu, Y.; Li, V.O.K.; Lam, J.C.K. Multi-type sensor placements in Gaussian spatial fields for environmental monitoring. Sensors 2019, 19, 189. [Google Scholar] [CrossRef] [Green Version]





| Dynamic Shear Modulus Gxz [MPa] | Young’s Modulus in the Plane of Isotropy Ex [MPa], Ey = Ex | Young’s Modulus in the Plane Perpendicular to the Plane of Isotropy Ez [MPa] | ||
|---|---|---|---|---|
| Case 1 | Deposit 1 | Gxz,1 = 30.0 | Ex,1 = 116.0 | Ez,1 = 85.9 |
| Deposit 2 | Gxz,2 = 30.0 | Ex,2 = 116.0 | Ez,2 = 85.9 | |
| Case 2 | Deposit 1 | Gxz,1 = 300.0 | Ex,1 = 1160.0 | Ez,1 = 850.9 |
| Deposit 2 | Gxz,2 = 30.0 | Ex,2 = 116.0 | Ez,2 = 85.9 | |
| Case 3 | Deposit 1 | Gxz,1 = 30.0 | Ex,1 = 116.0 | Ez,1 = 85.9 |
| Deposit 2 | Gxz,2 = 300.0 | Ex,2 = 1160.0 | Ez,2 = 850.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herbut, A.; Rybak, J.; Brząkała, W. On a Sensor Placement Methodology for Monitoring the Vibrations of Horizontally Excited Ground. Sensors 2020, 20, 1938. https://doi.org/10.3390/s20071938
Herbut A, Rybak J, Brząkała W. On a Sensor Placement Methodology for Monitoring the Vibrations of Horizontally Excited Ground. Sensors. 2020; 20(7):1938. https://doi.org/10.3390/s20071938
Chicago/Turabian StyleHerbut, Aneta, Jarosław Rybak, and Włodzimierz Brząkała. 2020. "On a Sensor Placement Methodology for Monitoring the Vibrations of Horizontally Excited Ground" Sensors 20, no. 7: 1938. https://doi.org/10.3390/s20071938
APA StyleHerbut, A., Rybak, J., & Brząkała, W. (2020). On a Sensor Placement Methodology for Monitoring the Vibrations of Horizontally Excited Ground. Sensors, 20(7), 1938. https://doi.org/10.3390/s20071938






