1. Introduction
Micro-electromechanical systems (MEMS) gyroscopes are widely used to measure the rotation rate and have many advantages, such as low cost, small size, low power consumption, good complementary metal-oxide semiconductor (CMOS) compatibility, and suitability for batch fabrication [
1]. Furthermore, the demand for high-performance micro-machined gyroscopes is growing in platform stabilization, industrial measurement, and many other areas [
2,
3]. A typical capacitive MEMS gyroscope interface is composed of a capacitance-to-voltage converter (C/V) and an analog-to-digital converter (ADC) [
1]. For high precision MEMS gyroscopes, an ADC should have features of high signal-to-noise and distortion ratio (SNDR), a low noise floor, and stable performances under different temperatures and process errors.
Among the various techniques for implementing the inertial sensor digital output, sigma-delta (ΣΔ) modulators are widely used, since they combine the benefits of feedback and inherent ADC [
4], which can increase the stability of the system. Additionally, ΣΔ modulators are normally used as high-resolution ADCs with low power. The sampling rate is well above the Nyquist rate to spread the quantization noise over a larger frequency band, and a high amplification in the loop filter causes a suppression of the quantization noise [
5].
Since the output of MEMS gyroscopes is a narrowband amplitude-modulated signal, a bandpass ΣΔ modulator is more appropriate than a low-pass ΣΔ modulator [
6,
7]. The noise is shaped around the notch frequency in the pass-band of the filter. A continuous-time (CT) circuit technique is often applied for the design of the interface application-specific integrated circuit (ASIC) to achieve both a low noise floor and low power consumption [
8]. Compared with discrete-time (DT) techniques, it avoids noise folding problems and lowers the requirements for the first operational amplifier in the ΣΔ modulators. Therefore, the CT bandpass ΣΔ modulator is more suitable for the readout circuits of MEMS gyroscopes. A high-order DT force-feedback bandpass ΣΔ modulator was presented by Dong,Y. et al. [
7]. This architecture uses a relatively low sampling frequency and thus reduces the requirements for the circuit compared to a low-pass ΣΔ modulator. On the basis of this work, Dong,Y. et al. then proposed a sixth-order CT force-feedback bandpass ΣΔ modulator for the sense mode of MEMS gyroscopes [
9].
However, a CT circuit is sensitive to process, temperature, and voltage variations [
10], as filter time constants are a function of resistances or transconductances. Since there is a narrow bandwidth signal in gyroscope readout systems, the relative matching requirements on the electronic filter are stringent [
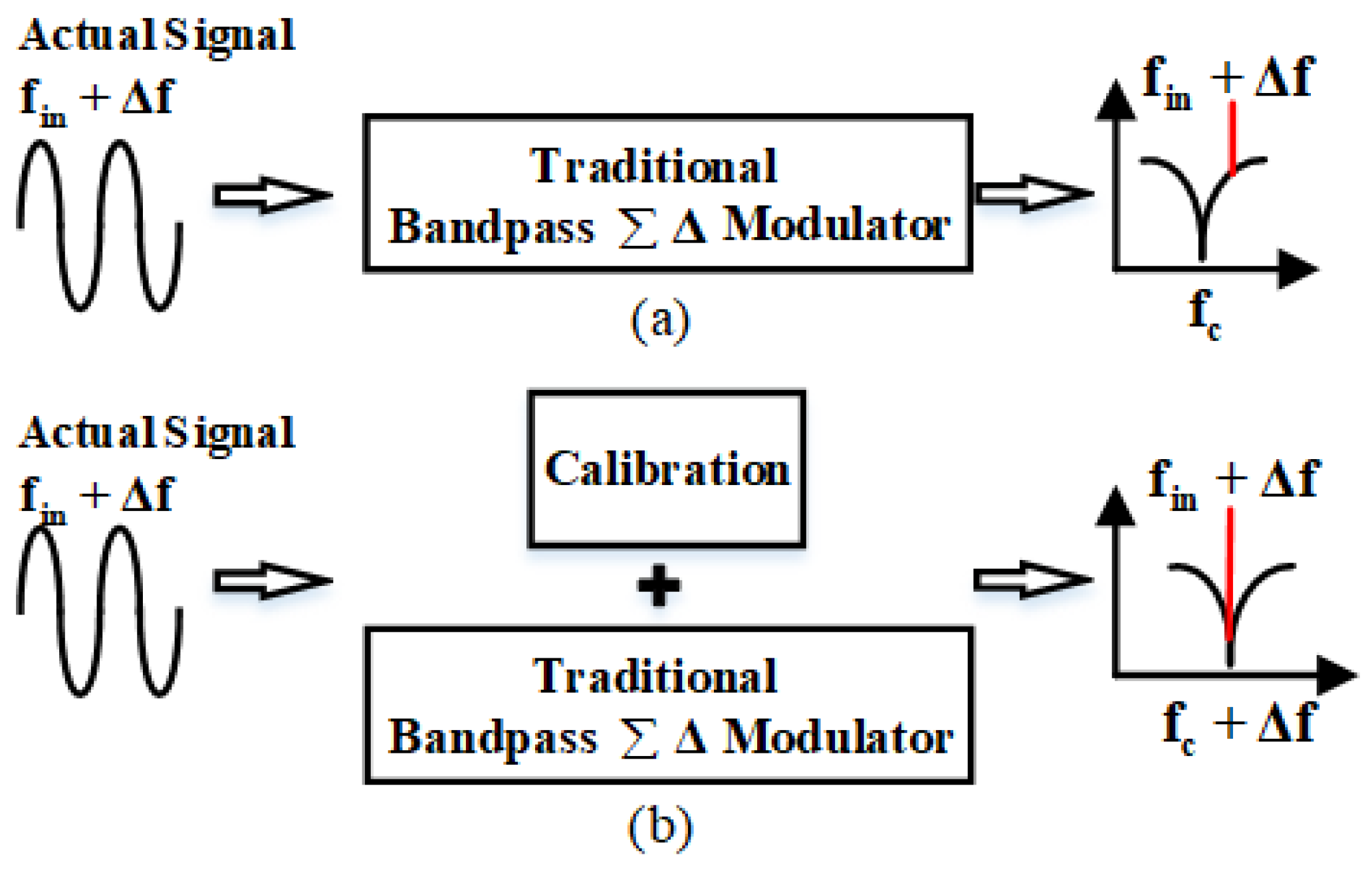
11]. As shown in
Figure 1a, the actual signal is affected by the above factors and there is a frequency deviation from the ideal signal. Therefore, for high-precision MEMS gyroscopes, it is important that the notch frequency of the bandpass ΣΔ ADC track the change of MEMS resonant frequency, which is depicted in
Figure 1b. Furthermore, due to disturbance of the external environment and long-term drifts, it is only the initial calibration of the frequency matching that does not meet the work requirements. Therefore, it is necessary to tune the ΣΔ ADC center frequency in the whole operation process with an online calibration module that is able to work continuously [
11].
To avoid the mismatch problems of
RC times or transconductors, a method of using replica circuits is commonly used. The systems in [
12,
13] use the same capacitor array in the CT integrator and the calibration circuit. In the calibration circuit, a new voltage signal, depending on the capacitor, is compared with the reference voltage. Then a control capacitor code is generated and sent back to the CT integrator. This method limits the continuity of tuning and introduces parasitic capacitance and resistance. The system presented in [
14,
15] uses test signals to achieve mode matching. However, the module of signal tone generation is off-chip with extra area. Another tuning system is described in [
11] based on noise observation, which adds an area to compare the noise power in two bands located symmetrically above and below the node point. However, the signal spectra cannot be of ideal symmetry and the correction method is composed of multiple modules that are complex to design. The tuning schemes are implemented by changing the transconductance in an operational amplifier, which affects the linearity of the system [
13,
16].
In this paper, a novel automatic tuning system based on metal-oxide semiconductor (MOS) resistance is presented to lower noise floors and to improve the adaptability to temperature drifts and process errors. An on-chip signal observation works overhead with a replica of a loop filter in the ΣΔ modulator to solve the filter tuning problem, which can increase frequency range and tuning accuracy. The measurement results indicate that the tuning range of the bandpass ΣΔ modulator is from 6 to 15 kHz at a temperature ranging from −45 to 60 °C, thus allowing it to be applied to the interface circuit of gyroscopes with different resonant frequencies. The specifications and principles of the background frequency tuning are explained in
Section 2; the design of the interface ASIC is shown in
Section 3; and
Section 4 presents the measurement results of the frequency tuning circuit.
2. Basic Principles of Auto-tuning
The block diagram of the automatic tuning based on the
modulator is shown in
Figure 2. The system consists of a conventional CT second-order
modulator with a 3-bit quantizer and a signal observation. The control voltage
which is generated by the signal observation can tune the time constants of the electronic filters to further change the center frequency of the bandpass
modulator.
The following describes the working process of the automatic tuning. The common input signal
flows into the two filters with the same open-loop transfer function H(s). The structure and parameters of the loop filter in the signal observation are the same as those of the automatic tuning filter in the
modulator, which are represented by the filled in slashes in
Figure 2. In the same chip, the two signals
and
are almost affected to the same extent by an ASIC process error and temperature variations. Another input signal,
, with the same frequency as
, is a standard signal that is supplied externally. The signals
and
, with the same frequency, flow into the phase frequency detector (PFD). The PFD can generate different voltage values according to the signal frequency and the phase difference between the two signals. The output voltage of the PFD passes through an integrator to eliminate voltage ripple. Finally, the integrator generates the control voltage signal
, which is applied to the tunable voltage-mode MOS resistances in the loop filters. The control voltage
is applied to the two loop filters simultaneously to keep the same H(s).
According to the principle of automatic tuning, the interface ASIC with a signal observation can track and adjust the notch center frequency for gyroscopes of different resonant frequencies, and can have a good process and environmental adaptability. The following content in this section introduces the module design related to auto-tuning.
2.1. CT Bandpass ΣΔ Modulator Archiecture
The bandpass
modulator employs a single-loop second-order
modulator with a 3-bit quantizer using feedforward and feedback paths, as shown in
Figure 3. This work uses a second-order
architecture because it is stable and easy to design for the observation. Meanwhile, a 3-bit quantizer is used for its advantages of enhancing dynamic range and decreasing quantization noise. The signal transfer function (STF) and the noise transfer function (NTF) of the system in
Figure 3 are as follows:
2.2. Loop Filter Architecture in Signal Obsesrvation
The core of the signal observation is the design of the loop filter. As is described above, the architectures of the two loop filters in the
modulator and the signal observation are identical. In
Figure 3 and
Figure 4, the same modules and parameters are filled with slashes. If the signal observation and the
modulator have different loop filter architectures, the operational amplifier and passive devices will be different and will introduce different nonlinear errors. In addition, different layouts will bring in different parasitic capacitors and resistors. These problems are difficult to correct in different forms of structure. Therefore, the signal observation adopts the same loop filter structure as the
modulator, which can reduce the mismatch error caused by non-ideal factors and can further improve SNDR.
The transfer function of the observation system is expressed as
In this circuit design, all of the electronic filters adopt the same parameters; thus, . When the frequency of the input signal changes, the frequency response of NTF in (2) and TF in (3) will change correspondingly, as shown in expressions (4) and (5).
Figure 5 depicts the frequency response of the transfer functions (4) and (5). Obviously, the corresponding frequency of the peak response in the signal observation is consistent with the notch frequency in the
modulator, which is the main principle of the signal observation design.
2.3. Control Voltage Generation
Figure 6 shows the block diagram of the signal observation.
passes through the loop filter before flowing into Comparator 1.
directly flows into Comparator 2 to generate a square wave
. The square wave
with different phases is derived from Comparator 1, which compares signal
with a DC standard voltage. Next, an Exclusive OR (XOR) gate calculates the phase difference between
and
to obtain the digital signal
and the charge pump converts it into an analog signal
. The relation between the value of
and the phase difference
is:
where
is the coefficient associated with the charge pump.
Finally, the control voltage
is obtained by the integral operation (7).
Figure 7 shows the above operation waveforms transformation. The voltage
directly determines the values of the MOS resistances, which means that
determines the time constants of the electronic filters. Furthermore,
can automatically adjust the notch frequency in the
modulator.
4. Measurement Results
A chip micrograph of the ASIC is shown in
Figure 12, which was fabricated in SMIC 0.18-μm Mixed Signal 1P6M COMS process. A 5V power supply voltage helps the gyroscope achieve high precision. In the layout design, the electrical filters in the signal observation and the
modulator are located as close to each other as possible. The ASIC occupies 2.4 mm
2 of the active area and consumes 7.8 mA. The area required for the signal observation is approximately 0.99 mm
2. The performance of the modulator was evaluated using a high-resolution sinusoidal source as input signals and a digital square wave source as sampling signal.
The circuit was first tested at 25 °C with a sampling clock
= 1.5 MHz. Since only narrowband signal is concerned, SNDR is calculated as the output signal power to noise and distortion power in a two-sided bandwidth of 200 Hz. A total of five chips were tested to verify the repeatability of the data. The measured SNDR is presented versus a 15 kHz input signal amplitude in
Figure 13. The input-referred dynamic range (DR) is approximately 106 dBV [
22], and the maximum SNDR is 86.4 dB when a −14 dBV input signal is applied. MEMS gyroscope interface circuits measure tiny capacitors variations. Since the amplitude of the input signal is small, the performance of SNDR is not better than commercial ADC. However, for gyroscopes, in-band noise (IBN) is more relevant than the overall SNDR. It needs to be noted that the amplitudes of input signals are −26 dBV in the following measured performances.
The effect of auto-tuning is illustrated in
Figure 14a,b, which shows two output spectrums corresponding to the 9 kHz and 15 kHz input sinewaves.
Figure 14c,d shows the partial view of the output spectrum near the resonant frequency, which indicates the noise floor below −120 dB in a 400 Hz bandwidth. In the same situation, the signal observation is turned off and the control voltage is fixed externally to tune the noise shaping notch at 11 kHz. There is a mismatch between the center frequency of the notch and the input signal frequency, as is depicted in
Figure 15. This is better illustrated in
Figure 16, IBN, SNDR, and frequency deviation (
) are shown versus different input signal frequencies with signal observation on and off. IBN calculates the power spectral density within the 200 Hz bandwidth. With signal observation disabled, the performances are significantly better at an input signal of 11 kHz than other input signal frequencies. The maximum IBN deviation is 10.96 dB and the maximum SNDR deviation is 10.28 dB. For frequency deviation, the further the input signal strays from 11 kHz, the larger the deviation. The maximum frequency deviation can be up to 5140 Hz. With signal observation enabled, it can be noted that the IBN is below −96 dB and the SNDR is above 74 dB, with the frequency ranging from 6 to 15 kHz. Due to low-frequency noise, the noise-shaping is slightly degraded when the input signal is below 9 kHz and frequency deviation significantly decreases, with a maximum value of less than 110 Hz.
Figure 16a,b and c show that the smaller the frequency deviation, the larger the value of the SNDR and the lower the value of the IBN. A total of five chips were tested to verify the repeatability of the data. This work defines a new parameter SNDR coefficient with frequency (S.CF) to depict the relative change of the SNDR, which is calculated in (10). The S.CF is reduced to 1.13%/kHz with signal observation.
To verify that temperature variations can be compensated by filter tuning, the ASIC temperature was varied between −45 and 60 °C.
Table 2 shows the IBN and the SNDR corresponding to the three different cases of temperature (−45, 25, and 60 °C) with both disabled and enabled signal observation when a 11 kHz input signal is applied. The three temperature cases represent the minimum, normal and maximum temperatures for a chip to work properly. With signal observation disabled, the center frequency of the notch shifted with temperature. The frequency deviation is up to 2230 Hz at −45 °C and 1555 Hz at 60 °C. With signal observation enabled, the notch frequency is basically coincidental with the input signal frequency and the frequency difference is below 0.5% under the above test conditions. The measured IBN is about −100 dB and the SNDR is above 78 dB for each case. From these data, it can be seen that the circuit is stable in the temperature range of −45 to 60 °C. Similar to the definition of S.CF, a parameter SNDR coefficient with temperature (S.CT) is used to describe the relative change of the SNDR with temperature, as calculated in (11). The S.CT has been reduced from 0.091 to 0.023%/°C.
Table 3 shows a summary of the performances of the modulator in this work and a comparison with previously reported auto-tuning circuits for CT
modulators. For fair comparison, only
modulators which were tested or simulated without sensors are shown in
Table 3, and [
14] is designed for MEMS gyroscope interface circuits. Compared with other works, this work thoroughly tested the auto-tuning
modulator at different frequency input signals from 6 to 15 kHz and at different temperatures from −45 to 60 °C. It can reduce the relative variation of the SNDR under different working conditions and can increase the tuning accuracy and tuning range. The value of IBN can be controlled within −96.99 to −103.82 dB, lower than other
modulators working in readout systems. Most of the
modulators for MEMS gyroscopes do not contain frequency tuning or make frequency adjustment off-chip or off-line. A few of these contain auto-tuning circuits, but do not analyze
modulator performance separately [
11,
12].
5. Conclusions
This paper demonstrates the significance of incorporating an active tuning module for modulators in MEMS gyroscopes. A second-order bandpass modulator with a tuning circuit was presented, which can track and adjust the notch center frequency for different resonant frequencies. The implementation of the filter tuning uses a signal observation that contains a filter with the same architecture as the loop filter in the traditional modulator, thus both of them have the same response to the input signal change, temperature variation, and process error. In the signal observation, the phase difference of the standard signal and the output signal through the electrical filter is converted into a control voltage applied to the MOS resistances. With the signal observation, the presented ASIC offers a very high flexibility, thus can be used with different gyroscopes. With input signal frequency ranging from 6 to 15 kHz, the signal observation allows the modulator to perform stably at temperatures between −45 and 60 °C. The filter tuning circuit presented is completely implemented on chip and requires an additional area of 0.99 mm2. With an appropriate architecture design, the resulted bandpass modulator achieves a DR of 106 dB, a maximum SNDR of 86.4 dB, a tuning accuracy below 0.62% (at 11 kHz input signal), a S.CF of 1.13 %/kHz, and a S.CT of 0.023%/°C.