Detection of Multiple Cracks in Four-Point Bending Tests Using the Coda Wave Interferometry Method
Abstract
:1. Introduction
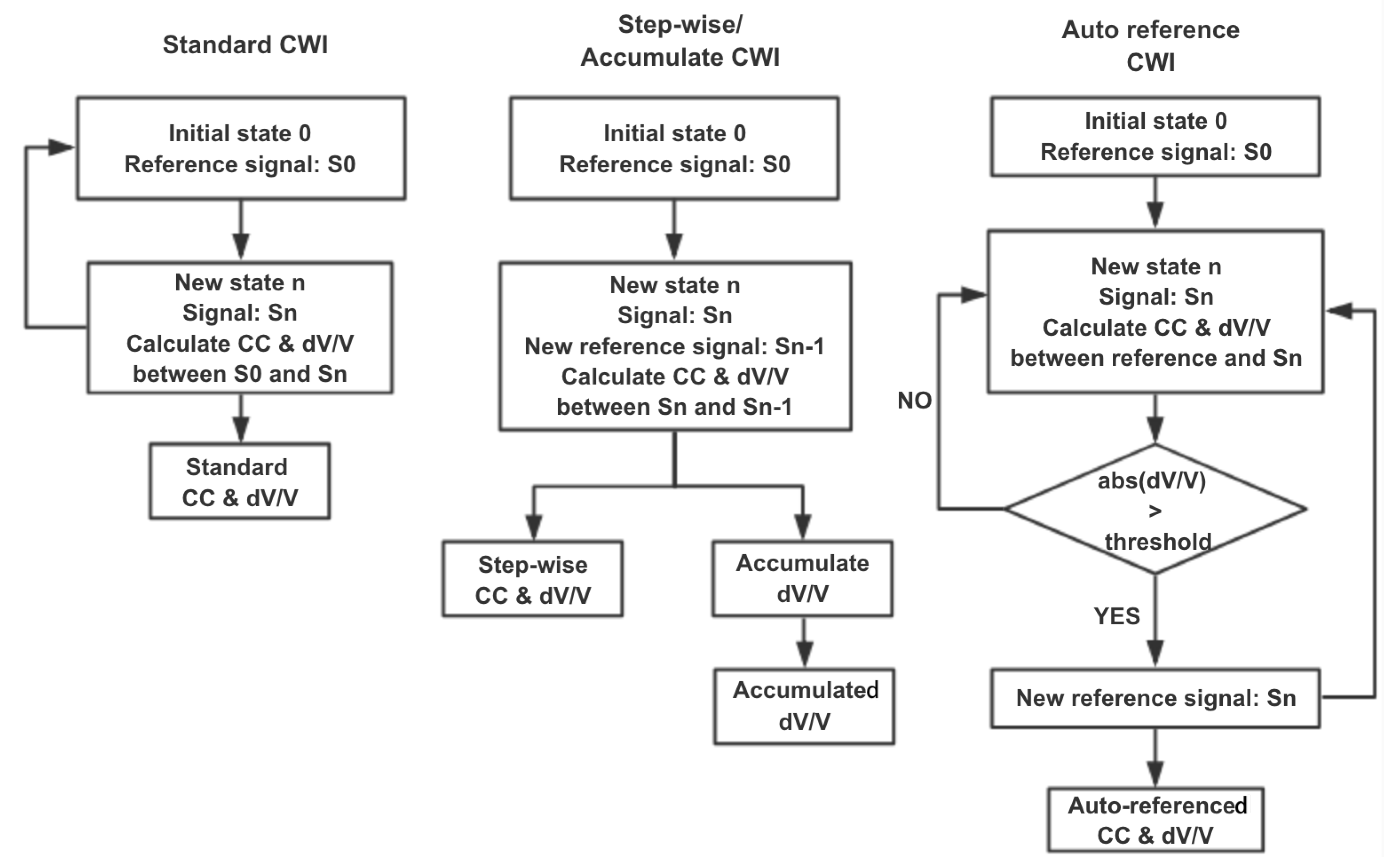
2. Coda Wave Interferometry (CWI) Technique
3. Experimental Investigation
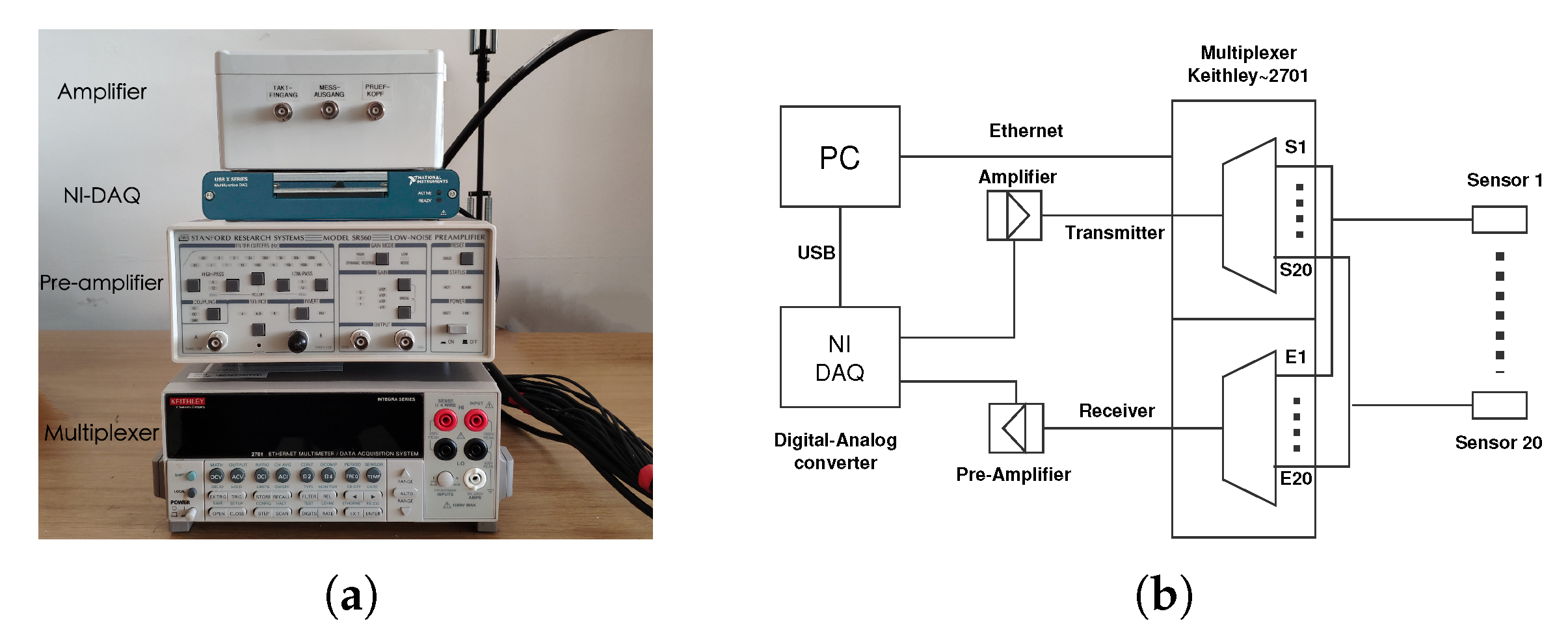
3.1. Transducer and Data Acquisition System
- Amplifier to amplify the input signal of transmitter
- Pre-amplifier with analog filter to improve the signal recorded by receiver
- Digital-analog data acquisition module to convert signal
- Multiplexer with 20 channels to switch between different combinations of transducers
- PC with control software and data storage
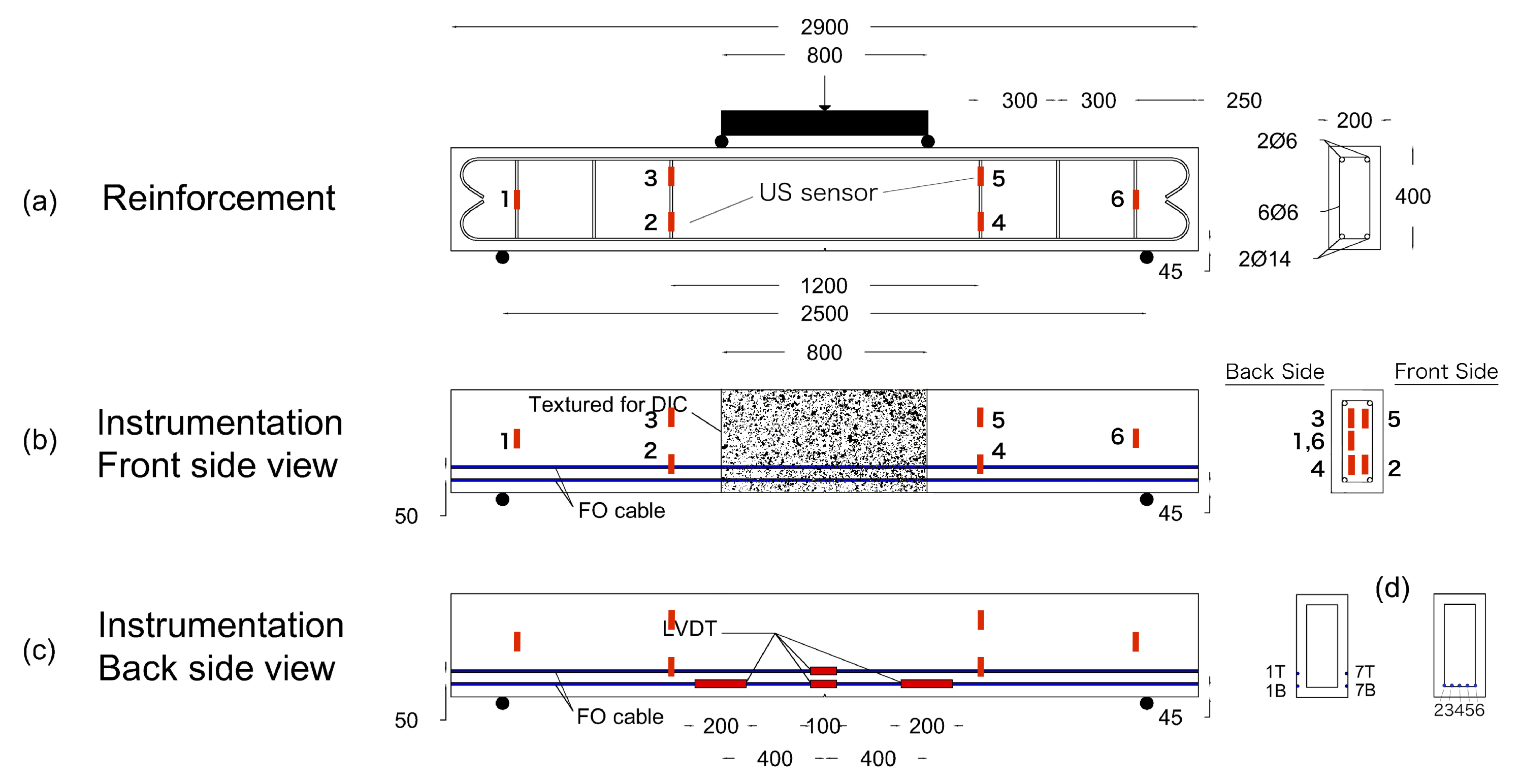
3.2. Experimental Setup
3.2.1. Test Specimen Design
3.2.2. Loading Procedure
4. Results
4.1. Crack Position
4.2. Deflection
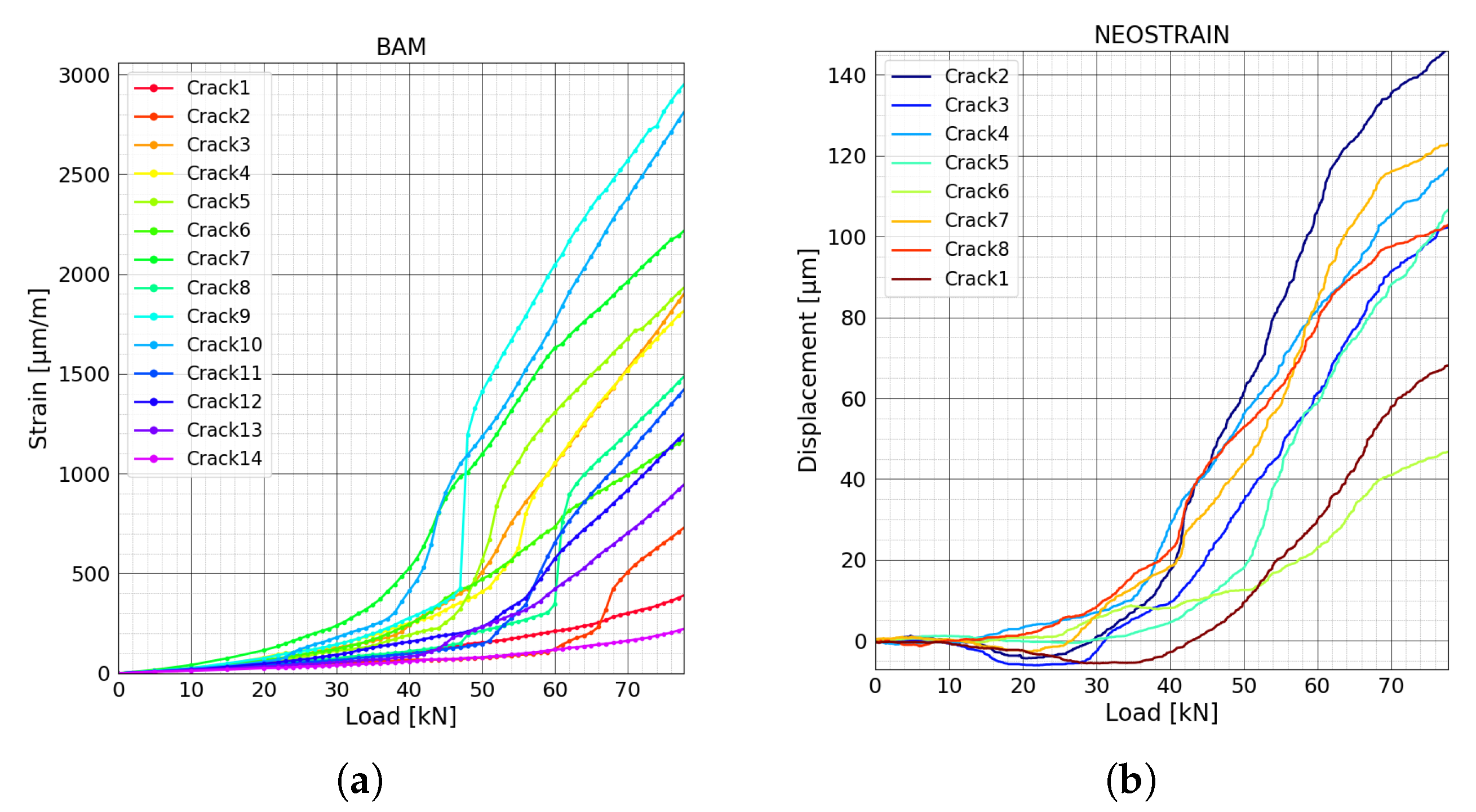
4.3. Displacement and Strain
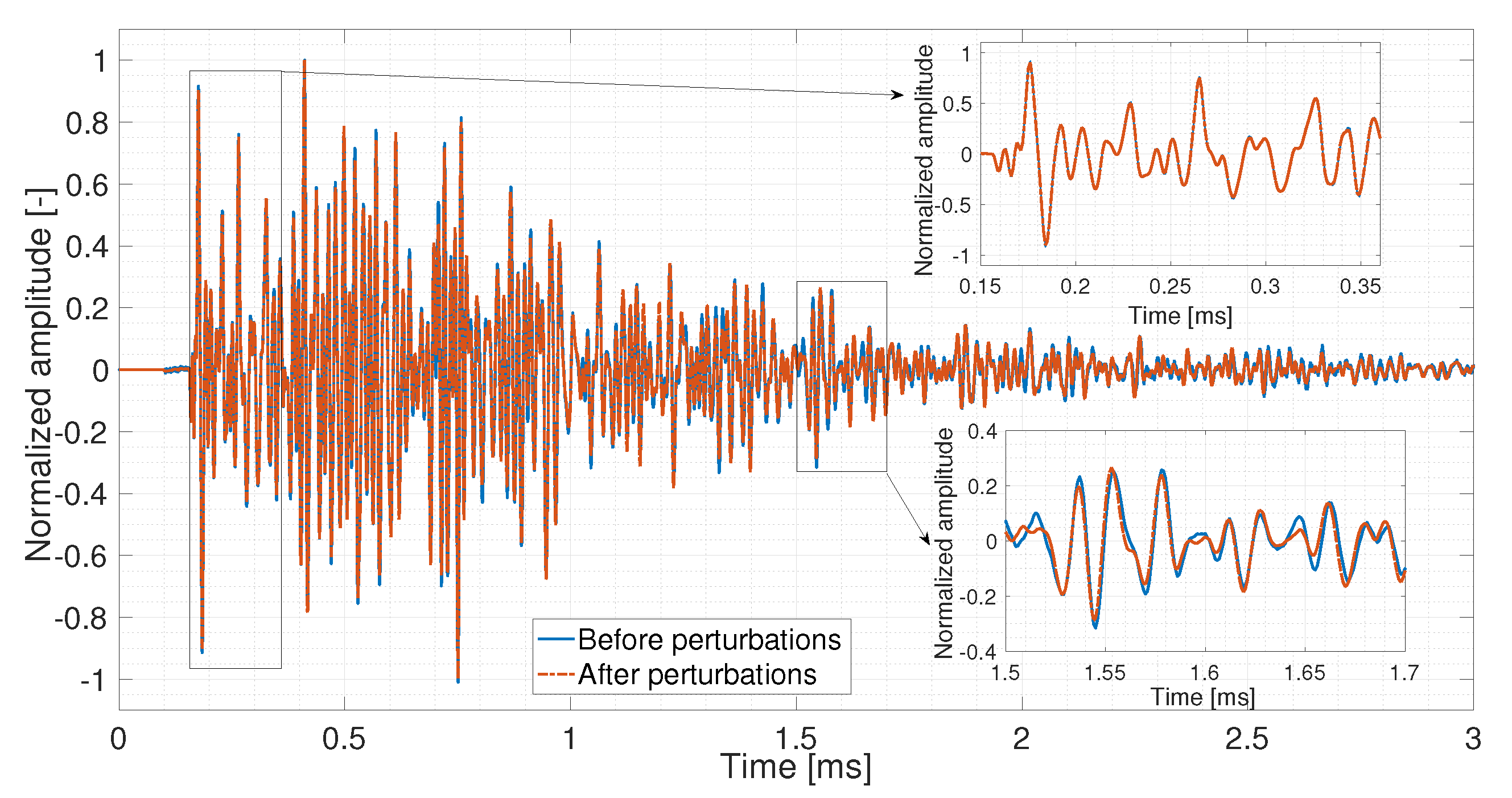
4.4. CWI Technique
4.4.1. Test at BAM
4.4.2. Test at NEOSTRAIN
5. Discussion
5.1. Test at BAM
5.2. Test at NEOSTRAIN
6. Conclusions and Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BAM | Bundesanstalt für Materialforschung und-prüfung |
| RC | reinforced concrete |
| SHM | Structural Health Monitoring |
| NDT | Non-Destructive Testing |
| CWI | Coda Wave Interferometry |
| FOS | Fiber Optics Sensor |
| AE | Acoustic Emission |
| UPV | Ultra Pulse Velocity |
| CC | Correlation Coefficient |
| US | Ultrasonic |
| DIC | Digital Image Correlation |
| LVDT | Linear Variable Differential Transformer |
| COD | Crack Opening Displacement |
References
- Darwin, D.; Dolan, C.W.; Nilson, A.H. Design of concrete structures; McGraw-Hill Education: New York, NY, USA, 2016. [Google Scholar]
- Saarenketo, T.; Scullion, T. Road evaluation with ground penetrating radar. J. Appl. Geophys. 2000, 43, 119–138. [Google Scholar] [CrossRef]
- Lai, W.; Kind, T.; Wiggenhauser, H. Detection of accelerated reinforcement corrosion in concrete by ground penetrating radar. In Proceedings of the XIII Internarional Conference on Ground Penetrating Radar, Lecce, Italy, 21–25 June 2010; pp. 1–5. [Google Scholar]
- Hong, S.X.; Lai, W.; Helmerich, R. Monitoring accelerated corrosion in chloride contaminated concrete with ground penetrating radar. In Proceedings of the 14th International Conference on Ground Penetrating Radar (GPR), Shanghai, China, 4–8 June 2012; pp. 561–566. [Google Scholar]
- Akamatsu, R.; Sugimoto, T.; Utagawa, N.; Katakura, K. Proposal of non contact inspection method for concrete structures using high-power directional sound source and scanning laser doppler vibrometer. Jpn. J. Appl. Phys. 2013, 52, 07HC12. [Google Scholar] [CrossRef]
- Giri, P.; Kharkovsky, S. Detection of surface crack in concrete using measurement technique with laser displacement sensor. IEEE Trans. Instrum. Meas. 2016, 65, 1951–1953. [Google Scholar] [CrossRef]
- Destrebecq, J.F.; Toussaint, E.; Ferrier, E. Analysis of cracks and deformations in a full scale reinforced concrete beam using a digital image correlation technique. Exp. Mech. 2011, 51, 879–890. [Google Scholar] [CrossRef]
- Gencturk, B.; Hossain, K.; Kapadia, A.; Labib, E.; Mo, Y.L. Use of digital image correlation technique in full-scale testing of prestressed concrete structures. Measurement 2014, 47, 505–515. [Google Scholar] [CrossRef]
- Chakraborty, J.; Katunin, A.; Klikowicz, P.; Salamak, M. Early crack detection of reinforced concrete structure using embedded sensors. Sensors 2019, 19, 3879. [Google Scholar] [CrossRef] [Green Version]
- Henault, J.M.; Quiertant, M.; Delepine-Lesoille, S.; Salin, J.; Moreau, G.; Taillade, F.; Benzarti, K. Quantitative strain measurement and crack detection in RC structures using a truly distributed fiber optic sensing system. Constr. Build Mater. 2012, 37, 916–923. [Google Scholar] [CrossRef]
- Villalba, S.; Casas, J.R. Application of optical fiber distributed sensing to health monitoring of concrete structures. Mech. Syst. Signal Process 2013, 39, 441–451. [Google Scholar] [CrossRef]
- Nair, A.; Cai, C. Acoustic emission monitoring of bridges: Review and case studies. Eng. Struct. 2010, 32, 1704–1714. [Google Scholar] [CrossRef]
- Han, Q.; Xu, J.; Carpinteri, A.; Lacidogna, G. Localization of acoustic emission sources in structural health monitoring of masonry bridge. Struct. Control Health Monit. 2015, 22, 314–329. [Google Scholar] [CrossRef]
- Gómez Muñoz, C.; García Márquez, F. A new fault location approach for acoustic emission techniques in wind turbines. Energies 2016, 9, 40. [Google Scholar] [CrossRef] [Green Version]
- Bogas, J.A.; Gomes, M.G.; Gomes, A. Compressive strength evaluation of structural lightweight concrete by non-destructive ultrasonic pulse velocity method. Ultrasonics 2013, 53, 962–972. [Google Scholar] [CrossRef] [PubMed]
- Snieder, R.; Grêt, A.; Douma, H.; Scales, J. Coda wave interferometry for estimating nonlinear behavior in seismic velocity. Science 2002, 295, 2253–2255. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grêt, A.; Snieder, R.; Scales, J. Time-lapse monitoring of rock properties with coda wave interferometry. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Niederleithinger, E.; Wunderlich, C. Influence of small temperature variations on the ultrasonic velocity in concrete. AIP Conf. Proc. 2013, 1511, 390–397. [Google Scholar] [CrossRef]
- Zhang, Y.; Abraham, O.; Tournat, V.; Le Duff, A.; Lascoup, B.; Loukili, A.; Grondin, F.; Durand, O. Validation of a thermal bias control technique for Coda Wave Interferometry (CWI). Ultrasonics 2013, 53, 658–664. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Abraham, O.; Grondin, F.; Loukili, A.; Tournat, V.; Le Duff, A.; Lascoup, B.; Durand, O. Study of stress-induced velocity variation in concrete under direct tensile force and monitoring of the damage level by using thermally-compensated coda wave interferometry. Ultrasonics 2012, 52, 1038–1045. [Google Scholar] [CrossRef] [Green Version]
- Niederleithinger, E.; Sens-Schönfelder, C.; Grothe, S.; Wiggenhauser, H. Coda Wave Interferometry Used to Localize Compressional Load Effects in a Concrete Specimen. In EWSHM—7th European Workshop on Structural Health Monitoring; IFFSTTAR, Inria, Université de Nantes: Nante, France, 2014. [Google Scholar]
- Hilloulin, B.; Zhang, Y.; Abraham, O.; Loukili, A.; Grondin, F.; Durand, O.; Tournat, V. Small crack detection in cementitious materials using nonlinear coda wave modulation. NDT E Int. 2014, 68, 98–104. [Google Scholar]
- Zhang, Y.; Tournat, V.; Abraham, O.; Durand, O.; Letourneur, S.; Le Duff, A.; Lascoup, B. Nonlinear coda wave interferometry for the global evaluation of damage levels in complex solids. Ultrasonics 2017, 73, 245–252. [Google Scholar] [CrossRef]
- Wang, X.; Niederleithinger, E. Coda Wave Interferometry used to detect loads and cracks in a concrete structure under field conditions. In Proceedings of the 9th European Workshop on Structural Health Monitoring Series, Manchester, UK, 10–13 July 2018; pp. 10–13. [Google Scholar]
- Wang, X.; Niederleithinger, E.; Lange, M.; Stolpe, H. Implementation of Ultrasonic Coda Wave Interferometry on a Real Bridge. In Proceedings of the 12th International Workshop on Structural Health Monitoring Series, Stanford, CA, USA, 10–12 September 2019. [Google Scholar]
- Wang, X.; Chakraborty, J.; Klikowicz, P.; Niederleithinger, E. Monitoring a concrete bridge girder with the coda wave interferometry method. In Proceedings of the 5th International Conference on Smart Monitoring, Assessment and Rehabilitation of Civil Structures, Potsdam, Germany, 27–29 August 2019. [Google Scholar]
- Stähler, S.C.; Sens-Schönfelder, C.; Niederleithinger, E. Monitoring stress changes in a concrete bridge with coda wave interferometry. J. Acoust. Soc. Am. 2011, 129, 1945–1952. [Google Scholar] [CrossRef] [Green Version]
- Niederleithinger, E.; Wolf, J.; Mielentz, F.; Wiggenhauser, H.; Pirskawetz, S. Embedded ultrasonic transducers for active and passive concrete monitoring. Sensors 2015, 15, 9756–9772. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bassil, A.; Wang, X.; Chapeleau, X.; Niederleithinger, E.; Abraham, O.; Leduc, D. Distributed fiber optics sensing and coda wave interferometry techniques for damage monitoring in concrete structures. Sensors 2019, 19, 356. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Planès, T.; Larose, E. A review of ultrasonic Coda Wave Interferometry in concrete. Cem. Concr. Res. 2013, 53, 248–255. [Google Scholar] [CrossRef]
- Sens-Schönfelder, C.; Wegler, U. Passive image interferometry and seasonal variations of seismic velocities at Merapi Volcano, Indonesia. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Niederleithinger, E.; Wang, X.; Herbrand, M.; Müller, M. Processing ultrasonic data by coda wave interferometry to monitor load tests of concrete beams. Sensors 2018, 18, 1971. [Google Scholar] [CrossRef] [Green Version]
- Schlune, H.; Student, P.; Plos, M.; Gylltoft, K.; Se, K. Non-linear Finite Element Analysis for Practical Application; NORSK BETONGFORENING: Solli, Norway, 2019; p. 82. [Google Scholar]
- Bassil, A.; Niederleithinger, E.; Wang, X.; Chapeleau, X.; Leduc, D.; Abraham, O.; Kadoke, D.; Breithaupt, M.; Potschke, S. Distributed Fiber Optic Sensors for Multiple Crack Monitoring in Reinforced Concrete Structures. In Proceedings of the 12th International Workshop on Structural Health Monitoring Series, Stanford, CA, USA, 10–12 September 2019. [Google Scholar]















| Technique | BAM | NEOSTRAIN |
|---|---|---|
| US transducer | 6 SO807 | 4 SO807 |
| Strain gauge | 0 | 2 vibrating wire strain gauges |
| 2 rebar stress meters | ||
| LVDT | 4 | 1 |
| Fiber optic sensor | 9 fibers | 0 |
| DIC | 80 cm × 40 cm | 290 cm × 40 cm |
| Phase | Crack 1 | Crack 2 | Crack 3 | Crack 4 | Crack 5 | Crack 6 | Crack 7 |
|---|---|---|---|---|---|---|---|
| Crack formation | 67 kN | 60 kN | 40 kN | 45 kN | 45 kN | 40 kN | 38 kN |
| Stabilised cracking | None | 68 kN | 56 kN | 56 kN | 56 kN | 61 kN | 61 kN |
| Phase | Crack 8 | Crack 9 | Crack 10 | Crack 11 | Crack 12 | Crack 13 | Crack 14 |
| Crack formation | 48 kN | 47 kN | 38 kN | 51 kN | 51 kN | 42 kN | 70 kN |
| Stabilised cracking | 60 kN | 50 kN | 46 kN | 60 kN | 60 kN | 58 kN | None |
| Phase | Crack 1 | Crack 2 | Crack 3 | Crack 4 | Crack 5 | Crack 6 | Crack 7 | Crack 8 |
|---|---|---|---|---|---|---|---|---|
| Crack formation | 41 kN | 40 kN | 41 kN | 37 kN | 41 kN | 53 kN | 41 kN | 41 kN |
| Stabilised cracking | 70 kN | 61 kN | 68 kN | 42 kN | 58 kN | 68 kN | 68 kN | 68 kN |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Chakraborty, J.; Bassil, A.; Niederleithinger, E. Detection of Multiple Cracks in Four-Point Bending Tests Using the Coda Wave Interferometry Method. Sensors 2020, 20, 1986. https://doi.org/10.3390/s20071986
Wang X, Chakraborty J, Bassil A, Niederleithinger E. Detection of Multiple Cracks in Four-Point Bending Tests Using the Coda Wave Interferometry Method. Sensors. 2020; 20(7):1986. https://doi.org/10.3390/s20071986
Chicago/Turabian StyleWang, Xin, Joyraj Chakraborty, Antoine Bassil, and Ernst Niederleithinger. 2020. "Detection of Multiple Cracks in Four-Point Bending Tests Using the Coda Wave Interferometry Method" Sensors 20, no. 7: 1986. https://doi.org/10.3390/s20071986
APA StyleWang, X., Chakraborty, J., Bassil, A., & Niederleithinger, E. (2020). Detection of Multiple Cracks in Four-Point Bending Tests Using the Coda Wave Interferometry Method. Sensors, 20(7), 1986. https://doi.org/10.3390/s20071986






