Spectral Filter Selection for Increasing Chromatic Diversity in CVD Subjects
Abstract
:1. Introduction
2. Methods
2.1. Reflectances
2.1.1. Data Set 1 (D1: Atlas)
2.1.2. Data Set 2 (D2: Scenes)
2.1.3. Data Set 3 (D3: Ishihara and FM100)
2.2. Filters
2.2.1. Band-Pass Filters
2.2.2. Notch Filters
2.2.3. Double Filters
2.2.4. Commercial Filters
2.3. Simulation
2.3.1. CVD Simulation Model
2.3.2. Calculation of the Number of Discernible Colors (NODC)
3. Results
3.1. Selection of Filters
3.2. Effects Produced by the Selected Filters
3.2.1. Changes in Color Coordinates
3.2.2. sRGB Renderings
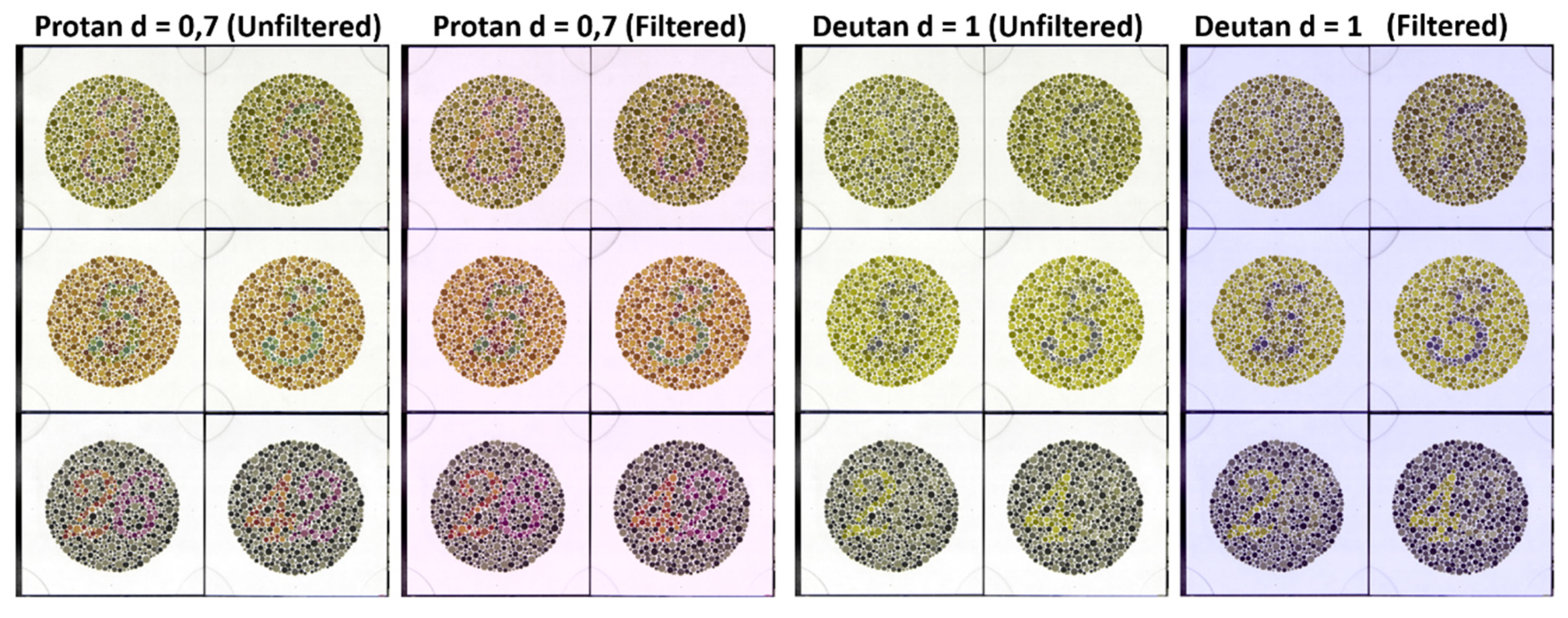
3.2.3. FM100 Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Birch, J. Worldwide prevalence of red-green color deficiency. JOSA A 2012, 29, 313–320. [Google Scholar] [CrossRef] [PubMed]
- Simunovic, M.P. Colour vision deficiency. Eye 2010, 24, 747. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Went, L.N.; Pronk, N. The genetics of tritan disturbances. Hum. Genet. 1985, 69, 255–262. [Google Scholar] [CrossRef] [PubMed]
- Cole, B.L. The handicap of abnormal colour vision. Clin. Exp. Optom. 2004, 87, 258–275. [Google Scholar] [CrossRef]
- Neitz, M.; Neitz, J. Curing color blindness—mice and nonhuman primates. Cold Spring Harb. Perspect. Med. 2014, 4, a017418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Popleteev, A.; Louveton, N.; McCall, R. Colorizer: Smart glasses aid for the colorblind. WearSys 2015, 15, 7–8. [Google Scholar] [CrossRef]
- Simon-Liedtke, J.T.; Farup, I. Multiscale Daltonization in the Gradient Domain. In Proceedings of the Color and Imaging Conference, Vancouver, BC, Canada, 12–16 November 2018. [Google Scholar]
- EnChroma, EnChroma Inc. 2020. Available online: https://enchroma.com/ (accessed on 2 March 2020).
- VINO. Available online: https://www.vino.vi/collections/color-blind-glasses (accessed on 2 March 2020).
- Martínez-Domingo, M.A.; Gómez-Robledo, L.; Valero, E.M.; Huertas, R.; Hernández-Andrés, J.; Ezpeleta, S.; Hita, E. Assessment of VINO filters for correcting red-green Color Vision Deficiency. Opt. Express 2019, 27, 17954–17967. [Google Scholar] [CrossRef]
- Gómez-Robledo, L.; Valero, E.M.; Huertas, R.; Martínez-Domingo, M.A.; Hernández-Andrés, J. Do EnChroma glasses improve color vision for colorblind subjects? Opt. Express 2018, 26, 28693–28703. [Google Scholar] [CrossRef]
- Almutairi, N.; Kundart, J.; Muthuramalingam, N.; Hayes, J.; Citek, K.; Aljohani, S. Assessment of Enchroma Filter for Correcting Color Vision Deficiency. Available online: https://commons.pacificu.edu/work/501bb1bb-1502-475e-aa5e-d8f2d7abde1f (accessed on 3 April 2020).
- Mastey, R.; Patterson, E.J.; Summerfelt, P.; Luther, J.; Neitz, J.; Neitz, M.; Carroll, J. Effect of “color-correcting glasses” on chromatic discrimination in subjects with congenital color vision deficiency. Investig. Ophthalmol. Vis. Sci. 2016, 57, 192. [Google Scholar]
- Patterson, E.J. Glasses for the colorblind: Their effect on chromatic discrimination in subjects with congenital red-green color vision deficiency. In Proceedings of the International Conference on Computer Vision Systems (ICVS), Shenzhen, China, 10–13 July 2017. [Google Scholar]
- Lucassen, M.; Alferdinck, J. Dynamic simulation of color blindness for studying color vision requirements in practice. In Proceedings of the Conference on Colour in Graphics, Imaging, and Vision, Leeds, UK, 19–22 June 2006. [Google Scholar]
- Machado, G.M.; Oliveira, M.M.; Fernandes, L.A.F. A physiologically-based model for simulation of color vision deficiency. IEEE Trans. Vis. Comput. Graph. 2009, 15, 1291–1298. [Google Scholar] [CrossRef]
- Wachtler, T.; Dohrmann, U.; Hertel, R. Modeling color percepts of dichromats. Vis. Res. 2004, 44, 2843–2855. [Google Scholar] [CrossRef] [Green Version]
- Linhares, J.M.M.; Pinto, P.D.; Nascimento, S.M.C. The number of discernible colors perceived by dichromats in natural scenes and the effects of colored lenses. Vis. Neurosci. 2008, 25, 493–499. [Google Scholar] [CrossRef] [PubMed]
- Brettel, H.; Viénot, F.; Mollon, J.D. Computerized simulation of color appearance for dichromats. JOSA A 1997, 14, 2647–2655. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moreland, J.D.; Westland, S.; Cheung, V.; Dain, S.J. Quantitative assessment of commercial filter ‘aids’ for red-green colour defectives. Ophthalmic Physiol. Opt. 2010, 30, 685–692. [Google Scholar] [CrossRef] [PubMed]
- DeMarco, P.; Pokorny, J.; Smith, V.C. Full-spectrum cone sensitivity functions for X-chromosome-linked anomalous trichromats. JOSA A 1992, 9, 1465–1476. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marín-Franch, I.; Foster, D.H. Number of perceptually distinct surface colors in natural scenes. J. Vis. 2010, 10, 9. [Google Scholar] [CrossRef] [Green Version]
- Pastilha, R.C.; Linhares, J.M.M.; Gomes, A.E.; Santos, J.L.A.; Almeida, V.M.N.; Nascimento, S.M.C. The colors of natural scenes benefit dichromats. Vis. Res. 2019, 158, 40–48. [Google Scholar] [CrossRef]
- Masuda, O.; Nascimento, S.M.C. Lighting spectrum to maximize colorfulness. Opt. Lett. 2012, 37, 407–409. [Google Scholar] [CrossRef]
- Schrödinger, E. Theorie der Pigmente von grösster Leuchtkraft. Ann. Phys. 1920, 367, 603–622. [Google Scholar] [CrossRef]
- Thornton, W.A. Color-discrimination index. JOSA 1972, 62, 191–194. [Google Scholar] [CrossRef]
- Ishihara, S. Test for Colour-Blindness; Taylor & Francis: Tokyo, Japan, 1987. [Google Scholar]
- Rite, X. FM 100 Hue Color Vision Test. 100 Hue Test Scoring Tool, Version 3.0. Munsell. 2006. Available online: https://www.color-blindness.com/farnsworth-munsell-100-hue-color-vision-test/#prettyPhoto (accessed on 3 April 2020).
- Joint, I.S.O. CIE Standard Illuminants for Colorimetry. ISO 1999, 10526, 005. [Google Scholar]
- Nickerson, D. History of the Munsell color system and its scientific application. JOSA 1940, 30, 575–586. [Google Scholar] [CrossRef]
- Hård, A.; Sivik, L. NCS—Natural Color System: A Swedish standard for coloer notation. Color Res. Appl. 1981, 6, 129–138. [Google Scholar] [CrossRef]
- Sutton, T.; Whelan, B.M. The Complete Color Harmony, Pantone Edition: Expert Color Information for Professional Color Results; Rockport Publishers: Beberly, MA, USA, 2017. [Google Scholar]
- Stokes, M.; Anderson, M.; Chandrasekar, S.; Motta, R. A Standard Default Color Space for the Internet-Srgb. Available online: https://www.w3.org/Graphics/Color/sRGB (accessed on 3 April 2020).
- Arad, B.; Ben-Shahar, O. Sparse recovery of hyperspectral signal from natural RGB images. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 11–14 October 2016. [Google Scholar]
- Clark, J.H. The Ishihara test for color blindness. Am. J. Physiol. Opt. 1924, 5, 269–276. [Google Scholar]
- Resonon, Resonon Inc. 2019. Available online: https://resonon.com/Pika-L (accessed on 2 March 2020).
- Davidoff, C.; Neitz, M.; Neitz, J. Genetic testing as a new standard for clinical diagnosis of color vision deficiencies. Transl. Vis. Sci. Technol. 2016, 5, 2. [Google Scholar] [CrossRef] [Green Version]
- Fairman, H.S.; Brill, M.H.; Hemmendinger, H. How the CIE 1931 color-matching functions were derived from Wright-Guild data. Color Res. Appl. 1997, 22, 11–23. [Google Scholar] [CrossRef]
- Mokrzycki, W.S.; Tatol, M. Colour difference∆ E-A survey. Mach. Graph. Vis. 2011, 20, 383–411. [Google Scholar]
- Vingrys, A.J.; King-Smith, P.E. A quantitative scoring technique for panel tests of color vision. Investig. Ophthalmol. Vis. Sci. 1988, 29, 50–63. [Google Scholar]









| Observer | Filter Type | NODC Filterless (D1) | NODC Filtered (D1) | ΔNODC (D1) (%) | NODC Filterless (D2) | NODC Filtered (D2) | ΔNODC (D2) (%) |
|---|---|---|---|---|---|---|---|
| Normal | Double notch | 4192 | 4195 | 0.08 | 30,689 | 29,967 | −2.35 |
| Protan d = 0.7 | Double notch | 4061 | 4093 | 0.79 | 16,024 | 15,867 | −0.98 |
| Protan d = 1 | Double band-pass | 2855 | 2919 | 2.24 | 2634 | 2685 | 1.94 |
| Deutan d = 0.9 | Double notch | 3836 | 3866 | 0.78 | 7690 | 7686 | −0.05 |
| Deutan d = 1 | Double notch | 2993 | 3078 | 2.84 | 3176 | 3238 | 1.95 |
| Observer | Global (%) | Notch 1 (%) | Pass 1 (%) | Notch 2 (%) | Pass 2 (%) |
|---|---|---|---|---|---|
| Normal | 0.01 | 0 | 0 | 0.02 | 0 |
| Protan d = 0.7 | 0.79 | 5.18 | 0 | 0.43 | 0 |
| Protan d = 1 | 3.04 | 18.45 | 0 | 4.47 | 0.13 |
| Deutan d = 0.9 | 0.23 | 4.85 | 0 | 0.43 | 0 |
| Deutan d = 1 | 2.39 | 18.45 | 0 | 4.47 | 0.22 |
| Observer | NODC Unfiltered | NODC with EnChroma | ΔNODC EnChroma (%) | NODC with VINO | ΔNODC VINO (%) |
|---|---|---|---|---|---|
| Normal | 4192 | 4168 | −0.57 | 3934 | −6.15 |
| Protan d = 0.7 | 4061 | 3980 | −1.99 | 3735 | −8.03 |
| Protan d = 1 | 2855 | 2578 | −9.70 | 1549 | −45.74 |
| Deutan d = 0.9 | 3836 | 3680 | −4.07 | 2849 | −25.73 |
| Deutan d = 1 | 2993 | 2676 | −10.59 | 2323 | −22.39 |
| D1 | D2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Observer | ΔL* | Δa* | Δb* | ΔC* | Δhab | ΔL* | Δa* | Δb* | ΔC* | Δhab |
| Normal | −0.23 | −3.55 | 3.25 | 0.55 | −0.13 | −0.20 | −2.52 | 2.11 | 1.40 | 7.96 |
| (0.12) | (1.06) | (0.95) | (3.47) | (28.04) | (0.08) | (0.36) | (0.28) | (1.15) | (19.02) | |
| Protan d = 0.7 | −5.36 | 2.82 | −3.55 | 0.72 | −11.10 | −4.39 | 2.20 | −2.65 | −1.25 | −15.33 |
| (1.27) | (1) | (1.31) | (3.63) | (18.21) | (0.86) | (0.41) | (0.34) | (1.52) | (8.59) | |
| Protan d = 1 | −3.29 | 1.13 | −4.29 | 0.32 | 13.84 | −2.48 | 0.63 | −3.11 | −2.24 | −10.87 |
| (1.16) | (0.71) | (1.78) | (3.75) | (14.00) | (0.55) | (0.21) | (0.75) | (1.57) | (9.70) | |
| Deutan d = 0.9 | −0.09 | −0.65 | 1.88 | −0.01 | 5.63 | −0.06 | −0.36 | 1.24 | 0.94 | 3.6 |
| (0.04) | (0.29) | (0.5) | (1.69) | (6.61) | (0.01) | (0.08) | (0.12) | (0.61) | (3.48) | |
| Deutan d = 1 | −4.13 | 1.69 | −5.97 | 1.11 | −14.55 | −2.98 | 0.89 | −4.24 | −2.85 | −14.77 |
| (1.63) | (1.13) | (2.52) | (5.63) | (16.86) | (0.6) | (0.28) | (0.89) | (2.37) | (14.31) | |
| Observer | SQR (unfilt) | SQR (filt) | Angle (unfilt) | Angle (filt) | CI (unfilt) | CI (filt) | SI (unfilt) | SI (filt) |
|---|---|---|---|---|---|---|---|---|
| Normal | 2 | 2 | 49.58 | 49.58 | 1.05 | 1.05 | 1.33 | 1.33 |
| Protan d = 0.7 | 6 | 12.96 | 61.47 | 54.14 | 1.28 | 2.4 | 1.46 | 1.3 |
| Protan d = 1 | 17.55 | 19.80 | 43.17 | 42.52 | 5.89 | 5.03 | 2.07 | 1.85 |
| Deutan d = 0.9 | 15.23 | 15.62 | 43.3 | 46.32 | 4.61 | 4.47 | 1.64 | 1.63 |
| Deutan d = 1 | 16.97 | 17.32 | 48.72 | 56.17 | 3.95 | 3.7 | 1.45 | 1.27 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez-Domingo, M.Á.; Valero, E.M.; Gómez-Robledo, L.; Huertas, R.; Hernández-Andrés, J. Spectral Filter Selection for Increasing Chromatic Diversity in CVD Subjects. Sensors 2020, 20, 2023. https://doi.org/10.3390/s20072023
Martínez-Domingo MÁ, Valero EM, Gómez-Robledo L, Huertas R, Hernández-Andrés J. Spectral Filter Selection for Increasing Chromatic Diversity in CVD Subjects. Sensors. 2020; 20(7):2023. https://doi.org/10.3390/s20072023
Chicago/Turabian StyleMartínez-Domingo, Miguel Ángel, Eva M. Valero, Luis Gómez-Robledo, Rafael Huertas, and Javier Hernández-Andrés. 2020. "Spectral Filter Selection for Increasing Chromatic Diversity in CVD Subjects" Sensors 20, no. 7: 2023. https://doi.org/10.3390/s20072023
APA StyleMartínez-Domingo, M. Á., Valero, E. M., Gómez-Robledo, L., Huertas, R., & Hernández-Andrés, J. (2020). Spectral Filter Selection for Increasing Chromatic Diversity in CVD Subjects. Sensors, 20(7), 2023. https://doi.org/10.3390/s20072023









