Application of Multi-Branch Cauer Circuits in the Analysis of Electromagnetic Transducers Used in Wireless Transfer Power Systems
Abstract
:1. Introduction
2. Equivalent Model Based on Multi-Branch Cauer Circuits
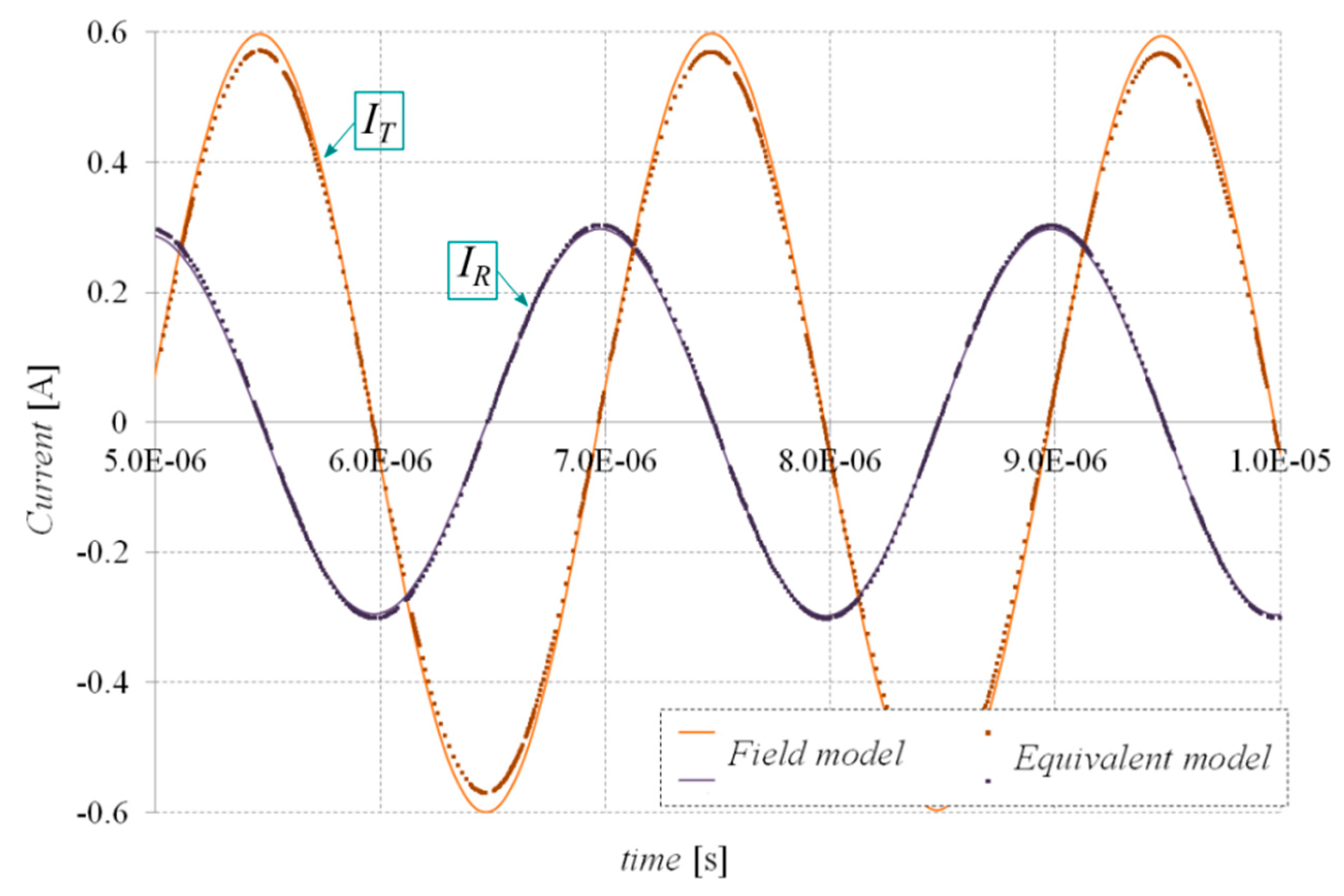
3. Results
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Duncan, K.J. Laser based power transmission: Component selection and laser hazard analysis. In Proceedings of the 2016 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), Knoxville, TN, USA, 4–6 October 2016; pp. 100–103. [Google Scholar]
- Wang, N.; Zhu, Y.; Wei, W.; Chen, J.; Liu, S.; Li, P.; Wen, Y. One-to-Multipoint Laser Remote Power Supply System for Wireless Sensor Networks. IEEE Sens. J. 2011, 12, 389–396. [Google Scholar] [CrossRef]
- Wagih, M.; Komolafe, A.; Zaghari, B. Separation-Independent Wearable 6.78 MHz Near-Field Radiative Wireless Power Transfer using Electrically Small Embroidered Textile Coils. Energies 2020, 13, 528. [Google Scholar] [CrossRef] [Green Version]
- Jang, Y.; Jovanovic, M. A contactless electrical energy transmission system for portable-telephone battery chargers. IEEE Trans. Ind. Electron. 2003, 50, 520–527. [Google Scholar] [CrossRef] [Green Version]
- Choi, B.; Nho, J.; Cha, H.; Ahn, T.; Choi, S. Design and Implementation of Low-Profile Contactless Battery Charger Using Planar Printed Circuit Board Windings as Energy Transfer Device. IEEE Trans. Ind. Electron. 2004, 51, 140–147. [Google Scholar] [CrossRef] [Green Version]
- Maradewicz, A.; Kaźmierkowski, M.P. Resonant converter based contactless power supply for robots and manipulators. J. Autom. Mobile Robot. Intell. Syst. 2008, 2, 20–25. [Google Scholar]
- Lee, S.-Y.; Cheng, C.-J.; Liang, M.-C. A Low-Power Bidirectional Telemetry Device with a Near-Field Charging Feature for a Cardiac Microstimulator. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 357–367. [Google Scholar] [CrossRef]
- Cheong, J.H.; Ng, S.S.Y.; Liu, X.; Xue, R.-F.; Lim, H.J.; Khannur, P.B.; Chan, K.L.; Lee, A.A.; Kang, K.; Lim, L.S.; et al. An Inductively Powered Implantable Blood Flow Sensor Microsystem for Vascular Grafts. IEEE Trans. Biomed. Eng. 2012, 59, 2466–2475. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Peng, F.; Li, Y.; Yang, T.; Wang, B.; Fang, D. A Wireless Magnetic Resonance Energy Transfer System for Micro Implantable Medical Sensors. Sensors 2012, 12, 10292–10308. [Google Scholar] [CrossRef]
- Song, S.; Zhang, Q.; Zhu, C.; Wang, D. A practical static simulator for dynamic wireless charging of electric vehicle using receiver open circuit voltage equivalent. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 4859–4864. [Google Scholar]
- Alam Chowdhury, M.S.; Liang, X. Design of a Ferrite-Less Power Pad for Wireless Charging Systems of Electric Vehicles. In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; pp. 1–4. [Google Scholar]
- Hurley, W.; Duffy, M. Calculation of self and mutual impedances in planar magnetic structures. IEEE Trans. Magn. 1995, 31, 2416–2422. [Google Scholar] [CrossRef]
- Dai, W.; Tang, W.; Cai, C.; Deng, L.; Zhang, X. Wireless Power Charger Based on Class E Amplifier with the Maximum Power Point Load Consideration. Energies 2018, 11, 2378. [Google Scholar] [CrossRef] [Green Version]
- Olukotun, B.; Partridge, J.; Bucknall, R. Finite Element Modeling and Analysis of High Power, Low-loss Flux-Pipe Resonant Coils for Static Bidirectional Wireless Power Transfer. Energies 2019, 12, 3534. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhao, Y.; Ho, S.L.; Fu, W. Analysis of Wireless Power Transfer System Based on 3-D Finite-Element Method Including Displacement Current. IEEE Trans. Magn. 2012, 48, 3692–3695. [Google Scholar] [CrossRef]
- Demenko, A.; Wojciechowski, R.M.; Sykulski, J. 2-D Versus 3-D Electromagnetic Field Modeling in Electromechanical Energy Converters. IEEE Trans. Magn. 2014, 50, 897–900. [Google Scholar] [CrossRef]
- Shimotani, T.; Sato, Y.; Igarashi, H. Equivalent-Circuit Generation from Finite-Element Solution Using Proper Orthogonal Decomposition. IEEE Trans. Magn. 2015, 52, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Kurzawa, M.; Jedryczka, C.; Wojciechowski, R.M. Analysis of Eddy Current System using Equivalent Multi-Branch Foster Circuit and Edge Element Method. In Proceedings of the 19th International Conference Computational Problems of Electrical Engineering, Banská Štiavnica, Slovak Republic, 9–12 September 2018; pp. 1–4. [Google Scholar]
- Demenko, A.; Sykulski, J.; Wojciechowski, R. Network Representation of Conducting Regions in 3-D Finite-Element Description of Electrical Machines. IEEE Trans. Magn. 2008, 44, 714–717. [Google Scholar] [CrossRef] [Green Version]
- Demenko, A.; Sykulski, J. Magneto-electric network models in electromagnetism. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2006, 25, 581–588. [Google Scholar] [CrossRef] [Green Version]
- Demenko, A.; Wojciechowski, R.; Sykulski, J. Calculation of inducted currents using edge elements and T–T0 formulation. IET Sci. Meas. Technol. 2008, 2, 434–439. [Google Scholar] [CrossRef] [Green Version]
- Wojciechowski, R.; Demenko, A.; Sykulski, J. Inducted currents analysis in multiply connected conductors using reluctance-resistance networks. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2010, 29, 908–918. [Google Scholar] [CrossRef]
- Wojciechowski, R.; Jedryczka, C.; Szelag, W.; Demenko, A. Description of multiply connected regions with induced currents using T-T0 method. Prog. Electromagn. Res. B 2012, 43, 279–294. [Google Scholar] [CrossRef] [Green Version]
- Wojciechowski, R.; Demenko, A.; Sykulski, J. Comparative analysis of A−V and A−T−T0 calculations of induced currents in multiply connected regions. IET Sci. Meas. Technol. 2012, 6, 312. [Google Scholar] [CrossRef] [Green Version]
- Wojciechowski, R.M.; Kurzawa, M.; Jędryczka, C. Application of evolution strategy to determine the parameters of the multi-branch Foster and Cauer Circuit of Eddy current system. In Proceedings of the Symposium on Electromagnetic Phenomena in Nonlinear Circuits 2018, Arras, France, 26–29 June 2018; pp. 1–2. [Google Scholar]
- Kurzawa, M.; Wojciechowski, R.M. The system of wireless power transmission containing the serial-parallel resonant circuit in cooperation with the bridge voltage inverter. Poznan Univ. Technol. Acad. J. Electr. Eng. 2017, 90, 301–312. (In Polish) [Google Scholar]
- Feldmann, P.; Freund, R. Efficient linear circuit analysis by Pade approximation via the Lanczos process. IEEE Trans. Comput. Des. Integr. Circuits Syst. 1995, 14, 639–649. [Google Scholar] [CrossRef]
- Shimotani, T.; Sato, Y.; Igarashi, H. Direct synthesis of equivalent circuits from reduced FE models using proper orthogonal decomposition. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 2035–2044. [Google Scholar] [CrossRef]



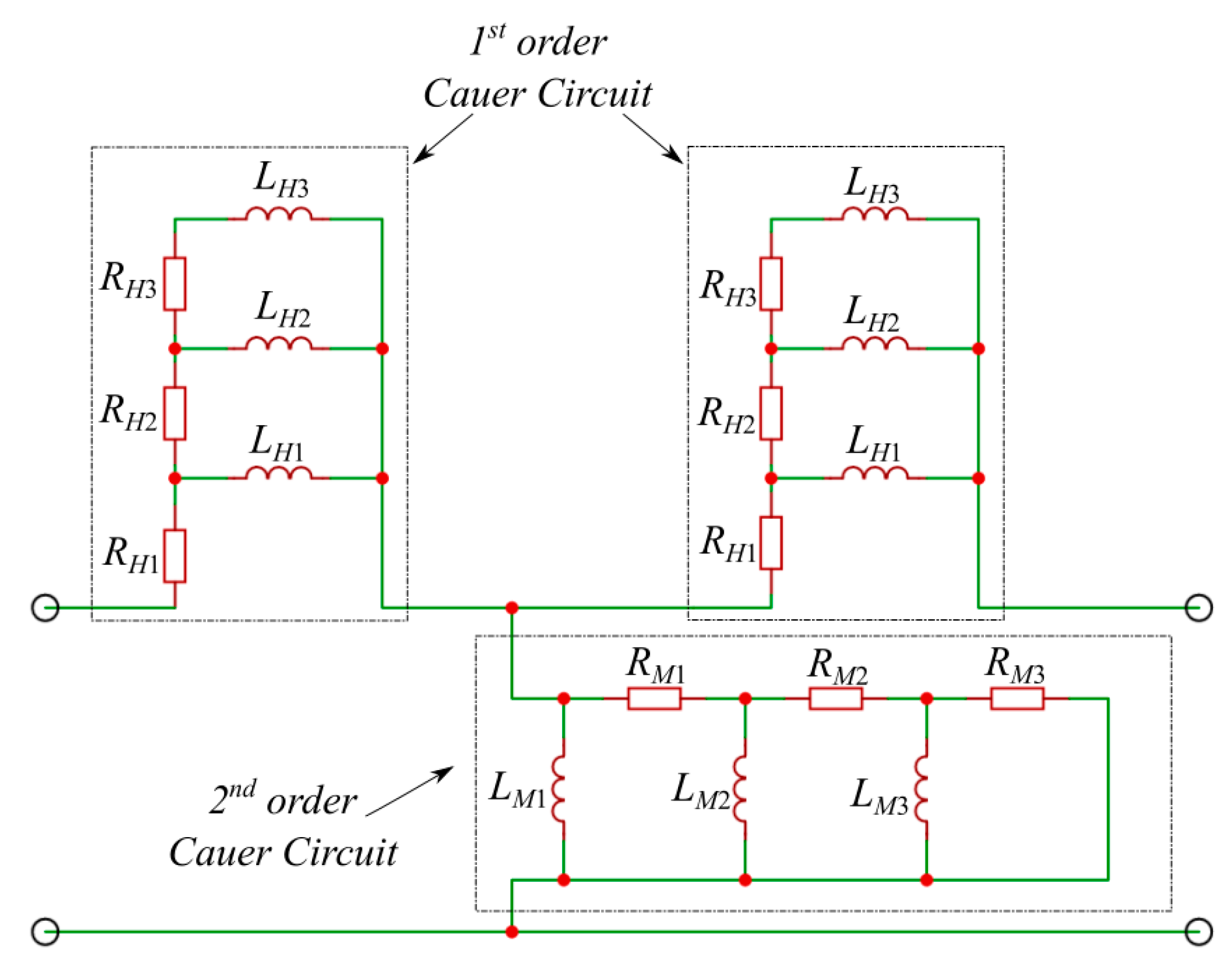



| RH1 [Ω] | RH2 [Ω] | RH3 [Ω] |
| 0.176 | 1450.0 | 1837.0 |
| LH1 [μH] | LH2 [mH] | LH3 [mH] |
| 12.065 | 154.170 | 3.651 |
| RM1 [Ω] | RM2 [Ω] | RM3 [Ω] |
| 1300.34 | 34.516 | 3.141·109 |
| LM1 [μH] | LM2 [mH] | LM3 [mH] |
| 21.239 | 572.919 | 4.928 |
| Frequency | ||
|---|---|---|
| 500 kHz | 0.0469 | 0.0198 |
| 1 MHz | 0.0217 | 0.0363 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurzawa, M.; Jędryczka, C.; Wojciechowski, R.M. Application of Multi-Branch Cauer Circuits in the Analysis of Electromagnetic Transducers Used in Wireless Transfer Power Systems. Sensors 2020, 20, 2052. https://doi.org/10.3390/s20072052
Kurzawa M, Jędryczka C, Wojciechowski RM. Application of Multi-Branch Cauer Circuits in the Analysis of Electromagnetic Transducers Used in Wireless Transfer Power Systems. Sensors. 2020; 20(7):2052. https://doi.org/10.3390/s20072052
Chicago/Turabian StyleKurzawa, Milena, Cezary Jędryczka, and Rafał M. Wojciechowski. 2020. "Application of Multi-Branch Cauer Circuits in the Analysis of Electromagnetic Transducers Used in Wireless Transfer Power Systems" Sensors 20, no. 7: 2052. https://doi.org/10.3390/s20072052
APA StyleKurzawa, M., Jędryczka, C., & Wojciechowski, R. M. (2020). Application of Multi-Branch Cauer Circuits in the Analysis of Electromagnetic Transducers Used in Wireless Transfer Power Systems. Sensors, 20(7), 2052. https://doi.org/10.3390/s20072052





