Automatic Calibration of the Step Length Model of a Pocket INS by Means of a Foot Inertial Sensor
Abstract
:1. Introduction
- by means of a step length model, which is an equation that relates observable parameters, e.g., the acceleration [10], with the step length. The advantage of this alternative is that we can gain an understanding of how the observable parameters relate to the step length model. Moreover, the implementation of step length models has a low computational complexity and therefore can be implemented in wearables or smartphones. The disadvantage of this alternative is that the step length model contains parameters which need to be adapted or tuned to the pedestrian.
- by means of leg kinematics, which is a method that develops a kinematic model of the human leg and uses kinematic equations to iteratively detect steps and estimate the step length between two consecutive steps [11]. The advantage of this alternative is that it is possible to incorporate motion constraints in the kinematic model. The disadvantage is that the motion constraints may lead to unexpected results. In addition, the development of a kinematic model is a complex process.
- by means of machine learning methods, which take observable signals like the acceleration and turn rate and the associated step length and train an algorithm to estimate the step length [12]. The advantage of this alternative is that the machine learning method needs to be trained only once. The disadvantage is that it is necessary to collect a large data set, e.g., hundreds of users, to train the network. Moreover, some machine learning algorithms are computationally expensive and thus cannot be implemented in wearables or smartphones.
- the use of trained parameters [14], which is the most common calibration approach. These parameters are learned by training the step length model with the data from a set of users. The main challenge of this alternative is that the data set has to be large and varied in order for the parameters to be meaningful. A large data set refers to the number of users, e.g., a data set with data from a few hundred users. To the best of our knowledge, there is no work that recommends a minimum number of volunteers for such a training. A varied data set refers to the fact that the data should be from users of different gender, height, physical constitution, etc. The disadvantage of this calibration method is that it fails to optimally characterize the step length model to a specific user. Thus, the step length model will have a systematic error in its estimation.
- manual calibration [15]. In this method, the user is required to walk a predefined known distance. Then, the user or an external operator estimates an average step length by dividing the predefined distance by the number of steps. Finally, the model parameters are calibrated to estimate the average step length. The shortcoming of this alternative is that it is prone to errors, if the person who carries out the calibration is not familiar with the system. In addition, it is necessary to measure a predefined distance, which may be another source of errors. Manual calibration can be carried out without the need to manually measure distances. To that end, maps can be used to calculate the distance that the user walks [16]. The disadvantage of this alternative is the reliance on the availability of maps, which may not be available or may contain wrong information.
- the pedestrian uses the inertial localization system for the first time,
- the IMU is placed on the expected body location, e.g., the upper thigh, but the exact position of the IMU is shifted with respect to the last time the calibration was carried out or
- the IMU slips during the walk.
- identify if it is necessary to calibrate all the parameters of the step length model of an IMU mounted on the upper thigh,
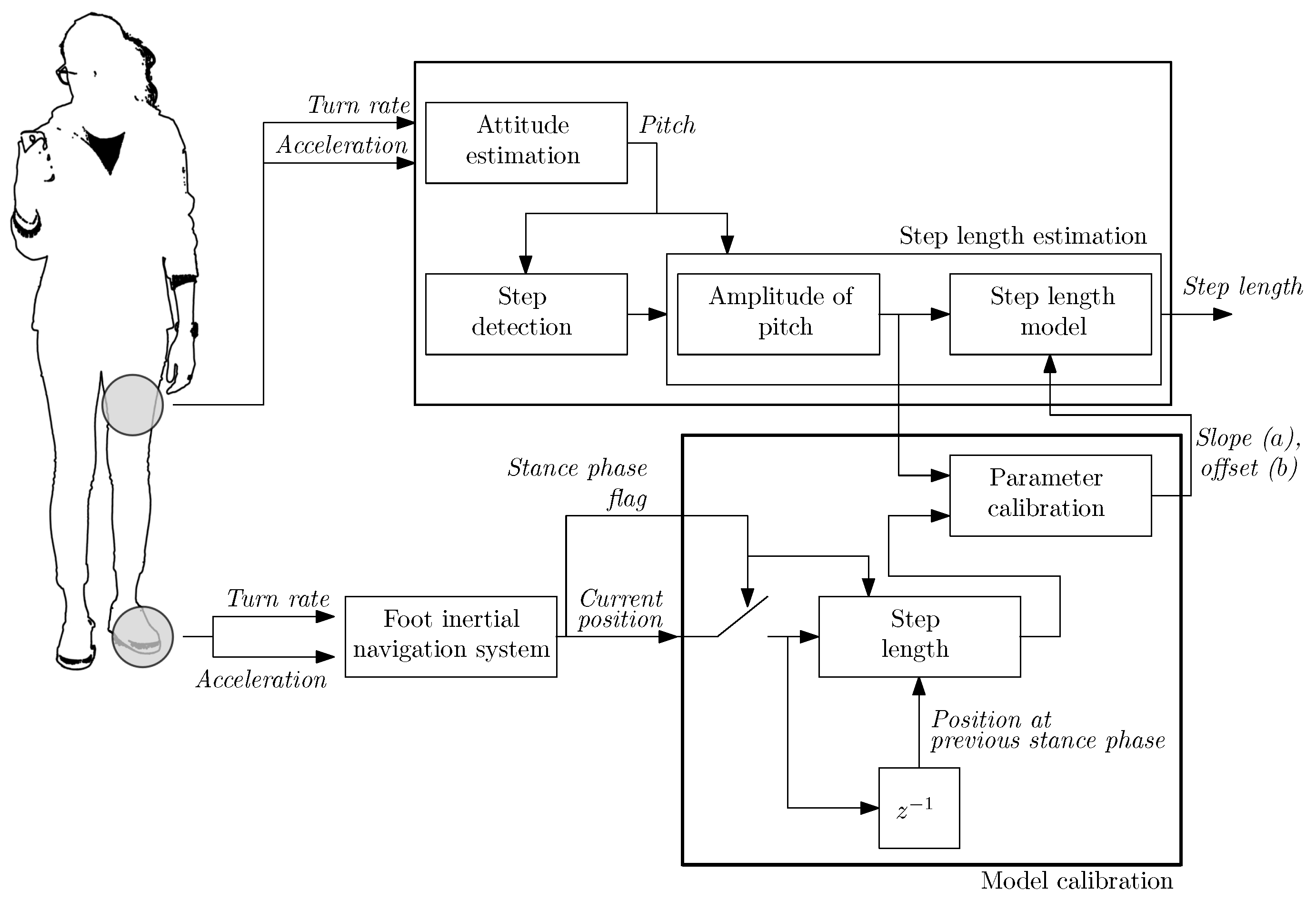
- develop an automatic calibration method based on a foot IMU,
- quantitatively evaluate the performance of the pocket INS with the proposed calibration method and compare it to the performance of the pocket INS without automatic calibration.
2. Materials and Methods
- two IMUs are fixed on the same leg of the user and they do not move during the walk, see left picture in Figure 1,
- one IMU is mounted on the upper-thigh, and
- one IMU is mounted on the front part of the foot.
2.1. Fundamental Concepts
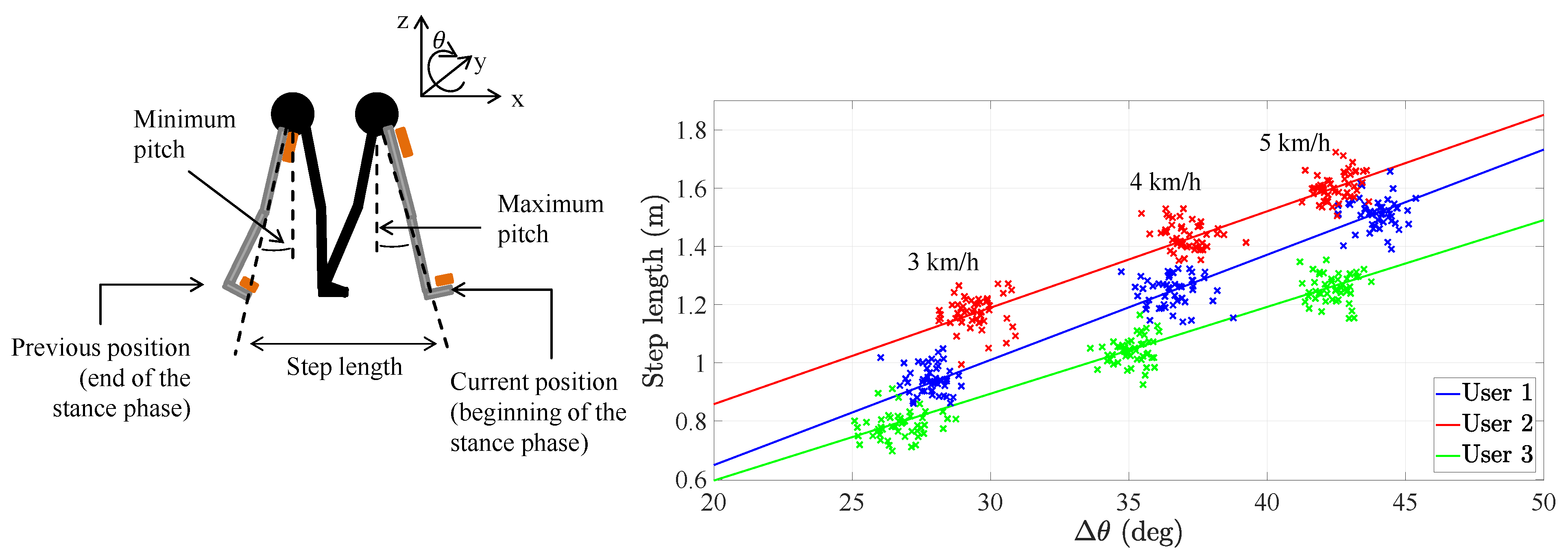
2.1.1. Step Length Model of a Pocket INS
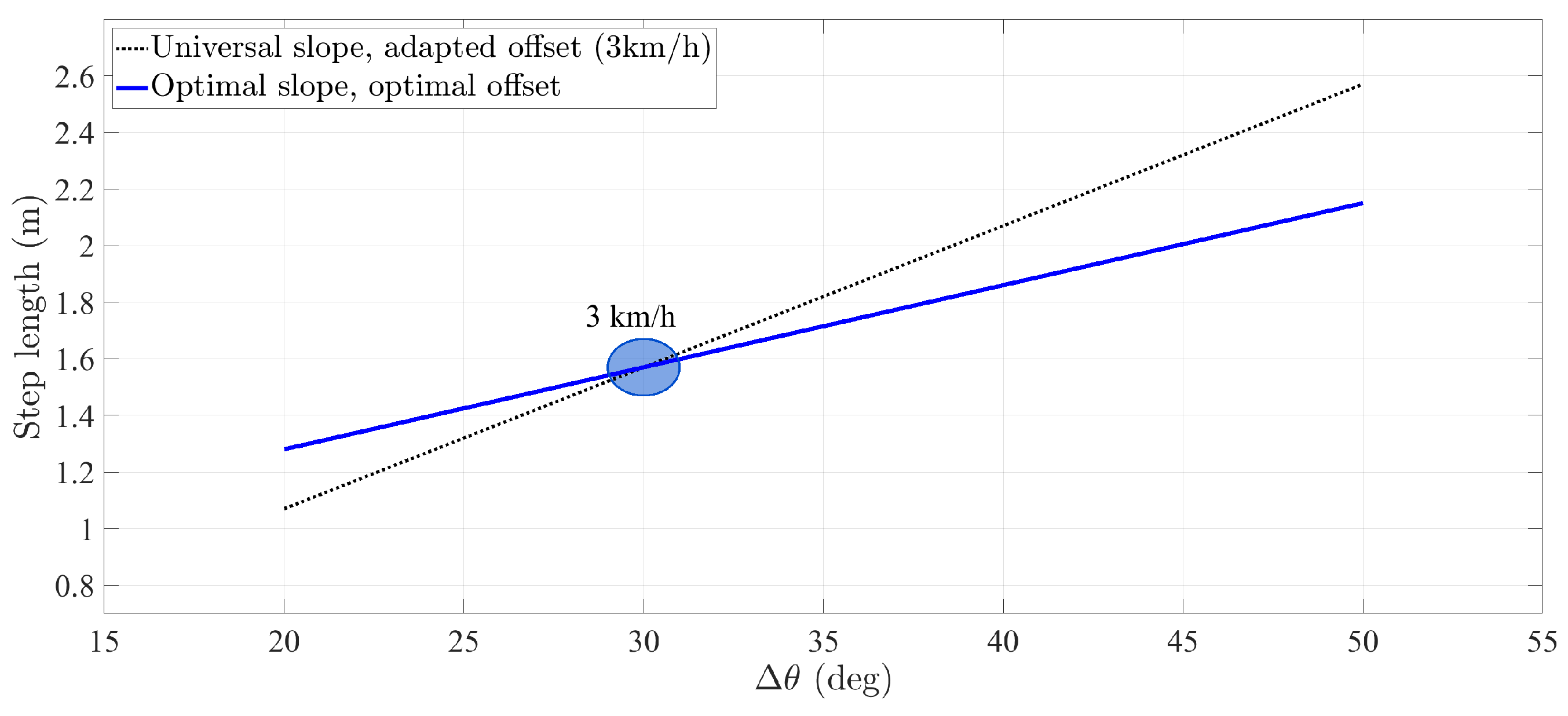
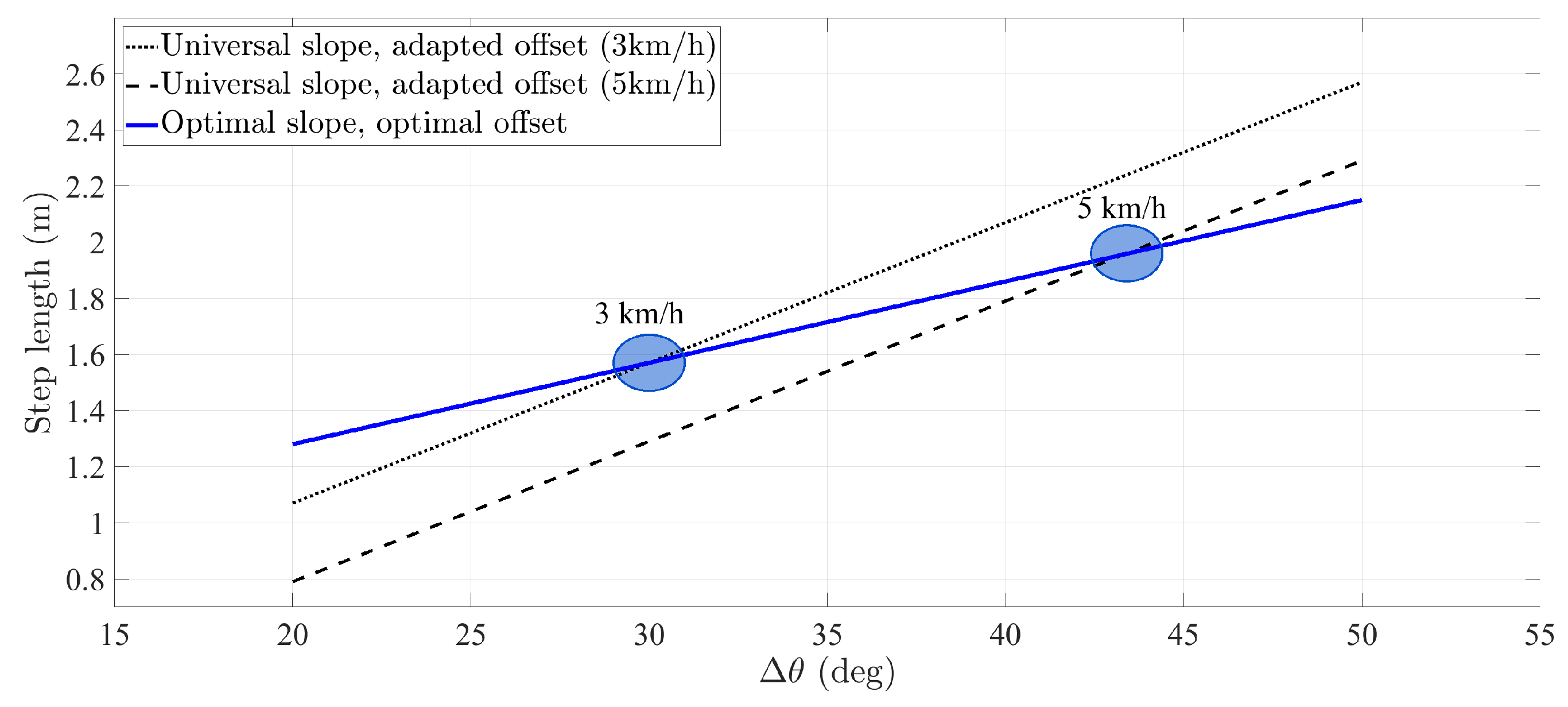
- The first alternative is the offset calibration, which implements the universal slope a and calibrates the offset b to every user. The universal slope is the value obtained after training the parameters on a set of users, namely 0.05 m/° [15]. This calibration method assumes that the user’s slope equals the universal slope, which may not be a valid assumption for certain users.
- The second alternative is the full calibration, which estimates the user’s optimal slope and optimal offset by following the methodology described in [18]. This calibration method is costly in time and resources. Firstly, it is necessary to request the user to actively change the walking speed in order to obtain values along the line in Figure 1. Secondly, it is necessary to estimate the parameters of the step length model in a post-processing stage. Finally, it may still be necessary to adjust the offset b if the inertial sensor is not placed on the same position along the leg [17].
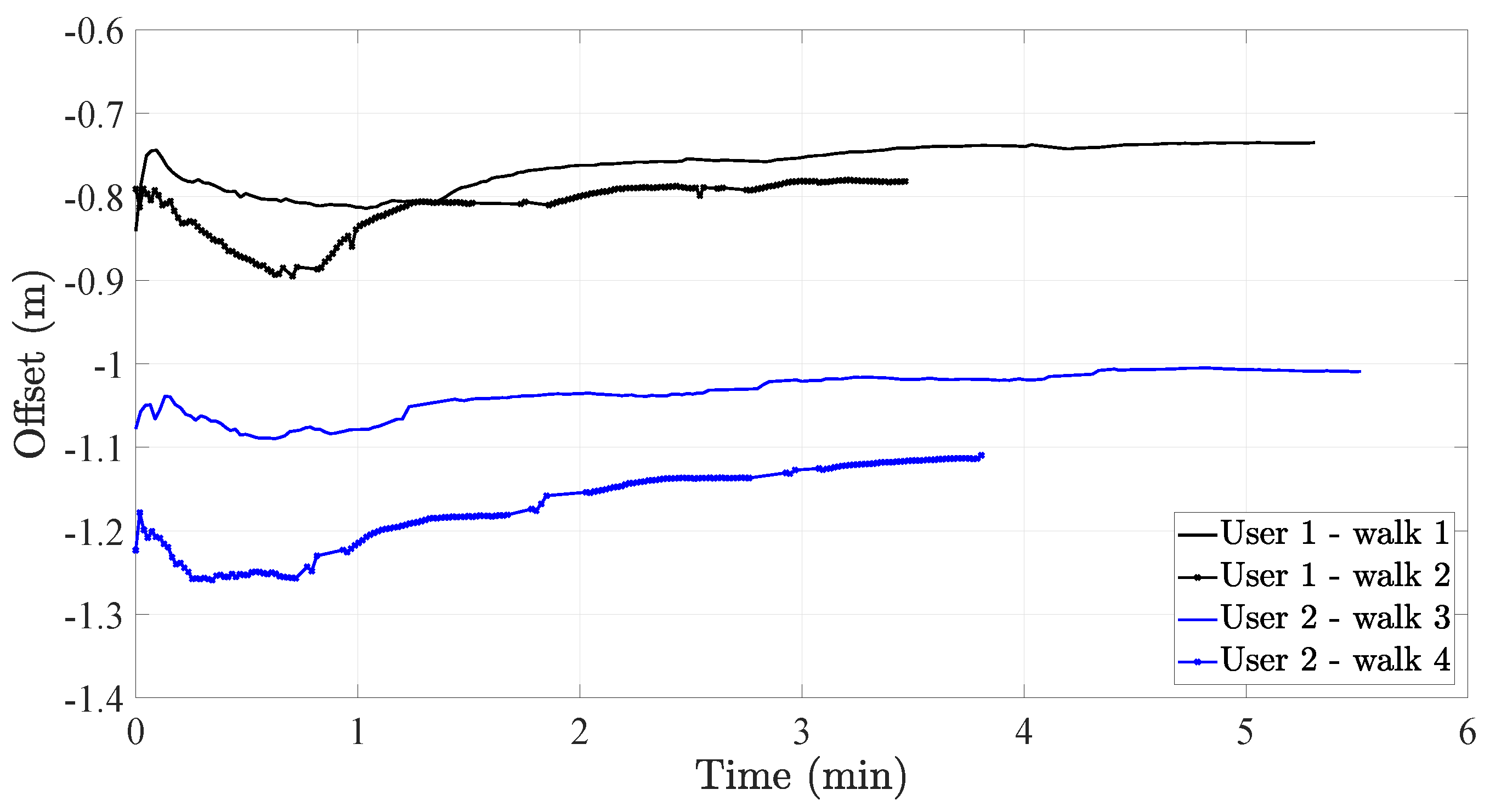
2.1.2. Automatic Offset Calibration
2.2. Analysis of the Need for Full Calibration of the Step Length Model
2.3. Automatic Full Calibration of the Step Length Model
2.4. Practical Implementation
3. Results
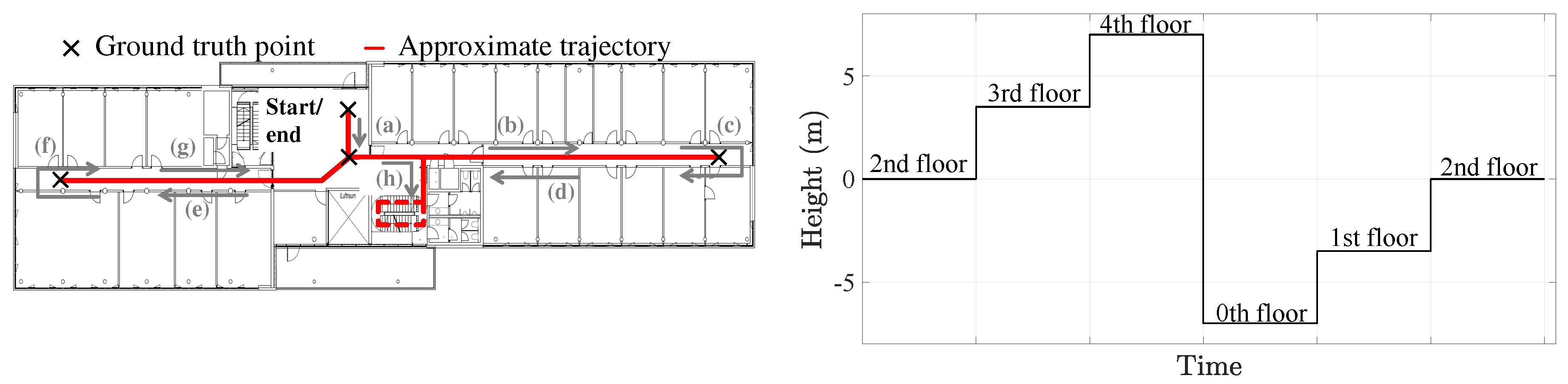
3.1. Evaluation Methodology
- The users visited each of the five floors in the sequence indicated by the height profile in Figure 9, i.e., they started in the second floor, then proceeded to the third floor by taking the stairs, etc.
- The users always took the stairs during the experiments.
- In each floor, the users walked the trajectory indicated on the left picture of Figure 9.
- the user starts on the second floor, at the point indicated on the right picture of Figure 9,
- the user follows the sequence indicated by the letters (a)–(h) on the left picture of Figure 9,
- on the new floor, the users follow the trajectory (b)–(h). For each floor, the user repeats phases 3 and 4 until the user is back to the end point on the second floor.
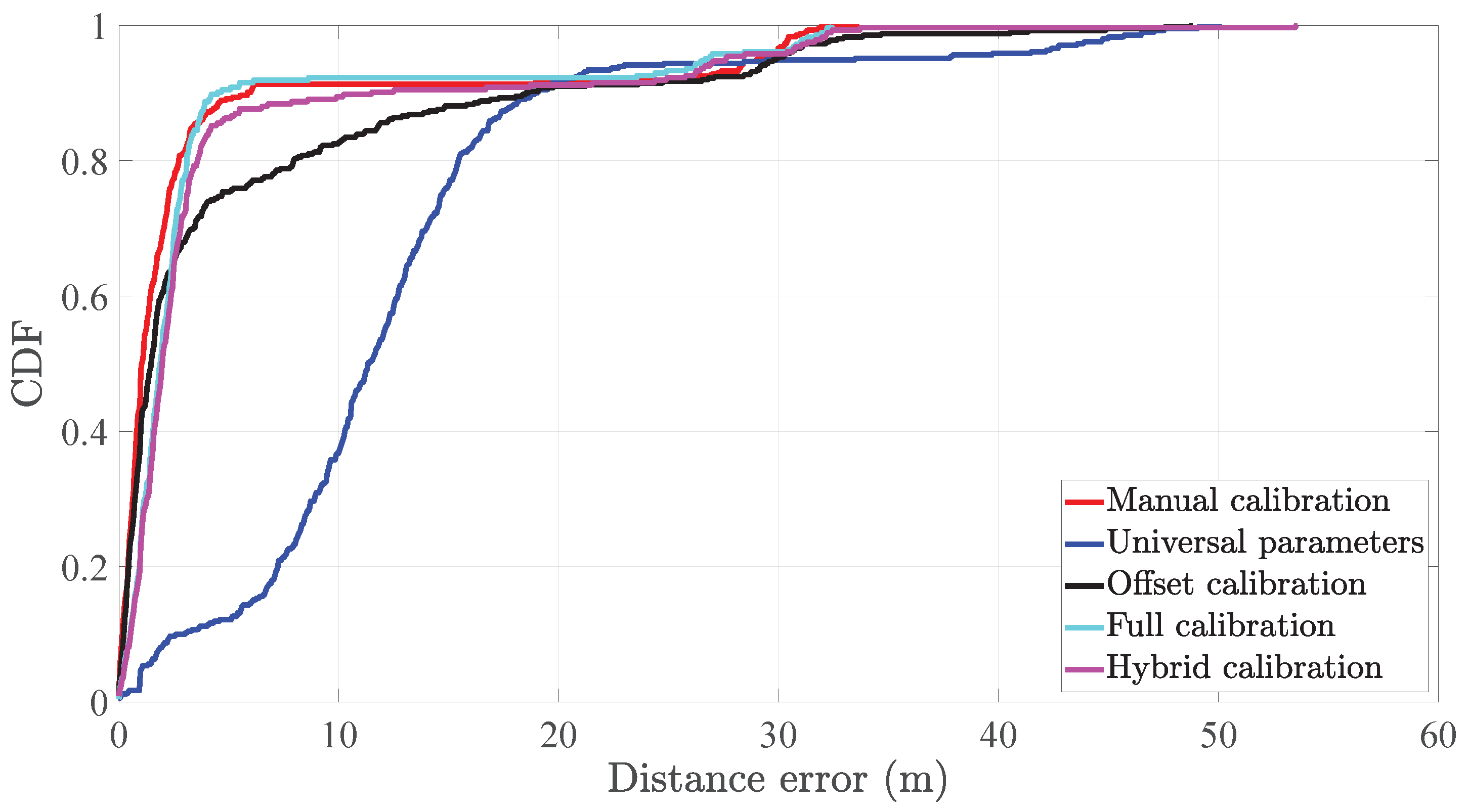
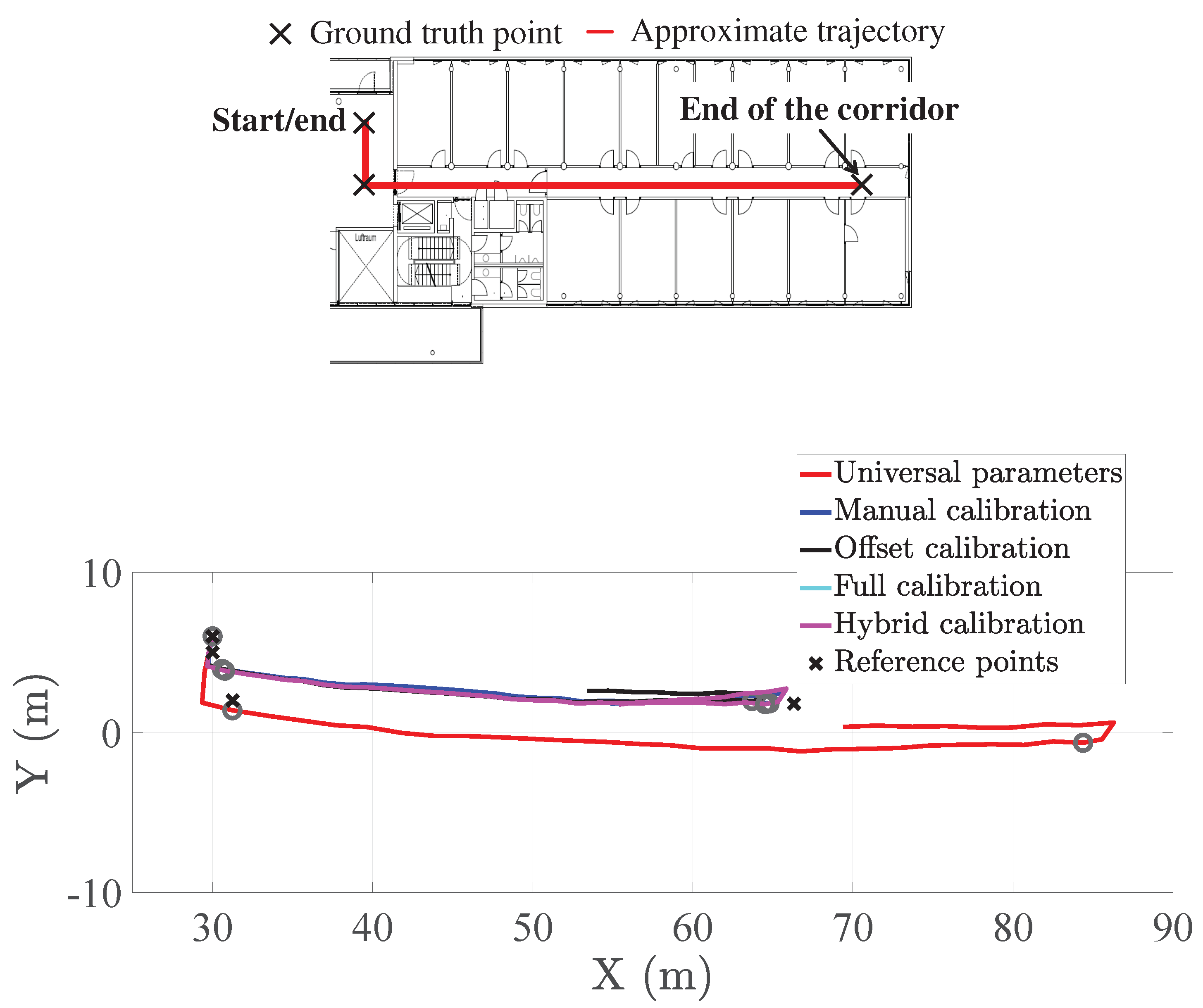
3.2. Results and Discussion
- in the first one, the step length model implements the universal parameters [15]. In the following, we refer to this implementation of the pocket INS as universal parameters.
- in the second one, the step length model is manually calibrated to each user [15]. In the following, we refer to this implementation of the pocket INS as manual calibration.
- in the third one, only the offset of the step length model is automatically calibrated while the slope is set to the universal value, namely 0.05 m/°, see Section 2.1.2. In the following, we refer to this implementation of the pocket INS as offset calibration.
- the first set of parameters comprises the ones indicated in Table 2. In the following, we refer to this implementation of the pocket INS as full calibration.
- the second set of parameters comprises the user’s optimal slope, estimated with the proposed method, whereas the offset is calibrated with Equation (2). For the implementation of Equation (2), we have set the slope a to the user’s optimal value, see Table 2. In the following, we refer to this implementation of the pocket INS as hybrid calibration.
- with respect to the full calibration, the hybrid calibration benefits from using the user’s optimal slope which clearly outperforms the offset calibration, see Table 3.
- with respect to the offset calibration, the hybrid calibration benefits from the fact that it is only necessary at the beginning of the walk and it is a process transparent to the user [17].
4. Conclusions
5. Patents
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| IMU | Inertial Measurement Unit |
| INS | Inertial Navigation System |
| ZUPT | Zero-velocity UPdaTe |
| CDF | Cumulative Distribution Function |
References
- Polo, A.; Viani, F.; Giarola, E.; Oliveri, G.; Rocca, P.; Massa, A. Semantic wireless localization enabling advanced services in museums. In Proceedings of the 8th European Conference on Antennas and Propagation (EuCAP 2014), The Hague, Netherlands, 6–11 April 2014. [Google Scholar] [CrossRef]
- Chianese, A.; Marulli, F.; Moscato, V.; Piccialli, F. SmARTweet: A location-based smart application for exhibits and museums. In Proceedings of the 2013 International Conference on Signal-Image Technology & Internet-Based Systems, Kyoto, Japan, 2–5 December 2013. [Google Scholar] [CrossRef]
- Nilsson, J.O.; Rantakokko, J.; Handel, P.; Skog, I.; Ohlsson, M.; Hari, K. Accurate indoor positioning of firefighters using dual foot-mounted inertial sensors and inter-agent ranging. In Proceedings of the 2014 IEEE/ION Position, Location and Navigation Symposium - PLANS 2014, Monterey, CA, USA, 5–8 May 2014. [Google Scholar] [CrossRef] [Green Version]
- Bousdar Ahmed, D.; Munoz Diaz, E.; Kaiser, S. Performance comparison of foot- and pocket-mounted inertial navigation systems. In Proceedings of the 2016 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Spain, 4–7 October 2016. [Google Scholar] [CrossRef]
- Bousdar Ahmed, D.; Diez Blanco, L.E.; Munoz Diaz, E. Performance comparison of wearable-based pedestrian navigation systems in large areas. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017. [Google Scholar] [CrossRef] [Green Version]
- Gu, F.; Khoshelham, K.; Shang, J.; Yu, F.; Wei, Z. Robust and accurate smartphone-based step counting for indoor localization. IEEE Sens. J. 2017, 17, 3453–3460. [Google Scholar] [CrossRef]
- Xu, L.; Xiong, Z.; Liu, J.; Wang, Z.; Ding, Y. A novel pedestrian dead reckoning algorithm for multi-mode recognition based on smartphones. Remote Sens. 2019, 11, 294. [Google Scholar] [CrossRef] [Green Version]
- Woodman, O.J. An Introduction to Inertial Navigation; Technical Report; Computer Laboratory, University of Cambridge: Cambridge, UK, 2007. [Google Scholar]
- Conesa, J.; Pérez-Navarro, A.; Torres-Sospedra, J.; Montoliu, R. Geographical and Fingerprinting Data for Positioning and Navigation Systems: Challenges, Experiences and Technology Roadmap (Intelligent Data-Centric Systems: Sensor Collected Intelligence), 1st ed.; Academic Press: London, UK, 2018; Chapter 16. [Google Scholar]
- Diez, L.E.; Bahillo, A.; Otegui, J.; Otim, T. Step length estimation methods based on inertial sensors: A review. IEEE Sens. J. 2018, 18, 6908–6926. [Google Scholar] [CrossRef]
- Meng, X.L.; Zhang, Z.Q.; Sun, S.Y.; Wu, J.K.; Wong, W.C. Biomechanical model-based displacement estimation in micro-sensor motion capture. Meas. Sci. Technol. 2012, 23. [Google Scholar] [CrossRef]
- Gu, F.; Khoshelham, K.; Yu, C.; Shang, J. Accurate step length estimation for pedestrian dead reckoning localization using stacked autoencoders. IEEE Trans. Instrum. Meas. 2019, 68, 2705–2713. [Google Scholar] [CrossRef]
- Munoz Diaz, E.; de Ponte Müller, F.; Domínguez, J.G. Use of the magnetic field for improving gyroscopes’ biases estimation. Sensors 2017, 17, 832. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Moder, T.; Wisiol, K.; Hafner, P.; Wieser, M. Smartphone-based indoor positioning utilizing motion recognition. In Proceedings of the 2015 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Banff, AB, Canada, 13–16 October 2015. [Google Scholar] [CrossRef]
- Munoz Diaz, E. Inertial pocket navigation system: Unaided 3D positioning. Sensors 2015, 15, 9156–9178. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alaoui, F.T.; Betaille, D.; Renaudin, V. A multi-hypothesis particle filtering approach for pedestrian dead reckoning. In Proceedings of the 2016 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Alcala de Henares, Spain, 4–7 October 2016; pp. 1–8. [Google Scholar] [CrossRef] [Green Version]
- Bousdar Ahmed, D.; Munoz Diaz, E.; Conejo Minguez, J.A. Exploiting wearable devices for the calibration of inertial navigation systems. In Proceedings of the 2017 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Sapporo, Japan, 18–21 September 2017. [Google Scholar] [CrossRef] [Green Version]
- Munoz Díaz, E.; Mendiguchía González, A.L. Step detector and step length estimator for an inertial pocket navigation system. In Proceedings of the IEEE/ION Position Location and Navigation Symposium (PLANS), Busan, Korea, 27–30 October 2014. [Google Scholar]
- Haykin, S. Adaptive Filter Theory; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1996. [Google Scholar]
- Miller, S.J. The Method of Least Squares. Available online: https://web.williams.edu/Mathematics/sjmiller/public_html/BrownClasses/54/handouts/MethodLeastSquares.pdf (accessed on 6 April 2020).
- Torres-Sospedra, J.; Jiménez, A.; Moreira, A.; Lungenstrass, T.; Lu, W.C.; Knauth, S.; Mendoza-Silva, G.; Seco, F.; Pérez-Navarro, A.; Nicolau, M.; et al. Off-line evaluation of mobile-centric indoor positioning systems: The experiences from the 2017 IPIN competition. Sensors 2018, 18, 487. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Renaudin, V.; Marbel, R.; Ben-Moshe, B.; Zheng, X.; Ye, F.; Kuang, J.; Li, Y.; Niu, X.; Landa, V.; Hacohen, S.; et al. Evaluating indoor positioning systems in a shopping mall: The lessons learned from the IPIN 2018 competition. IEEE Access 2019, 7, 148594–148628. [Google Scholar] [CrossRef]
- ISO/IEC 18305: Information Technology—Real Time Locating Systems—Test and Evaluation of Localization and Tracking Systems; International Organization for Standardization: Geneva, Switzerland, 2016.
- IPIN Competition. 2018. Available online: http://ipin2018.ifsttar.fr/fileadmin/contributeurs/IPIN2018/COMPETITION/IPIN2018_CallForCompetition_v2.1.pdf (accessed on 6 April 2020).
- Technologies, X. MTw User Manual; Xsens Technologies B.V.: Enschede, The Netherlands, 2018; pp. 14–18. [Google Scholar]




| No. of Users | Total Time | Total No. of Ground Truth Points |
|---|---|---|
| 4 | 3 h 20 min | 295 |
| User | Slope a [m/°] | Offset b [m] |
|---|---|---|
| User 1 | 0.0288 | 0.1 |
| User 2 | 0.0523 | −0.7 |
| User 3 | 0.0450 | −0.5 |
| User 4 | 0.0437 | −0.6 |
| System Description | ed [m] | Q3(ed) [m] | eψ [°] | eh [m/m] |
|---|---|---|---|---|
| Universal parameters | 14.9 | |||
| Manual calibration | 3.4 ± 7.7 | 2.3 | 61.1 ± 48.6 | 0.6 ± 1.4 |
| Offset calibration | 4.7 | |||
| Full calibration | 2.8 | |||
| Hybrid calibration | 3.1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bousdar Ahmed, D.; Diaz, E.M.; García Domínguez, J.J. Automatic Calibration of the Step Length Model of a Pocket INS by Means of a Foot Inertial Sensor. Sensors 2020, 20, 2083. https://doi.org/10.3390/s20072083
Bousdar Ahmed D, Diaz EM, García Domínguez JJ. Automatic Calibration of the Step Length Model of a Pocket INS by Means of a Foot Inertial Sensor. Sensors. 2020; 20(7):2083. https://doi.org/10.3390/s20072083
Chicago/Turabian StyleBousdar Ahmed, Dina, Estefania Munoz Diaz, and Juan Jesús García Domínguez. 2020. "Automatic Calibration of the Step Length Model of a Pocket INS by Means of a Foot Inertial Sensor" Sensors 20, no. 7: 2083. https://doi.org/10.3390/s20072083
APA StyleBousdar Ahmed, D., Diaz, E. M., & García Domínguez, J. J. (2020). Automatic Calibration of the Step Length Model of a Pocket INS by Means of a Foot Inertial Sensor. Sensors, 20(7), 2083. https://doi.org/10.3390/s20072083






