Prediction of I–V Characteristic Curve for Photovoltaic Modules Based on Convolutional Neural Network
Abstract
1. Introduction
2. Experimental Equipment and Data Acquisition
3. Models Building and Training
3.1. MLP Model Establishment
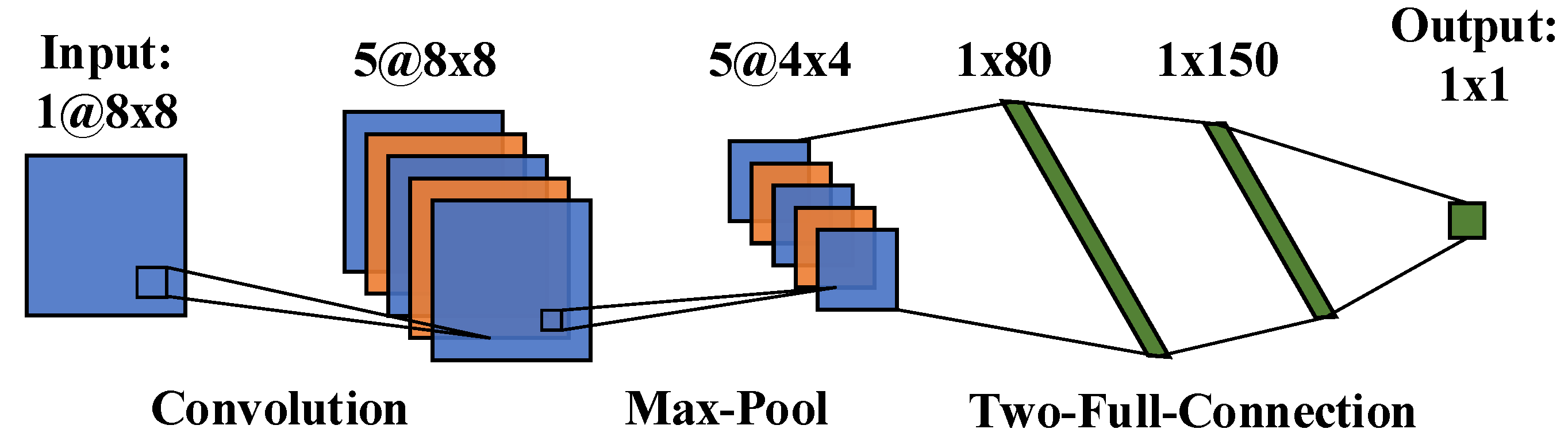
3.2. CNN Model Establishment
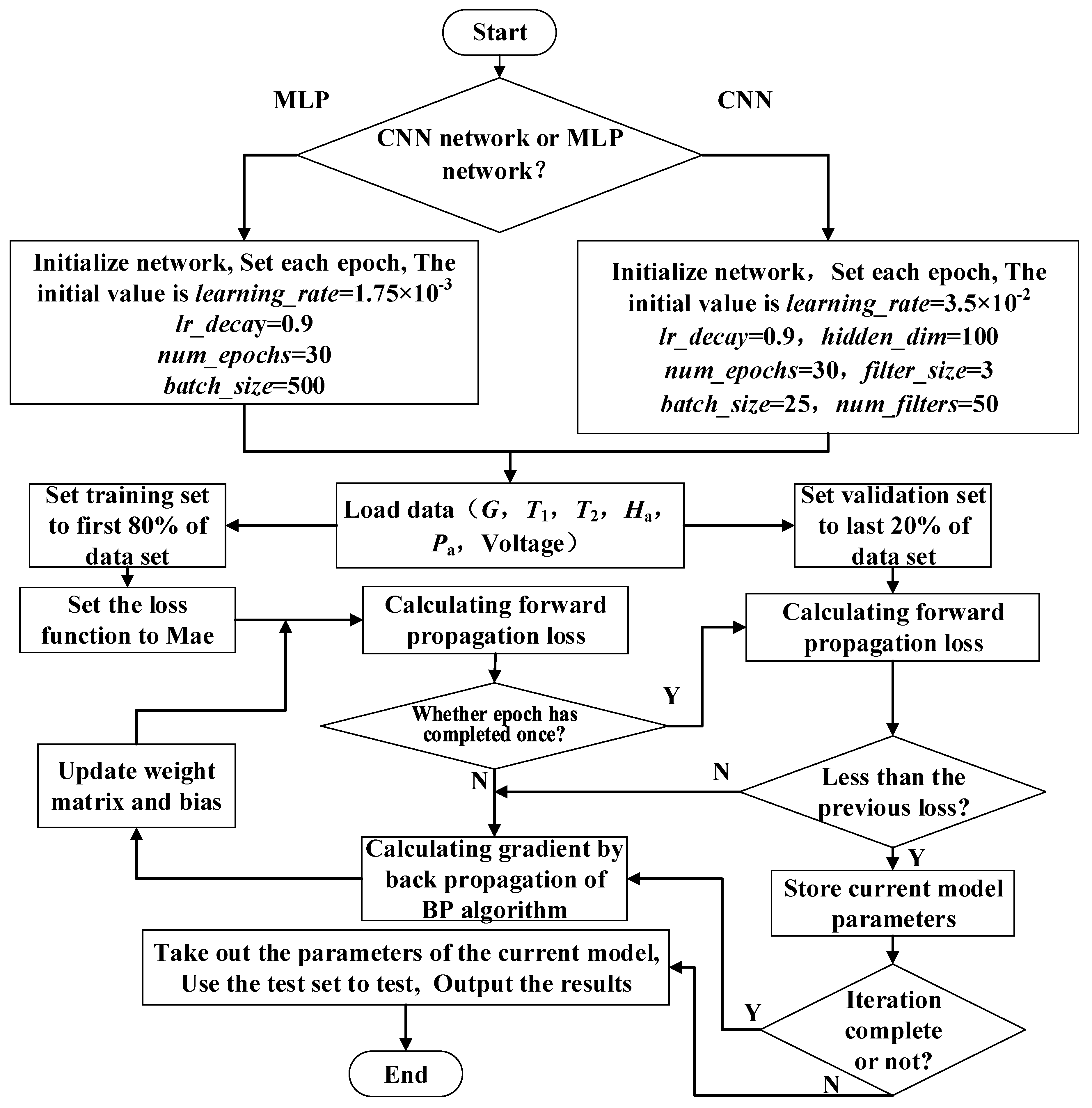
3.3. Model Training
4. Results Analysis
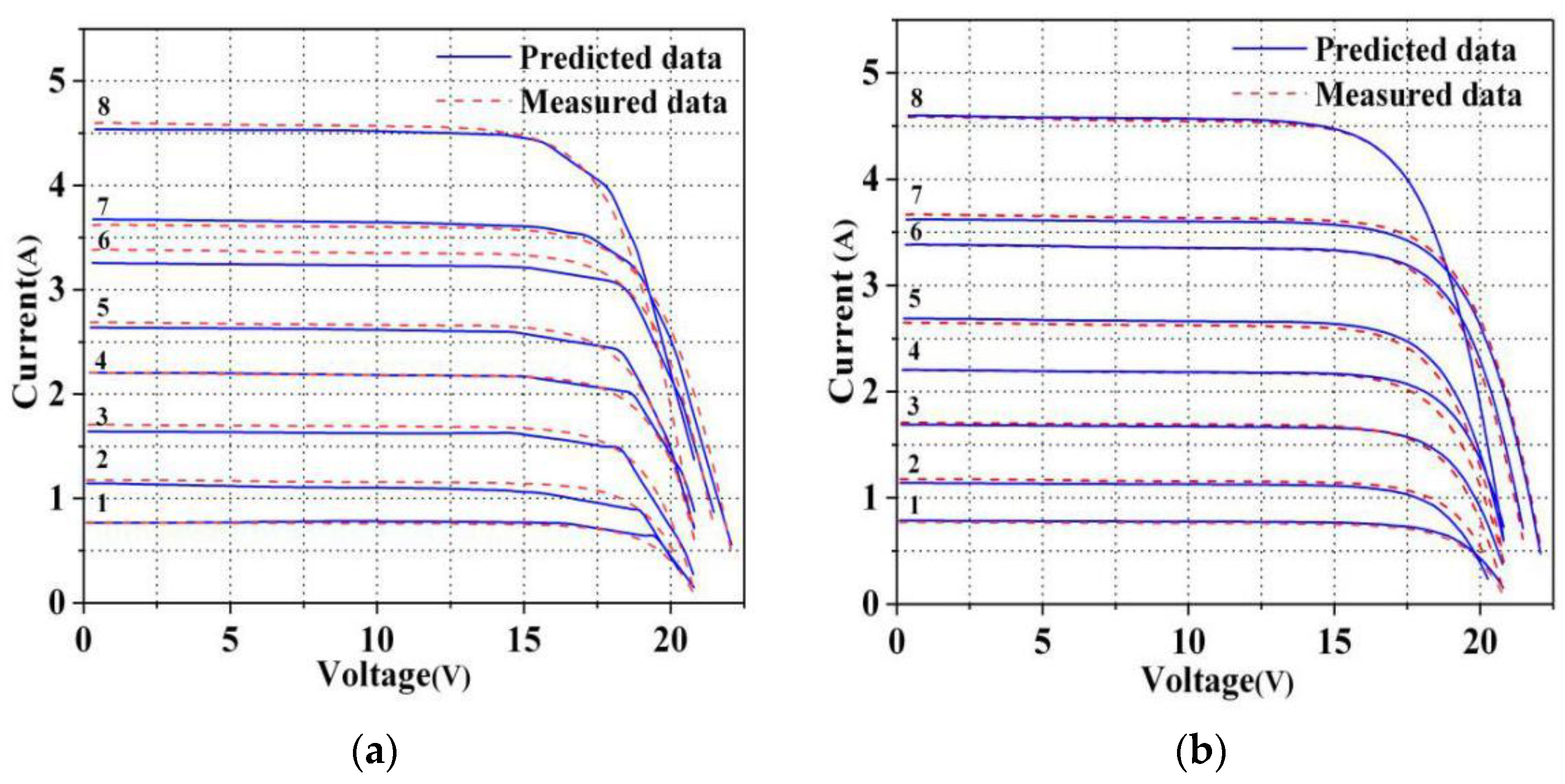
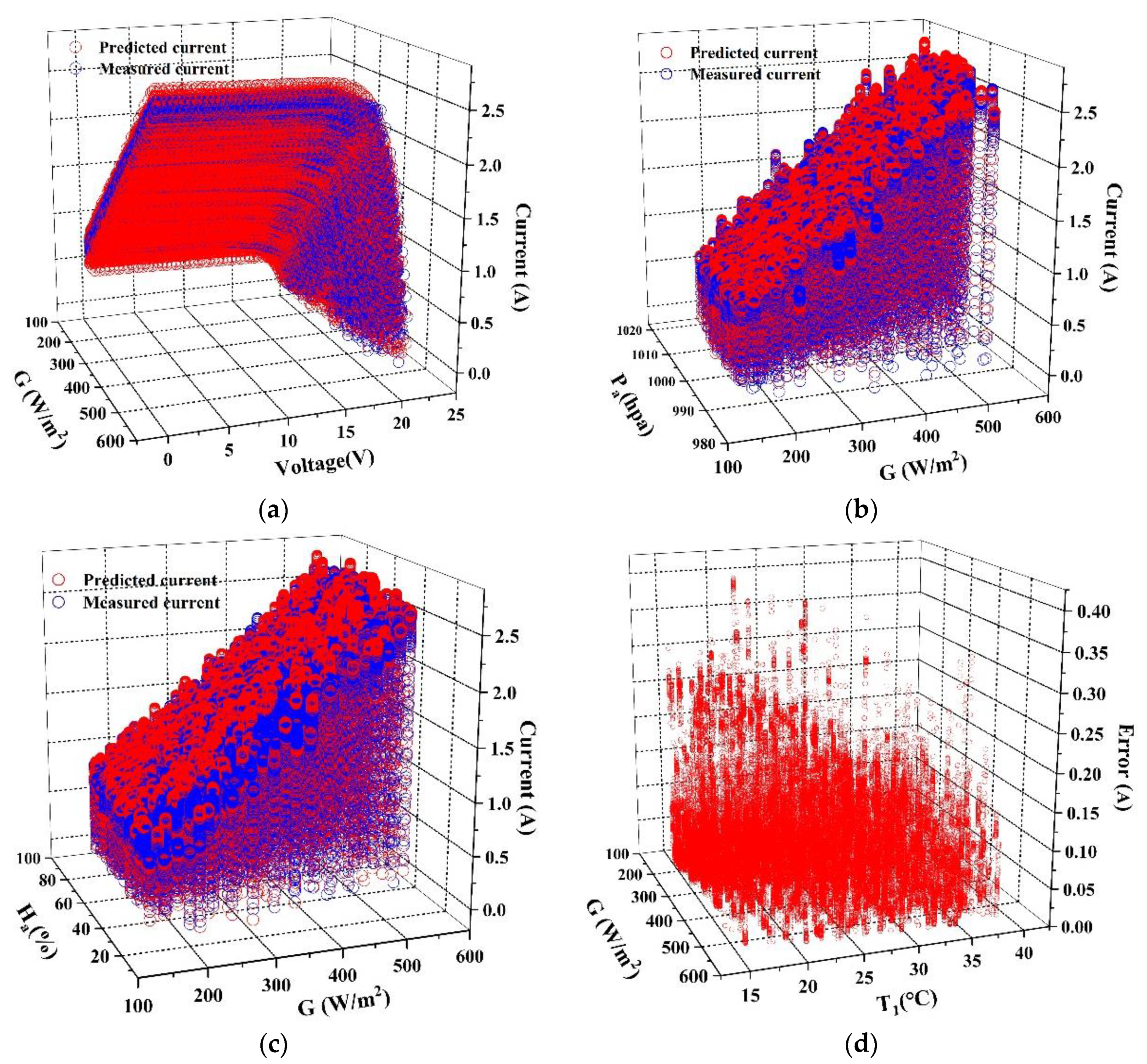
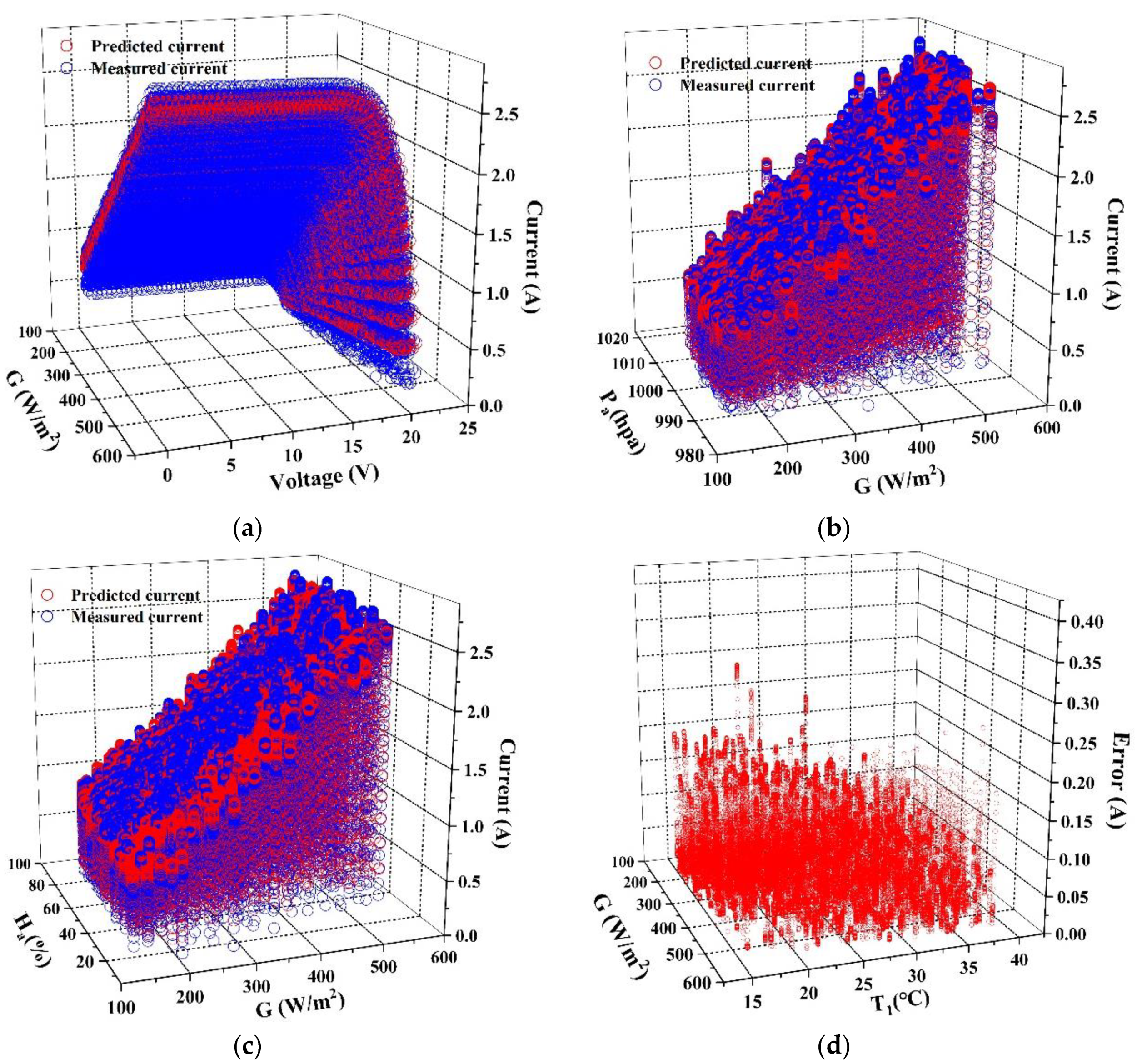
4.1. The Accuracy Analysis
4.2. Analysis of the Fitting Degree
4.3. Comparison with Equivalent Circuit Method
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- A Snapshot of Global Photovoltaic Markets 2019; IEA-PVPS: Paris, France, 2019.
- Chin, V.J.; Chin, V.J.; Ishaque, K. Cell modelling and model parameters estimation techniques for photovoltaic simulator application: A review. Appl. Energy 2015, 154, 500–519. [Google Scholar] [CrossRef]
- Almonacid, F.; Fernandez, E.F.; Mellit, A.; Kalogirou, S. Review of techniques based on artificial neural networks for the electrical characterization of concentrator photovoltaic technology. Renew. Sustain. Energy Rev. 2017, 75, 938–953. [Google Scholar] [CrossRef]
- Ram, J.P.; Manghani, H.; Pillai, D.S.; Babu, T.S.; Miyatake, M.; Rajasekar, N. Analysis on solar PV emulators: A review. Renew. Sustain. Energy Rev. 2018, 81, 149–160. [Google Scholar] [CrossRef]
- Ram, J.P.; Babu, T.S.; Rajasekar, N. A comprehensive review on solar PV maximum power point tracking techniques. Renew. Sustain. Energy Rev. 2017, 67, 826–847. [Google Scholar] [CrossRef]
- Chou, K.Y.; Yang, S.-T.; Chen, Y.-P. Maximum Power Point Tracking of Photovoltaic System Based on Reinforcement Learning. Sensors 2019, 19, 5054. [Google Scholar] [CrossRef]
- Lee, S.; Choi, D.-H. Reinforcement Learning-Based Energy Management of Smart Home with Rooftop Solar Photovoltaic System, Energy Storage System, and Home Appliances. Sensors 2019, 19, 3937. [Google Scholar] [CrossRef]
- Pozo, B.; Garate, J.I.; Araujo, J.Á.; Ferreiro, S. Photovoltaic Energy Harvesting System Adapted for Different Environmental Operation Conditions: Analysis, Modeling, Simulation and Selection of Devices. Sensors 2019, 19, 1578. [Google Scholar] [CrossRef]
- Antolín, D.; Medrano, N.; Calvo, B.; Martínez, P.A. A Compact Energy Harvesting System for Outdoor Wireless Sensor Nodes Based on a Low-Cost In Situ Photovoltaic Panel Characterization-Modelling Unit. Sensors 2017, 17, 1794. [Google Scholar] [CrossRef]
- Miñambres-Marcos, V.M.; Guerrero-Martínez, M.Á.; Barrero-Gonzalez, F.; GMilanes-Montero, M.I. A Grid Connected Photovoltaic Inverter with Battery-Supercapacitor Hybrid Energy Storage. Sensors 2017, 17, 1856. [Google Scholar] [CrossRef]
- Dhimish, M.; Holmes, V.; Mehrdadi, B.; Dales, M.; Mather, P. Photovoltaic fault detection algorithm based on theoretical curves modelling and fuzzy classification system. Energy 2017, 140, 276–290. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, L.; Cheng, S.; Lin, P.; Wu, Y.; Lin, W. Intelligent fault diagnosis of photovoltaic arrays based on optimized kernel extreme learning machine and I-V characteristics. Appl. Energy 2017, 204, 912–931. [Google Scholar] [CrossRef]
- Chen, Z.; Han, F.; Wu, L.; Yu, J.; Cheng, S.; Lin, P.; Chen, H. Random forest based intelligent fault diagnosis for PV arrays using array voltage and string currents. Energy Convers. Manag. 2018, 178, 250–264. [Google Scholar] [CrossRef]
- Wu, L.; Chen, Z.; Long, C.; Cheng, S.; Lin, P.; Chen, Y.; Chen, H. Parameter extraction of photovoltaic models from measured I-V characteristics curves using a hybrid trust-region reflective algorithm. Appl. Energy 2018, 232, 36–53. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Huang, Z.; Xie, S.; Gu, W.; Xiao-Yan, W.; Lin, Z.; Zhang, Z. Current Characteristics Estimation of Si PV Modules Based on Artificial Neural Network Modeling. Mater. 2019, 12, 3037. [Google Scholar] [CrossRef] [PubMed]
- Caamaño-Martín, E.; Pigueiras, E.L.; Zillies, R. Quality control of wide collections of PV modules: Lessons learned from the IES experience. Prog. Photovoltaics Res. Appl. 1999, 7, 137–149. [Google Scholar] [CrossRef]
- Chaibi, Y.; Allouhi, A.; Malvoni, M.; Salhi, M.; Saadani, R. Solar irradiance and temperature influence on the photovoltaic cell equivalent-circuit models. Sol. Energy 2019, 188, 1102–1110. [Google Scholar] [CrossRef]
- Cuce, E.; Cuce, P.M.; Karakas, I.H.; Bali, T. An accurate model for photovoltaic (PV) modules to determine electrical characteristics and thermodynamic performance parameters. Energy Convers. Manag. 2017, 146, 205–216. [Google Scholar] [CrossRef]
- Yahya-Khotbehsara, A.; Shahhoseini, A. A fast modeling of the double-diode model for PV modules using combined analytical and numerical approach. Sol. Energy 2018, 162, 403–409. [Google Scholar] [CrossRef]
- Zhu, H.; Lian, W.; Lu, L.; Kamunyu, P.; Yu, C.; Dai, S.; Hu, Y. Online Modelling and Calculation for Operating Temperature of Silicon-Based PV Modules Based on BP-ANN. Int. J. Photoenergy 2017, 2017, 1–13. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, Y.; Wu, L.; Cheng, S.; Lin, P.; You, L. Accurate modeling of photovoltaic modules using a 1-D deep residual network based on I-V characteristics. Energy Convers. Manag. 2019, 186, 168–187. [Google Scholar] [CrossRef]
- Pillai, D.S.; Rajasekar, N. Metaheuristic algorithms for PV parameter identification: A comprehensive review with an application to threshold setting for fault detection in PV systems. Renew. Sustain. Energy Rev. 2018, 82, 3503–3525. [Google Scholar] [CrossRef]
- Jordehi, A.R. Parameter estimation of solar photovoltaic (PV) cells: A review. Renew. Sustain. Energy Rev. 2016, 61, 354–371. [Google Scholar] [CrossRef]
- Orioli, A.; Di Gangi, A. A procedure to calculate the five-parameter model of crystalline silicon photovoltaic modules on the basis of the tabular performance data. Appl. Energy 2013, 102, 1160–1177. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Shi, D.; He, Y. Parameter extraction of solar photovoltaic models using an improved whale optimization algorithm. Energy Convers. Manag. 2018, 174, 388–405. [Google Scholar] [CrossRef]
- Castro, R. Data-driven PV modules modelling: Comparison between equivalent electric circuit and artificial intelligence based models. Sustain. Energy Technol. Assessments 2018, 30, 230–238. [Google Scholar] [CrossRef]
- Tamer, K.; Ahmed, G.; Maan, T.; Mahmoud, J.; Saif, J. A new offline method for extracting I–V characteristic curve for photovoltaic modules using artificial neural networks. Solar Energy 2018, 173, 462–469. [Google Scholar]
- Piliougine, M.; Elizondo, D.; Mora-López, L.; Sidrach-De-Cardona, M. Photovoltaic module simulation by neural networks using solar spectral distribution. Prog. Photovoltaics: Res. Appl. 2012, 21, 1222–1235. [Google Scholar] [CrossRef]
- Piliougine, M.; Elizondo, D.; Mora-López, L.; Sidrach-De-Cardona, M. Multilayer perceptron applied to the estimation of the influence of the solar spectral distribution on thin-film photovoltaic modules. Appl. Energy 2013, 112, 610–617. [Google Scholar] [CrossRef]
- Singh, G.; Sachan, M.K. Multi-layer perceptron (MLP) neural network technique for offline handwritten Gurmukhi character recognition. In Proceedings of the 2014 IEEE International Conference on Computational Intelligence and Computing Research, Coimbatore, India, 18–20 December 2014; pp. 1–5. [Google Scholar]
- Kingma, D.P.; Ba, L.J. Adam: A method for stochastic optimization. arXiv 2004, arXiv:1412.6980. [Google Scholar]
- Lawrence, S.; Giles, C.; Tsoi, A.C.; Back, A. Face recognition: A convolutional neural-network approach. IEEE Trans. Neural Netw. 1997, 8, 98–113. [Google Scholar] [CrossRef]
- Sabry, Y.H.; Hasan, W.Z.W.; Sabry, A.H.; Ab Kadir, M.Z.A.; Radzi, M.A.M.; Shafie, S.; Sabri, Y.H.; Kader, M.Z.A. Measurement-Based Modeling of a Semitransparent CdTe Thin-Film PV Module Based on a Custom Neural Network. IEEE Access 2018, 6, 34934–34947. [Google Scholar] [CrossRef]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J.; Malik, J. Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 580–587. [Google Scholar]
- Hinton, G.; Mohamed, A.-R.; Jaitly, N.; Vanhoucke, V.; Kingsbury, B.; Deng, L.; Yu, D.; Dahl, G.; Senior, A.W.; Nguyen, P.; et al. Deep Neural Networks for Acoustic Modeling in Speech Recognition: The Shared Views of Four Research Groups. IEEE Signal Process. Mag. 2012, 29, 82–97. [Google Scholar] [CrossRef]
- Trier, Ø.D.; Jain, A.K.; Taxt, T. Feature extraction methods for character recognition-A survey. Pattern Recognit. 1996, 29, 641–662. [Google Scholar] [CrossRef]
- Celik, A.N.; Acikgoz, N. Modelling and experimental verification of the operating current of mono-crystalline photovoltaic modules using four- and five-parameter models. Appl. Energy 2007, 84, 1–15. [Google Scholar] [CrossRef]
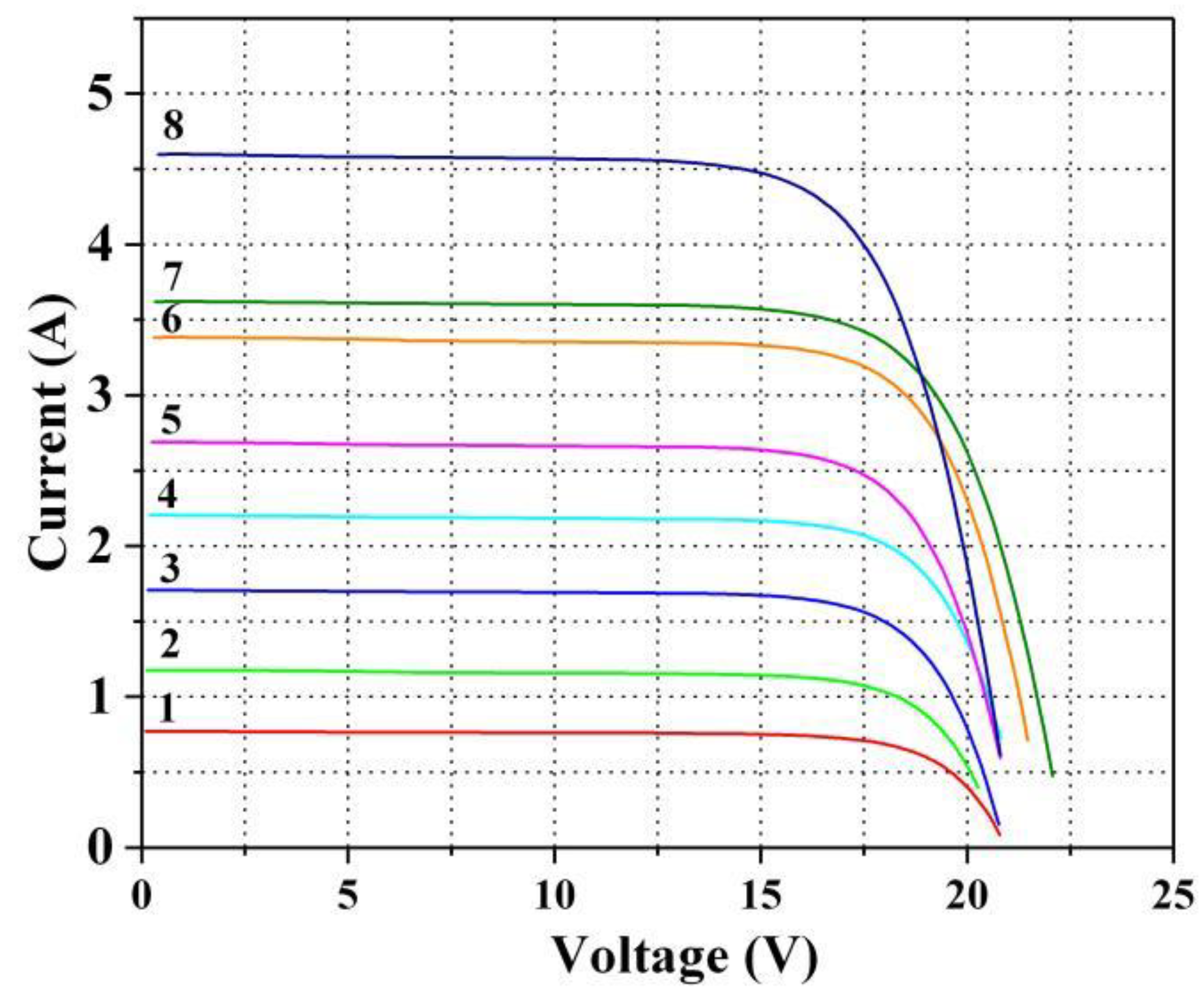


| Working Conditions | Irradiance G (W/m2) | Temperature of PV Module Back-Surface T1 (°C) | Ambient Temperature T2 (°C) | Relative Humidity Ha (%) | Atmospheric Pressure Pa (hPa) |
|---|---|---|---|---|---|
| 1 | 153.7 | 16.8 | 21.9 | 83.2 | 1002.9 |
| 2 | 237.5 | 23.3 | 24.6 | 42.3 | 1001.4 |
| 3 | 328.7 | 26.9 | 24.7 | 69.7 | 997.1 |
| 4 | 445.5 | 22.7 | 24.8 | 58.4 | 1007.6 |
| 5 | 537.9 | 28.2 | 24.3 | 59.0 | 1006.5 |
| 6 | 653.4 | 22.8 | 22.1 | 88.3 | 1007.9 |
| 7 | 726.9 | 19.5 | 23.4 | 73.8 | 1001.8 |
| 8 | 909.0 | 36.2 | 25.7 | 71.1 | 1015.1 |
| Working Conditions | Irradiance G (W/m2) | Algorithms | MAE (%) | RMSE (%) |
|---|---|---|---|---|
| 1 | 153.7 | MLP | 2.0 | 3.0 |
| CNN | 1.9 | 2.1 | ||
| 2 | 237.5 | MLP | 6.0 | 6.6 |
| CNN | 1.8 | 3.9 | ||
| 3 | 328.7 | MLP | 6.7 | 7.0 |
| CNN | 3.3 | 4.8 | ||
| 4 | 445.5 | MLP | 2.2 | 4.5 |
| CNN | 1.5 | 3.3 | ||
| 5 | 537.9 | MLP | 5.0 | 5.3 |
| CNN | 2.1 | 3.4 | ||
| 6 | 653.4 | MLP | 11.0 | 11.7 |
| CNN | 2.6 | 4.7 | ||
| 7 | 726.9 | MLP | 6.0 | 8.0 |
| CNN | 1.5 | 2.1 | ||
| 8 | 909.0 | MLP | 11.5 | 19.2 |
| CNN | 1.4 | 1.5 |
| Working Conditions | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Irradiance G (W/m2) | 153.7 | 328.7 | 537.9 | 726.9 |
| MAE | 0.443 | 0.975 | 1.236 | 0.998 |
| RMSE | 0.335 | 0.766 | 0.895 | 0.864 |
| Evaluation Method | Equivalent Circuit Method | CNN Model | MLP Model |
|---|---|---|---|
| MAE | 0.864 | 0.0307 | 0.0671 |
| RMSE | 0.445 | 0.0322 | 0.0816 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Li, R.; Jia, Y.; Zhang, Z. Prediction of I–V Characteristic Curve for Photovoltaic Modules Based on Convolutional Neural Network. Sensors 2020, 20, 2119. https://doi.org/10.3390/s20072119
Li J, Li R, Jia Y, Zhang Z. Prediction of I–V Characteristic Curve for Photovoltaic Modules Based on Convolutional Neural Network. Sensors. 2020; 20(7):2119. https://doi.org/10.3390/s20072119
Chicago/Turabian StyleLi, Jie, Runran Li, Yuanjie Jia, and Zhixin Zhang. 2020. "Prediction of I–V Characteristic Curve for Photovoltaic Modules Based on Convolutional Neural Network" Sensors 20, no. 7: 2119. https://doi.org/10.3390/s20072119
APA StyleLi, J., Li, R., Jia, Y., & Zhang, Z. (2020). Prediction of I–V Characteristic Curve for Photovoltaic Modules Based on Convolutional Neural Network. Sensors, 20(7), 2119. https://doi.org/10.3390/s20072119





