Inlet Effect Caused by Multichannel Structure for Molecular Electronic Transducer Based on a Turbulent-Laminar Flow Model
Abstract
:1. Introduction
2. Mathematical Modeling
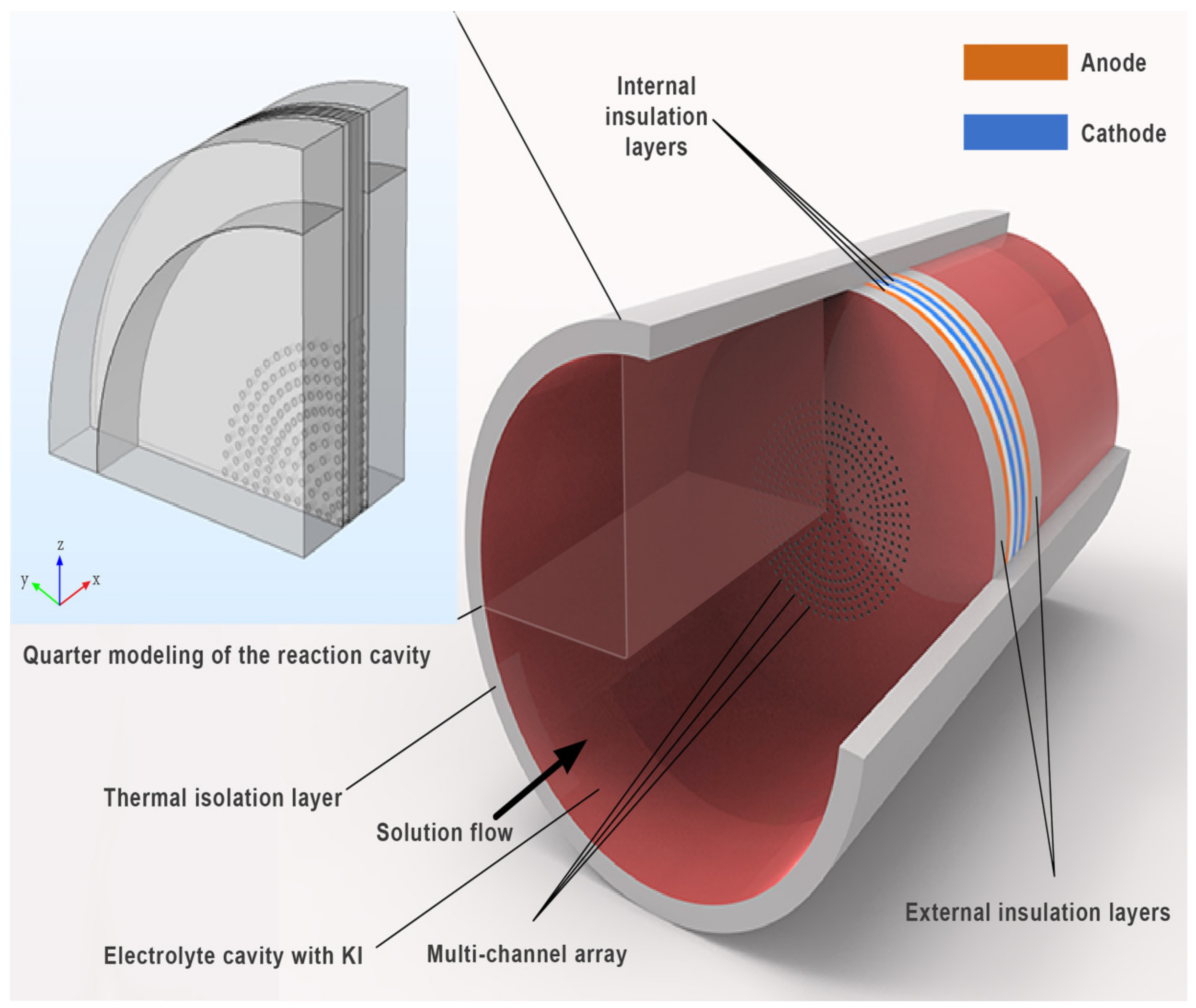
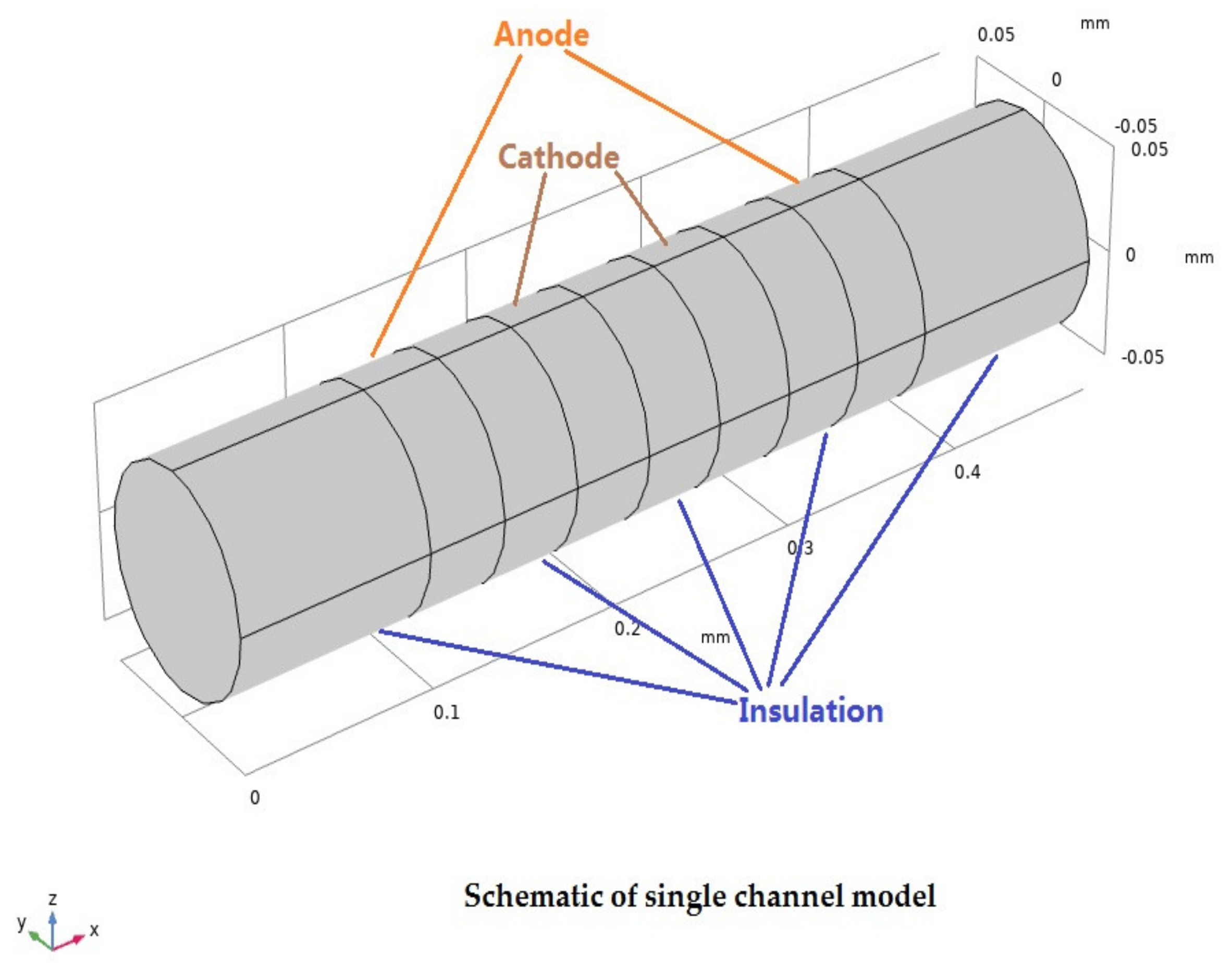
2.1. Geometry Model
2.2. Numerical Model
2.3. Boundary Conditions and Parameter Settings
3. Simulation and Discussion
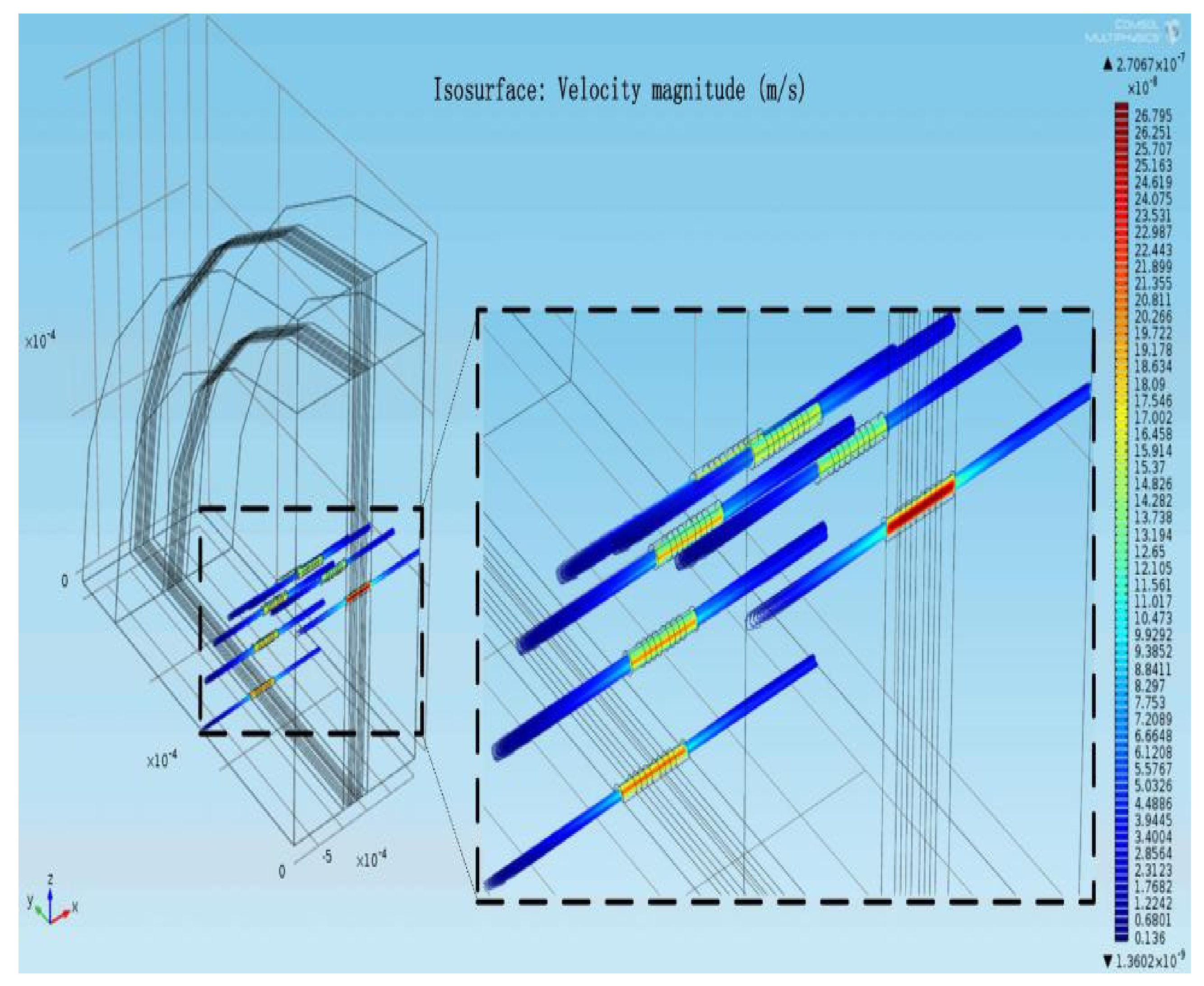
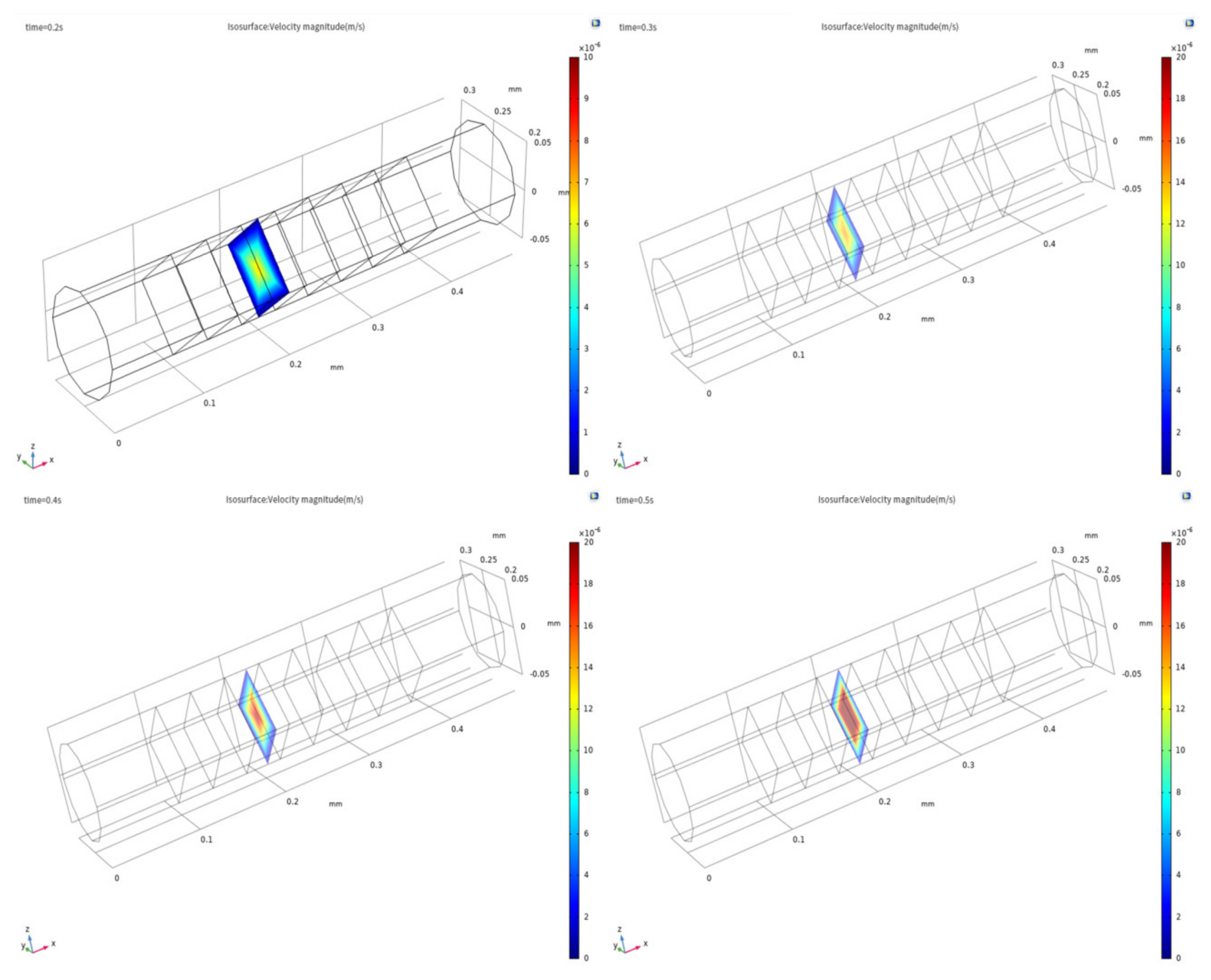
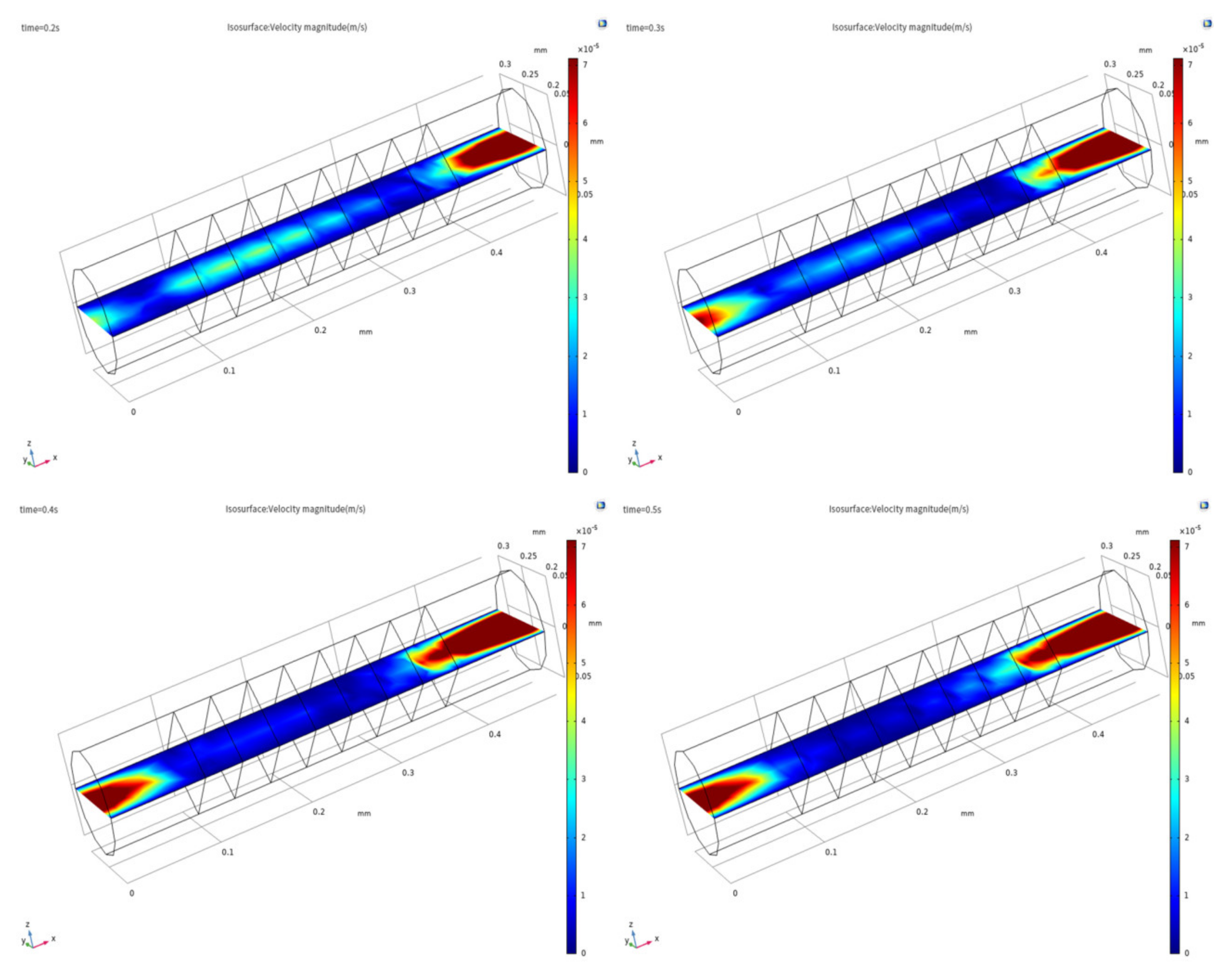
3.1. Evidence of Turbulence - Laminar Flow Phenomena and Multichannel Inlet/outlet Effects
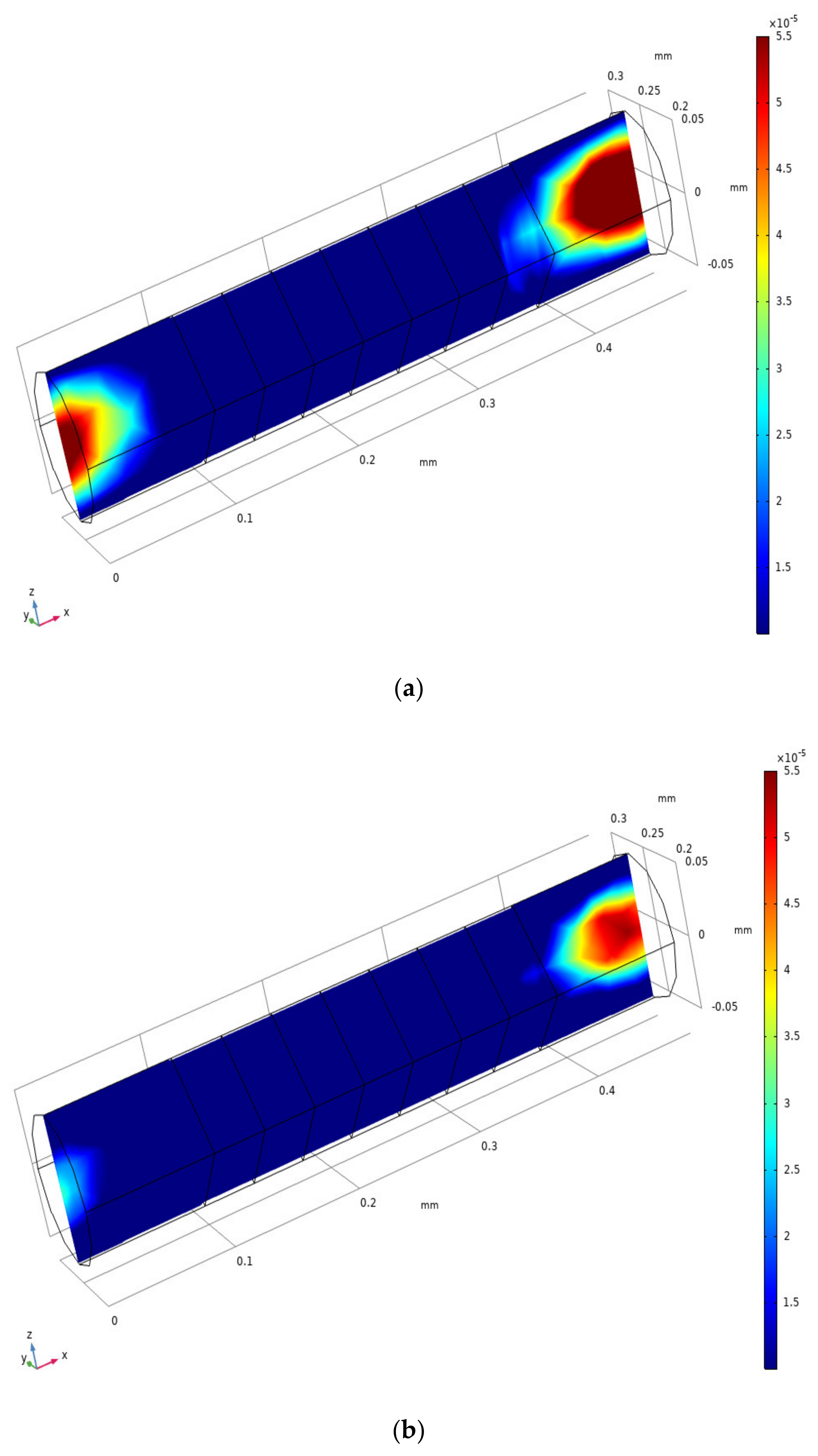
3.2. Analysis of the Inlet/outlet Effect
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Huang, H.; Liang, M.; Tang, R.; Oiler, J.; Yu, H. Molecular Electronic Transducer-Based Low-Frequency Accelerometer Fabricated with Post-CMOS Compatible Process Using Droplet as Sensing Body. IEEE Electron Device Lett. 2013, 34, 1304–1306. [Google Scholar] [CrossRef]
- Krishtop, V.G.; Bugaev, A.S.; Agafonov, V.M. Technological principles of motion parameter transducers based on mass and charge transport in electrochemical microsystems. J. Electrochem. 2012, 48, 746–755. [Google Scholar] [CrossRef]
- Zaitsev, D.L.; Avdyukhina, S.Y.; Ryzhkov, M.A. Frequency response and self-noise of the MET hydrophone. J. Sens. Sens. Syst. 2018, 7, 443–452. [Google Scholar] [CrossRef] [Green Version]
- Dmitry, Z.; Vadim, A.; Egor, E.; Alexander, A.; Anna, S. Molecular Electronic Angular Motion Transducer Broad Band Self-Noise. Sensors 2015, 15, 29378–29392. [Google Scholar]
- Zhou, Q.; Wang, C.; Chen, Y.; Chen, S.; Lin, J. Dynamic Response Analysis of Microflow Electrochemical Sensors with Two Types of Elastic Membrane. Sensors 2016, 16, 657. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Agafonov, V.M. Modeling the Convective Noise in an Electrochemical Motion Transducer. Int. J. Electrochem. Sci. 2018, 13, 11432–11442. [Google Scholar]
- Egorov, I.V.; Shabalina, A.S.; Agafonov, V.M. Design and Self-Noise of MET Closed-Loop Seismic Accelerometers. IEEE Sens. J. 2017, 17, 2008–2014. [Google Scholar] [CrossRef]
- Sun, Z.; Agafonov, V.M. 3D numerical simulation of the pressure-driven flow in a four-electrode rectangular micro-electrochemical accelerometer. Sens. Actuator B Chem. 2010, 146, 231–238. [Google Scholar] [CrossRef]
- Huang, H.; Carande, B.; Tang, R.; Oiler, J.; Zaitsev, D.; Agafonov, V.; Yu, H. Development of a micro seismometer based on molecular electronic transducer technology for planetary exploration. In Proceedings of the IEEE 26th International Conference on Micro Electro Mechanical Systems, MEMS 2013, Taipei, Taiwan, 20–24 January 2013; pp. 629–632. [Google Scholar]
- Li, Z.; Zhang, H.; Liu, Y.; McDonough, J.M. Implementation of compressible porous-fluid coupling method in an aerodynamics and aeroacoustics code part I: Laminar flow. Appl. Math. Comput. 2020, 364, 124682. [Google Scholar] [CrossRef]
- Wang, Y.; Zhong, C.; Cao, J.; Zhuo, C.; Liu, S. A simplified finite volume lattice Boltzmann method for simulations of fluid flows from laminar to turbulent regime, Part II: Extension towards turbulent flow simulation. Comput. Math. Appl. 2019, in press. [Google Scholar] [CrossRef] [Green Version]
- Dickinson, E.J.F.; Ekström, H.; Fontes, E. COMSOL Multiphysics®: Finite element software for electrochemical analysis. A mini-review. Electrochem. Commun. 2014, 40, 71–74. [Google Scholar] [CrossRef]
- Volgin, V.M.; Davydov, A.D. Mass-transfer problems in the electrochemical systems. Russ. J. Electrochem. 2012, 48, 565–569. [Google Scholar] [CrossRef]
- Agafonov, V.; Egorov, E. Electrochemical accelerometer with DC response, experimental and theoretical study. J. Electroanal. Chem. 2016, 761, 8–13. [Google Scholar] [CrossRef]
- Sun, Z.; Agafonov, V.M. Computational study of the pressure-driven flow in a four-electrode rectangular micro-electrochemical accelerometer with an infinite aspect ratio. Electrochim. Acta 2010, 55, 2036–2043. [Google Scholar] [CrossRef]


| Characteristic Parameters | Symbol | Value |
|---|---|---|
| Electrolyte temperature | ||
| Ion mobility | ||
| Electrode reaction constant | ||
| Equilibrium potential | ||
| The density of water | ||
| Viscosity of water | ||
| The density of electrolyte | ||
| Viscosity of electrolyte | ||
| Electrolyte temperature | 300 K | |
| Ion mobility |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; He, Q.; Chen, Y.; Bao, X. Inlet Effect Caused by Multichannel Structure for Molecular Electronic Transducer Based on a Turbulent-Laminar Flow Model. Sensors 2020, 20, 2154. https://doi.org/10.3390/s20072154
Zhou Q, He Q, Chen Y, Bao X. Inlet Effect Caused by Multichannel Structure for Molecular Electronic Transducer Based on a Turbulent-Laminar Flow Model. Sensors. 2020; 20(7):2154. https://doi.org/10.3390/s20072154
Chicago/Turabian StyleZhou, Qiuzhan, Qi He, Yuzhu Chen, and Xue Bao. 2020. "Inlet Effect Caused by Multichannel Structure for Molecular Electronic Transducer Based on a Turbulent-Laminar Flow Model" Sensors 20, no. 7: 2154. https://doi.org/10.3390/s20072154
APA StyleZhou, Q., He, Q., Chen, Y., & Bao, X. (2020). Inlet Effect Caused by Multichannel Structure for Molecular Electronic Transducer Based on a Turbulent-Laminar Flow Model. Sensors, 20(7), 2154. https://doi.org/10.3390/s20072154





