Coherent Integration Method Based on Radon-NUFFT for Moving Target Detection Using Frequency Agile Radar
Abstract
:1. Introduction
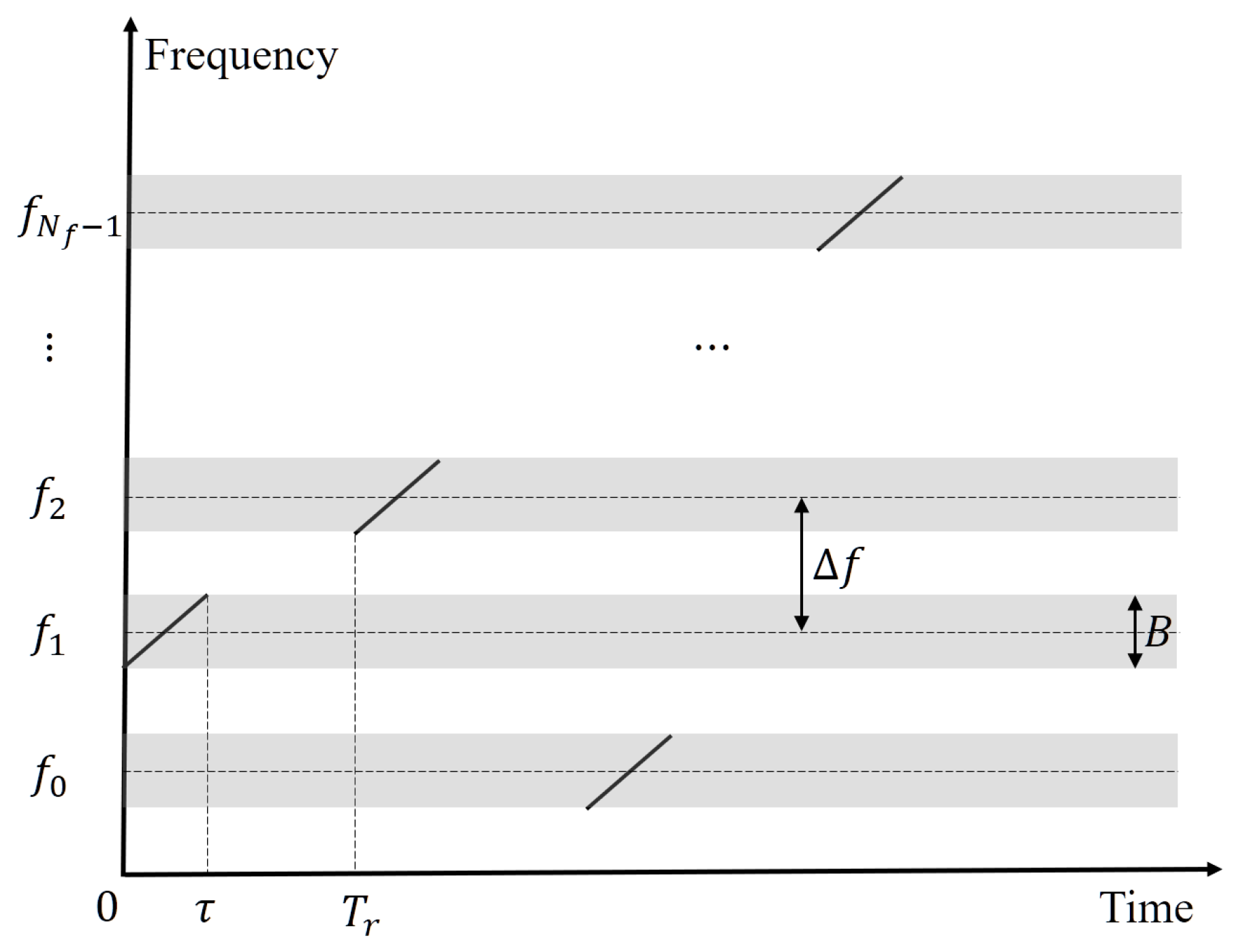
2. Signal Model
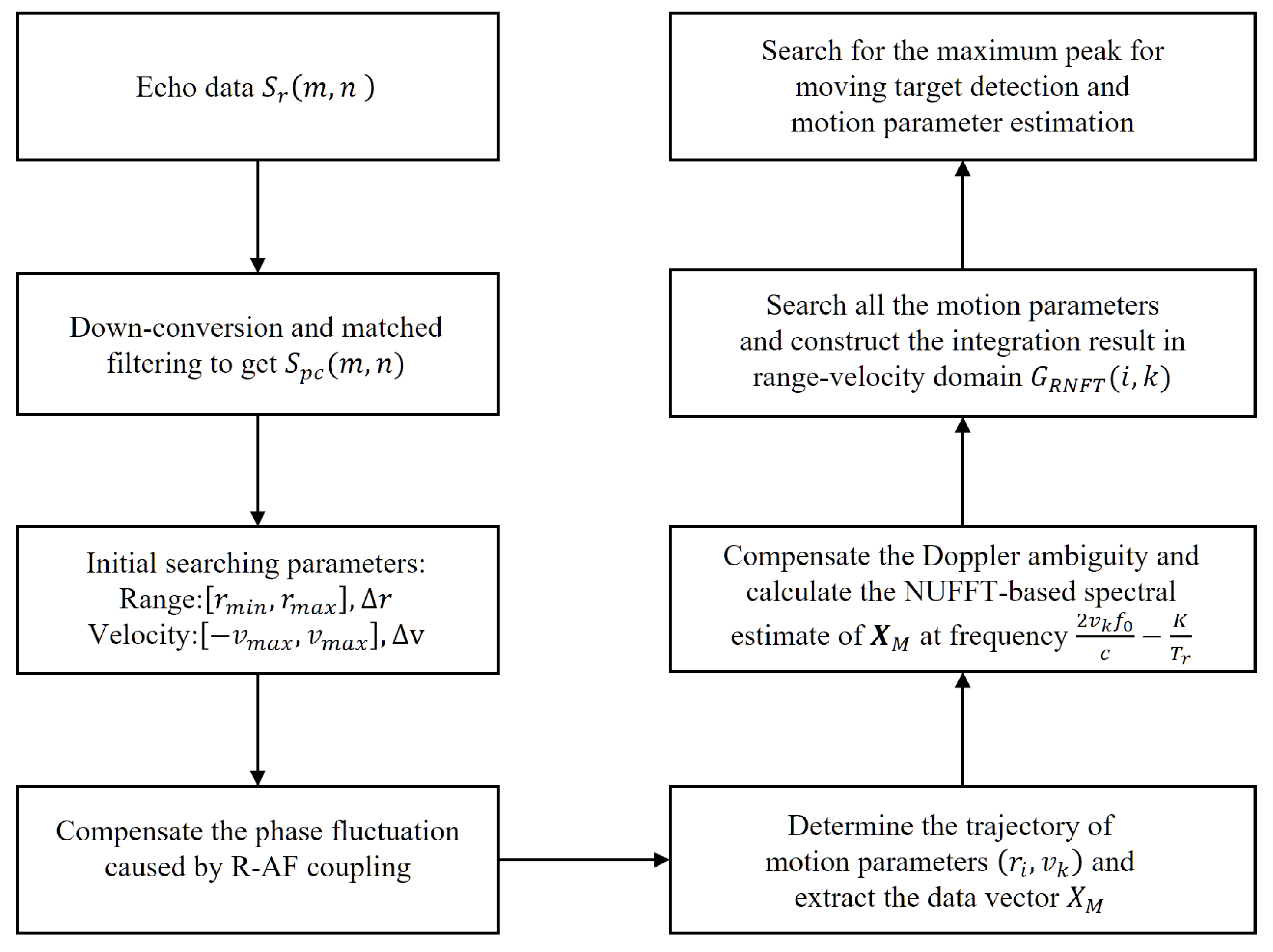
3. Proposed Method
3.1. NUFFT Based on Low Rank Approximation
3.2. Radon-NUFFT Method
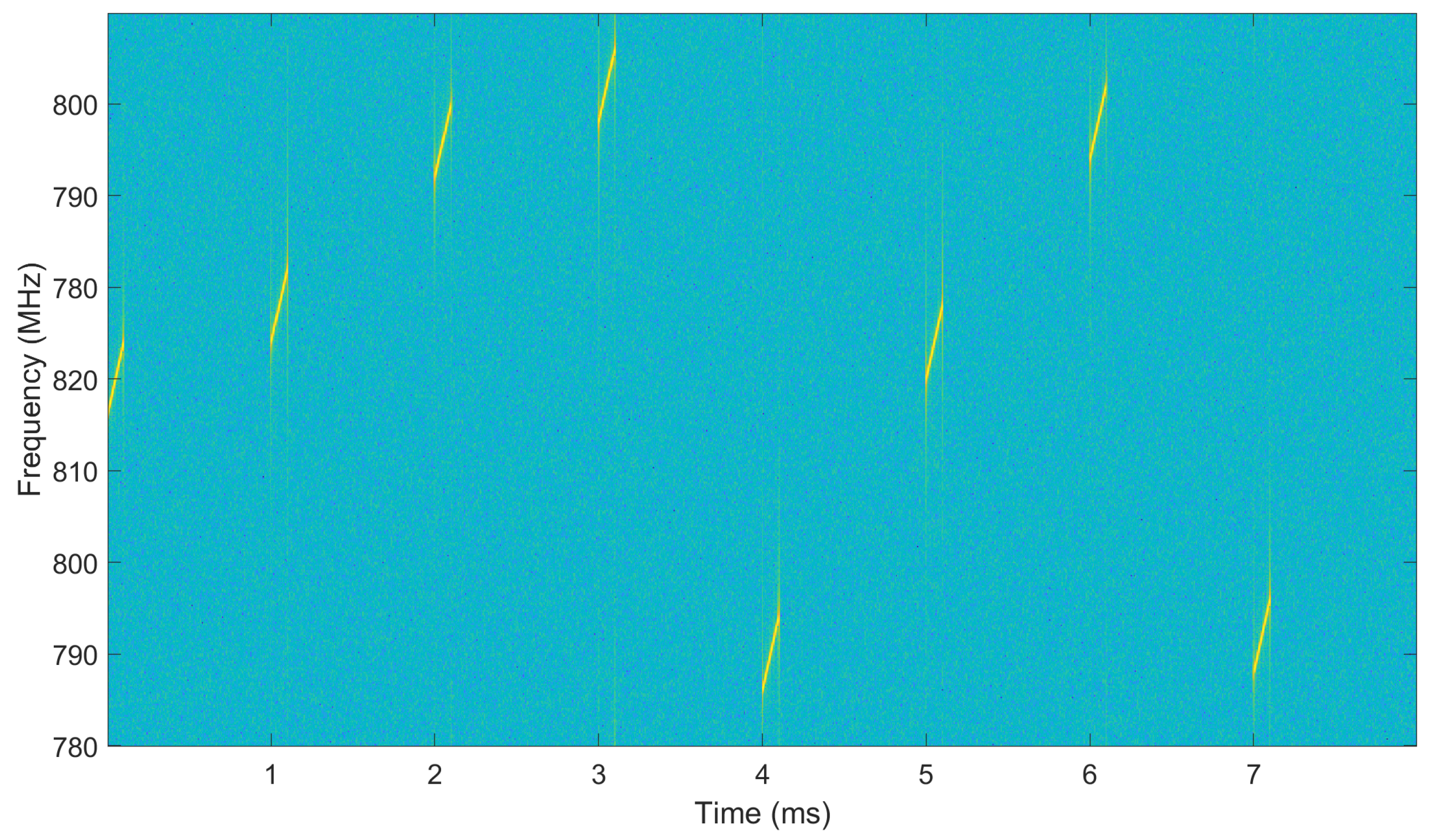
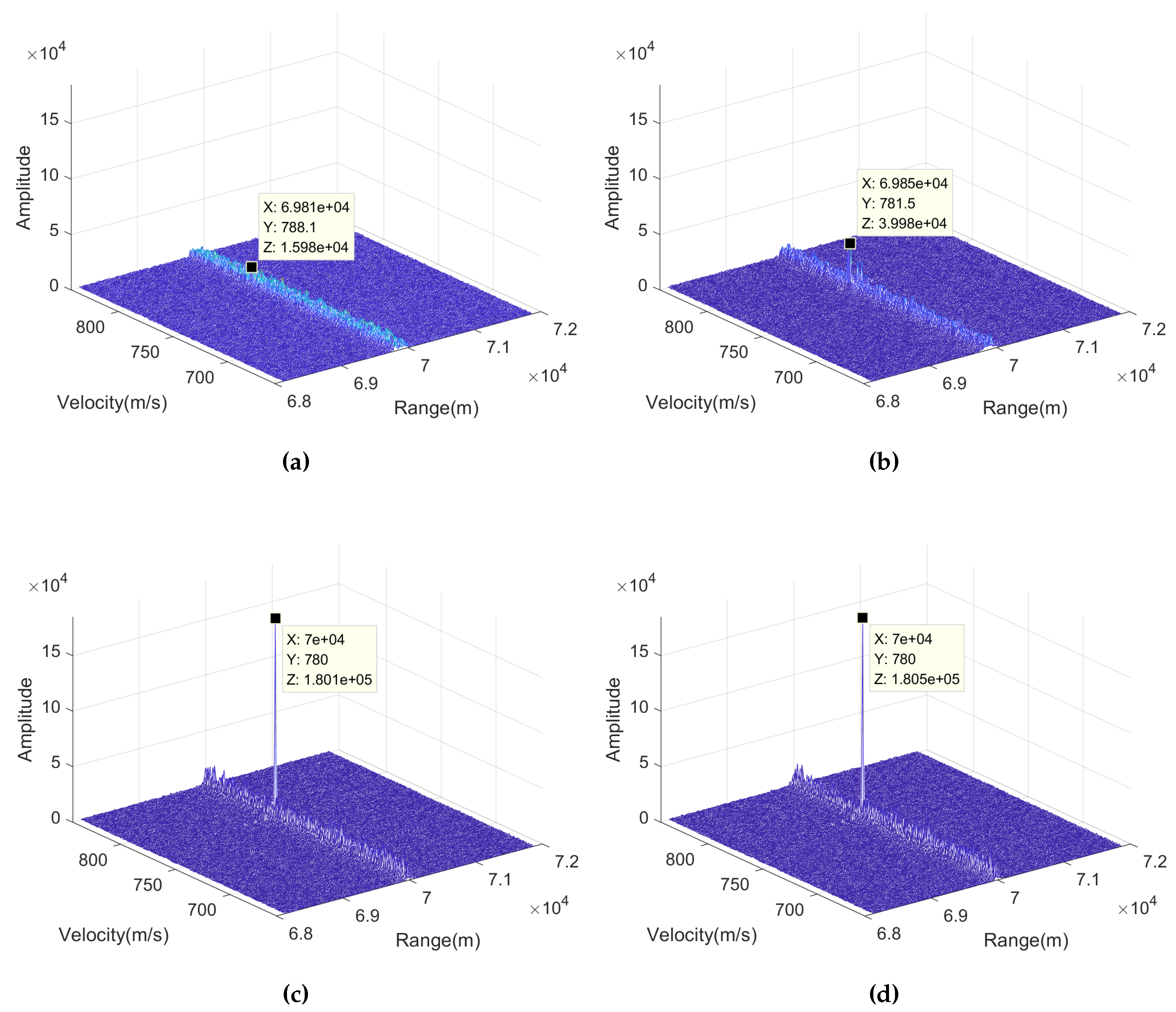
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ahmed, S. Novel noncoherent radar pulse integration to combat noise jamming. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2350–2359. [Google Scholar] [CrossRef]
- Liu, Y.; Meng, H.; Li, G.; Wang, X. Range-velocity estimation of multiple targets in randomised stepped-frequency radar. Electron. Lett. 2008, 44, 1032–1034. [Google Scholar] [CrossRef]
- Shan, T.; Liu, S.; Zhang, Y.D.; Amin, M.G.; Tao, R.; Feng, Y. Efficient architecture and hardware implementation of coherent integration processor for digital video broadcast-based passive bistatic radar. IET Radar, Sonar Navigation 2016, 10, 97–106. [Google Scholar] [CrossRef]
- Xu, J.; Yu, J.; Peng, Y.N.; Xia, X.G. Radon-Fourier Transform for Radar Target Detection, I: Generalized Doppler Filter Bank. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 1186–1202. [Google Scholar] [CrossRef]
- Liu, S.; Shan, T.; Tao, R.; Zhang, Y.D.; Zhang, G.; Zhang, F.; Wang, Y. Sparse Discrete Fractional Fourier Transform and Its Applications. IEEE Trans. Signal Process. 2014, 62, 6582–6595. [Google Scholar] [CrossRef] [Green Version]
- Pang, C.; Liu, S.; Han, Y. Coherent Detection Algorithm for Radar Maneuvering Targets Based on Discrete Polynomial-Phase Transform. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2019, 12, 1–11. [Google Scholar] [CrossRef]
- Li, X.; Cui, G.; Yi, W.; Kong, L. Coherent Integration for Maneuvering Target Detection Based on Radon-Lv’s Distribution. IEEE Signal Process. Lett. 2015, 22, 1467–1471. [Google Scholar] [CrossRef]
- Suksmono, A.B.; Bharata, E.; Lestari, A.A.; Yarovoy, A.G.; Ligthart, L.P. Compressive Stepped-Frequency Continuous-Wave Ground-Penetrating Radar. IEEE Geosci. Remote Sens. Lett. 2010, 7, 665–669. [Google Scholar] [CrossRef]
- Huang, T.; Liu, Y.; Meng, H.; Wang, X. Cognitive random stepped frequency radar with sparse recovery. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 858–870. [Google Scholar] [CrossRef]
- Zhou, R.; Xia, G.; Zhao, Y.; Liu, H. Coherent signal processing method for frequency-agile radar. In Proceedings of the 2015 12th IEEE International Conference on Electronic Measurement Instruments (ICEMI), Qingdao, China, 16–18 July 2015; Volume 1, pp. 431–434. [Google Scholar] [CrossRef]
- Wang, D.; Lin, C.; Bao, Q.; Chen, Z. Long-time coherent integration method for high-speed target detection using frequency agile radar. Electron. Lett. 2016, 52, 960–962. [Google Scholar] [CrossRef]
- VanderPlas, J. Understanding the Lomb-Scargle Periodogram. Astrophys. J. Suppl. Ser. 2017, 236. [Google Scholar] [CrossRef]
- Stoica, P.; Li, J.; He, H. Spectral Analysis of Nonuniformly Sampled Data: A New Approach Versus the Periodogram. IEEE Trans. Signal Process. 2009, 57, 843–858. [Google Scholar] [CrossRef]
- Bagchi, S.; Mitra, S. The Nonuniform Discrete Fourier Transform and Its Applications in Signal Processing; Springer: New York, NY, USA, 1999. [Google Scholar] [CrossRef]
- Dutt, A.; Rokhlin, V. Fast Fourier Transforms for Nonequispaced Data. SIAM J. Sci. Comput 1993, 14, 1368–1393. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.H.; Nguyen, N. An accurate algorithm for nonuniform fast Fourier transforms (NUFFT’s). IEEE Microw. Guided Wave Lett. 1998, 8, 18–20. [Google Scholar] [CrossRef]
- Greengard, L.; Lee, J.Y. Accelerating the Nonuniform Fast Fourier Transform. SIAM Rev. 2004, 46, 443–454. [Google Scholar] [CrossRef] [Green Version]
- Fessler, J.A.; Sutton, B.P. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans. Signal Process. 2003, 51, 560–574. [Google Scholar] [CrossRef] [Green Version]
- Ruiz-Antolín, D.; Townsend, A. A Nonuniform Fast Fourier Transform Based on Low Rank Approximation. SIAM J. Sci. Comput. 2017, 40. [Google Scholar] [CrossRef] [Green Version]
- Cooley, J.; Tukey, J. An Algorithm for the Machine Calculation of Complex Fourier Series. Math. Comput. 1965, 19, 297–301. [Google Scholar] [CrossRef]
- Kunis, S.; Melzer, I. Fast evaluation of real and complex exponential sums. Electron. Trans. Numer. Anal. 2017, 46, 23–35. [Google Scholar]
- Townsend, A.; Webb, M.; Olver, S. Fast polynomial transforms based on Toeplitz and Hankel matrices. Math. Comput. 2018, 87, 1913–1934. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions, 1st ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Parl, S. A new method of calculating the generalized Q function (Corresp.). IEEE Trans. Inf. Theory 1980, 26, 121–124. [Google Scholar] [CrossRef]


| Simulated Parameters (Unit) | Values |
|---|---|
| Average carrier frequency (MHz) | 800 |
| Variation range of carrier frequency (MHz) | [780,820] |
| Variation interval of carrier frequency (MHz) | 1 |
| Sampling frequency (MHz) | 8 |
| Bandwidth (MHz) | 4 |
| Pulse width (us) | 100 |
| Pulse repetition interval(us) | 1000 |
| Number of coherently integrated pulses | 256 |
| Initial distance of target (km) | 70 |
| Radial velocity of target (m/s) | 780 |
| Method | Range (m) | Velocity (m/s) | Amplitude |
|---|---|---|---|
| MTD | |||
| NUFFT | |||
| FA-CRT | 780 | ||
| Radon-NUFFT | 780 |
| Method | MTD | NUFFT | Radon-NUFFT | FA-CRT |
|---|---|---|---|---|
| Computing time(s) | 0.003796 | 0.036970 | 0.684318 | 6.105591 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pan, J.; Zhu, Q.; Bao, Q.; Chen, Z. Coherent Integration Method Based on Radon-NUFFT for Moving Target Detection Using Frequency Agile Radar. Sensors 2020, 20, 2176. https://doi.org/10.3390/s20082176
Pan J, Zhu Q, Bao Q, Chen Z. Coherent Integration Method Based on Radon-NUFFT for Moving Target Detection Using Frequency Agile Radar. Sensors. 2020; 20(8):2176. https://doi.org/10.3390/s20082176
Chicago/Turabian StylePan, Jiameng, Qian Zhu, Qinglong Bao, and Zengping Chen. 2020. "Coherent Integration Method Based on Radon-NUFFT for Moving Target Detection Using Frequency Agile Radar" Sensors 20, no. 8: 2176. https://doi.org/10.3390/s20082176





