2D-DOD and 2D-DOA Estimation for a Mixture of Circular and Strictly Noncircular Sources Based on L-Shaped MIMO Radar
Abstract
:1. Introduction
- (1)
- A general model including a mixture of circular and strictly noncircular sources is built for the L-shaped bistatic MIMO radar by stacking received data vector and its conjugated counterpart. Four NC-based direction matrices are then constructed and by joint diagonalization an ESPRIT-like algorithm is developed employing four block selection matrices.
- (2)
- The proposed algorithm can work in the case of common 1D DODs and DOAs, and automatically pair the 4D angle parameters.
- (3)
- The asymptotic performance of the proposed algorithm is analyzed, and the stochastic Cramer–Rao bound (CRB) for the problem is derived with a closed-form expression to serve as the performance benchmark.
2. General Signal Model
3. The Proposed Algorithm
4. Performance Analysis
4.1. Asymptotic Performance Analysis
4.2. Stochastic Cramer–Rao Bound
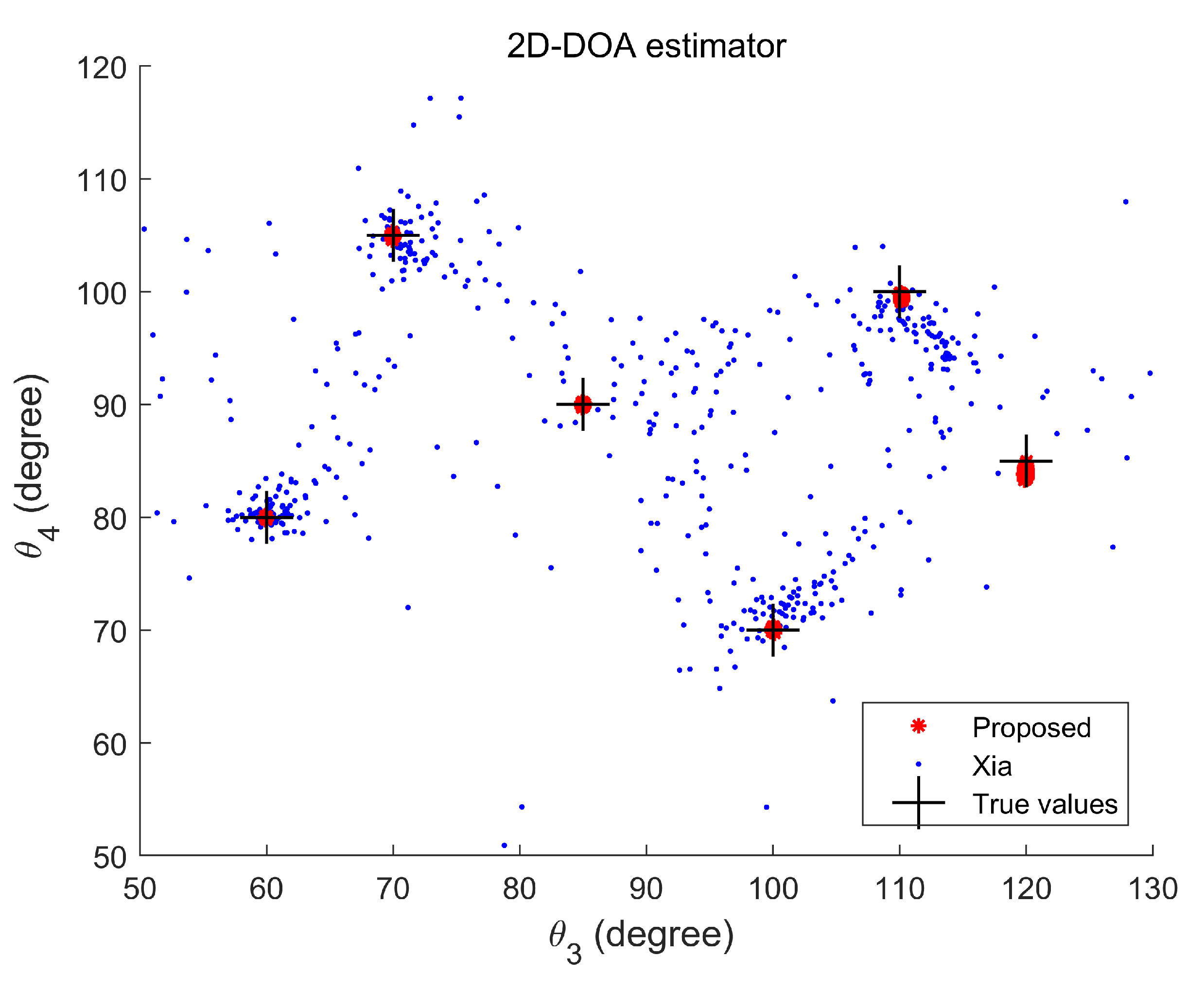
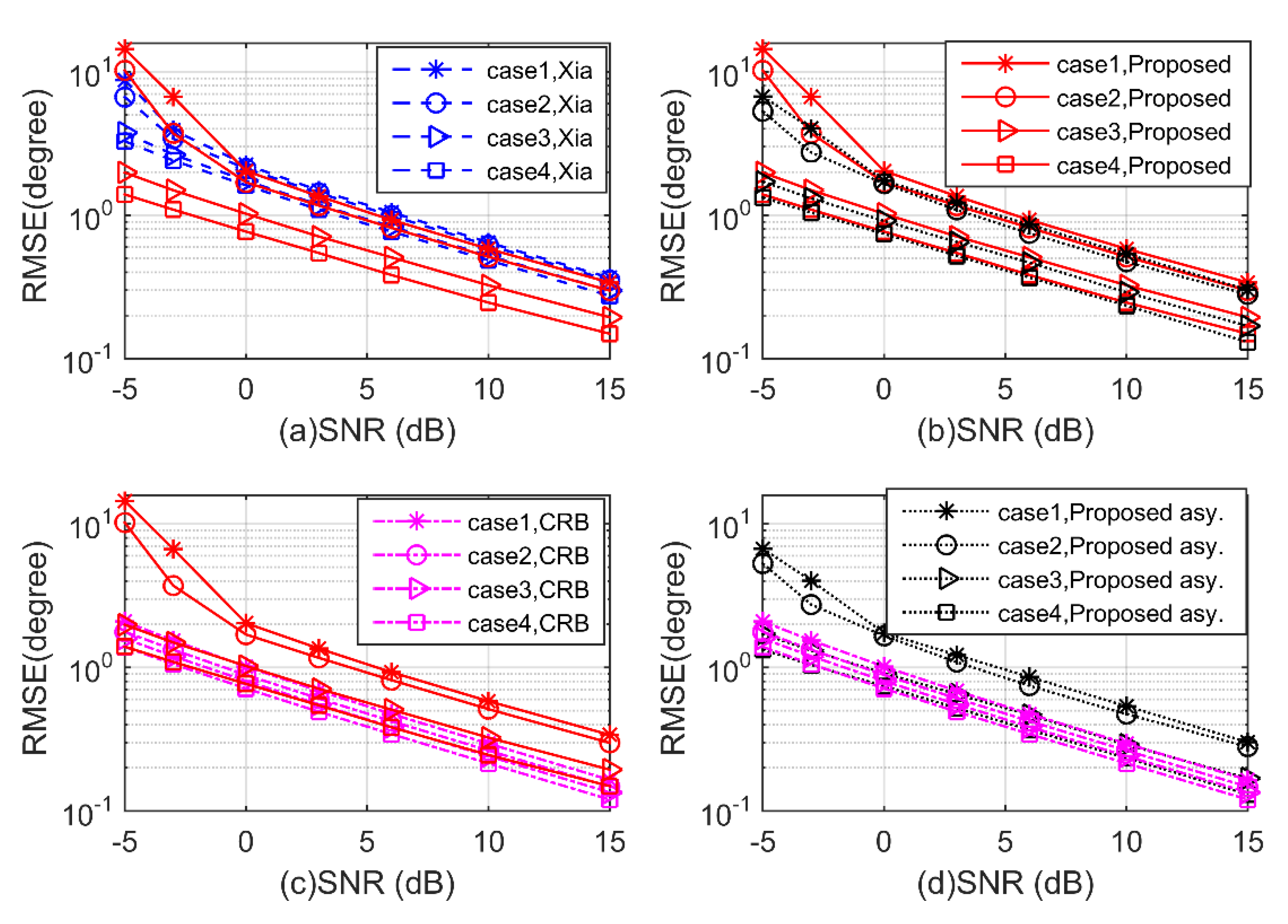
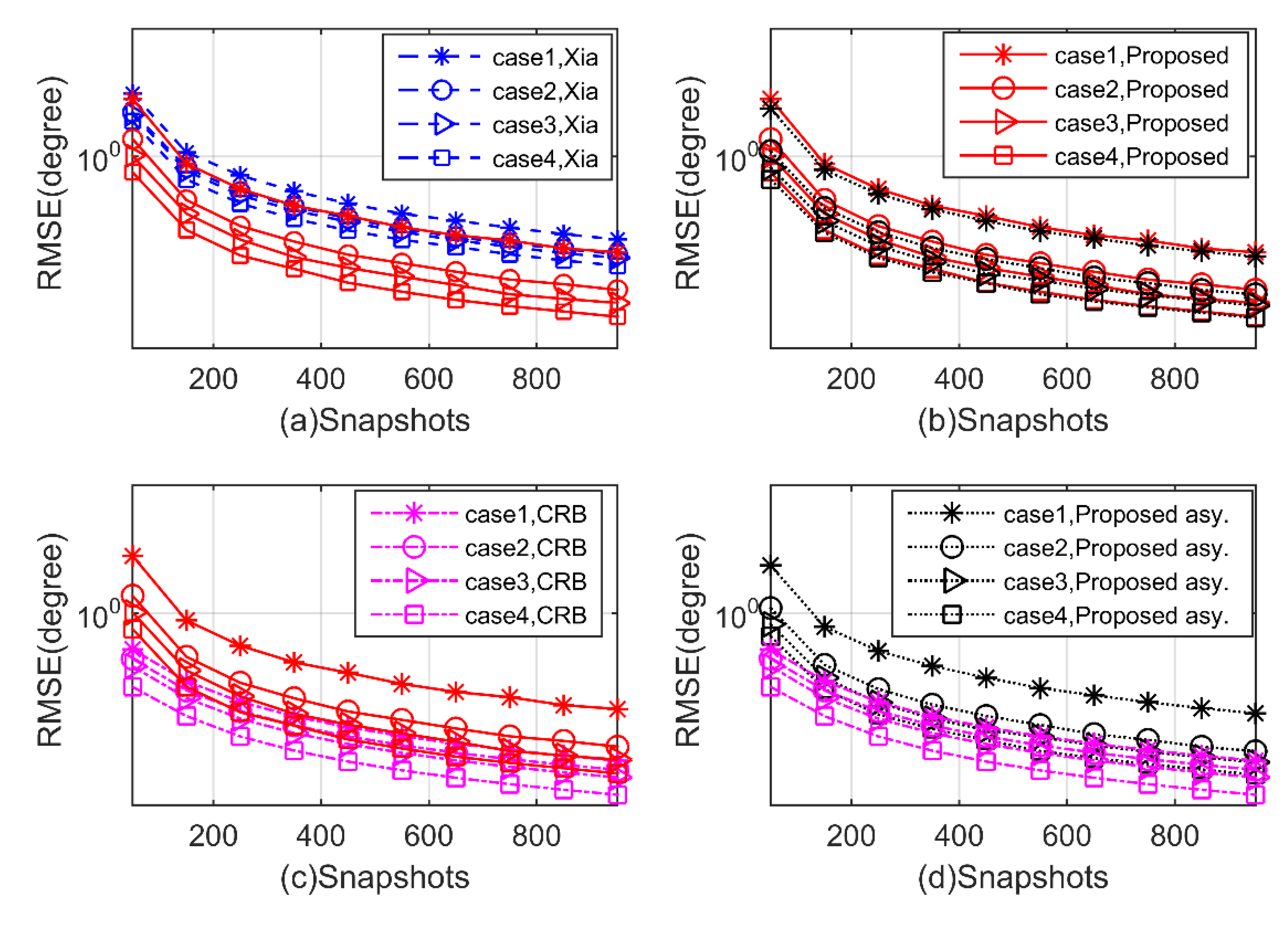
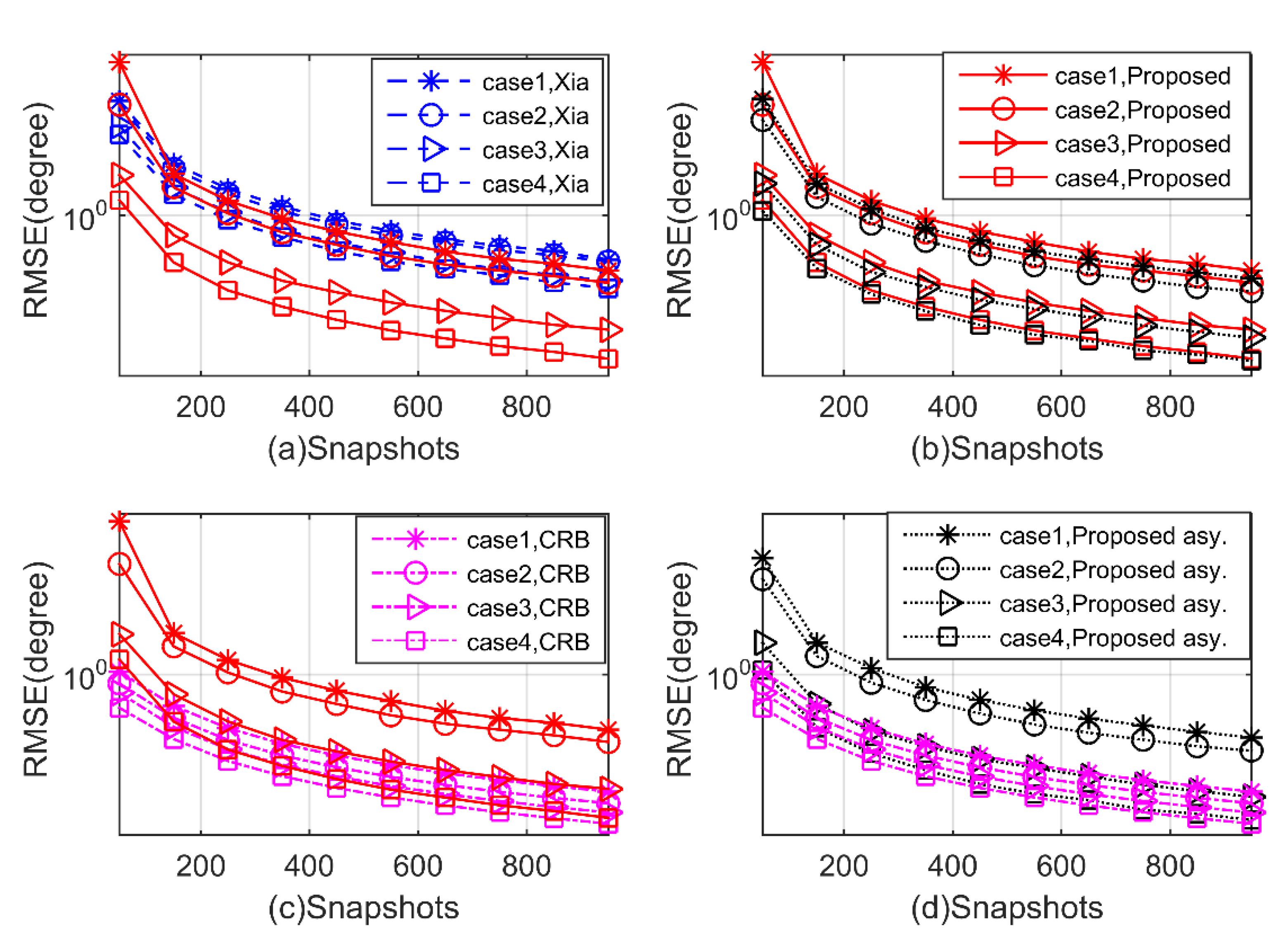
5. Simulation Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, W.; Liu, W.; Wang, J.; Wu, S. Joint Transmission and Reception Diversity Smoothing for Direction Finding of Coherent Targets in MIMO Radar. IEEE J. Sel. Top. Signal Process. 2014, 8, 115–124. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Hu, G.; Zhang, X.; Sun, F. Sparsity-Based DOA Estimation of Coherent and Uncorrelated Targets With Flexible MIMO Radar. IEEE Trans. Veh. Technol. 2019, 68, 5835–5848. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J.; Zhang, Z. Joint 2D-DOD, 2D-DOA, and Polarization Angles Estimation for Bistatic EMVS-MIMO Radar via PARAFAC Analysis. IEEE Trans. Veh. Technol. 2020, 69, 1626–1638. [Google Scholar] [CrossRef]
- Liao, B. Fast Angle Estimation for MIMO Radar with Nonorthogonal Waveforms. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 2091–2096. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Fan, X.; Shi, Z.; Mao, G.; Zhang, Y.D. Direction-of-Arrival Estimation for Coprime Array via Virtual Array Interpolation. IEEE Trans. Signal Process. 2018, 66, 5956–5971. [Google Scholar] [CrossRef]
- Wen, F.; Zhang, Z.; Zhang, G. Joint DOD and DOA Estimation for Bistatic MIMO Radar: A Covariance Trilinear Decomposition Perspective. IEEE Access 2019, 7, 53273–53283. [Google Scholar] [CrossRef]
- Shi, Z.; Zhou, C.; Gu, Y.; Goodman, N.A.; Qu, F. Source Estimation Using Coprime Array: A Sparse Reconstruction Perspective. IEEE Sens. J. 2017, 17, 755–765. [Google Scholar] [CrossRef]
- Li, J.; Jiang, D.; Zhang, X. DOA Estimation Based on Combined Unitary ESPRIT for Coprime MIMO Radar. IEEE Commun. Lett. 2017, 21, 96–99. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; He, S.; Shi, Z. A Robust and Efficient Algorithm for Coprime Array Adaptive Beamforming. IEEE Trans. Veh. Technol. 2018, 67, 1099–1112. [Google Scholar] [CrossRef]
- Wen, F. Computationally Efficient DOA Estimation Algorithm for MIMO Radar with Imperfect Waveforms. IEEE Commun. Lett. 2019, 23, 1037–1040. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L.; Xu, L.; Xu, D. Direction of Departure (DOD) and Direction of Arrival (DOA) Estimation in MIMO Radar with Reduced-Dimension MUSIC. IEEE Commun. Lett. 2010, 14, 1161–1163. [Google Scholar] [CrossRef]
- Bencheikh, M.L.; Wang, Y.; He, H. Polynomial root finding technique for joint DOA DOD estimation in bistatic MIMO radar. Signal Process. 2010, 90, 2723–2730. [Google Scholar] [CrossRef]
- Duofang, C.; Baixiao, C.; Guodong, Q. Angle estimation using ESPRIT in MIMO radar. Electron. Lett. 2008, 44, 770–771. [Google Scholar] [CrossRef]
- Zheng, G.; Chen, B.; Yang, M. Unitary ESPRIT algorithm for bistatic MIMO radar. Electron. Lett. 2012, 48, 179–181. [Google Scholar] [CrossRef]
- Xia, T.Q. Joint diagonalization based DOD and DOA estimation for bistatic MIMO radar. Signal Process. 2015, 108, 159–166. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X. Closed-form blind 2D-DOD and 2D-DOA estimation for MIMO radar with arbitrary arrays. Wirel. Pers. Commun. 2013, 69, 175–186. [Google Scholar] [CrossRef]
- Xia, T.Q. Joint diagonalization based 2D-DOD and 2D-DOA estimation for bistatic MIMO radar. Signal Process. 2015, 116, 7–12. [Google Scholar] [CrossRef]
- Chintagunta, S.; Ponnusamy, P. 2D-DOD and 2D-DOA estimation using the electromagnetic vector sensors. Signal Process. 2018, 147, 163–172. [Google Scholar] [CrossRef]
- Chen, H.; Liu, W.; Zhu, W.P.; Swamy, M.N.S.; Wang, Q. Mixed rectilinear sources localization under unknown mutual coupling. J. Frankl. Inst. (Elsevier) 2019, 356, 2372–2394. [Google Scholar] [CrossRef] [Green Version]
- Abeida, H.; Delmas, J.P. Direct derivation of the stochastic CRB of DOA estimation for rectilinear sources. IEEE Signal Process. Lett. 2017, 24, 1522–1526. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Wan, L.; Huang, M.; Shen, C.; Zhang, K. Polarization Channel Estimation for Circular and Non-Circular Signals in Massive MIMO Systems. IEEE J. Sel. Top. Signal Process. 2019, 13, 1001–1016. [Google Scholar] [CrossRef]
- Chen, H.; Wang, W.; Liu, W. Joint DOA, Range, and Polarization Estimation for Rectilinear Sources with a COLD Array. IEEE Wirel. Commun. Lett. 2019, 8, 1398–1401. [Google Scholar] [CrossRef]
- Wang, X.; Wan, L.; Huang, M.; Shen, C.; Han, Z.; Zhu, T. Low-Complexity Channel Estimation for Circular and Noncircular Signals in Virtual MIMO Vehicle Communication Systems. IEEE Trans. Veh. Technol. 2020. [Google Scholar] [CrossRef]
- Bencheikh, M.L.; Wang, Y. Non circular ESPRIT-Root MUSIC joint DOA-DOD estimation in bistatic MIMO radar. In Proceedings of the International Workshop on Systems, Signal Processing and their Applications, Tipaza, Algeria, 9–11 May 2011; pp. 9–11. [Google Scholar]
- Guo, Y.D.; Zhang, Y.S.; Gong, J.; Zheng, G.M. Direction Finding with Real-Valued ESPRIT for Noncircular Signal in Bistatic MIMO Radar. Wirel. Pers. Commun. 2017, 95, 3321–3332. [Google Scholar] [CrossRef]
- Zheng, G.M.; Tang, J.; Yang, X. ESPRIT and Unitary ESPRIT Algorithms for Coexistence of Circular and Noncircular Signals in Bistatic MIMO Radar. IEEE Access. 2016, 4, 7232–7240. [Google Scholar] [CrossRef]
- Steinwandt, J.; Roemer, F.; Haardt, M. ESPRIT-type algorithms for a received mixture of circular and strictly non-circular signals. In Proceedings of the IEEE Int. Conference on Acoustics, Speech, and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 2809–2813. [Google Scholar]
- Chen, H.; Hou, C.P.; Zhu, W.P.; Liu, W.; Dong, Y.Y.; Peng, Z.J.; Wang, Q. ESPRIT-like two-dimensional direction finding for mixed circular and strictly noncircular sources based on joint diagonalization. Signal Process. (Elsevier) 2017, 141, 48–56. [Google Scholar] [CrossRef] [Green Version]
- Zhou, C.; Gu, Y.; Zhang, Y.D.; Shi, Z.; Jin, T.; Wu, X. Compressive Sensing based Coprime Array Direction-of-Arrival Estimation. IET Commun. 2017, 11, 1719–1724. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, W.P.; Liu, W.; Swamy MN, S.; Li, Y.; Wang, Q.; Peng, Z. RARE-based localization for mixed near-field and far-field rectilinear sources. Digit. Signal Process. 2019, 85, 54–61. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Shi, Z.; Zhang, Y.D. Off-Grid Direction-of-Arrival Estimation Using Coprime Array Interpolation. IEEE Signal Process. Lett. 2018, 25, 1710–1714. [Google Scholar] [CrossRef]
- Zhou, C.; Shi, Z.; Gu, Y.; Shen, X. DECOM: DOA Estimation with Combined MUSIC for Coprime Array. In Proceedings of the International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 24–26 October 2013; pp. 1–5. [Google Scholar]
- Zheng, Z.; Wang, W.; Meng, H.; So, H.C.; Zhang, H. Efficient beamspace-based algorithm for two-dimensional DOA estimation of incoherently distributed sources in massive MIMO systems. IEEE Trans. Veh. Technol. 2018, 67, 11776–11789. [Google Scholar] [CrossRef]
- Zhou, C.; Zhou, J. Direction-of-arrival estimation with coarray ESPRIT for coprime array. Sensors 2017, 17, 1779. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, H.; Wang, W.; Liu, W. Augmented Quaternion ESPRIT-Type DOA Estimation with a Crossed-Dipole Array. IEEE Commun. Lett. 2020, 24, 548–552. [Google Scholar] [CrossRef]
- Belouchrani, A.; Abed-Meraim, K.; Cardoso, J.F.; Moulines, E. A blind source separation technique using second-order statistics. IEEE Trans. Signal Process. 1997, 45, 434–444. [Google Scholar] [CrossRef] [Green Version]
- Dong, Y.; Dong, C.; Zhu, Y.; Zhao, G.; Liu, S. Two-dimensional DOA estimation for L-shaped array with nested subarrays without pair matching. IET Signal Process. 2016, 10, 1112–1117. [Google Scholar] [CrossRef]
- Rao, B.D.; Hari, K.V.S. Performance analysis of ESPRIT and TAM in determining the direction of arrival of plane waves in noise. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1990–1995. [Google Scholar] [CrossRef]
- Li, F.; Vaccaro, R.J.; Tufts, D.W. Performance analysis of the state-space realization (TAM) and ESPRIT algorithms for DOA estimation. IEEE Trans. Antennas Propag. 1991, 39, 418–423. [Google Scholar] [CrossRef]
- Stoica, P.; Larsson, A.G.; Gershman, A.B. The stochastic CRB for array processing: A textbook derivation. IEEE Signal Process. Lett. 2001, 8, 148–150. [Google Scholar] [CrossRef]
- Wen, F.; Wang, J.; Shi, J.; Gui, G. Auxiliary Vehicle Positioning Based on Robust DOA Estimation with Unknown Mutual Coupling. IEEE Internet Things J. 2020. [Google Scholar] [CrossRef]
- He, J.; Swamy, M.N.S.; Ahmad, M.O. Efficient Application of MUSIC Algorithm Under the Coexistence of Far-Field and Near-Field Sources. IEEE Trans. Signal Process. 2012, 60, 2066–2070. [Google Scholar] [CrossRef]
- Wen, F.; Zhang, X.; Zhang, Z. CRBs for direction-of-departure and direction-of-arrival estimation in collocated MIMO radar in the presence of unknown spatially coloured noise. IET Radar Sonar Navig. 2019, 13, 530–537. [Google Scholar] [CrossRef]

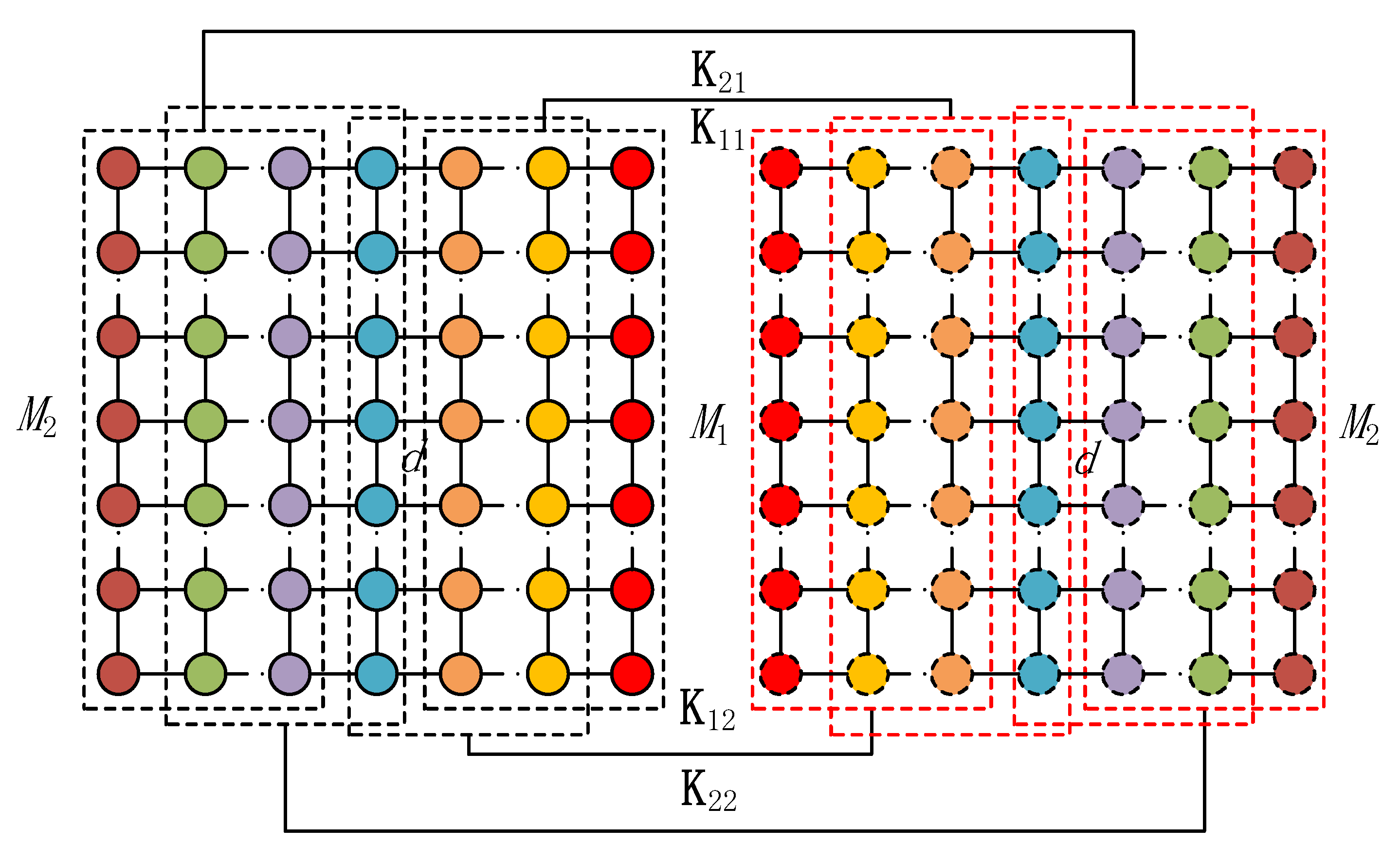
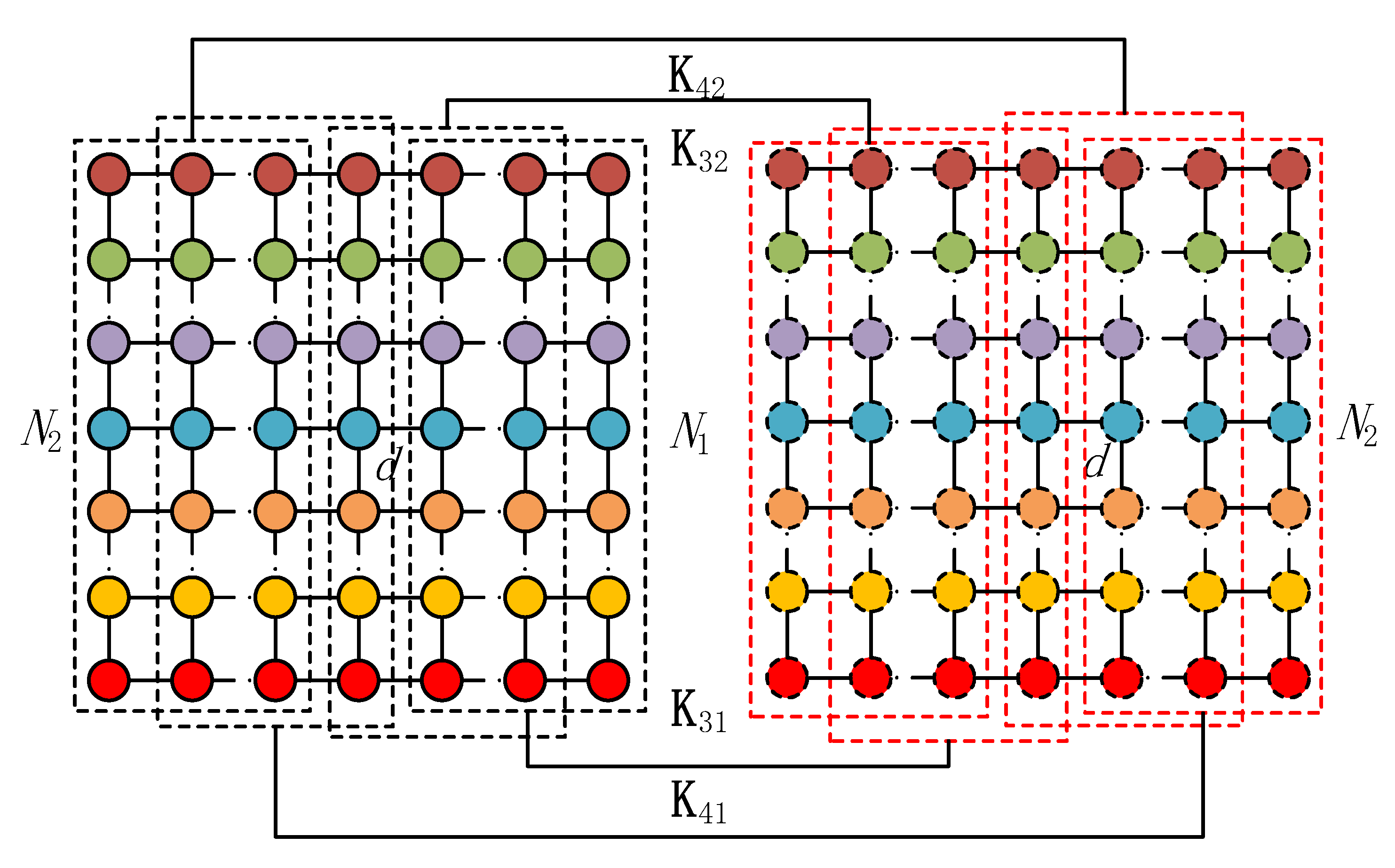


|
Input:
: T snapshots of the new constructed array vector. Output: : pair-free 2D-DODs and 2D-DOAs of K mixed signals |
|---|
| Step 1: Perform SVD on to get , and then compute ; Step 2: Define a set according to Equation (18) Step 3: Implement the joint diagonalization to the set to obtain the unitary matrix by a series of Givens rotations; Step 4: Compute the eigenvalues according to Equation (20), and then compute according to Equation (21); Step 5: Compute the 2-D DODs and 2-D DOAs of circular signals according to Equation (22). |
| Algorithm | Angle | Maximum Number |
|---|---|---|
| Proposed algorithm | DOD | |
| DOA | ||
| Xia’s algorithm | DOD | |
| DOA |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, J.; Liu, Y.; Jiang, Y.; Lu, Y.; Zhang, Z.; Chen, H.; Wang, L. 2D-DOD and 2D-DOA Estimation for a Mixture of Circular and Strictly Noncircular Sources Based on L-Shaped MIMO Radar. Sensors 2020, 20, 2177. https://doi.org/10.3390/s20082177
Fang J, Liu Y, Jiang Y, Lu Y, Zhang Z, Chen H, Wang L. 2D-DOD and 2D-DOA Estimation for a Mixture of Circular and Strictly Noncircular Sources Based on L-Shaped MIMO Radar. Sensors. 2020; 20(8):2177. https://doi.org/10.3390/s20082177
Chicago/Turabian StyleFang, Jiaxiong, Yonghong Liu, Yifang Jiang, Yang Lu, Zehao Zhang, Hua Chen, and Laihua Wang. 2020. "2D-DOD and 2D-DOA Estimation for a Mixture of Circular and Strictly Noncircular Sources Based on L-Shaped MIMO Radar" Sensors 20, no. 8: 2177. https://doi.org/10.3390/s20082177
APA StyleFang, J., Liu, Y., Jiang, Y., Lu, Y., Zhang, Z., Chen, H., & Wang, L. (2020). 2D-DOD and 2D-DOA Estimation for a Mixture of Circular and Strictly Noncircular Sources Based on L-Shaped MIMO Radar. Sensors, 20(8), 2177. https://doi.org/10.3390/s20082177





