An Optically Tunable THz Modulator Based on Nanostructures of Silicon Substrates
Abstract
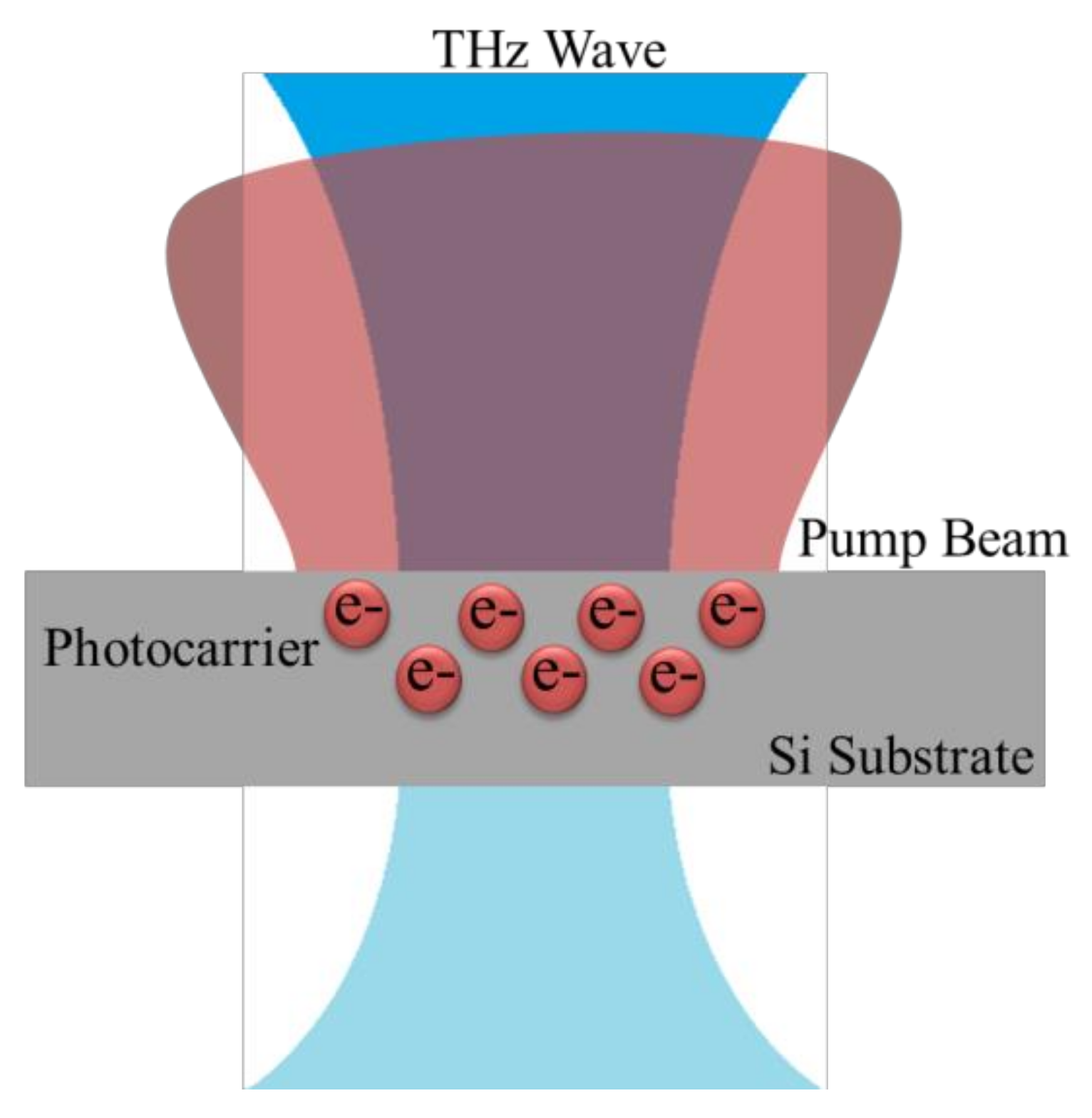
1. Introduction
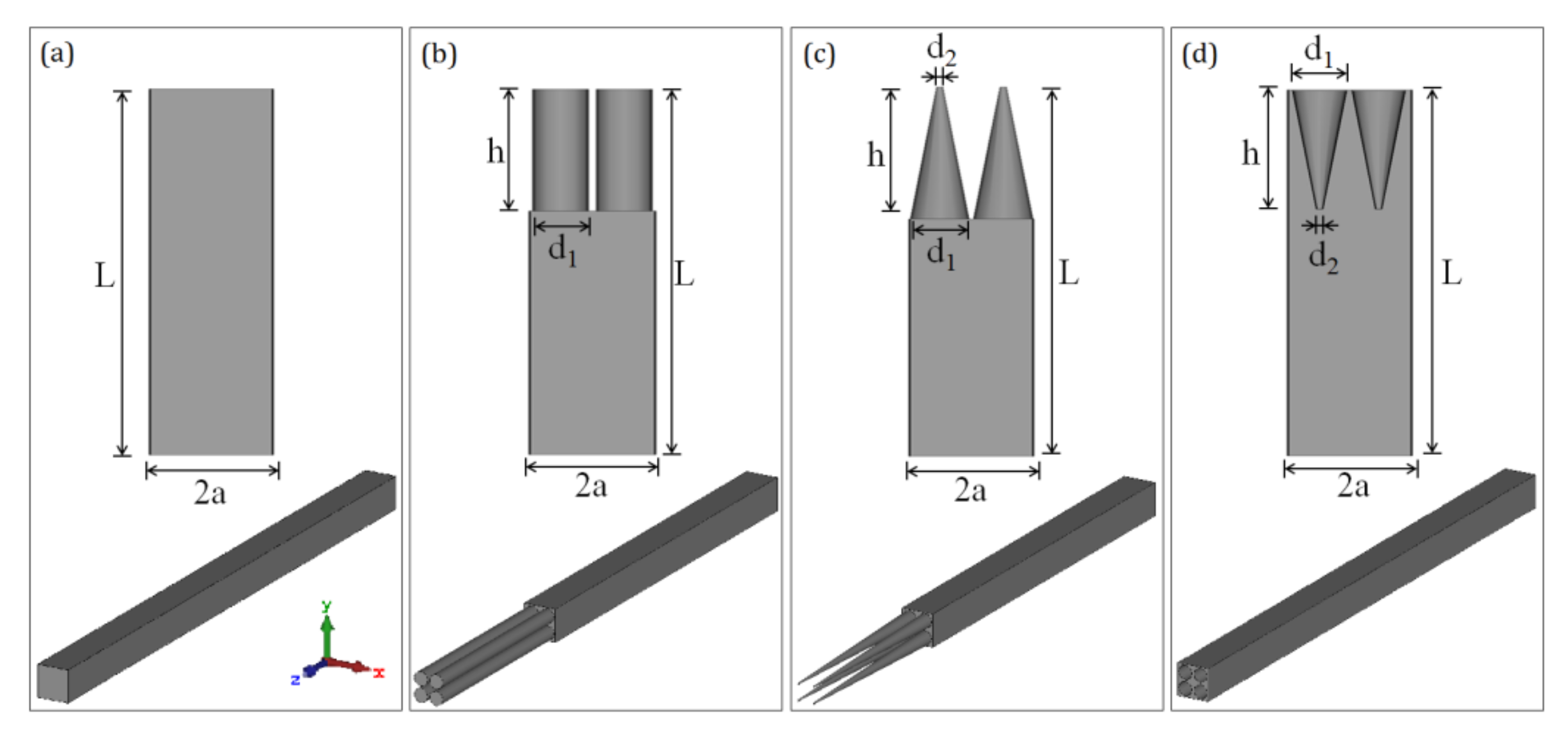
2. Method
3. Results and Discussion
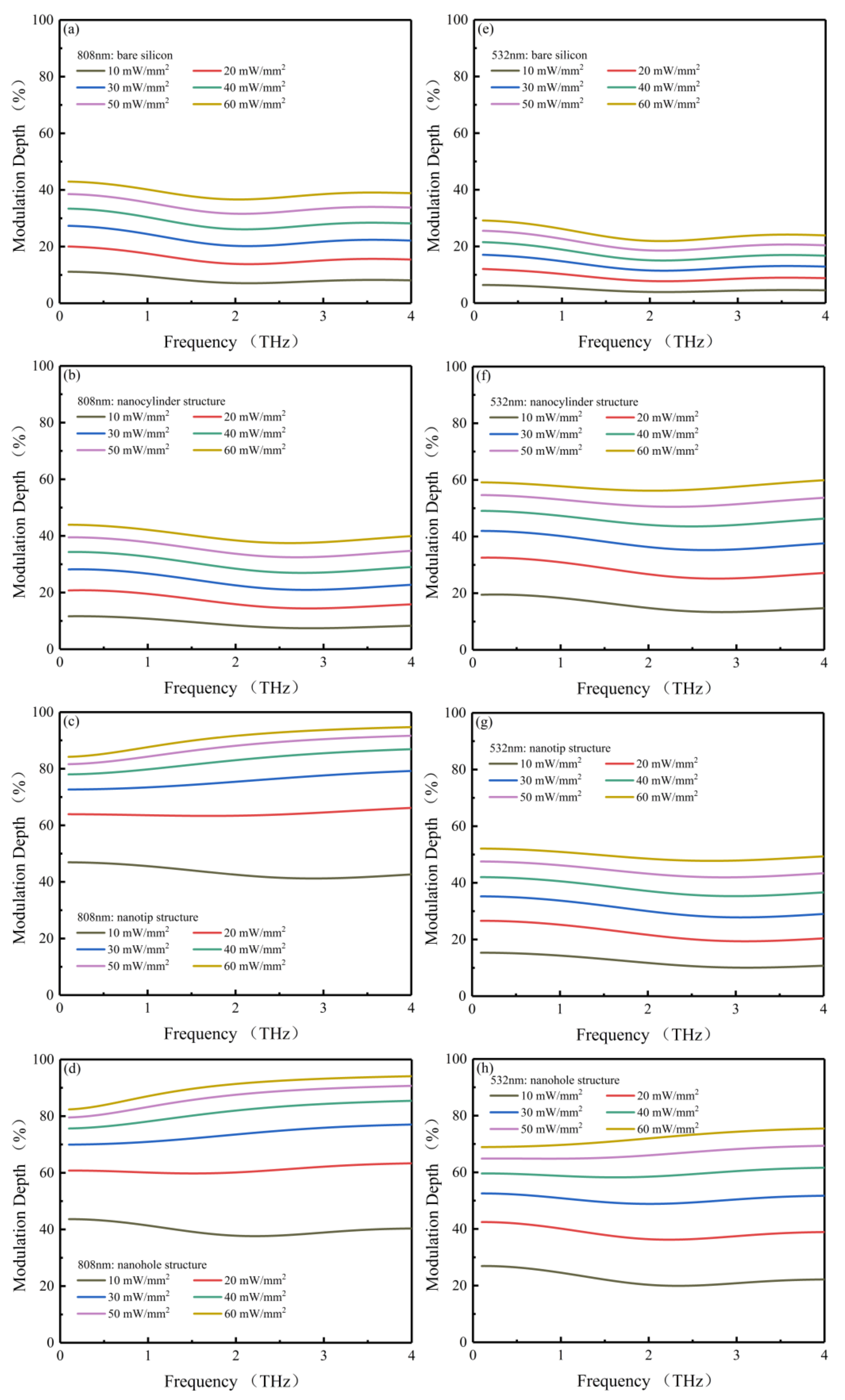
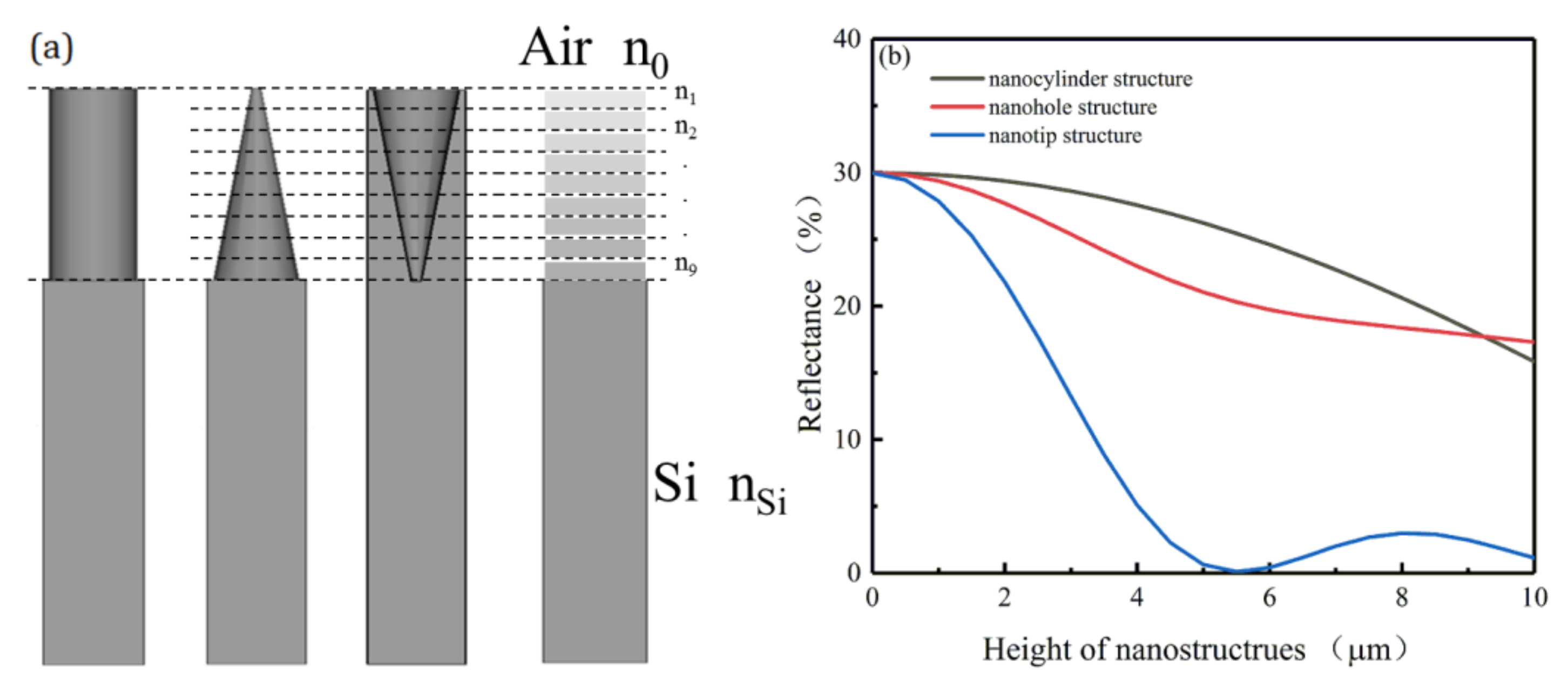
3.1. Simulation Results
3.2. Theoretical Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ullah, Z.; Witjaksono, G.; Nawi, I.; Tansu, N.; Irfan Khattak, M.; Junaid, M. A review on the development of tunable graphene nanoantennas for terahertz optoelectronic and plasmonic applications. Sensors 2020, 20, 1401. [Google Scholar] [CrossRef] [PubMed]
- Bründermann, E.; Hübers, H.; Kimmitt, M.F. Terahertz Techniques; Springer: Berlin, Germany, 2012. [Google Scholar]
- Kašalynas, I.; Venckevičius, R.; Minkevičius, L.; Sešek, A.; Wahaia, F.; Tamošiūnas, V.; Voisiat, B.; Seliuta, D.; Valušis, G.; Švigelj, A.; et al. Spectroscopic terahertz imaging at room temperature employing microbolometer terahertz sensors and its application to the study of carcinoma tissues. Sensors 2016, 16, 432. [Google Scholar] [CrossRef] [PubMed]
- Degl Innocenti, R.; Kindness, S.J.; Beere, H.E.; Ritchie, D.A. All-integrated terahertz modulators. Nanophotonics 2018, 7, 127–144. [Google Scholar] [CrossRef]
- Hack, E.; Valzania, L.; Gäumann, G.; Shalaby, M.; Hauri, C.; Zolliker, P. Comparison of thermal detector arrays for off-axis THz holography and real-time THz imaging. Sensors 2016, 16, 221. [Google Scholar] [CrossRef]
- He, J.; Zhang, Y. Metasurfaces in terahertz waveband. J. Phys. D Appl. Phys. 2017, 50, 464004. [Google Scholar] [CrossRef]
- Puc, U.; Abina, A.; Jeglič, A.; Zidanšek, A.; Kašalynas, I.; Venckevičius, R.; Valušis, G. Spectroscopic analysis of melatonin in the terahertz frequency range. Sensors 2018, 18, 4098. [Google Scholar] [CrossRef]
- Alius, H.; Dodel, G. Amplitude-, phase-, and frequency modulation of far-infrared radiation by optical excitation of silicon. Infrared Phys. 1991, 32, 1–11. [Google Scholar] [CrossRef]
- Vogel, T.; Dodel, G.; Holzhauer, E.; Salzmann, H.; Theurer, A. High-speed switching of far-infrared radiation by photoionization in a semiconductor. Appl. Opt. 1992, 31, 329–337. [Google Scholar] [CrossRef]
- Okada, T.; Tanaka, K. Photo-designed terahertz devices. Sci. Rep. 2011, 1, 121. [Google Scholar] [CrossRef]
- Xie, Z.; Wang, X.; Ye, J.; Feng, S.; Sun, W.; Akalin, T.; Zhang, Y. Spatial terahertz modulator. Sci. Rep. 2013, 3, 3347. [Google Scholar] [CrossRef]
- Zhang, B.; Lv, L.; He, T.; Chen, T.; Zang, M.; Zhong, L.; Wang, X.; Shen, J.; Hou, Y. Active terahertz device based on optically controlled organometal halide perovskite. Appl. Phys. Lett. 2015, 107, 093301. [Google Scholar] [CrossRef]
- Cheng, L.J.; Liu, L. Optical modulation of continuous terahertz waves towards cost-effective reconfigurable quasi-optical terahertz components. Opt. Express 2013, 21, 28657. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Qiao, H.; Huangfu, H.; Li, X.; Guo, J.; Wang, H. Optical absorption of several nanostructures arrays for silicon solar cells. Opt. Commun. 2015, 356, 526–529. [Google Scholar] [CrossRef]
- Zhu, J.; Yu, Z.; Burkhard, G.F.; Hsu, C.M.; Connor, S.T.; Xu, Y.; Wang, Q.; McGehee, M.; Fan, S.; Cui, Y. Optical absorption enhancement in amorphous silicon nanowire and nanocone arrays. Nano Lett. 2009, 9, 279–282. [Google Scholar] [CrossRef]
- Lin, H.; Xiu, F.; Fang, M.; Yip, S.; Cheung, H.Y.; Wang, F.; Han, N.; Chan, K.S.; Wong, C.Y.; Ho, J.C. Rational design of inverted nanopencil arrays for cost-effective, broadband, and omnidirectional light harvesting. ACS Nano 2014, 8, 3752–3760. [Google Scholar] [CrossRef]
- Li, G.; Kwok, H.S. Silicon nanowire solar cells. In Advances in Silicon Solar Cells; Ikhmayies, S., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 269–298. [Google Scholar]
- Shi, Z.; Cao, X.; Wen, Q.; Wen, T.; Yang, Q.; Chen, Z.; Shi, W.; Zhang, H. Terahertz modulators based on silicon nanotip array. Adv. Opt. Mater. 2018, 6, 1700620. [Google Scholar] [CrossRef]
- Wu, X.; Pan, X.; Quan, B.; Wang, L. Optical modulation of terahertz behavior in silicon with structured surfaces. Appl. Phys. Lett. 2013, 103, 121112. [Google Scholar] [CrossRef]
- Kelzenberg, M.D.; Boettcher, S.W.; Petykiewicz, J.A.; Turner-Evans, D.B.; Putnam, M.C.; Warren, E.L.; Spurgeon, J.M.; Briggs, R.M.; Lewis, N.S.; Atwater, H.A. Erratum: Enhanced absorption and carrier collection in Si wire arrays for photovoltaic applications. Nat. Mater. 2010, 9, 239–244. [Google Scholar] [CrossRef]
- Kupec, J.; Stoop, R.L.; Witzigmann, B. Light absorption and emission in nanowire array solar cells. Opt. Express 2010, 18, 27589–27605. [Google Scholar] [CrossRef]
- Garnett, E.; Yang, P. Light trapping in silicon nanowire solar cells. Nano Lett 2010, 10, 1082–1087. [Google Scholar] [CrossRef]
- Jung, J.Y.; Guo, Z.; Jee, S.W.; Um, H.D.; Park, K.T.; Lee, J.H. A strong antireflective solar cell prepared by tapering silicon nanowires. Opt. Express 2010, 18 (Suppl. S3), A286–A292. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Lal, A. High-efficiency ordered silicon nano-conical-frustum array solar cells by self-powered parallel electron lithography. Nano Lett. 2010, 10, 4651–4656. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yuan, M.; Chen, L.; Cai, B.; Yang, R.; Zhu, Y. Broadband terahertz anti-reflective structure fabricated by femtosecond laser drilling technique. Opt. Commun. 2016, 361, 148–152. [Google Scholar] [CrossRef]
- Yang, D.; Jiang, T.; Cheng, X. Optically controlled terahertz modulator by liquid-exfoliated multilayer WS2 nanosheets. Opt. Express 2017, 25, 16364–16377. [Google Scholar] [CrossRef] [PubMed]
- Edwards, D.F. Silicon (Si). In Handbook of Optical Constants of Solids; Palik, E.D., Ed.; Academic Press: Cambridge, MA, USA, 1985. [Google Scholar]
- Auslender, M.; Hava, S. Doped n-Type Silicon (n-Si). In Handbook of Optical Constants of Solids III; Palik, E.D., Ed.; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Jäger, S.T.; Strehle, S. Design parameters for enhanced photon absorption in vertically aligned silicon nanowire arrays. Nanoscale Res. Lett. 2014, 9, 511. [Google Scholar] [CrossRef]
- Butt, H.; Dai, Q.; Rajasekharan, R.; Wilkinson, T.D.; Amaratunga, G.A.J. Enhanced reflection from arrays of silicon based inverted nanocones. Appl. Phys. Lett. 2011, 99, 133105. [Google Scholar] [CrossRef]
- Li, Q.; Tian, Z.; Zhang, X.; Singh, R.; Du, L.; Gu, J.; Han, J.; Zhang, W. Active graphene–silicon hybrid diode for terahertz waves. Nat. Commun. 2015, 6, 7082. [Google Scholar] [CrossRef]
- Fan, Z.; Geng, Z.; Lv, X.; Su, Y.; Yang, Y.; Liu, J.; Chen, H. Optical controlled terahertz modulator based on tungsten disulfide nanosheet. Sci. Rep. 2017, 7, 14828. [Google Scholar] [CrossRef]
- Cao, Y.; Gan, S.; Geng, Z.; Liu, J.; Yang, Y.; Bao, Q.; Chen, H. Optically tuned terahertz modulator based on annealed multilayer MoS2. Sci. Rep. 2016, 6, 22899. [Google Scholar] [CrossRef]
- Chen, S.; Fan, F.; Miao, Y.; He, X.; Zhang, K.; Chang, S. Ultrasensitive terahertz modulation by silicon-grown MoS2 nanosheets. Nanoscale 2016, 8, 4713–4719. [Google Scholar] [CrossRef]
- Green, M.A.; Keevers, M.J. Optical properties of intrinsic silicon at 300 K. Prog. Photovolt. Res. Appl. 1995, 3, 189–192. [Google Scholar] [CrossRef]
- Green, M.A. Self-consistent optical parameters of intrinsic silicon at 300K including temperature coefficients. Sol. Energ Mater. Sol. Cells 2008, 92, 1305–1310. [Google Scholar] [CrossRef]
- Mak, K.F.; He, K.; Lee, C.; Lee, G.H.; Hone, J.; Heinz, T.F.; Shan, J. Tightly bound trions in monolayer MoS2. Nat. Mater. 2013, 12, 207–211. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Zhang, C.; Chan, W.; Manolatou, C.; Tiwari, S.; Rana, F. Radiative lifetimes of excitons and trions in monolayers of the metal dichalcogenide MoS2. Phys. Rev. B 2016, 93, 045407. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, H.; Chan, W.; Manolatou, C.; Rana, F. Absorption of light by excitons and trions in monolayers of metal dichalcogenide MoS2: Experiments and theory. Phys. Rev. B 2014, 89, 205436. [Google Scholar] [CrossRef]
- Sze, S.M.; Ng, K.K. Physics of Semiconductor Devices; John Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Lowdermilk, W.H.; Milam, D. Graded-index antireflection surfaces for high-power laser applications. Appl. Phys. Lett. 1980, 36, 891–893. [Google Scholar] [CrossRef]
- Lin, G.R.; Meng, F.S.; Pai, Y.H.; Chang, Y.C.; Hsu, S.H. Manipulative depolarization and reflectance spectra of morphologically controlled nano-pillars and nano-rods. Opt. Express 2009, 17, 20824–20832. [Google Scholar] [CrossRef]
- Born, M.; Wolf, E. Principles of Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Macleod, H.A. Thin-Film Optical Filter; Institute of Physics: London, UK, 2001. [Google Scholar]
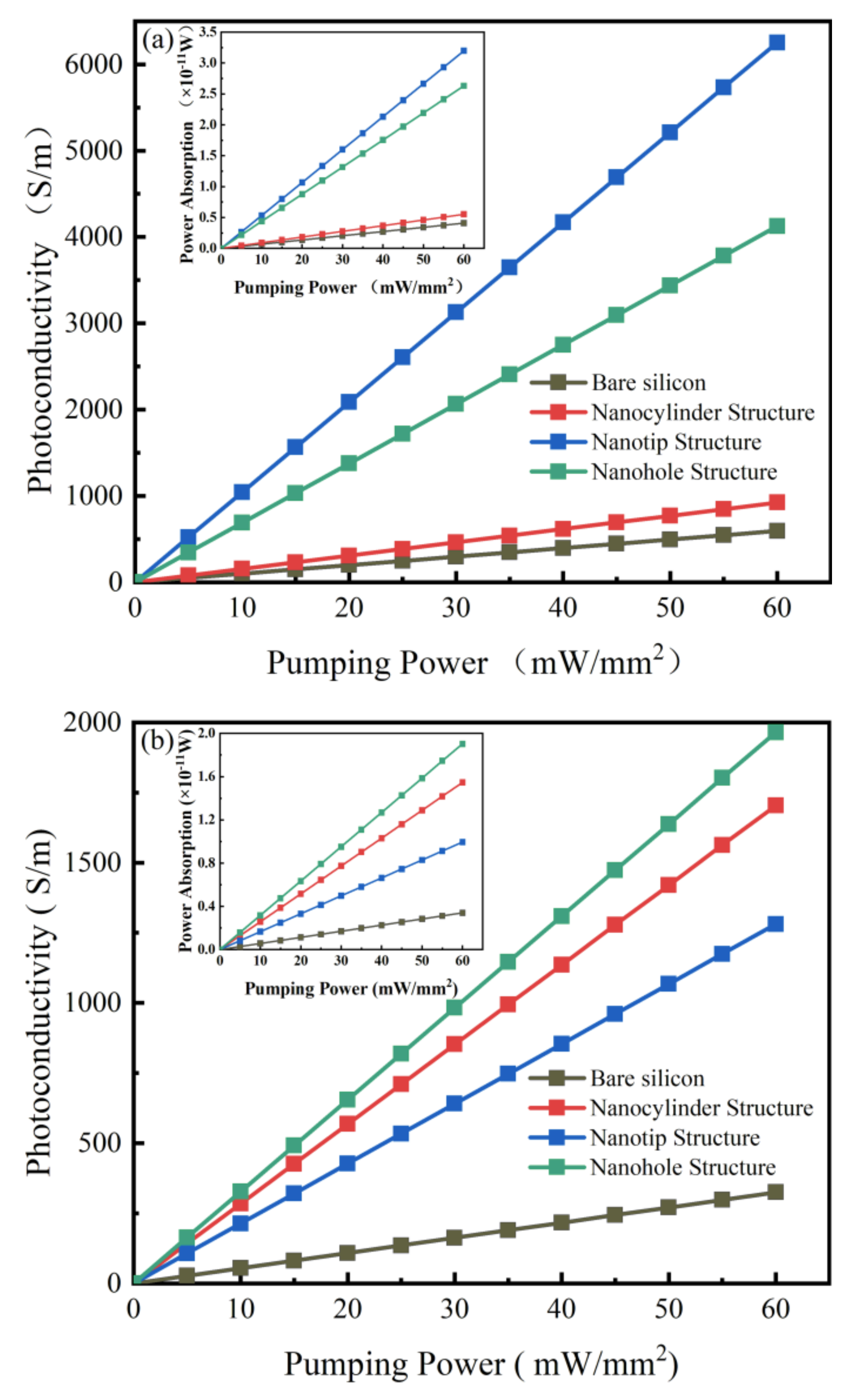

| Wavelength | Bare Silicon | Nanocylinder Structure | Nanotip Structure | Nanohole Structure |
|---|---|---|---|---|
| 808 nm | 594 | 923 | 6253 | 4126 |
| 532 nm | 375 | 1704 | 1281 | 1965 |
| Wavelength | Bare Silicon | Nanocylinder Structure | Nanotip Structure | Nanohole Structure |
|---|---|---|---|---|
| 808 nm | 1.73 | 2.70 | 18.25 | 12.05 |
| 532 nm | 0.95 | 4.97 | 3.74 | 5.74 |
| Wavelength | Bare Silicon | Nanocylinder Structure | Nanotip Structure | Nanohole Structure |
|---|---|---|---|---|
| 808 nm | 51% | 51.63% | 9.13% | 9.69% |
| 532 nm | 63.18% | 36.41% | 42.44% | 23.96% |
| Wavelength | Bare Silicon | Nanocylinder Structure | Nanotip Structure | Nanohole Structure |
|---|---|---|---|---|
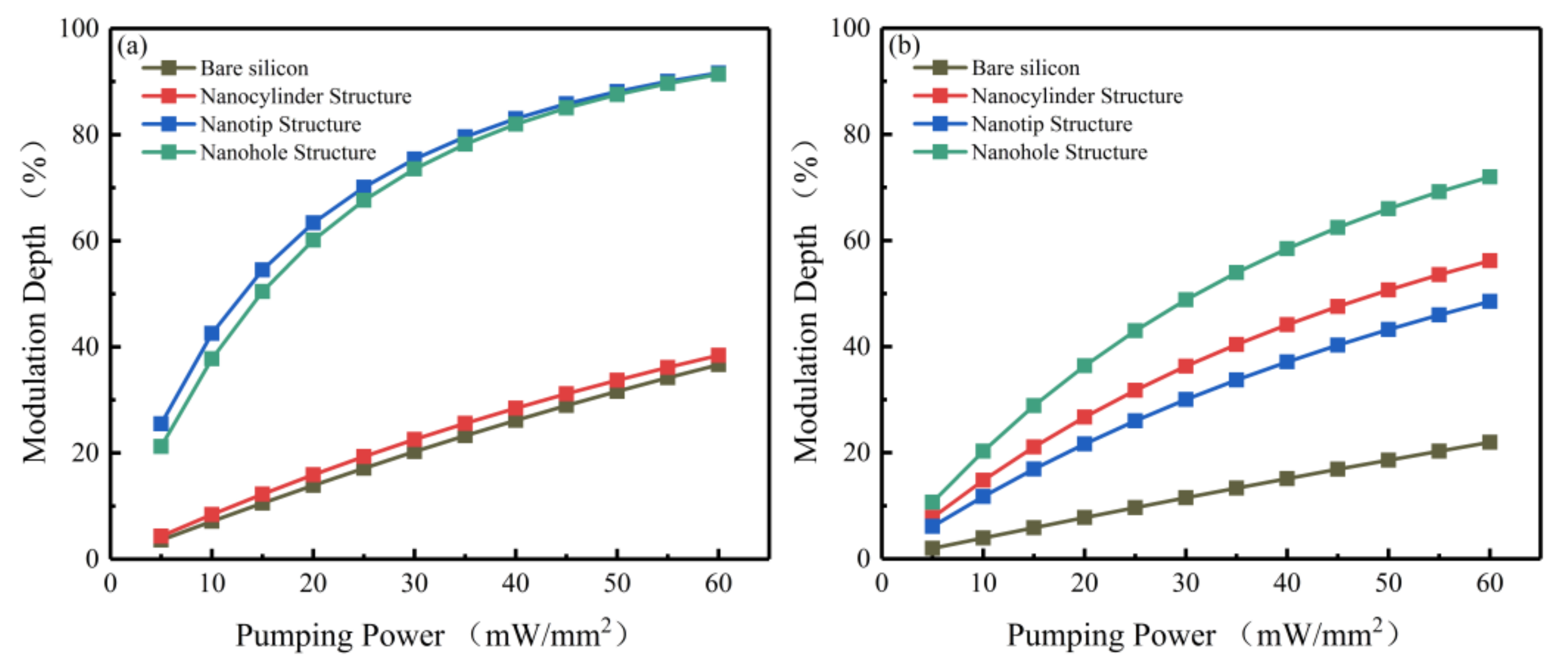
| 808 nm | 8.48% → 38.99% | 9.07% → 39.94% | 43.41% → 90.74% | 39.93% → 90.14% |
| 532 nm | 4.76% → 24.47% | 15.8% → 57.7% | 12.19% → 49.42% | 22.47% → 72.1% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, C.; Liu, J.; Wei, D.; Wu, H.; Wen, Q.; Ling, D. An Optically Tunable THz Modulator Based on Nanostructures of Silicon Substrates. Sensors 2020, 20, 2198. https://doi.org/10.3390/s20082198
Mo C, Liu J, Wei D, Wu H, Wen Q, Ling D. An Optically Tunable THz Modulator Based on Nanostructures of Silicon Substrates. Sensors. 2020; 20(8):2198. https://doi.org/10.3390/s20082198
Chicago/Turabian StyleMo, Chen, Jingbo Liu, Dongshan Wei, Honglei Wu, Qiye Wen, and Dongxiong Ling. 2020. "An Optically Tunable THz Modulator Based on Nanostructures of Silicon Substrates" Sensors 20, no. 8: 2198. https://doi.org/10.3390/s20082198
APA StyleMo, C., Liu, J., Wei, D., Wu, H., Wen, Q., & Ling, D. (2020). An Optically Tunable THz Modulator Based on Nanostructures of Silicon Substrates. Sensors, 20(8), 2198. https://doi.org/10.3390/s20082198







