Research on Turning Motion Targets and Velocity Estimation in High Resolution Spaceborne SAR
Abstract
:1. Introduction
2. Imaging Signatures of Turning Motion Target
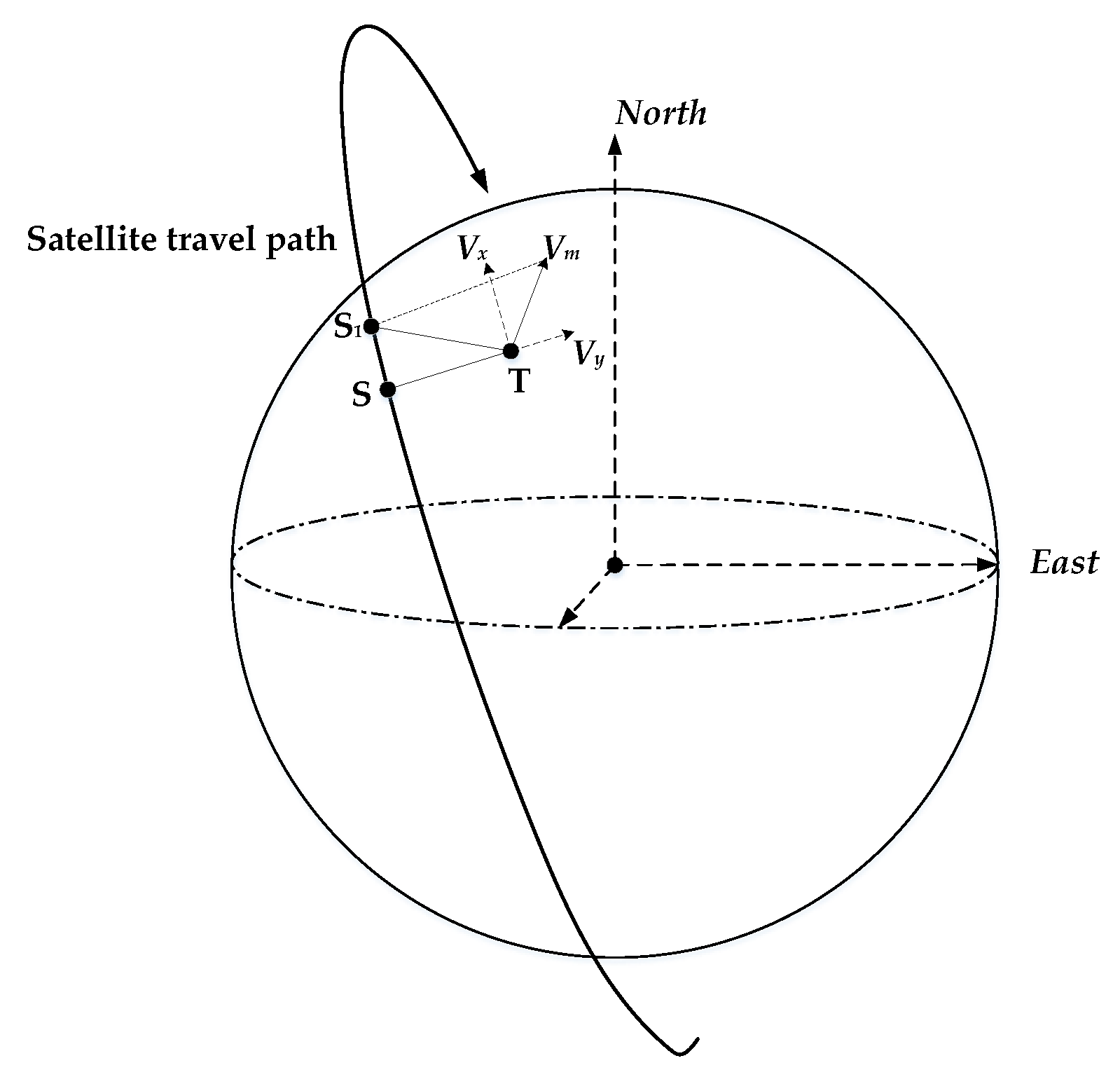
2.1. Analysis of Moving Target with Constant Velocity in Spaceborne SAR
2.1.1. Target Azimuth Delocalization
2.2.2. Target Azimuth Defocusing
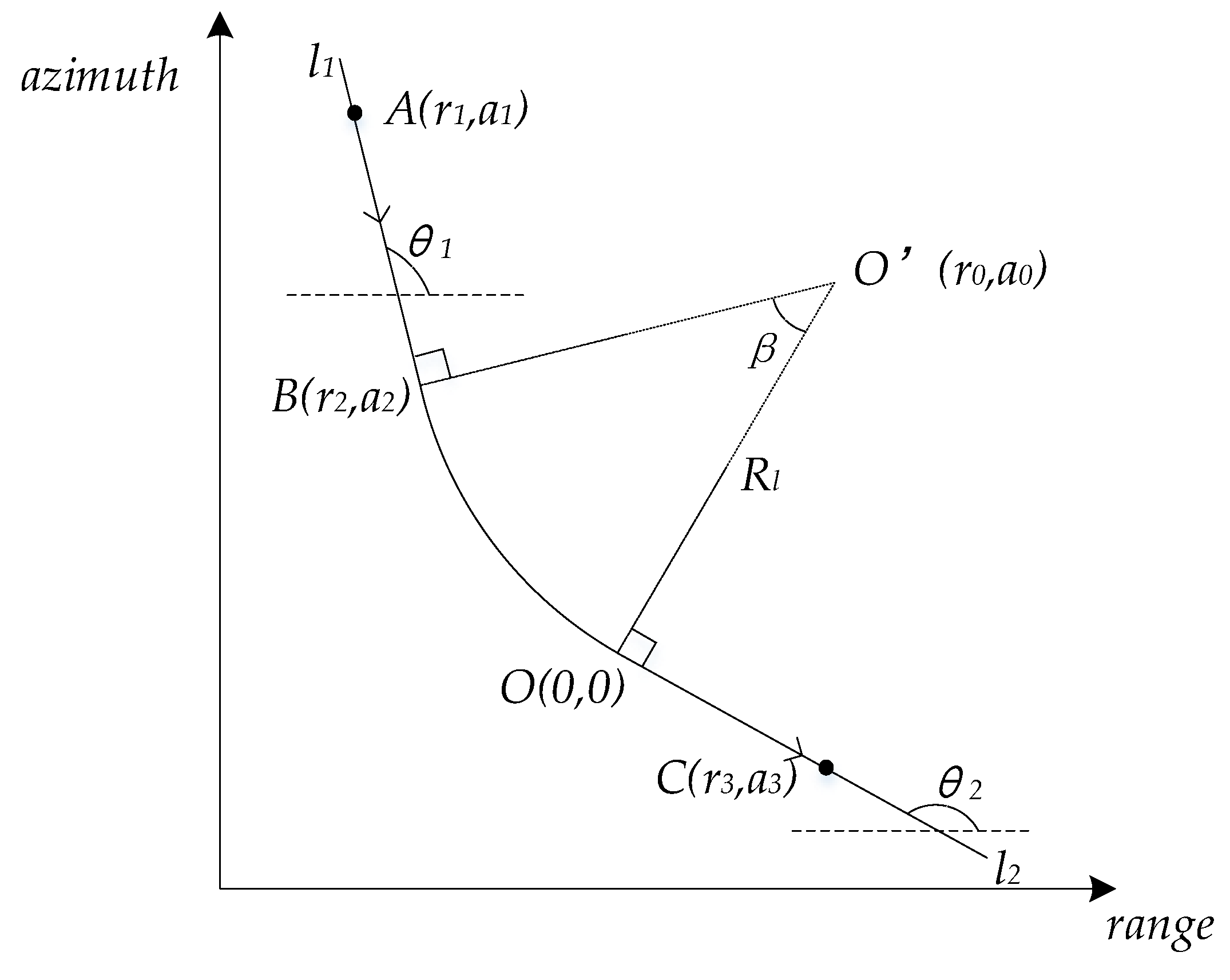
2.2. Analysis of Turning Motion Target
- centering angle of arc part of curve, mark as β;
- radius of the arc part of the curve, mark as Rl;
- slope of line l1 at the beginning of the curve, mark as θ1; and,
- slope of line l2 at the end of the curve, mark as θ2.
3. Moving Target Refocusing and Velocity Estimation of Turning Motion Target
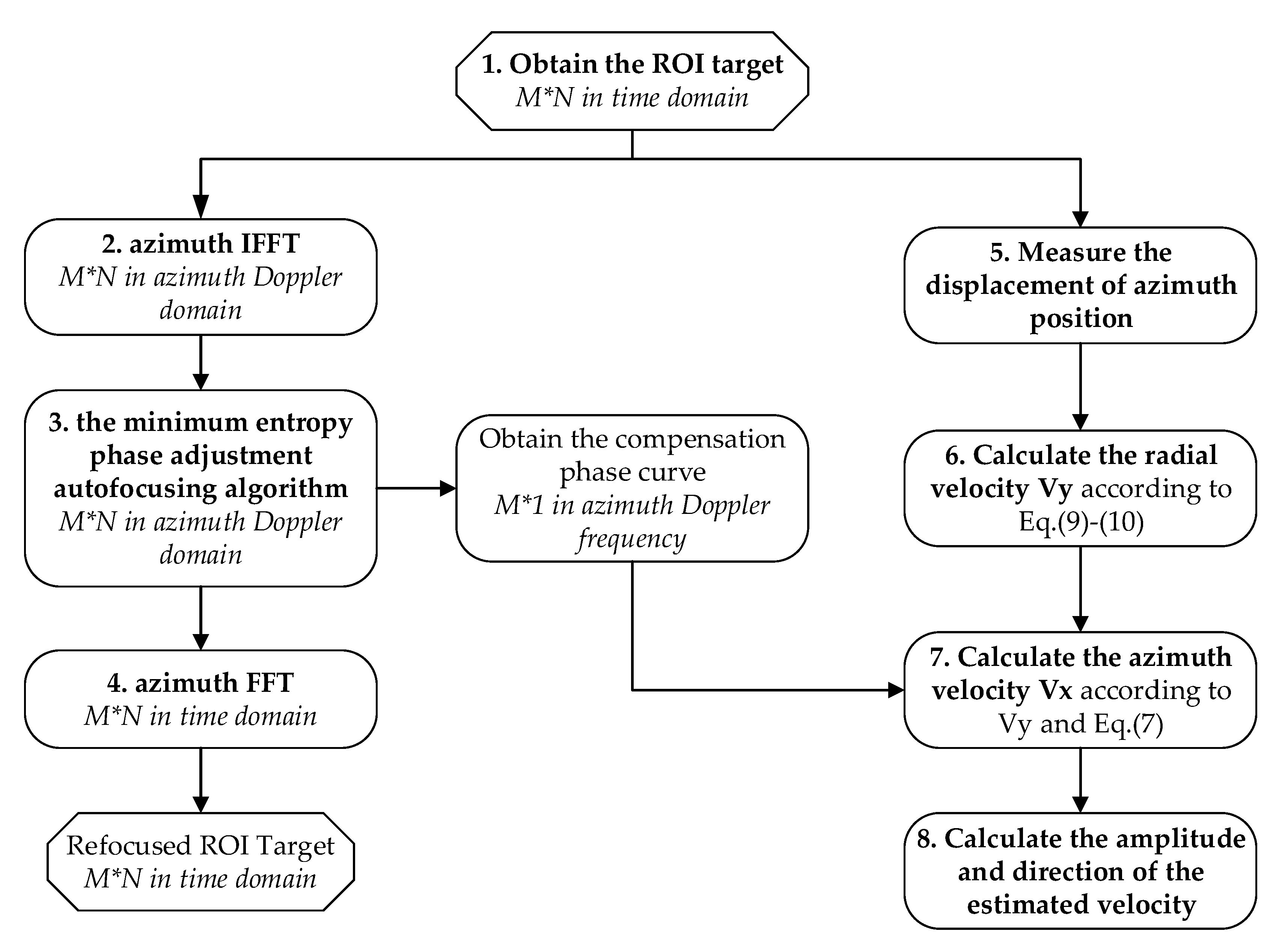
3.1. Motion Compensation Algorithm
3.2. Velocity Estimation Method
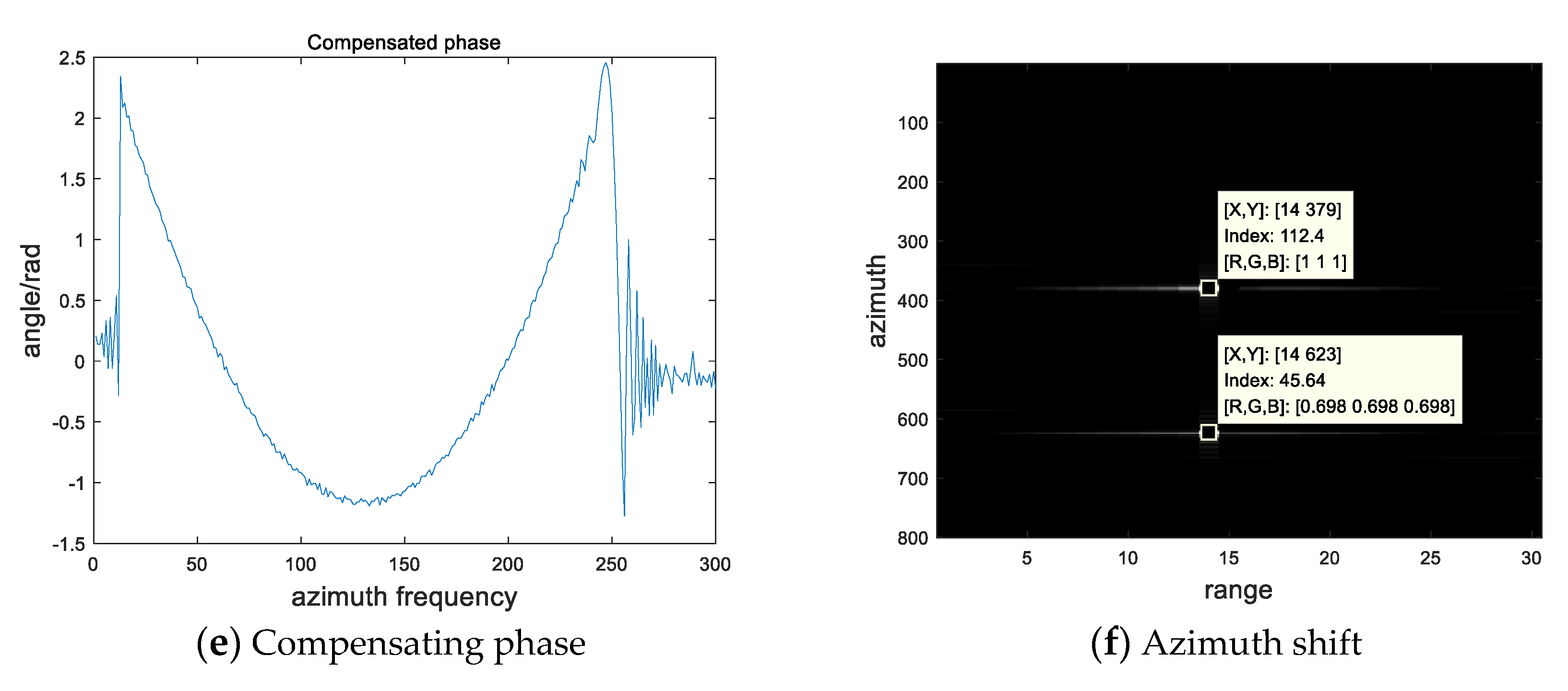
4. Results
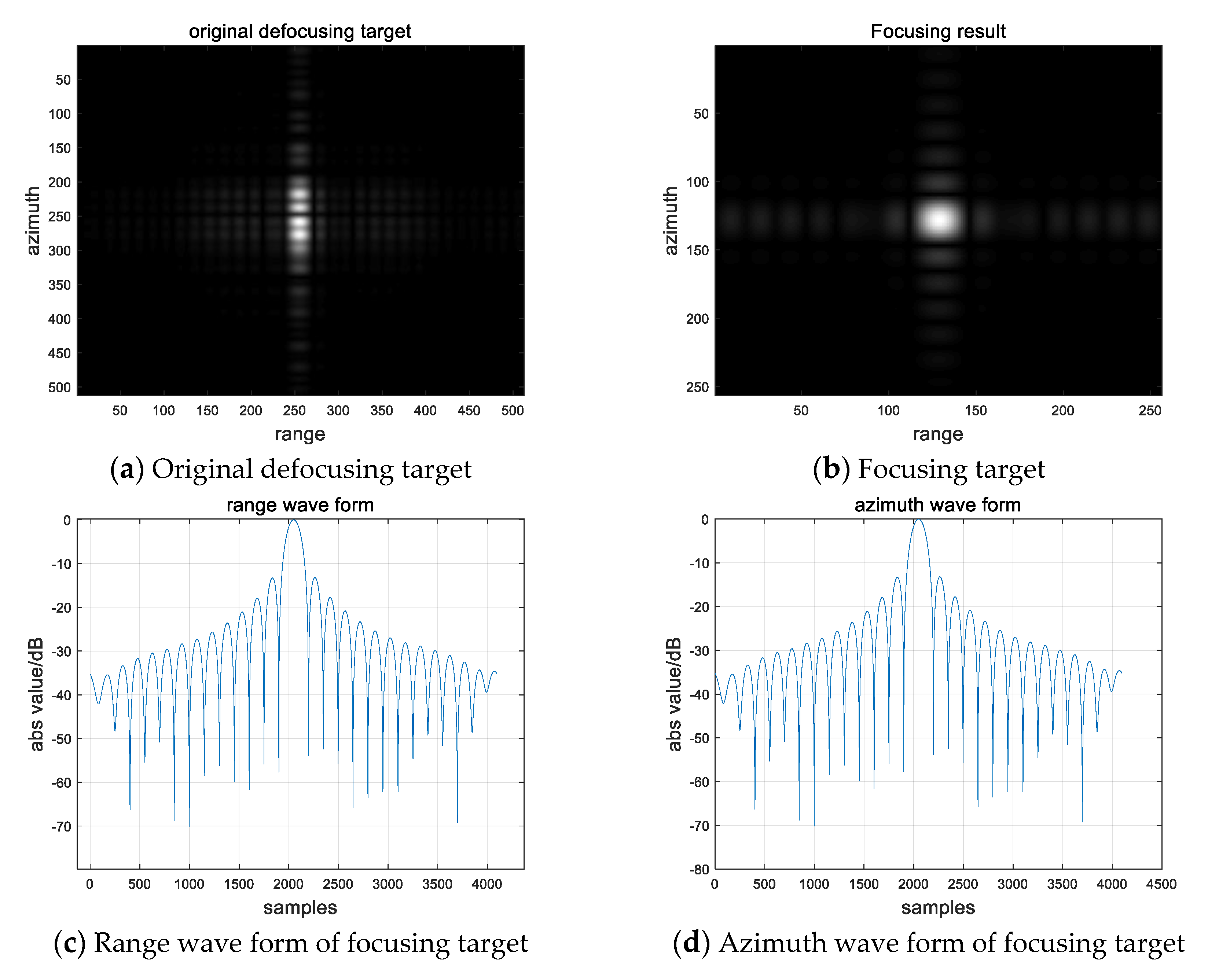
4.1. Simulation Results and Actual Data of Imaging Signatures of Turning Motion
4.2. Simulation Results and Actual Data Results of Velocity Estimation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Herrmann, J.; Bottero, A.G. TerraSAR-X Mission: The new generation in high resolution satellites. In Proceedings of the Anais XIII Simpósio Brasileiro de Sensoriamento Remoto, Florianópolis, Brasil, 21–26 April 2007; pp. 7063–7070. [Google Scholar]
- Zhang, Y.; Gu, X.; Dong, X.; Zhai, W.; Kang, X.; Tang, Y. A Ka-band high-resolution radar system and ground moving target imaging experiment. In Proceedings of the 2015 IEEE International Conference on Microwaves, Communications, Antennas and Electronic Systems (COMCAS), Tel Aviv, Israel, 2–4 November 2015; pp. 1–4. [Google Scholar]
- Tingting, J.; Xiaolan, Q.; Donghui, H.; Ding, C. An ML-Based Radial Velocity Estimation Algorithm for Moving Targets in Spaceborne High-Resolution and Wide-Swath SAR Systems. Remote Sens. 2017, 9, 404–406. [Google Scholar]
- Raney, R.K. Synthetic aperture imaging radar and moving targets. IEEE Trans. Aerosp. Electron. Syst. 1971, 7, 499–505. [Google Scholar] [CrossRef]
- Hongyin, S.; Xiuhua, G.; Zhitao, H.; Zhou, Y. Study on the signature of ground moving target for airborne quint SAR imaging. J. Electron. (China) 2012, 29, 477–484. [Google Scholar]
- Yang, L.; Bi, G.; Xing, M.; Zhang, L. Airborne SAR Moving Target Signatures and Imagery Based on LVD. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5958–5971. [Google Scholar] [CrossRef]
- Yang, Z.; Daping, B.; Aiguo, V.S.; Mingxing, F. Quantitative analysis of the influence of moving target on SAR imaging. Electron. Opt. Control 2017, 4, 19–22. [Google Scholar]
- Pastina, D. Rotation motion estimation for high resolution ISAR and hybrid SAR/ISAR target imaging. In Proceedings of the Radar Conference, Rome, Italy, 26–30 May 2008. [Google Scholar]
- Lazarov, A.D.; Minchev, C.N. SAR Imaging of a Moving Target. In Proceedings of the International Conference on Recent Advances in Space Technologies, Istanbul, Turkey, 14–16 June 2007. [Google Scholar]
- Liu, M.; Wang, P.; Wang, Z. 3D velocity estimation based on FrFT for multi-static SAR. Electron. Lett. 2016, 52, 1565–1567. [Google Scholar] [CrossRef]
- Anghel, A.; Vasile, G.; Ioana, C.; Cacoveanu, R.; Ciochina, S. Vibration estimation in SAR images using azimuth time-frequency tracking and a matched signal transform. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015. [Google Scholar]
- Cai, Y.; Zhong, J. SAR Imaging Simulation for Three-Dimensional Rotations of Ship Targets. Comput. Simul. 2011, 28, 287–291. [Google Scholar]
- Zhang, S.; Sun, G.; Xing, M. Analysis of the SNR for 3-D Rotating Sea Ship Detecting in Geosynchronous Synthetic Aperture Radar System. J. Electron. Inf. Technol. 2016, 038, 1261–1265. [Google Scholar]
- Deng, B.; Wu, C.; Qin, Y.; Li, X.; Wang, H. Advances in Synthetic Aperture Radar Micro-Motion Target Indication(SAR/MMTI). Chin. J. Electron. 2013, 41, 2436–2442. [Google Scholar]
- Yang, J. SAR Ground Moving Target Indication and Imaging Theory. In Study on Ground Moving Target Indication and Imaging Technique of Airborne SAR; Springer: Singapore, 2017. [Google Scholar]
- Zhang, W.; Tong C, M.; Zhang, Q.; Luo, Y.; Zhu, F. Micro-Doppler extraction of ground vibrating targets based on SAR/DPCA technique. XI Tong Gong Cheng Yu Dian Zi Ji Shu/Systems Eng. Electron. 2011, 33, 738–741. [Google Scholar]
- Dawidowicz, B.; Kulpa, K.S.; Misiurewicz, J. Detection of slow moving targets in SAR images using STAP processing with two-channel sigma-delta antenna. In Proceedings of the Radar Conference, Paris, France, 3–4 October 2005. [Google Scholar]
- Lopez-Dekker, P.; Rodriguez-Cassola, M.; Prats, P.; De Zan, F.; Kraus, T.; Sauer, S.; Mittermayer, J. Experimental Bidirectional SAR ATI acquisitions of the ocean surface with TanDEM-X. In Proceedings of the European Conference on Synthetic Aperture Radar (EUSAR), Berlin, Germany, 3–5 June 2014. [Google Scholar]
- Gao, G.; Wang, X.; Lai, T. Detection of Moving Ships Based on a Combination of Magnitude and Phase in along-Track Interferometric SAR—Part II: Statistical Modeling and CFAR Detection. IEEE Trans. Geosci. Remote Sens. 2015, 53, 3582–3599. [Google Scholar] [CrossRef]
- Pappas, O.A.; Achim, A.M.; Bull, D.R. Superpixel-guided CFAR detection of ships at sea in SAR imagery. In Proceedings of the ICASSP 2017—2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Ai, J.; Qi, X.; Yu, W.; Deng, Y.; Liu, F.; Shi, L. A New CFAR Ship Detection Algorithm Based on 2-D Joint Log-Normal Distribution in SAR Images. IEEE Geosci. Remote Sens. Lett. 2010, 7, 806–810. [Google Scholar] [CrossRef]
- Liu, Y.; Cui, H.Y.; Kuang, Z.; Li, G.Q. Ship Detection and Classification on Optical Remote Sensing Images Using Deep Learning. Itm Web Conf. 2017, 12, 05012. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Qu, C.; Shao, J. Ship detection in SAR images based on an improved faster R-CNN. In Proceedings of the 2017 SAR in Big Data Era: Models, Methods and Applications (BIGSARDATA), Beijing, China, 13–14 November 2017. [Google Scholar]
- Liu, L.; Chen, G.; Pan, Z.; Lei, B.; An, Q. Inshore Ship Detection in Sar Images Based on Deep Neural Networks. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar]
- Wang, R.; Li, J.; Duan, Y.; Cao, H.; Zhao, Y. Study on the Combined Application of CFAR and Deep Learning in Ship Detection. J. Indian Soc. Remote Sens. 2018, 46, 1413–1421. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Wu, R.; Xing, M.; Bao, Z. Approach for single channel SAR ground moving target imaging and motion parameter estimation. Iet Radar Sonar Navig. 2007, 1, 1. [Google Scholar] [CrossRef]
- Li, Z.; Wu, J.; Huang, Y.; Yang, H.; Yang, J. Nonsearching Doppler parameter and velocity estimation method for synthetic aperture radar ground moving target imaging. J. Appl. Remote Sens. 2016, 10, 035006. [Google Scholar] [CrossRef]
- Zuo, Y.; Xu, J.; Peng, Y.N.; Xia, X. Parameter estimation for SAR moving target in complex image domain. Sci. China (Information Sciences) 2010, 53, 854–866. [Google Scholar] [CrossRef]
- Hinz, S.; Meyer, F.; Laika, A.; Bamler, R. Spaceborne traffic monitoring with Dual Channel Synthetic Aperture Radar—Theory and Experiments. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05)—Workshops, San Diego, CA, USA, 21–23 June 2005; pp. 20–26. [Google Scholar]
- John, C.C.; Robert, N.M. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: Hoboken, NJ, USA, 1991. [Google Scholar]
- Thayaparan, T. Micro-Doppler Analysis of the Rotation Antenna in Airborne SAR Image Collected by the Apy-6 Radar; IRS: Washington, DC, USA, 2005. [Google Scholar]
- Qun, Z.; Chuangming, T.; Wei, Z. Micro Doppler extraction of ground vibration target based on DPCA clutter suppression. Syst. Eng. Electron. Technol. 2001, 33, 738–741. [Google Scholar]
- Khwaja, A.S.; Zhang, X.P. Motion Parameter Estimation and Focusing from SAR Images Based on Sparse Reconstruction. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1350–1354. [Google Scholar] [CrossRef]
- Zhu, S.; Mohammad-Djafari, A.; Wang, H.; Deng, B.; Li, X.; Mao, J. Parameter estimation for SAR micromotion target based on sparse signal representation. EURASIP. Adv. Signal Process. 2012, 1, 13. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhao, W.; Li, G.; Zhang, Q. Parametric sparse representation method for parameter estimation in SAR imaging. In Proceedings of the International Radar Conference, Hangzhou, China, 14–16 October 2015. [Google Scholar]
- Martorella, M.; Berizzi, F.; Pastina, D.; Lombardo, P. Maritime non-cooperative target imaging with COSMO SkyMed data. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 3564–3567. [Google Scholar]
- Martorella, M.; Giusti, E.; Berizzi, F.; Bacci, A.; Dalle Mese, E. An ISAR technique for refocusing moving targets in SAR images. In Signal and Image Processing for Remote Sensing, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Wang, J.; Liu, X.; Zhou, Z. Minimum-entropy phase adjustment for ISAR. IEE Proc. Radar Sonar Navig. 2004, 151, 203–209. [Google Scholar] [CrossRef]



| Rl | β | θ1 | θ2 |
|---|---|---|---|
| 988.6375 m | 30.3° | −82.8° | −52.5° |
| Parameters | Value | parameters | value |
|---|---|---|---|
| λ | 0.03125 | PRF | 3205.128 |
| Transmit Band | 110 MHz | Lookangle | 42.41° |
| Sample Rate | 120 MHz | Vst | 7368.9706 m/s |
| Reference Range | 577368.962661 | Vg | 7046.7001 m/s |
| Aperture Time | 0.538357 s | fr | 4845.9846 |
| ρa | 3 m | ρr | 1.25 m |
| Dimension | Resolution | PLSR | ILSR |
|---|---|---|---|
| range | 1.182 m | −13.882 dB | −9.998 dB |
| azimuth | 2.212 m | −13.052 dB | −10.035 dB |
| V | Pos Shift | Vy | Vx | Arctan(Vx/Vy) | Vm |
|---|---|---|---|---|---|
| V = 20 km/h | 217.6585 m | 3.4653 m/s | 4.6258 m/s | 53.1618° | 20.807 km/h |
| V = 45 km/h | 505.6712 m | 8.0508 m/s | 9.7932 m/s | 50.5769° | 45.639 km/h |
| V = 65 km/h | 743.1169 m | 11.8312 m/s | 13.8527 m/s | 49.5000° | 65.582 km/h |
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| λ | 0.055517 | PRF | 3566.333984 |
| Transmit Band | 82.5 MHz | Lookangle | 57.61° |
| Sample Rate | 90 MHz | Vst | 7662.5171 m/s |
| Reference Range | 651926.425839 | Vg | 7094.4612 m/s |
| Aperture Time | 0.4684 s | fr | 5337.0810 |
| Items | Estimate Results |
|---|---|
| azimuth shift | 499.9642 m |
| Vy | 12.3641 m/s |
| Vx | 14.2399 m/s |
| Arctan(Vx/Vy) | 49.0331° |
| Vm(m/s) | 18.8586 m/s |
| Vm(km/h) | 67.891 km/h |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, X.; Qiu, X. Research on Turning Motion Targets and Velocity Estimation in High Resolution Spaceborne SAR. Sensors 2020, 20, 2201. https://doi.org/10.3390/s20082201
Wen X, Qiu X. Research on Turning Motion Targets and Velocity Estimation in High Resolution Spaceborne SAR. Sensors. 2020; 20(8):2201. https://doi.org/10.3390/s20082201
Chicago/Turabian StyleWen, Xuejiao, and Xiaolan Qiu. 2020. "Research on Turning Motion Targets and Velocity Estimation in High Resolution Spaceborne SAR" Sensors 20, no. 8: 2201. https://doi.org/10.3390/s20082201
APA StyleWen, X., & Qiu, X. (2020). Research on Turning Motion Targets and Velocity Estimation in High Resolution Spaceborne SAR. Sensors, 20(8), 2201. https://doi.org/10.3390/s20082201





