Non-Contact Water Level Response Measurement of a Tubular Level Gauge Using Image Signals
Abstract
:1. Introduction
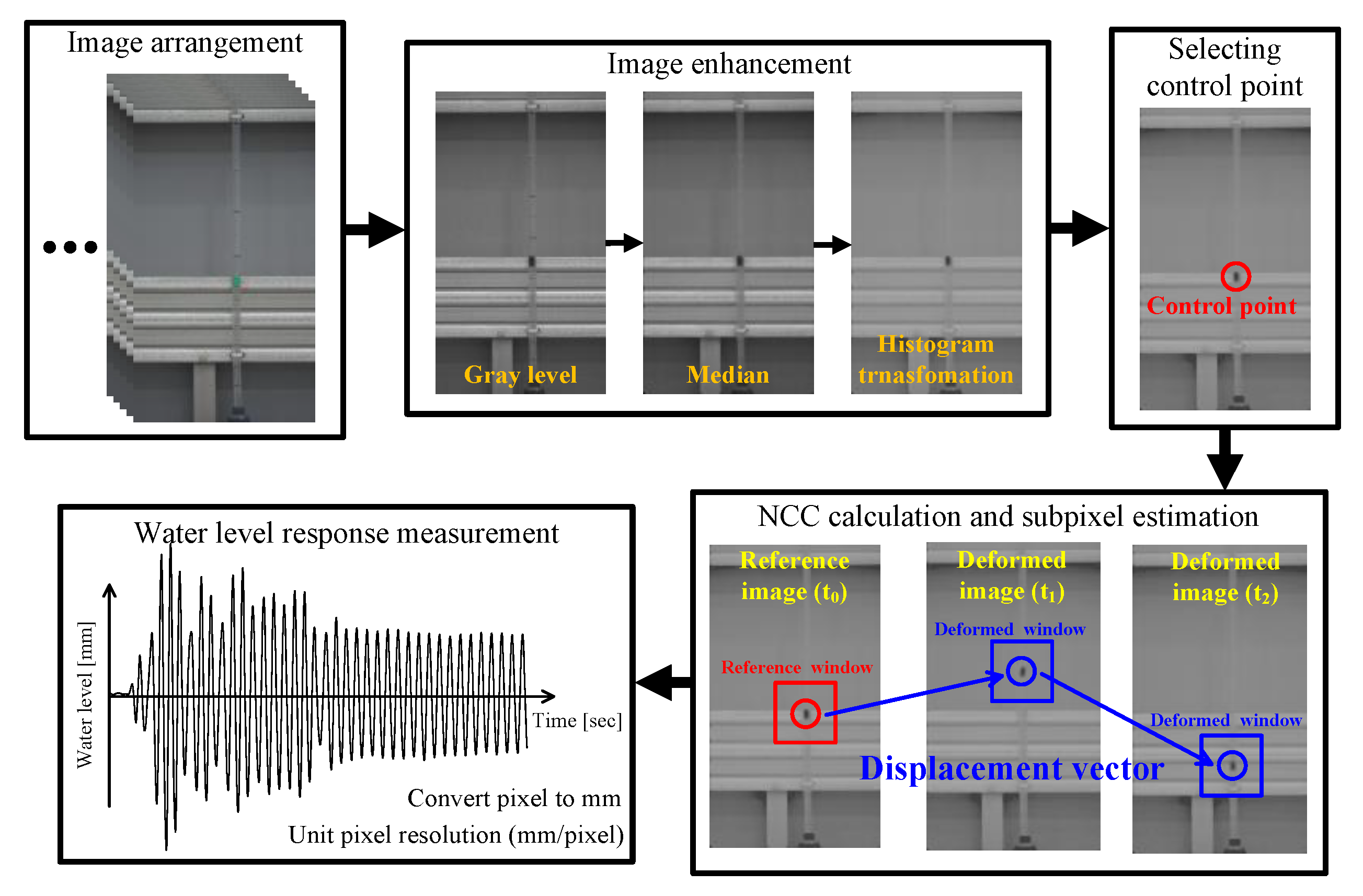
2. Water Level Response Measurement Using Image Signals
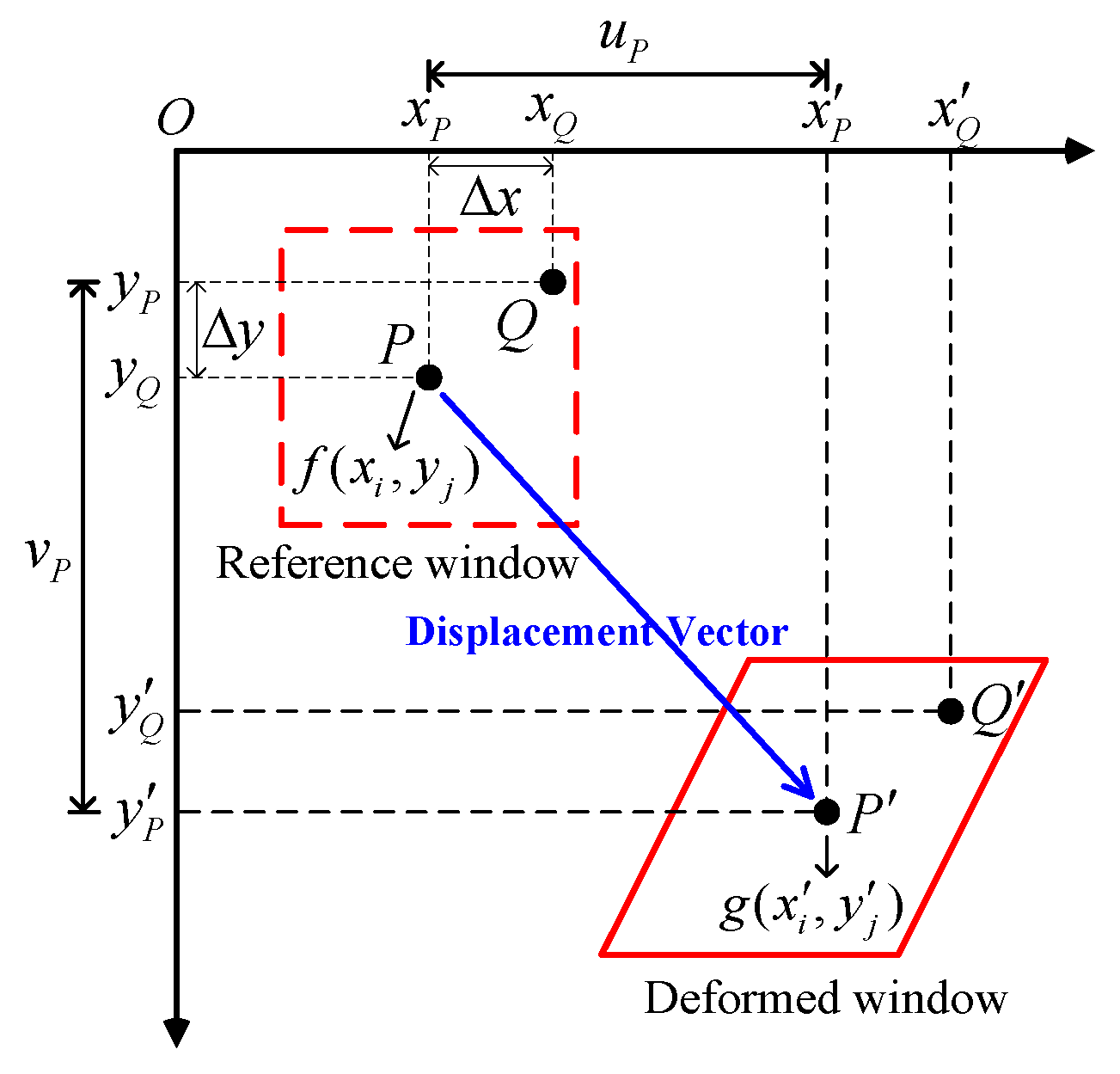
2.1. Image Correlation Method
2.2. Image Enhancement
2.3. Algorithm Summary
3. Estimation of the Water Level Response of the Tubular Level Gauge
3.1. Experiment Setup
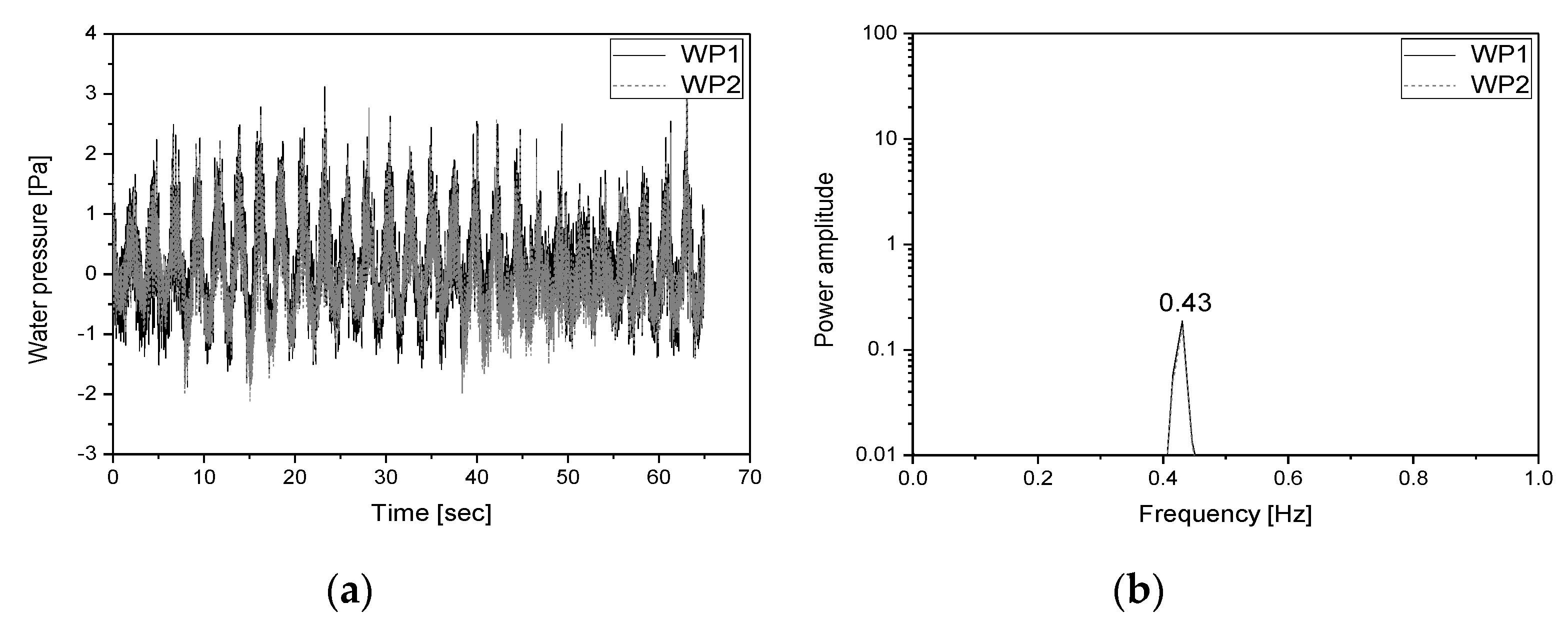
3.2. Dynamic Characteristics of the Liquid Storage Tank
3.3. Application of Image Enhancement Method
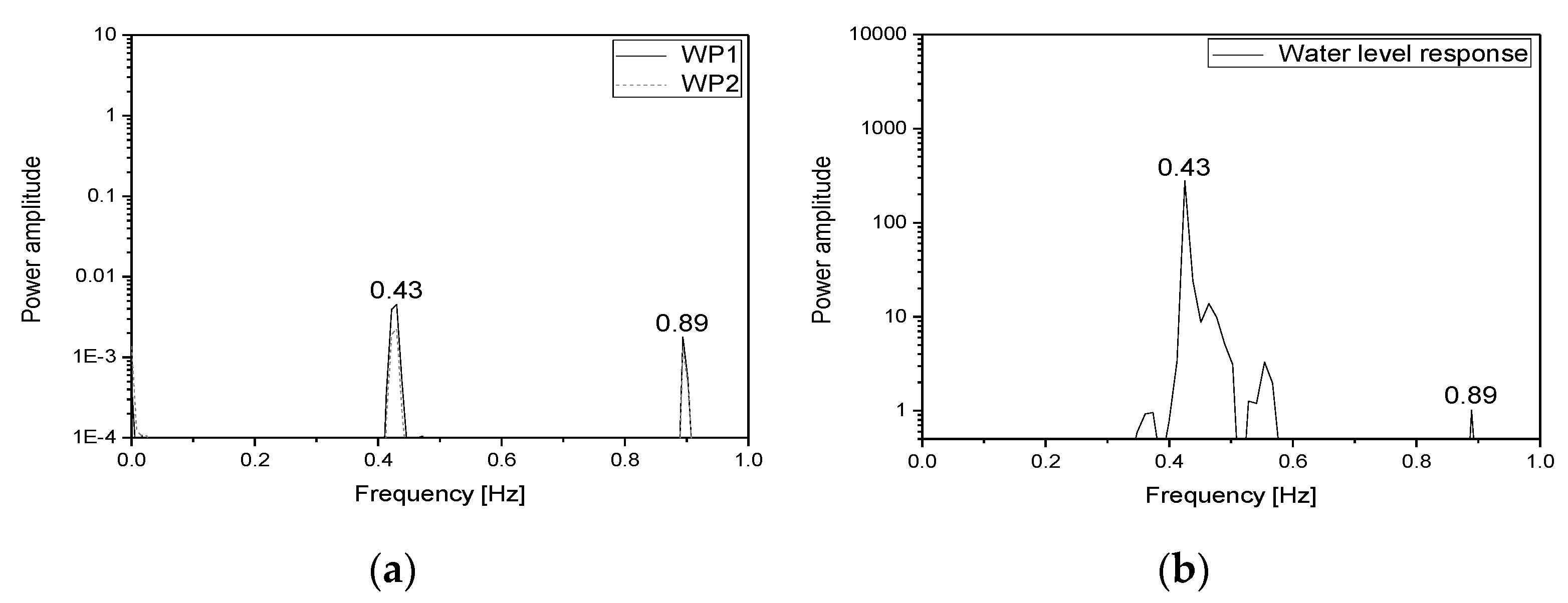
3.4. Water Level Response Measurement in the Shaking Table Test
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chang, J.I.; Lin, C.C. A study of storage tank accidents. J. Loss Prev. Process Ind. 2006, 19, 51–59. [Google Scholar] [CrossRef]
- Sweedan, A.M.I.; El Damatty, A.A. Experimental identification of the vibration modes of liquid-filled conical tanks and validation of a numerical model. Earthq. Eng. Struct. Dyn. 2003, 32, 1407–1430. [Google Scholar] [CrossRef]
- Amiri, M.; Sabbagh-Yazdi, S.R. Influence of roof on dynamic characteristics of dome roof tanks partially filled with liquid. Thin-Walled Struct. 2012, 50, 56–67. [Google Scholar] [CrossRef]
- Virella, J.C.; Godoy, L.A.; Suárez, L.E. Fundamental modes of tank-liquid systems under horizontal motions. Eng. Struct. 2006, 28, 1450–1461. [Google Scholar] [CrossRef]
- Curadelli, O.; Ambrosini, D.; Mirasso, A.; Amani, M. Resonant frequencies in an elevated spherical container partially filled with water: FEM and measurement. J. Fluids Struct. 2010, 26, 148–159. [Google Scholar] [CrossRef]
- Hatayama, K. Lessons from the 2003 Tokachi-oki, Japan, earthquake for prediction of long-period strong ground motions and sloshing damage to oil storage tanks. J. Seismol. 2008, 12, 255–263. [Google Scholar] [CrossRef]
- Isaacson, M.; Premasiri, S. Hydrodynamic damping due to baffles in a rectangular tank. Can. J. Civ. Eng. 2001, 28, 608–616. [Google Scholar] [CrossRef]
- Akyildız, H.; Erdem Ünal, N. Sloshing in a three-dimensional rectangular tank: Numerical simulation and experimental validation. Ocean Eng. 2006, 33, 2135–2149. [Google Scholar] [CrossRef]
- Maleki, A.; Ziyaeifar, M. Sloshing damping in cylindrical liquid storage tanks with baffles. J. Sound Vib. 2008, 311, 372–385. [Google Scholar] [CrossRef]
- Jaiswal, O.R.; Kulkami, S.; Pathak, P. A study on sloshing frequencies of fluid-tank system. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Kolukula, S.S.; Sajish, S.D.; Chellapandi, P. Experimental investigation of slosh parametric instability in liquid filled vessel under seismic excitations. Ann. Nucl. Energy 2015, 76, 218–225. [Google Scholar] [CrossRef]
- Faltinsen, O.M.; Rognebakke, O.F.; Timokha, A.N. Resonant three-dimensional nonlinear sloshing in a square-base basin. J. Fluid Mech. 2003, 487, 1–42. [Google Scholar] [CrossRef] [Green Version]
- Goudarzi, M.A.; Sabbagh-Yazdi, S.R.; Marx, W. Investigation of sloshing damping in baffled rectangular tanks subjected to the dynamic excitation. Bull. Earthq. Eng. 2010, 8, 1055–1072. [Google Scholar] [CrossRef]
- Gao, M. Numerical Simulation of Liquid Sloshing in Rectangular Tanks Using Consistent Particle Method and Experimental Verification. Ph.D. Thesis, National University of Singapore, Singapore, 2011. [Google Scholar]
- Loizou, K.; Koutroulis, E.; Zalikas, D.; Liontas, G. A low-cost capacitive sensor for water level monitoring in large-scale storage tanks. In Proceedings of the IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 1416–1421. [Google Scholar]
- Yan, F.; Shao, X.; Li, G.; Sun, Z.; Yang, Z. Edge detection of tank level IR imaging based on the auto-adaptive double-threshold Canny operator. In Proceedings of the Second International Symposium on Intelligent Information Technology Application, Shanghai, China, 21–22 December 2008; pp. 366–370. [Google Scholar]
- Wnag, C.C.; Chen, P.C.; Liao, C.Y. Application of CCD cameras as a versatile measurement tool for flume tank. Ocean Eng. 2012, 42, 71–82. [Google Scholar] [CrossRef]
- Sangsari, M.K.; Hosseinzadeh, N. Shake table study of impulsive and convective damping coefficients for steel cylindrical tanks and comparison with API 650. J. Seismol. Earthq. Eng. 2014, 16, 129–137. [Google Scholar]
- Hosseinzadeh, N.; Kaypour Sangsari, M.; Tavakolian Ferdosiyeh, H. Shake table study of annular baffles in steel storage tanks as sloshing dependent variable dampers. J. Loss Prev. Process Ind. 2014, 32, 299–310. [Google Scholar] [CrossRef]
- Chien, C.H.; Su, T.H.; Huang, C.J.; Chao, Y.J.; Yeh, W.L.; Lam, P.S. Application of digital image correlation (DIC) to sloshing liquids. Opt. Lasers Eng. 2019, 115, 42–52. [Google Scholar] [CrossRef]
- Tosun, U.; Aghazadeh, R.; Sert, C.; Özer, M.B. Tracking free surface and estimating sloshing force using image processing. Exp. Therm. Fluid Sci. 2017, 88, 423–433. [Google Scholar] [CrossRef]
- Maekawa, K.; Takeda, M.; Hamaura, T.; Suzuki, K.; Matsuno, Y.; Fujikawa, S.; Kumakura, H. Dynamic level-detecting characteristics of external-heating-type MgB2 liquid hydrogen level sensors under liquid level oscillation and its application to sloshing measurement. IEEE Trans. Appl. Supercond. 2017, 27, 7792351. [Google Scholar] [CrossRef]
- Kim, S.W.; Choi, H.S.; Park, D.U.; Baek, E.R.; Kim, J.M. Water level response measurement in a steel cylindrical liquid storage tank using image filter processing under seismic excitation. Mech. Syst. Signal Process. 2018, 101, 274–291. [Google Scholar] [CrossRef]
- Eswaran, M.; Singh, A.; Saha, U.K. Experimental measurement of the surface velocity field in an externally induced sloshing tank. Proc. Inst. Mech. Eng. Part M J. Eng. Marit. Environ. 2011, 225, 133–148. [Google Scholar] [CrossRef]
- Tosun, U.; Aghazadeh, R.; Özer, M.B. Investigating the sloshing characteristics of a liquid using an image processing method. In Proceedings of the 17th International Conference on Fluid Mechanics and Applications (ICFMA), Paris, France, 20–21 July 2015. [Google Scholar]
- Bomarito, G.F.; Hochhalter, J.D.; Ruggles, T.J.; Cannon, A.H. Increasing accuracy and precision of digital image correlation through pattern optimization. Opt. Lasers Eng. 2017, 91, 73–85. [Google Scholar] [CrossRef]
- Pan, B. Digital image correlation for surface deformation measurement: Historical developments, recent advances and future goals. Meas. Sci. Technol. 2018, 29, 082001. [Google Scholar] [CrossRef]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 062001. [Google Scholar] [CrossRef]
- Wang, Z.; Kieu, H.; Nguyen, H.; Le, M. Digital image correlation in experimental mechanics and image registration in computer vision: Similarities, differences and complements. Opt. Lasers Eng. 2015, 65, 18–27. [Google Scholar] [CrossRef]
- Lu, H.; Cary, P.D. Deformation measurements by digital image correlation: Implementation of a second-order displacement gradient. Exp. Mech. 2000, 40, 393–400. [Google Scholar] [CrossRef]
- Kim, S.W.; Choi, H.S.; Jeon, B.G.; Hahm, D.G.; Kim, M.K. Strain and deformation angle for a steel pipe elbow using image measurement system under in-plane cyclic loading. Nucl. Eng. Technol. 2018, 50, 190–202. [Google Scholar] [CrossRef]
- Kim, S.W.; Choi, H.S.; Jeon, B.G.; Hahm, D.G. Low-cycle fatigue behaviors of the elbow in a nuclear power plant piping system using the moment and deformation angle. Eng. Fail. Anal. 2019, 96, 348–361. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, P.; Gupta, M.; Nagawat, A.K. Performance comparison of median and wiener filter in image de-noising. Int. J. Comput. Appl. 2010, 12, 27–31. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, K. A switching median-mean filter for removal of high-density impulse noise from digital images. Optik 2015, 126, 956–961. [Google Scholar] [CrossRef]
- Kaur, M.; Kaur, J. Survey of contrast enhancement techniques based on histogram equalization. Int. J. Adv. Comput. Sci. Appl. 2013, 2, 137–141. [Google Scholar] [CrossRef] [Green Version]
- Singh, H.; Kumar, A.; Balyan, L.K.; Singh, G.K. Swarm intelligence optimized piecewise gamma corrected histogram equalization for dark image enhancement. Comput. Electr. Eng. 2018, 70, 462–475. [Google Scholar] [CrossRef]
- Agarwal, M.; Mahajan, R. Medical image contrast enhancement using range limited weighted histogram equalization. Procedia Comput. Sci. 2018, 125, 149–156. [Google Scholar] [CrossRef]
- Bagheri, N. Development of a high-resolution aerial remote-sensing system for precision agriculture. Int. J. Remote Sens. 2017, 38, 2053–2065. [Google Scholar] [CrossRef]
- Li, X.; Hu, H.; Zhao, L.; Wang, H.; Yu, Y.; Wu, L.; Liu, T. Polarimetric image recovery method combining histogram stretching for underwater imaging. Sci. Rep. 2018, 8, 12430. [Google Scholar] [CrossRef]
- Rahman, S.; Rahman, M.M.; Abdullah-Al-Wadud, M.; Al-Quaderi, G.D.; Shoyaib, M. An adaptive gamma correction for image enhancement. EURASIP J. Image Video Process. 2016, 35. [Google Scholar] [CrossRef] [Green Version]
- Huang, Z.; Zhang, T.; Li, Q.; Fang, H. Adaptive gamma correction based on cumulative histogram for enhancing near-infrared images. Infrared Phys. Technol. 2016, 79, 205–215. [Google Scholar] [CrossRef]
- Seismic Design of Liquid Containing Concrete Structures ACI 350.3; American Concrete Institute (ACI): Farmington Hills, MI, USA, 2001.
- Kim, S.W.; Lee, S.S.; Kim, N.S.; Kim, D.J. Numerical model validation for a prestressed concrete girder bridge by using image signals. KSCE J. Civ. Eng. 2013, 17, 509–517. [Google Scholar] [CrossRef]








| Filter | Image Filter Processing |
|---|---|
| Filter 1 | Gray level |
| Filter 2 | Median |
| Filter 3 | Histogram transformation |
| Filter 4 | Median + histogram transformation |
| Load Case | Seismic Wave | Direction |
|---|---|---|
| 1 | Random | X |
| 2 | El Centro, 50% | X |
| 3 | El Centro, 100% | X |
| Load Case | Cross Correlation Function | Percent Error (%) | Root Mean Square (RMS) Error (mm) |
|---|---|---|---|
| 1 | 0.988 | 0.427 | 0.162 |
| 2 | 0.983 | 0.359 | 0.141 |
| 3 | 0.979 | 0.545 | 0.258 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.-W.; Park, D.-U.; Jeon, B.-G.; Chang, S.-J. Non-Contact Water Level Response Measurement of a Tubular Level Gauge Using Image Signals. Sensors 2020, 20, 2217. https://doi.org/10.3390/s20082217
Kim S-W, Park D-U, Jeon B-G, Chang S-J. Non-Contact Water Level Response Measurement of a Tubular Level Gauge Using Image Signals. Sensors. 2020; 20(8):2217. https://doi.org/10.3390/s20082217
Chicago/Turabian StyleKim, Sung-Wan, Dong-Uk Park, Bub-Gyu Jeon, and Sung-Jin Chang. 2020. "Non-Contact Water Level Response Measurement of a Tubular Level Gauge Using Image Signals" Sensors 20, no. 8: 2217. https://doi.org/10.3390/s20082217
APA StyleKim, S.-W., Park, D.-U., Jeon, B.-G., & Chang, S.-J. (2020). Non-Contact Water Level Response Measurement of a Tubular Level Gauge Using Image Signals. Sensors, 20(8), 2217. https://doi.org/10.3390/s20082217





