Fault Diagnosis of Wind Turbine Gearbox Based on the Optimized LSTM Neural Network with Cosine Loss
Abstract
:1. Introduction
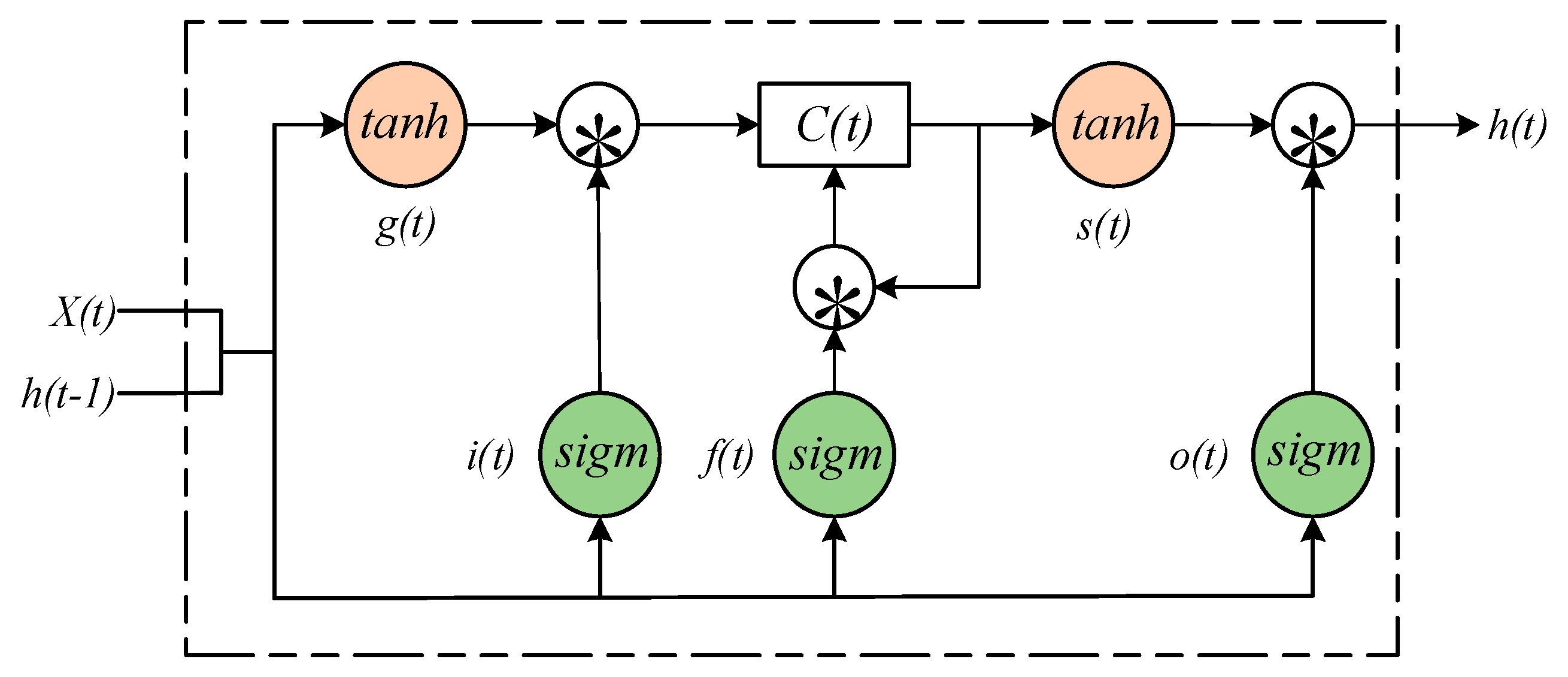
2. LSTM Neural Network for Fault Diagnosis
2.1. Structure of LSTM
- The input gate i(t), which decides whether the information can get in the memory element;
- The forget gate f(t), which decides whether the internal information needs to be forgotten;
- The output gate o(t), which decides what information can pass through the gate and get into the rest of the neural network.
2.2. Architecture of LSTM for Fault Diagnosis
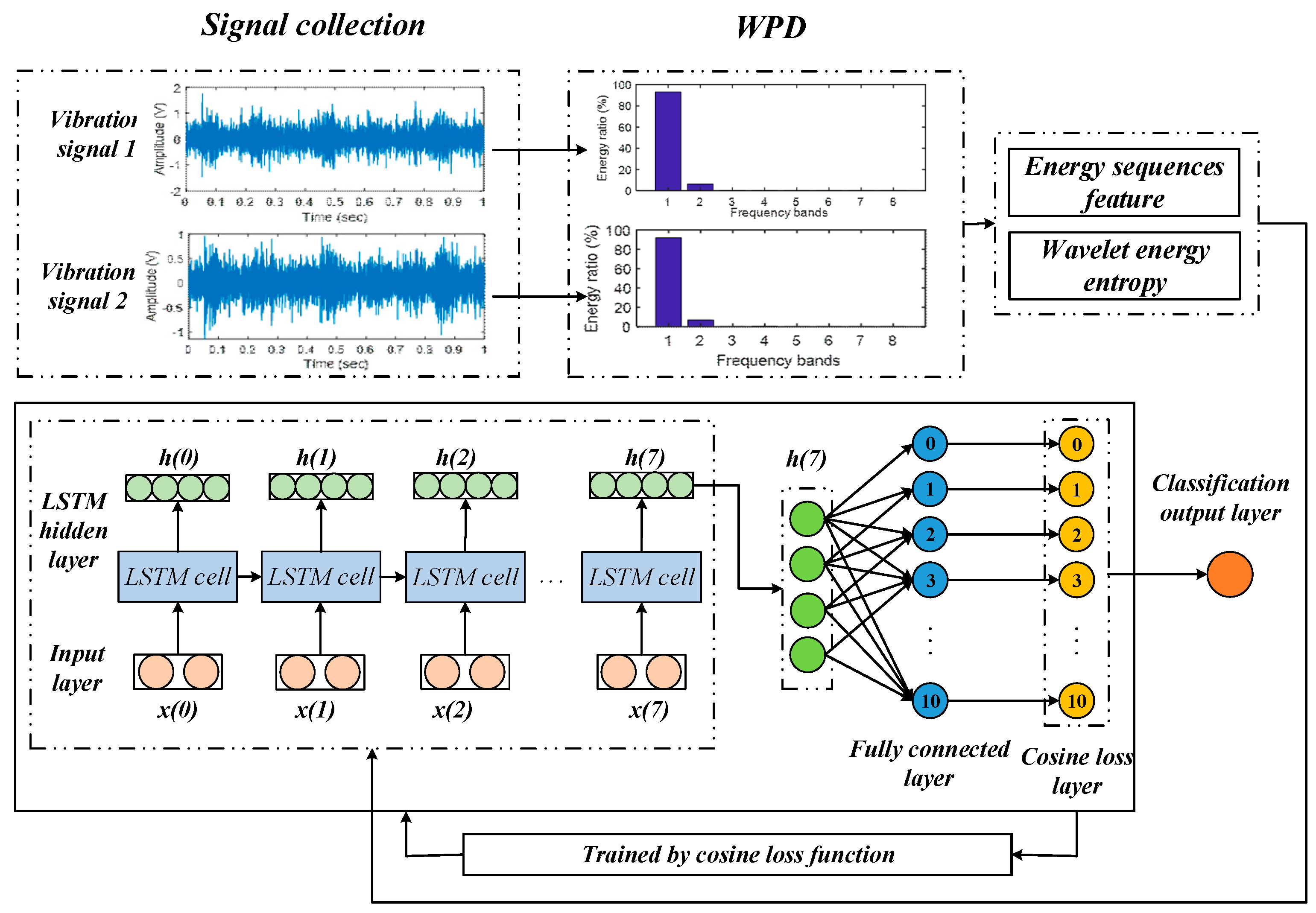
3. Cos-LSTM
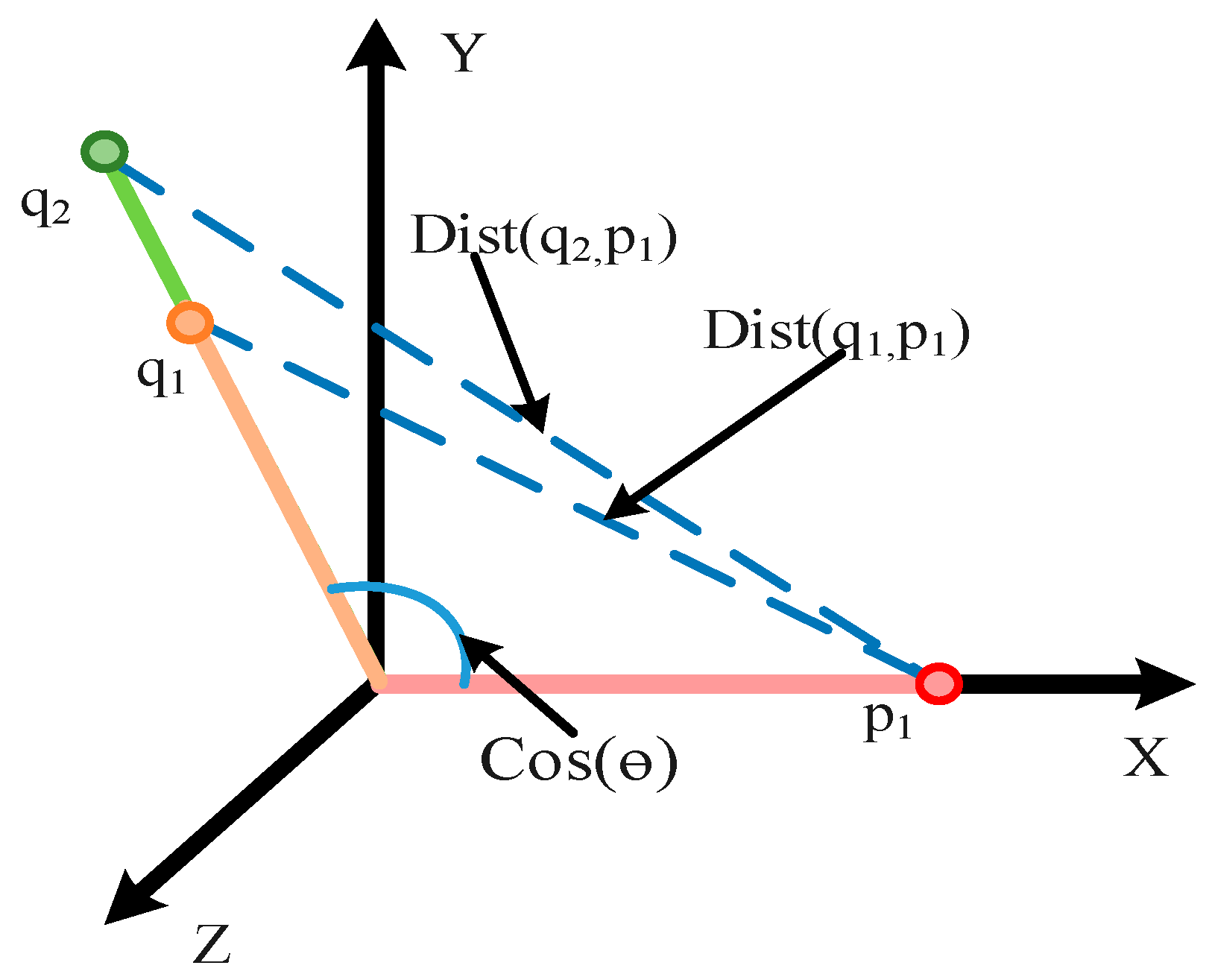
3.1. Cosine Loss
3.2. The Process of Cos-LSTM for Fault Diagnosis
4. Experimental Validation
4.1. Experiment Description
4.2. Experimental Results
4.3. Comparison Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhao, X.; Yan, Z.; Zhang, X.-P. A Wind-Wave Farm System with Self-Energy Storage and Smoothed Power Output. IEEE Access 2016, 4, 8634–8642. [Google Scholar] [CrossRef]
- Hu, A.; Yan, X.; Xiang, L. A new wind turbine fault diagnosis method based on ensemble intrinsic time-scale decomposition and WPT-fractal dimension. Renew. Energy 2015, 83, 767–778. [Google Scholar] [CrossRef]
- Walford, C.A. Wind Turbine Reliability: Understanding and Minimizing Wind Turbine Operation and Maintenance Costs; Sandia National Laboratories: Albuquerque, NM, USA, 2006.
- Jiang, G.; He, H.; Yan, J.; Xie, P. Multiscale Convolutional Neural Networks for Fault Diagnosis of Wind Turbine Gearbox. IEEE Trans. Ind. Electron. 2019, 66, 3196–3207. [Google Scholar] [CrossRef]
- Feng, Z.; Qin, S.; Liang, M. Time-frequency analysis based on Vold-Kalman filter and higher order energy separation for fault diagnosis of wind turbine planetary gearbox under nonstationary conditions. Renew. Energy 2016, 85, 45–56. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, W.; Chu, F. Planet gear fault localization for wind turbine gearbox using acoustic emission signals. Renew. Energy 2017, 109, 449–460. [Google Scholar] [CrossRef]
- Bejger, A.; Chybowski, L.; Gawdzinska, K. Utilising elastic waves of acoustic emission to assess the condition of spray nozzles in a marine diesel engine. J. Mar. Eng. Technol. 2018, 17, 153–159. [Google Scholar] [CrossRef] [Green Version]
- Bejger, A.; Drzewieniecki, J.B. The Use of Acoustic Emission to Diagnosis of Fuel Injection Pumps of Marine Diesel Engines. Energies 2019, 12. [Google Scholar] [CrossRef] [Green Version]
- Jia, F.; Lei, Y.; Lin, J.; Zhou, X.; Lu, N. Deep neural networks: A promising tool for fault characteristic mining and intelligent diagnosis of rotating machinery with massive data. Mech. Syst. Signal Process. 2016, 72–73, 303–315. [Google Scholar] [CrossRef]
- Lei, Y.; Jia, F.; Lin, J.; Xing, S.; Ding, S.X. An Intelligent Fault Diagnosis Method Using Unsupervised Feature Learning Towards Mechanical Big Data. IEEE Trans. Ind. Electron. 2016, 63, 3137–3147. [Google Scholar] [CrossRef]
- Lei, Y.; He, Z.; Zi, Y.; Hu, Q. Fault diagnosis of rotating machinery based on multiple ANFIS combination with GAS. Mech. Syst. Signal Process. 2007, 21, 2280–2294. [Google Scholar] [CrossRef]
- Wang, D.; Tse, P.W.; Guo, W.; Miao, Q. Support vector data description for fusion of multiple health indicators for enhancing gearbox fault diagnosis and prognosis. Meas. Sci. Technol. 2011, 22. [Google Scholar] [CrossRef] [Green Version]
- Gao, Q.W.; Liu, W.Y.; Tang, B.P.; Li, G.J. A novel wind turbine fault diagnosis method based on intergral extension load mean decomposition multiscale entropy and least squares support vector machine. Renew. Energy 2018, 116, 169–175. [Google Scholar] [CrossRef]
- Santos, P.; Villa, L.F.; Renones, A.; Bustillo, A.; Maudes, J. An SVM-Based Solution for Fault Detection in Wind Turbines. Sensors 2015, 15, 5627–5648. [Google Scholar] [CrossRef] [Green Version]
- Abbasion, S.; Rafsanjani, A.; Farshidianfar, A.; Irani, N. Rolling element bearings multi-fault classification based on the wavelet denoising and support vector machine. Mech. Syst. Signal Process. 2007, 21, 2933–2945. [Google Scholar] [CrossRef]
- Liu, W.Y.; Gao, Q.W.; Ye, G.; Ma, R.; Lu, X.N. A novel wind turbine bearing fault diagnosis method based on Integral Extension LMD. Measurement 2015, 74, 70–77. [Google Scholar] [CrossRef]
- Lei, Y. Intelligent Fault Diagnosis and Remaining Useful Life Prediction of Rotating Machinery; Xi’an Jiaotong University Press: Xi’an, China, 2017. [Google Scholar]
- Li, C.; Sanchez, R.-V.; Zurita, G.; Cerrada, M.; Cabrera, D. Fault Diagnosis for Rotating Machinery Using Vibration Measurement Deep Statistical Feature Learning. Sensors 2016, 16. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Li, C.; Sanchez, R.-V. Gearbox Fault Identification and Classification with Convolutional Neural Networks. Shock Vib. 2015. [Google Scholar] [CrossRef] [Green Version]
- An, Z.; Li, S.; Wang, J.; Jiang, X. A novel bearing intelligent fault diagnosis framework under time-varying working conditions using recurrent neural network. ISA Trans. 2019. [Google Scholar] [CrossRef]
- Cao, L.; Zhang, J.; Wang, J.; Qian, Z. Intelligent fault diagnosis of wind turbine gearbox based on Long short-term memory networks. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics, Vancouver, BC, Canada, 12–14 June 2019; pp. 890–895. [Google Scholar]
- Medina, R.; Cerrada, M.; Cabrera, D.; Sanchez, R.-V.; Li, C.; de Oliveira, J.V. Deep Learning-Based Gear Pitting Severity Assessment using Acoustic Emission, Vibration and Currents signals. In Proceedings of the 2019 Prognostics and System Health Management Conference, Paris, France, 2–5 May 2019; pp. 210–216. [Google Scholar]
- Wang, H.; Wang, Y.; Zhou, Z.; Ji, X.; Gong, D.; Zhou, J.; Li, Z.; Liu, W. CosFace: Large Margin Cosine Loss for Deep Face Recognition. In Proceedings of the 2018 IEEE/Cvf Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 5265–5274. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Graves, A. Supervised sequence labelling. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 5–13. [Google Scholar]
- Wen, Y.; Zhang, K.; Li, Z.; Qiao, Y. A discriminative feature learning approach for deep face recognition. Proceedings of European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 499–515. [Google Scholar]
- Liu, W.; Wen, Y.; Yu, Z.; Li, M.; Raj, B.; Song, L. SphereFace: Deep Hypersphere Embedding for Face Recognition. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6738–6746. [Google Scholar]
- Shao, Y.; Ge, L.; Fang, J. Fault diagnosis system based on smart bearing. In Proceedings of the 2008 International Conference on Control, Automation and Systems, Seoul, Korea, 14–17 October 2008; pp. 1084–1089. [Google Scholar]
- Kedadouche, M.; Liu, Z. Fault feature extraction and classification based on WPT and SVD: Application to element bearings with artificially created faults under variable conditions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 4186–4196. [Google Scholar] [CrossRef]
- Wang, D.C.; Ding, Y.F.; Zhu, C.X. A fault diagnosis method for gearbox based on neutrosophic K-Nearest Neighbor. Shock Vib. 2019, 38, 148–153. [Google Scholar] [CrossRef]
- Wang, W.Q.; Yang, S. A method for choosing the wavelet decomposition level in structural fault analysis. Struct. Environ. Eng. 2009. [Google Scholar] [CrossRef]
- Wu, C.Z.; Jiang, P.C.; Feng, F.Z.; Chen, T.; Chen, X.L. Gearbox Faults diagnosis method for gearboxes based on 1-D convolutional neural network. Shock Vib. 2018, 37, 51–56. [Google Scholar] [CrossRef]


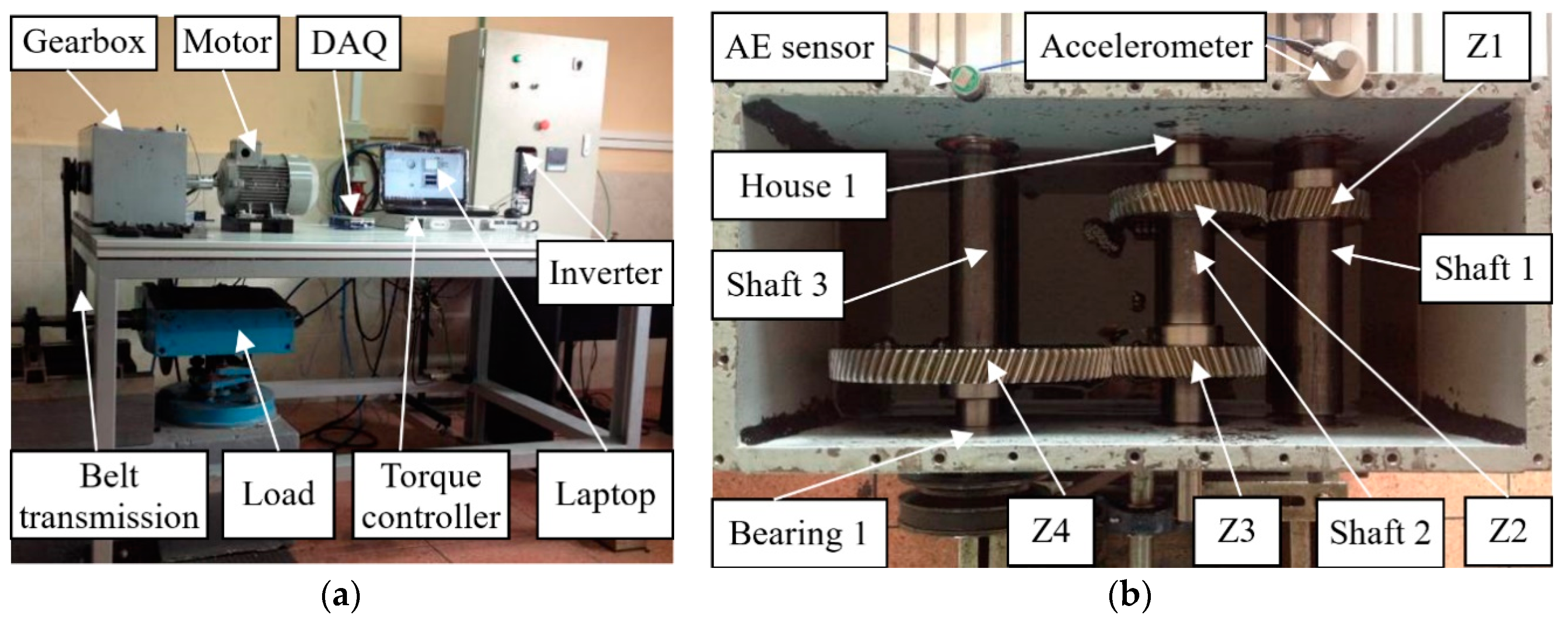


| Item | Parameter |
|---|---|
| Sensor | PCB ICP 353C03 accelerometer |
| Data acquisition box Software | NI cDAQ-9234 LabVIEW |
| Sampling rate | 50 kHz |
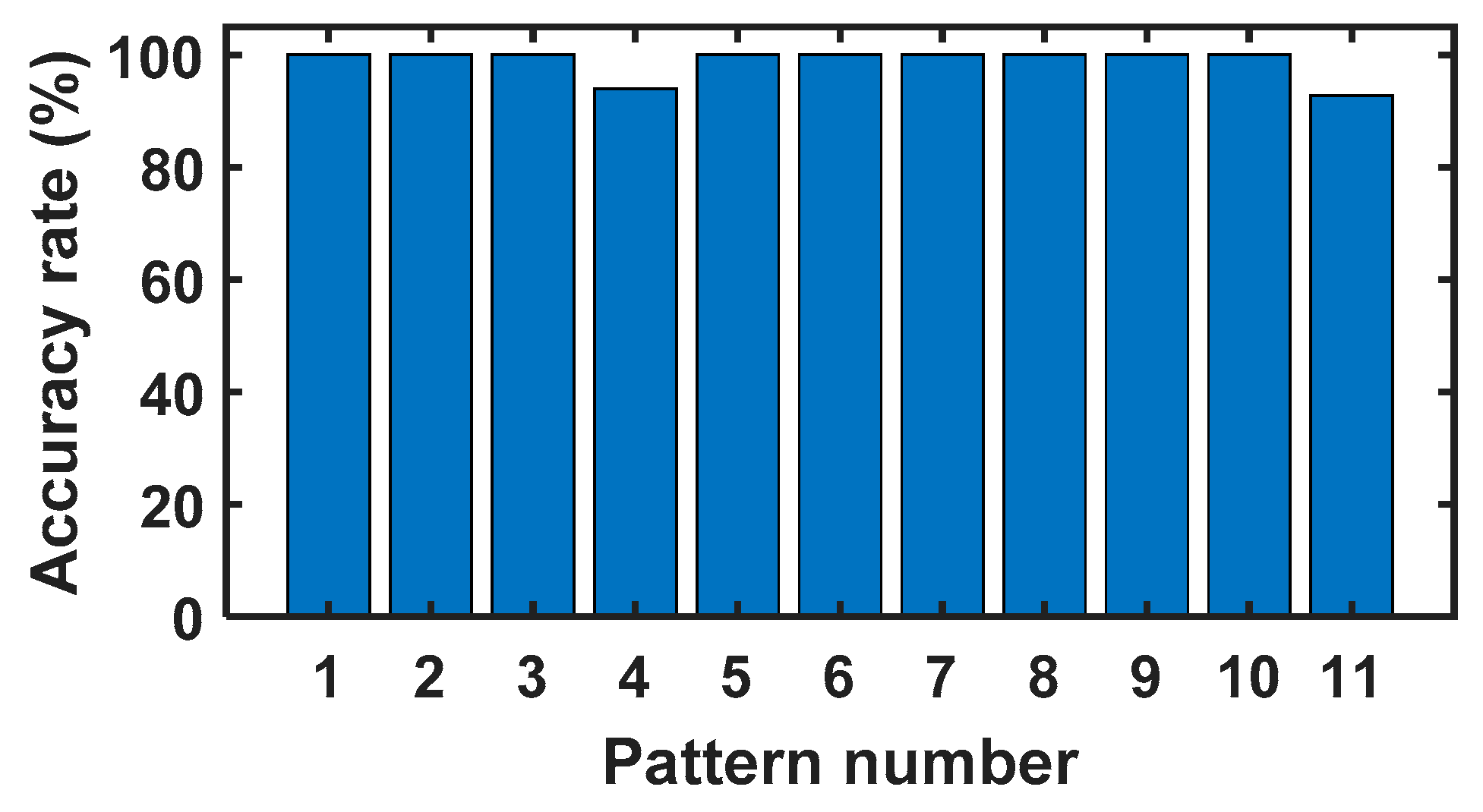
| Pattern Number | Faulty Component | Faulty Name | Input Speed (rpm) | Load (V) | View of the Failure |
|---|---|---|---|---|---|
| 1 | N/A | N/A | 480, 720, 900 | 0, 10, 30 | N/A |
| 2 | Gear Z1 | Worn tooth | 480, 720, 900 | 0, 10, 30 |  |
| 3 | Gear Z2 | Chafing tooth | 480, 720, 900 | 0, 10, 30 |  |
| 4 | Gear Z3 | Pitting tooth | 480, 720, 900 | 0, 10, 30 |  |
| 5 | Gear Z3 | Worn tooth | 480, 720, 900 | 0, 10 30 |  |
| 6 | Gear Z4 | Root crack tooth | 480, 720, 900 | 0, 10, 30 |  |
| 7 | Gear Z4 | Chafing tooth | 480, 720, 900 | 0, 10, 30 |  |
| 8 | Bearing 1 | Inner race fault | 480, 720, 900 | 0, 10, 30 |  |
| 9 | Bearing 1 | Outer race fault | 480, 720, 900 | 0, 10, 30 |  |
| 10 | Bearing 1 | Ball fault | 480, 720, 900 | 0, 10, 30 |  |
| 11 | House 1 | Eccentric | 480, 720, 900 | 0, 10, 30 |  |
| Feature | Fault Diagnosis Methods | Accuracy Rate |
|---|---|---|
| The energy sequence | Cos-LSTM | 98.55% |
| LSTM | 96.72% | |
| SVM | 65.48% | |
| KNN | 83.93% | |
| BP neural network | 69.64% | |
| Wavelet Energy entropy | Cos-LSTM | 98.08% |
| Item | Parameter | Accuracy Rate |
|---|---|---|
| Wavelet basis function | Daubechies 3 | 98.55% |
| Daubechies 2 | 96.36% | |
| Haar | 93.82% | |
| Symlet | 97.09% | |
| Segment size | 2 | 96.63% |
| 3 | 97.12% | |
| 4 | 98.55% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, A.; Yan, Y.; Zhang, Z.; Li, C.; Sánchez, R.-V. Fault Diagnosis of Wind Turbine Gearbox Based on the Optimized LSTM Neural Network with Cosine Loss. Sensors 2020, 20, 2339. https://doi.org/10.3390/s20082339
Yin A, Yan Y, Zhang Z, Li C, Sánchez R-V. Fault Diagnosis of Wind Turbine Gearbox Based on the Optimized LSTM Neural Network with Cosine Loss. Sensors. 2020; 20(8):2339. https://doi.org/10.3390/s20082339
Chicago/Turabian StyleYin, Aijun, Yinghua Yan, Zhiyu Zhang, Chuan Li, and René-Vinicio Sánchez. 2020. "Fault Diagnosis of Wind Turbine Gearbox Based on the Optimized LSTM Neural Network with Cosine Loss" Sensors 20, no. 8: 2339. https://doi.org/10.3390/s20082339







