Safe Helicopter Landing on Unprepared Terrain Using Onboard Interferometric Radar
Abstract
1. Introduction
2. Description of the RSLSH
3. Numerical Simulation
3.1. Structure of the Simulation Model
3.2. Digital Elevation Model
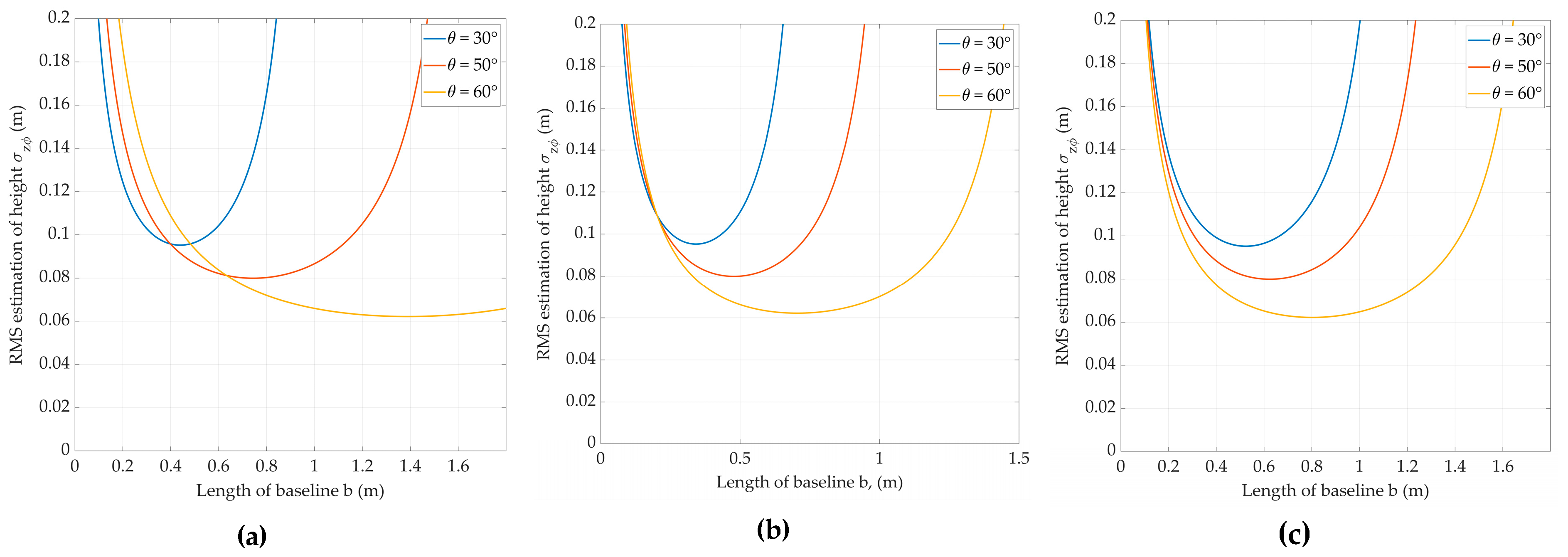
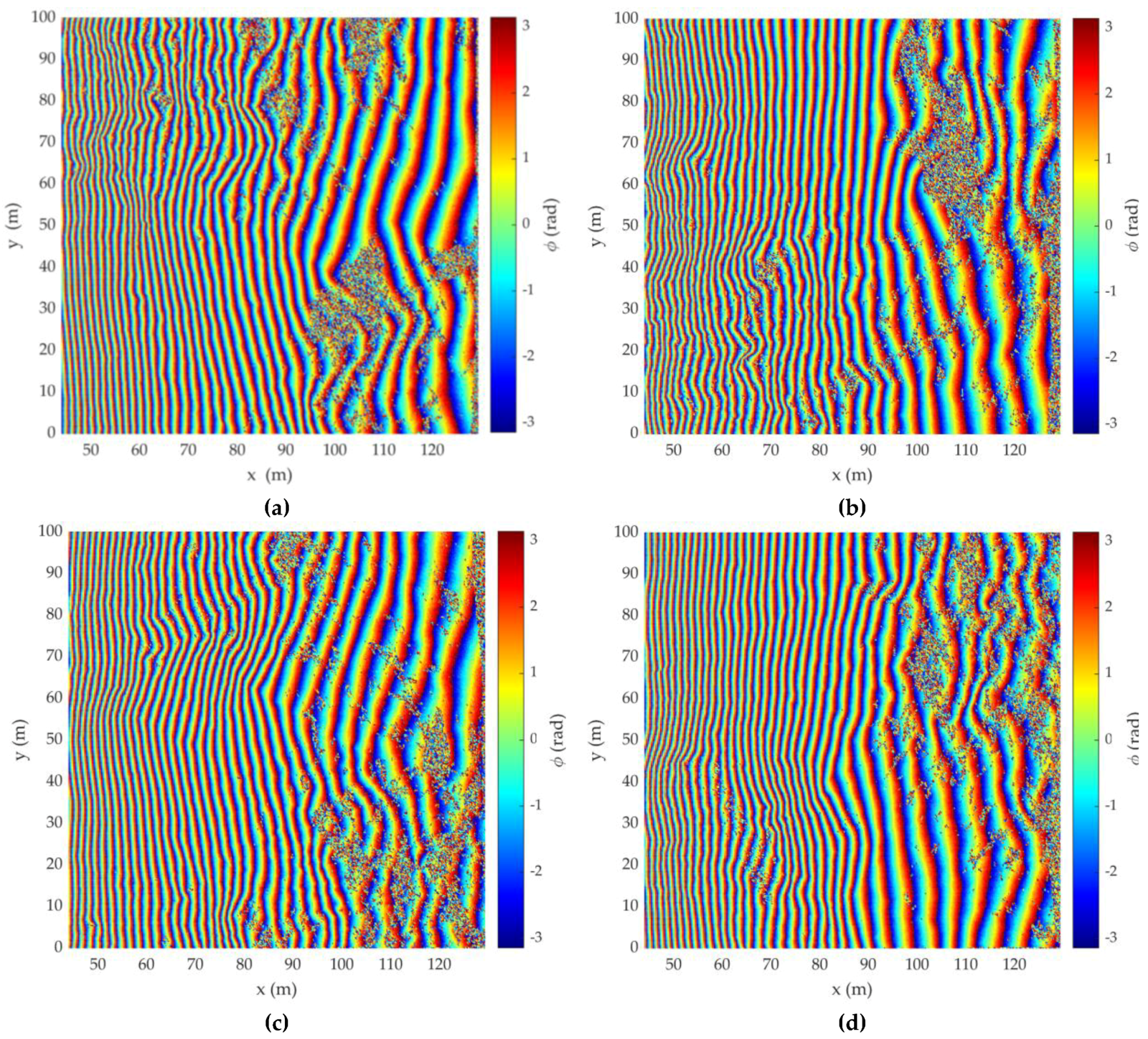
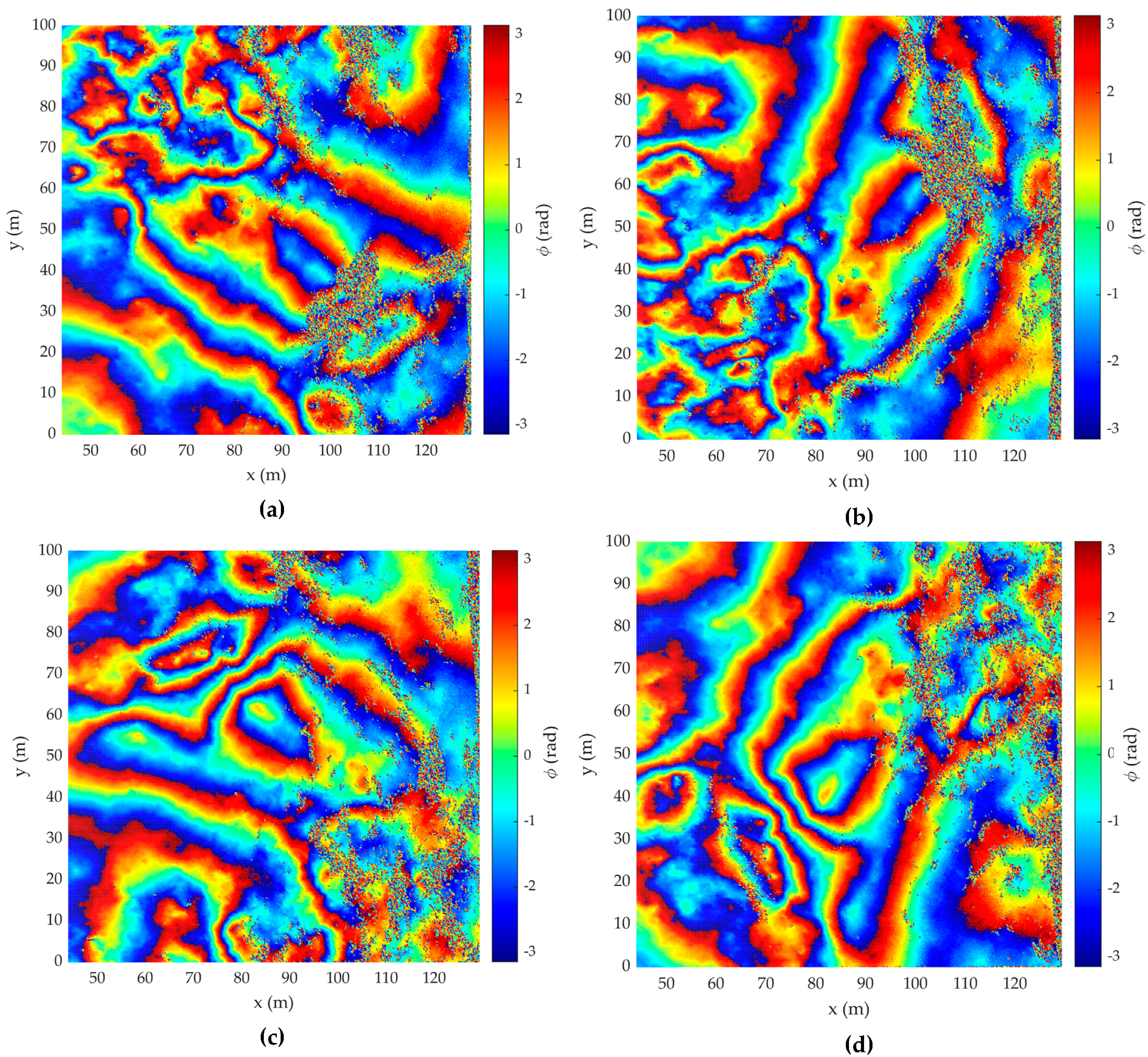
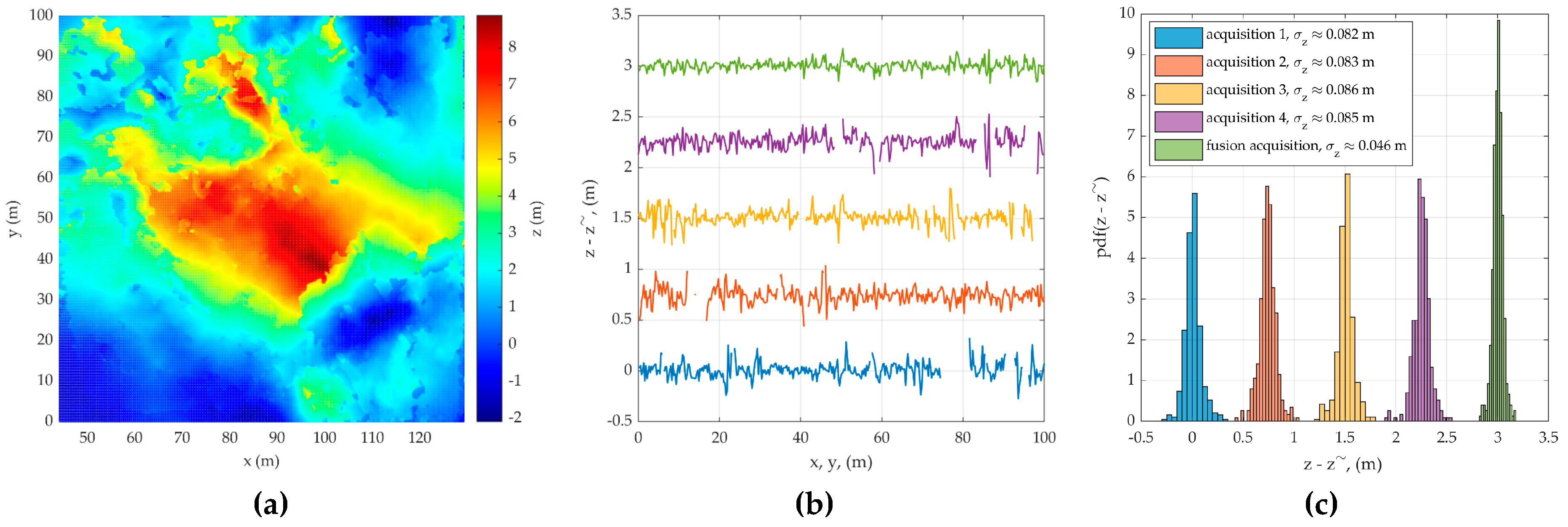
3.3. Synthesis of Radar Images and IPD Processing
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rotary–Wing Brownout Mitigation: Technologies and Training; Technical Report; NATO Science and Technology Organization: Paris, France, 2012.
- Analysis of the State of Flight Safety in the Civil Aviation of the Russian Federation in the First Half of 2016. In Flight Safety Inspectorate; Federal Air Transport Agency of the Russian Federation: Moscow, Russia, 2016.
- Cheung, B.W. Nonvisual Spatial Orientation Mechanisms. Spatial Disorientation in Aviation. Prog. Astronaut. Aeronaut. 2004, 203, 37–94. [Google Scholar] [CrossRef]
- Cross, J.; Schneider, J.; Cariani, P. MMW radar enhanced vision systems: The Helicopter Autonomous Landing System (HALS) and Radar-Enhanced Vision System (REVS) are rotary and fixed wing enhanced flight vision systems that enable safe flight operations in degraded visual environments. In Proceedings of the Degraded Visual Environments: Enhanced, Synthetic, and External Vision Solutions 2014, Baltimore, MD, USA, 7–8 May 2014. [Google Scholar] [CrossRef]
- Sykora, B. BAE systems brownout landing aid system technology (BLAST) system overview and flight test results. In Proceedings of the Airborne Intelligence, Surveillance, Reconnaissance (ISR) Systems and Applications IX, 83600M, Baltimore, MD, USA, 24–26 April 2012. [Google Scholar] [CrossRef]
- Savage, J.; Harrington, W.; McKinley, A.R.; Burns, H.M.; Braddom, S.; Szoboszlay, Z. 3D–LZ helicopter lidar imaging system. In Proceedings of the Laser Radar Technology and Applications XV, Orlando, FL, USA, 5–9 April 2010. [Google Scholar] [CrossRef]
- Murray, J.T.; Seely, J.; Plath, J.; Gotfreson, E.; Engel, J.; Ryder, B.; Van Lieu, N.; Goodwin, R.; Wagner, T.; Fetzer, G.; et al. Dust-Penetrating (DUSPEN) “see-through” lidar for helicopter situational awareness in DVE. In Proceedings of the Degraded Visual Environments: Enhanced, Synthetic, and External Vision Solutions 2013, Baltimore, MA, USA, 16 May 2013. [Google Scholar] [CrossRef]
- Rangwala, J.M.; Srabandi, L.K. Design of FMCW Millimeter-Wave Radar for Helicopter Assisted Landing. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 4183–4186. [Google Scholar] [CrossRef]
- Braun, H.M.; Baessler, H.; Jackson, B.; Jonas, C.; Lentz, H.; Rhein, R.V.; Essen, H. Helicopter Flight and Landing RADAR—A New Technology Developed in the European EUROSTARS Program. In Proceedings of the 2013 14th International Radar Symposium (IRS), Dresden, Germany, 19 June 2013; Volume 1, pp. 1214–1217. [Google Scholar]
- Manual on the flight operation of the Mi-8 helicopter. M.: Air Transport Department of the Ministry of Transport of the Russian Federation.
- Baskakov, A.I.; Jutyaeva, T.S.; Lukashenko, Y.I. Locational Methods for Studying Objects and Environments. A Textbook for University Students; Baskakov, A.I.M., Ed.; Academy: Katy, TX, USA, 2011. [Google Scholar]
- Baskakov, A.I.; Ka, M.-H. Analysis of the Effect of Phase Noise on the Accuracy Characteristics of Interferometric Fixed-Baseline SARs. In Earth Observation and Remote Sensing; Russian Academy of Science: Moscow, Russia, 2000; pp. 247–256. ISBN 1024-5251. [Google Scholar]
- Ka, M.H.; Kononov, A.A. Effect of Look Angle on the Accuracy Performance of Fixed-Baseline Interferometric SAR. IEEE Geosci. Remote Sens. Lett. 2007, 4, 65–69. [Google Scholar] [CrossRef]
- Rodriguez, E.; Martin, J.M. Theory and design of interferometric synthetic aperture radars. IEE Proc. Radar Signal Process. 1992, 139, 147–159. [Google Scholar] [CrossRef]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl. 1998, 14, R1. [Google Scholar] [CrossRef]
- Ka, M.-H.; Shimkin, P.E.; Baskakov, A.I.; Babokin, M.I. A New Single-Pass SAR Interferometry Technique with a Single-Antenna for Terrain Height Measurements. Remote Sens. 2019, 11, 1070. [Google Scholar] [CrossRef]
- Richards, M.A.; Scheer, J.A.; Holm, W.A. Principles of Modern Radar: Basic Principles; SciTech Publishing: Raleigh, NC, USA, 2010; p. 934. [Google Scholar]
- Adib, N.; Fawwz, T.; Kamal, S. Measurement and modeling of the millimeter-wave backscatter response of soil surfaces. IEEE Trans. Geosci. Remote Sens. 1996, 34, 561–572. [Google Scholar]
- Gatesman, A.J.; Goyette, T.M.; Dickinson, J.C.; Waldman, J.; Neilson, J.; Nixon, W.E. Physical Scale Modeling the Millimeter-Wave Backscattering Behavior of Ground Clutter. In Targets and Backgrounds VII: Characterization and Representation; International Society for Optics and Photonics: Bellingham, WA, USA, 2001. [Google Scholar]
- Li, E.S. Millimeter Wave Polarimetric Radar System as an Advanced Vehicle Control and Warning Sensor. Ph. D. Thesis, University of Michigan, Ann Arbor, Michigan, 1998. [Google Scholar]
- Richards, M.A. A beginner’s guide to interferometric SAR concepts and signal processing. IEEE Aerosp. Electron. Syst. Mag. 2007, 22, 5–29. [Google Scholar] [CrossRef]
- Melvin, W.L.; Sheer, J.A. Interferometric SAR and coherent exploitation. In Principles of Modern Radar: Advanced Techniques; SciTech Publisihng: Edison, NJ, USA, 2013; pp. 337–398. [Google Scholar]
- Goldshtein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci. 1988, 23, 713–720. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimkin, P.E.; Baskakov, A.I.; Komarov, A.A.; Ka, M.-H. Safe Helicopter Landing on Unprepared Terrain Using Onboard Interferometric Radar. Sensors 2020, 20, 2422. https://doi.org/10.3390/s20082422
Shimkin PE, Baskakov AI, Komarov AA, Ka M-H. Safe Helicopter Landing on Unprepared Terrain Using Onboard Interferometric Radar. Sensors. 2020; 20(8):2422. https://doi.org/10.3390/s20082422
Chicago/Turabian StyleShimkin, Pavel E., Alexander I. Baskakov, Aleksey A. Komarov, and Min-Ho Ka. 2020. "Safe Helicopter Landing on Unprepared Terrain Using Onboard Interferometric Radar" Sensors 20, no. 8: 2422. https://doi.org/10.3390/s20082422
APA StyleShimkin, P. E., Baskakov, A. I., Komarov, A. A., & Ka, M.-H. (2020). Safe Helicopter Landing on Unprepared Terrain Using Onboard Interferometric Radar. Sensors, 20(8), 2422. https://doi.org/10.3390/s20082422




