Very Short-Term Surface Solar Irradiance Forecasting Based On FengYun-4 Geostationary Satellite
Abstract
:1. Introduction
2. Measurements
2.1. Satellite Images
2.2. Ground-Based Observations
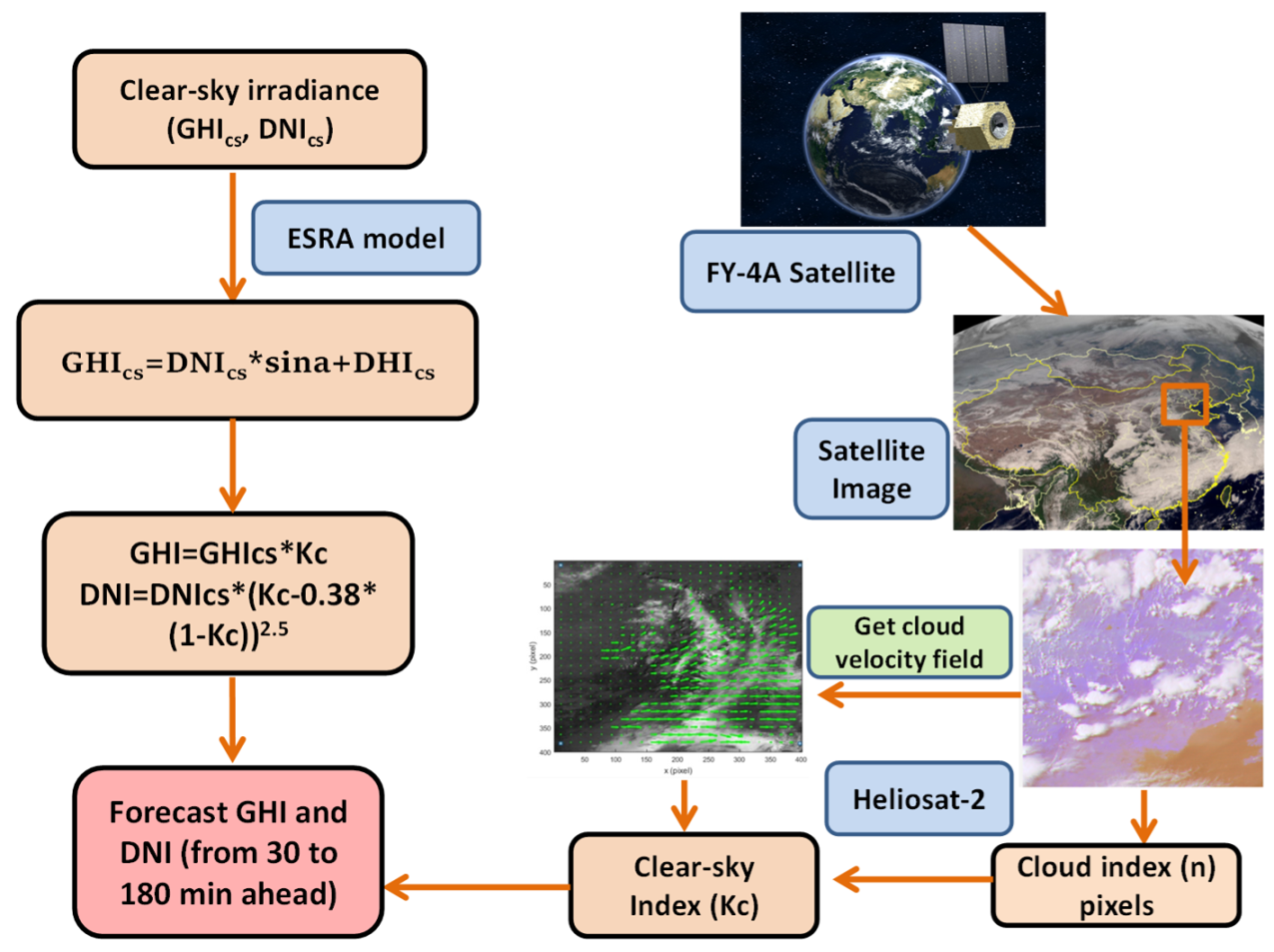
3. The Description of Forecasting Methods
3.1. ESRA Model
3.2. The Heliosat-2 Method
3.3. Forecasting Model Process
3.4. Performance Metrics
3.5. Forecast Skill
4. Results and Discussion
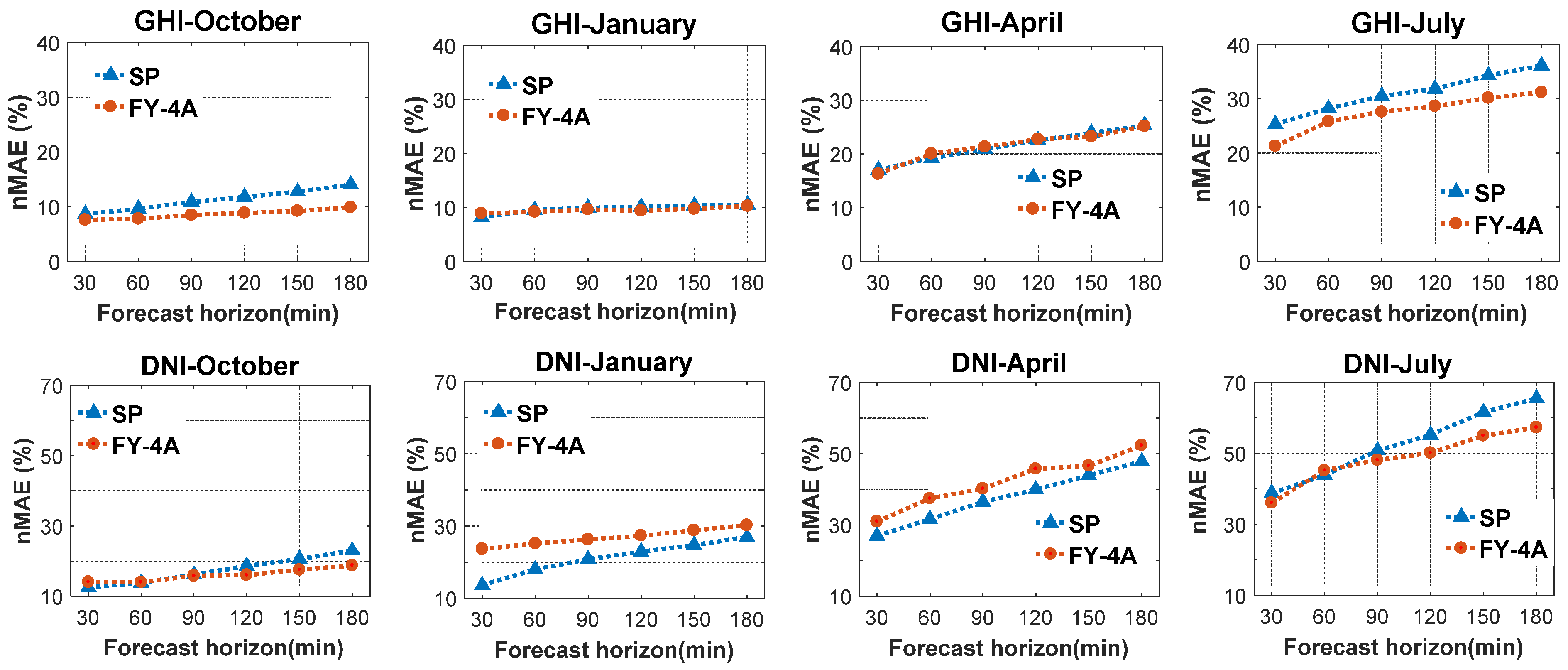
4.1. Seasonal Studies
4.1.1. Global Horizontal Solar Irradiation: GHI
4.1.2. Direct Normal Solar Irradiance (DNI)
4.1.3. Skill Value for GHI and DNI
4.2. Annual Performances
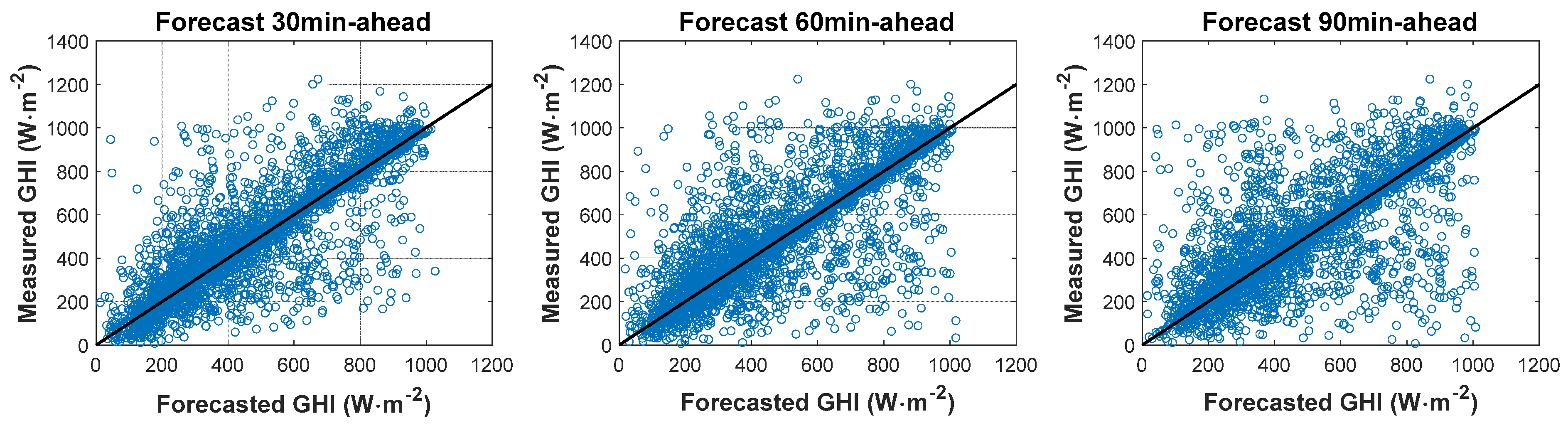
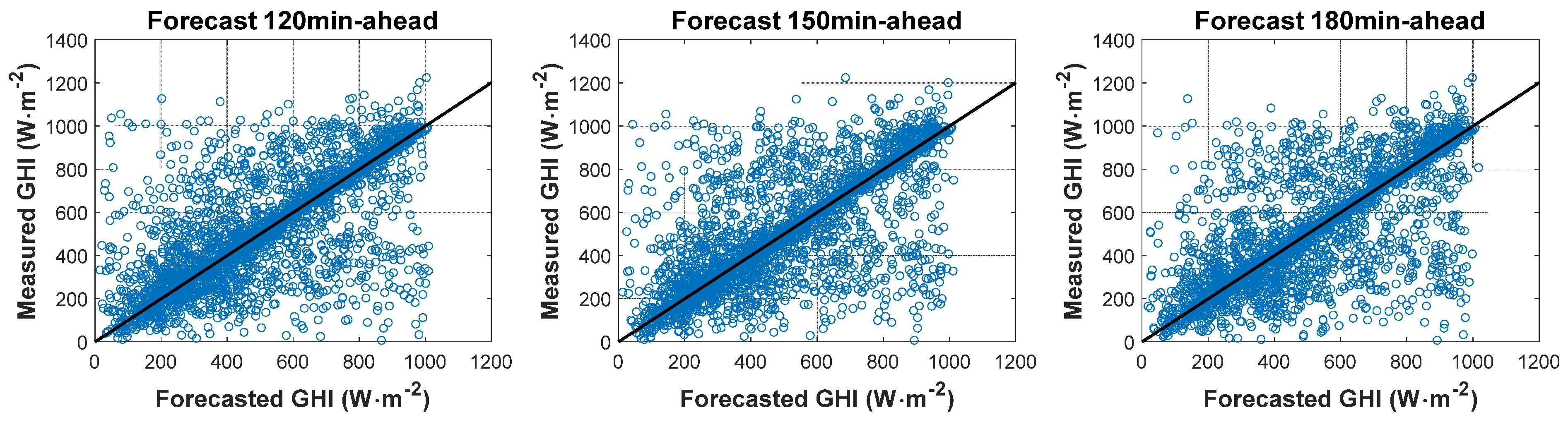
4.2.1. Forecast against Ground Measurements: GHI
4.2.2. Forecast against Ground Measurements: DNI
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, D.; Shiroyama, H. Development of photovoltaic power generation in China: A transition perspective. Renew. Sustain. Energy Rev. 2013, 25, 782–792. [Google Scholar] [CrossRef]
- Sinke, W.C. Development of photovoltaic technologies for global impact. Renew. Energy 2019, 138, 911–914. [Google Scholar] [CrossRef]
- Hanfang, L.; Lin, H.; Tan, Q.; Wu, P.; Wang, C.; Gejirifu, D.; Huang, L. Research on the policy route of China’s distributed photovoltaic power generation. Energy Rep. 2020, 6, 254–263. [Google Scholar] [CrossRef]
- Barbieri, F.; Rajakaruna, S.; Ghosh, A. Very short-term photovoltaic power forecasting with cloud modeling: A review. Renew. Sustain. Energy Rev. 2017, 75, 242–263. [Google Scholar] [CrossRef] [Green Version]
- Son, J.; Park, Y.; Lee, J.; Kim, H. Sensorless PV Power Forecasting in Grid-Connected Buildings through Deep Learning. Sensors 2018, 18, 2529. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hernández-Callejo, L.; Gallardo-Saavedra, S.; Gómez, V.A. A review of photovoltaic systems: Design, operation and maintenance. Sol. Energy 2019, 188, 426–440. [Google Scholar] [CrossRef]
- Herrería-Alonso, S.; Suárez-González, A.; Rodríguez-Pérez, M.; Rodríguez-Rubio, R.F.; López-García, C. A Solar Altitude Angle Model for Efficient Solar Energy Predictions. Sensors 2020, 20, 1391. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wild, M.; Folini, D.; Henschel, F.; Fischer, N.; Müller, B. Projections of long-term changes in solar radiation based on CMIP5 climate models and their influence on energy yields of photovoltaic systems. Sol. Energy 2015, 116, 12–24. [Google Scholar] [CrossRef] [Green Version]
- Zou, L.; Wang, L.; Li, J.; Lu, Y.; Gong, W.; Niu, Y.; Ying, N. Global surface solar radiation and photovoltaic power from Coupled Model Intercomparison Project Phase 5 climate models. J. Clean. Prod. 2019, 224, 304–324. [Google Scholar] [CrossRef]
- Barrena, C.A.; Ruiz-Arias, J.A.; Rodríguez-Benítez, F.J.; Pozo-Vázquez, D.; Tovar-Pescador, J. Short-term solar radiation forecasting by advecting and diffusing MSG cloud index. Sol. Energy 2017, 155, 1092–1103. [Google Scholar] [CrossRef]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar radiation forecasting using artificial neural network and random forest methods: Application to normal beam, horizontal diffuse and global components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Voyant, C.; Notton, G.; Kalogirou, S.; Nivet, M.-L.; Paoli, C.; Motte, F.; Fouilloy, A. Machine learning methods for solar radiation forecasting: A review. Renew. Energy 2017, 105, 569–582. [Google Scholar] [CrossRef]
- Yeom, J.-M.; Park, S.; Chae, T.; Kim, J.-Y.; Lee, C.S. Spatial Assessment of Solar Radiation by Machine Learning and Deep Neural Network Models Using Data Provided by the COMS MI Geostationary Satellite: A Case Study in South Korea. Sensors 2019, 19, 2082. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, P.; Van Westrhenen, R.; Meirink, J.F.; Van Der Veen, S.; Knap, W. Surface solar radiation forecasts by advecting cloud physical properties derived from Meteosat Second Generation observations. Sol. Energy 2019, 177, 47–58. [Google Scholar] [CrossRef]
- Caldas, M.; Alonso-Suárez, R. Very short-term solar irradiance forecast using all-sky imaging and real-time irradiance measurements. Renew. Energy 2019, 143, 1643–1658. [Google Scholar] [CrossRef]
- Kühnert, J.; Lorenz, E.; Heinemann, D. Satellite-Based Irradiance and Power Forecasting for the German Energy Market. In Solar Energy Forecasting and Resource Assessment; Academic Press: Cambridge, MA, USA, 2013; pp. 267–297. [Google Scholar]
- Escrig, H.; Batlles, F.J.; Alonso-Montesinos, J.; Baena, F.; Bosch, J.; Salbidegoitia, I.; Burgaleta, J. Cloud detection, classification and motion estimation using geostationary satellite imagery for cloud cover forecast. Energy 2013, 55, 853–859. [Google Scholar] [CrossRef]
- Zhai, H.; Zhang, H.; Zhang, L.; Li, P. Cloud/shadow detection based on spectral indices for multi/hyperspectral optical remote sensing imagery. ISPRS J. Photogramm. Remote Sens. 2018, 144, 235–253. [Google Scholar] [CrossRef]
- Nonnenmacher, L.; Coimbra, C.F. Streamline-based method for intra-day solar forecasting through remote sensing. Sol. Energy 2014, 108, 447–459. [Google Scholar] [CrossRef]
- Gallucci, D.; Romano, F.; Cersosimo, A.; Cimini, D.; Di Paola, F.; Gentile, S.; Geraldi, E.; LaRosa, S.; Nilo, S.T.; Ricciardelli, E.; et al. Nowcasting Surface Solar Irradiance with AMESIS via Motion Vector Fields of MSG-SEVIRI Data. Remote. Sens. 2018, 10, 845. [Google Scholar] [CrossRef] [Green Version]
- Ayet, A.; Tandeo, P. Nowcasting solar irradiance using an analog method and geostationary satellite images. Sol. Energy 2018, 164, 301–315. [Google Scholar] [CrossRef] [Green Version]
- Rosiek, S.; Alonso-Montesinos, J.; Batlles, F. Online 3-h forecasting of the power output from a BIPV system using satellite observations and ANN. Int. J. Electr. Power Energy Syst. 2018, 99, 261–272. [Google Scholar] [CrossRef]
- Gao, J.; Chen, J.; Tian, X. Ensemble-learning-based Cloud Phase Classification Method for FengYun-4 Remote Sensing Images. Infrared Technol. 2020, 42, 68–74. [Google Scholar]
- Liu, Y.; Xia, J.; Shi, C.-X.; Hong, Y. An Improved Cloud Classification Algorithm for China’s FY-2C Multi-Channel Images Using Artificial Neural Network. Sensors 2009, 9, 5558–5579. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Gao, X.; Li, Z.; Jia, D. Nowcasting of Surface Solar Irradiance Using FengYun-4 Satellite Observations over China. Remote. Sens. 2019, 11, 1984. [Google Scholar] [CrossRef] [Green Version]
- Rigollier, C.; Bauer, O.; Wald, L. On the clear sky model of the ESRA—European Solar Radiation Atlas—With respect to the heliosat method. Sol. Energy 2000, 68, 33–48. [Google Scholar] [CrossRef] [Green Version]
- Rigollier, C.; Lefèvre, M.; Wald, L. The method Heliosat-2 for deriving shortwave solar radiation from satellite images. Sol. Energy 2004, 77, 159–169. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zheng, Y. The flexibility pathways for integrating renewable energy into China’s coal dominated power system: The case of Beijing-Tianjin-Hebei Region. J. Clean. Prod. 2020, 245, 118925. [Google Scholar] [CrossRef]
- Gueymard, C.A.; Ruiz-Arias, J.A. Validation of direct normal irradiance predictions under arid conditions: A review of radiative models and their turbidity-dependent performance. Renew. Sustain. Energy Rev. 2015, 45, 379–396. [Google Scholar] [CrossRef]
- Ruiz-Arias, J.A.; Gueymard, C.A. Worldwide inter-comparison of clear-sky solar radiation models: Consensus-based review of direct and global irradiance components simulated at the earth surface. Sol. Energy 2018, 168, 10–29. [Google Scholar] [CrossRef]
- Sun, X.; Bright, J.M.; Gueymard, C.A.; Acord, B.; Wang, P.; Engerer, N.A. Worldwide performance assessment of 75 global clear-sky irradiance models using Principal Component Analysis. Renew. Sustain. Energy Rev. 2019, 111, 550–570. [Google Scholar] [CrossRef]
- Behar, O.; Sbarbaro, D.; Marzo, A.; Gonzalez, M.T.; Vidal, E.F.; Moran, L. Critical analysis and performance comparison of thirty-eight (38) clear-sky direct irradiance models under the climate of Chilean Atacama Desert. Renew. Energy 2020, 153, 49–60. [Google Scholar] [CrossRef]
- Ineichen, P. Validation of models that estimate the clear sky global and beam solar irradiance. Sol. Energy 2016, 132, 332–344. [Google Scholar] [CrossRef] [Green Version]
- Ineichen, P. Conversion function between the Linke turbidity and the atmospheric water vapor and aerosol content. Sol. Energy 2008, 82, 1095–1097. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Lin, A.-W.; Qin, W.-M.; He, L.-J.; Li, X. Spatial-temporal Distribution of Aerosol Optical Depth and Its Main Influence Types in China During 1990–2017. Environ. Sci. 2019, 40, 2572–2581. [Google Scholar]
- Zheng, F.; Zhou, Z.; Liu, Y.; Zuo, X.; Zhu, W. Temporal and spatial distribution characteristics of long-term aerosol optical depth in north China plain based on MODIS data. J. Henan Univ. (Nat. Sci.) 2019, 49, 450–458. [Google Scholar]
- Guo, W. Quantitative Analysis of Spatial-Temporal Characteristics and Driving Forces of Terrestrial Aerosols in China in Nearly a Decade. Master’s Thesis, Xinjiang University, Ürümqi, China, 2019. [Google Scholar]
- Guo, C. Retrieval of Aerosol Optical Depth in Shanghai Using Remotely Sensed Data of Chinese High Resolution Satellites. Master’s Thesis, East China Normal University, Shanghai, China, 2018. [Google Scholar]
- Yang, J.; Li, Z.; Chen, X.; Li, B.; Hou, W.; Zhao, S.; Ge, B.; Ma, Y.; Zhang, Y. Retrieval system of aerosol optical depth based on high spatio-temporal resolution satellite data. J. Atmos. Environ. Opt. 2017, 13, 112–120. [Google Scholar]
- Fan, K. Inversion of Aerosol Optical Depth in Beijing-Tianjin-Hebei Region Based on GF4 Satellite Data. Master’s Thesis, YanShan University, Qinhuangdao, China, 2019. [Google Scholar]
- Alonso-Montesinos, J.; Batlles, F.; Bosch, J. Beam, diffuse and global solar irradiance estimation with satellite imagery. Energy Convers. Manag. 2015, 105, 1205–1212. [Google Scholar] [CrossRef]
- Mouhamet, D.; Tommy, A.; Primerose, A.; Laurent, L. Improving the Heliosat-2 method for surface solar irradiation estimation under cloudy sky areas. Sol. Energy 2018, 169, 565–576. [Google Scholar] [CrossRef]
- Albarelo, T.; Marie-Joseph, I.; Primerose, A.; Seyler, F.; Wald, L.; Linguet, L. Optimizing the Heliosat-II Method for Surface Solar Irradiation Estimation with GOES Images. Can. J. Remote Sens. 2015, 41, 86–100. [Google Scholar] [CrossRef]
- Bueno, L.C.; Casanova-Mateo, C.; Sanz-Justo, J.; Salcedo-Sanz, S. Machine learning regressors for solar radiation estimation from satellite data. Sol. Energy 2019, 183, 768–775. [Google Scholar] [CrossRef]
- Trentmann, J.; Pfeifroth, U. Algorithm Theoretical Basis Document Meteosat Climate Data Records of Surface Radiation SARAH-2. (2.2); Satellite Application Facility on Climate Monitoring (CM SAF). 2017; Available online: https://icdc.cen.uni-hamburg.de/fileadmin/user_upload/icdc_Dokumente/EUMETSAT-CMSAF/SAF_CM_DWD_ATBD_METEOSAT_HEL_2_2.pdf (accessed on 2 May 2020).
- Skartveit, A.; Olseth, J.A.; Tuft, M.E. An hourly diffuse fraction model with correction for variability and surface albedo. Sol. Energy 1998, 63, 173–183. [Google Scholar] [CrossRef]
- Mori, N.; Chang, K.-A. Introduction to Mpiv, User Manual and Program. Available online: http://www.oceanwave.jp/softwares/mpiv/ (accessed on 2 May 2020).
- Gallucci, D.; Romano, F.; Cimini, D.; Di Paola, F.; Gentile, S.; LaRosa, S.; Nilo, S.T.; Ricciardelli, E.; Ripepi, E.; Viggiano, M.; et al. Improvement of Hourly Surface Solar Irradiance Estimation Using MSG Rapid Scanning Service. Remote Sens. 2019, 11, 66. [Google Scholar] [CrossRef] [Green Version]
- Kleissl, J. Solar Energy Forecasting and Resource Assessment; Academic Press: Cambridge, MA, USA, 2013; pp. 171–194. [Google Scholar]
- Dong, J.; Olama, M.M.; Kuruganti, T.; Melin, A.M.; Djouadi, S.M.; Zhang, Y.; Xue, Y. Novel stochastic methods to predict short-term solar radiation and photovoltaic power. Renew. Energy 2020, 145, 333–346. [Google Scholar] [CrossRef]
- Voyant, C.; Soubdhan, T.; Lauret, P.; David, M.; Muselli, M. Statistical parameters as a means to a priori assess the accuracy of solar forecasting models. Energy 2015, 90, 671–679. [Google Scholar] [CrossRef] [Green Version]
- Márquez, R.; Coimbra, C.F. Proposed Metric for Evaluation of Solar Forecasting Models. J. Sol. Energy Eng. 2012, 135, 011016. [Google Scholar] [CrossRef] [Green Version]
- Letu, H.; Yang, K.; Nakajima, T.Y.; Ishimoto, H.; Nagao, T.M.; Riedi, J.; Baran, A.J.; Ma, R.; Wang, T.; Shang, H.; et al. High-resolution retrieval of cloud microphysical properties and surface solar radiation using Himawari-8/AHI next-generation geostationary satellite. Remote Sens. Environ. 2020, 239, 111583. [Google Scholar] [CrossRef]
- Xingxing, G.; Hailin, G.; Yan, C.; Lei, Z.; Wu, Z. Spatiotemporal characteristics of aerosols and its effects on cloud and precipitation during summer over typical regions in China. J. Meteorol. Environ. 2020, 36, 11–20. [Google Scholar]
- Zhao, J.; Xu, H.; Kong, X.; Guo, J.; Xu, J.; Yu, W. Estimating Surface Direct Radiation Effect of Aerosol Based on MODIS and AERONET Data. Chin. J. Agrometeorol. 2018, 39, 693–701. [Google Scholar]





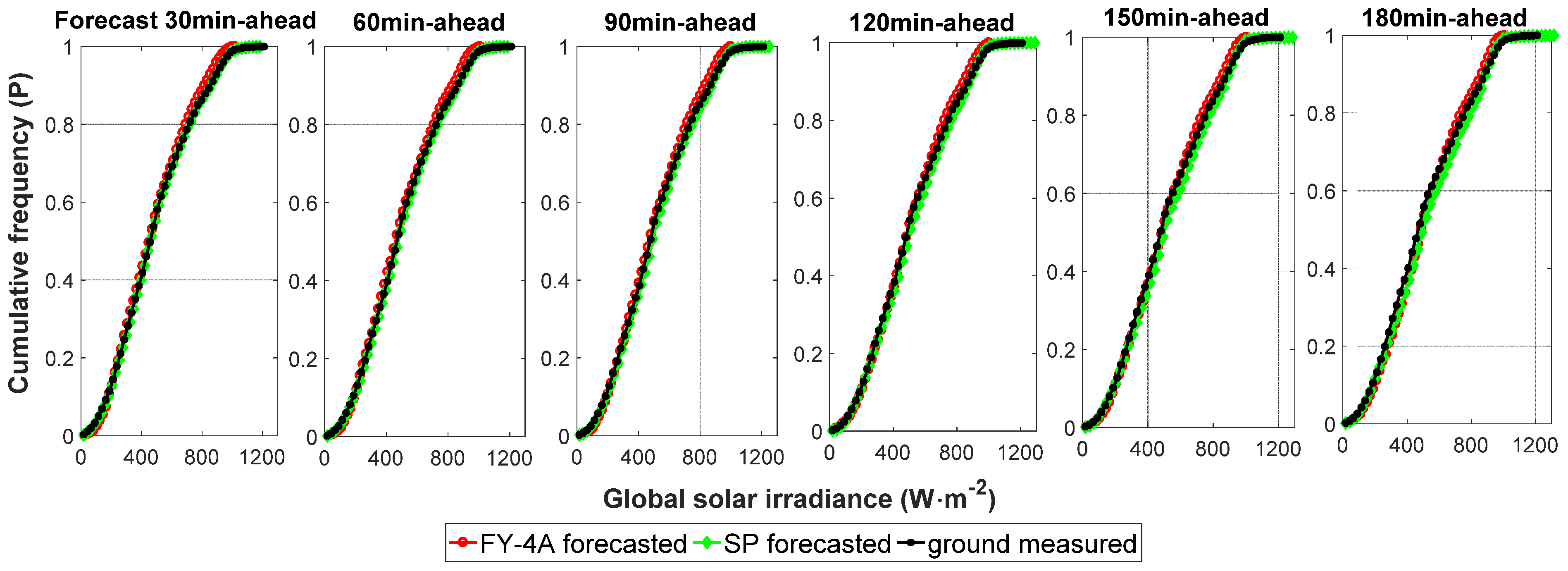
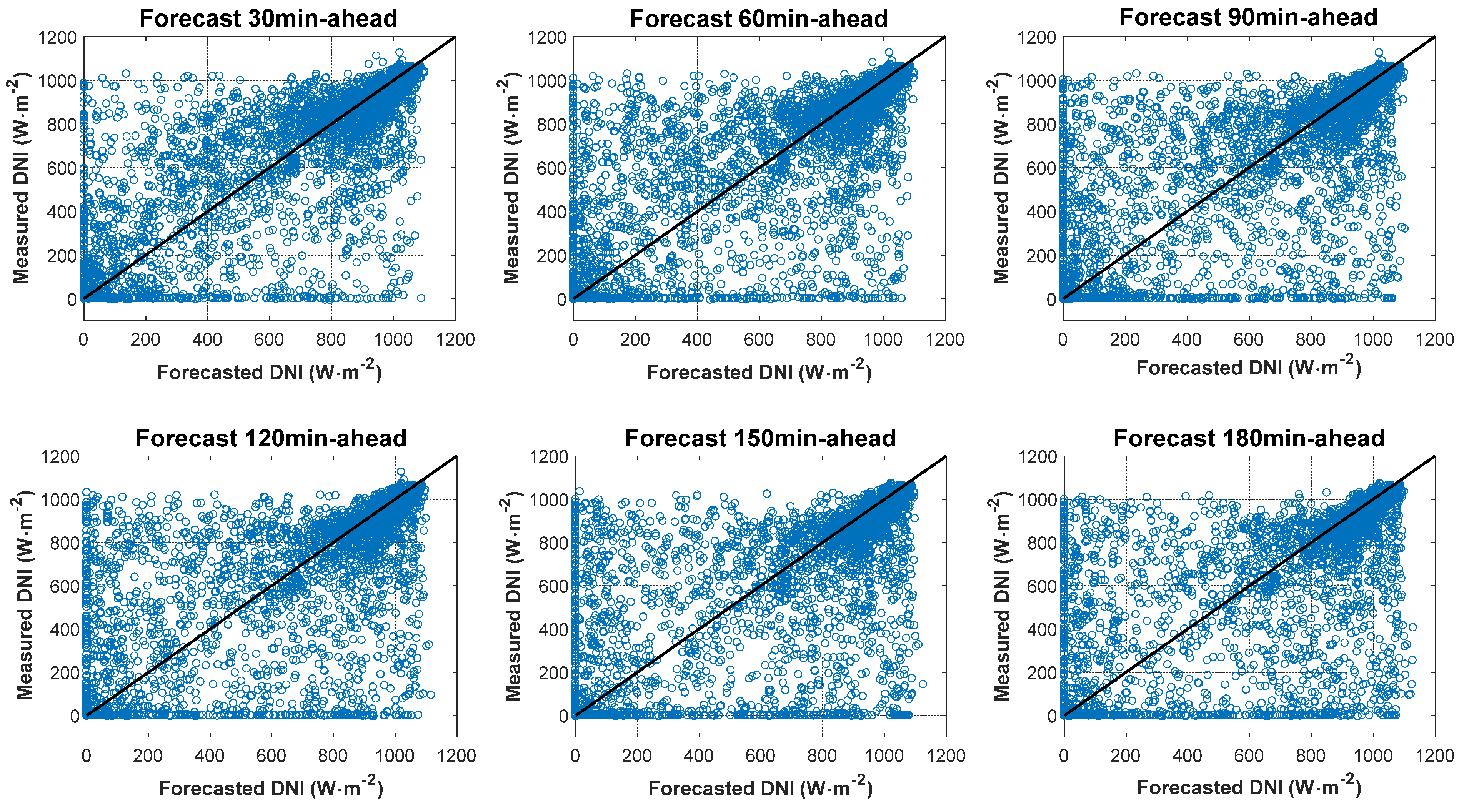

| Metric | Model | 30 min | 60 min | 90 min | 120 min | 150 min | 180 min |
|---|---|---|---|---|---|---|---|
| Mean value | 493.94 | 504.67 | 511.89 | 516.60 | 517.68 | 514.11 | |
| RMSE | SP | 166.09 | 180.93 | 190.30 | 200.08 | 209.11 | 215.73 |
| FY-4A | 132.29 | 159.04 | 172.75 | 179.41 | 184.94 | 189.44 | |
| nRMSE (%) | SP | 33.66 | 35.89 | 37.22 | 38.80 | 40.50 | 42.04 |
| FY-4A | 26.78 | 31.51 | 33.74 | 34.73 | 35.72 | 36.84 | |
| MAE | SP | 81.96 | 94.58 | 103.26 | 110.03 | 117.65 | 123.41 |
| FY-4A | 73.54 | 88.75 | 96.07 | 100.95 | 104.81 | 109.79 | |
| nMAE (%) | SP | 16.61 | 18.76 | 20.20 | 21.34 | 22.79 | 24.05 |
| FY-4A | 14.88 | 17.58 | 18.76 | 19.54 | 20.24 | 21.35 | |
| MBE | SP | 5.15 | 8.31 | 12.08 | 15.38 | 19.42 | 24.24 |
| FY-4A | −10.33 | −10.19 | −8.08 | −5.16 | −2.32 | 5.67 | |
| nMBE (%) | SP | 1.04 | 1.65 | 2.36 | 2.98 | 3.76 | 4.72 |
| FY-4A | −2.09 | −2.02 | −1.57 | −1.00 | −0.45 | 1.10 | |
| R | SP | 0.77 | 0.73 | 0.70 | 0.68 | 0.66 | 0.65 |
| FY-4A | 0.85 | 0.78 | 0.74 | 0.73 | 0.72 | 0.71 | |
| SS (%) | FY-4A | 20.44 | 12.20 | 9.35 | 10.49 | 11.80 | 12.37 |
| Metric | Model | 30 min | 60 min | 90 min | 120 min | 150 min | 180 min |
|---|---|---|---|---|---|---|---|
| Mean value | 586.00 | 592.98 | 594.57 | 594.17 | 592.17 | 588.47 | |
| RMSE | SP | 255.55 | 284.52 | 308.61 | 331.11 | 352.76 | 370.41 |
| FY-4A | 240.01 | 278.61 | −296.76 | 315.33 | 330.51 | 346.05 | |
| nRMSE (%) | SP | 43.67 | 47.17 | 52.11 | 55.86 | 59.67 | 62.97 |
| FY-4A | 40.96 | 46.98 | 50.03 | 53.04 | 55.81 | 58.80 | |
| MAE | SP | 130.71 | 156.67 | 178.39 | 196.53 | 215.94 | 231.97 |
| FY-4A | 148.43 | 173.99 | 186.87 | 199.70 | 211.52 | 224.51 | |
| nMAE (%) | SP | 22.34 | 26.53 | 30.12 | 33.16 | 36.53 | 39.43 |
| FY-4A | 25.33 | 29.34 | 31.50 | 33.59 | 35.72 | 38.15 | |
| MBE | SP | 20.02 | 27.96 | 38.14 | 47.85 | 59.69 | 73.37 |
| FY-4A | 5.51 | 5.34 | 16.68 | 22.52 | 36.02 | 50.39 | |
| nMBE (%) | SP | 3.42 | 4.73 | 6.44 | 8.07 | 10.10 | 12.47 |
| FY-4A | 0.94 | 0.90 | 2.81 | 3.79 | 6.08 | 8.56 | |
| R | SP | 0.77 | 0.72 | 0.67 | 0.62 | 0.58 | 0.54 |
| FY-4A | 0.80 | 0.73 | 0.70 | 0.66 | 0.63 | 0.60 | |
| SS (%) | FY-4A | 6.20 | 0.40 | 3.99 | 5.05 | 6.47 | 6.62 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Gao, X.; Hua, J.; Wu, P.; Li, Z.; Jia, D. Very Short-Term Surface Solar Irradiance Forecasting Based On FengYun-4 Geostationary Satellite. Sensors 2020, 20, 2606. https://doi.org/10.3390/s20092606
Yang L, Gao X, Hua J, Wu P, Li Z, Jia D. Very Short-Term Surface Solar Irradiance Forecasting Based On FengYun-4 Geostationary Satellite. Sensors. 2020; 20(9):2606. https://doi.org/10.3390/s20092606
Chicago/Turabian StyleYang, Liwei, Xiaoqing Gao, Jiajia Hua, Pingping Wu, Zhenchao Li, and Dongyu Jia. 2020. "Very Short-Term Surface Solar Irradiance Forecasting Based On FengYun-4 Geostationary Satellite" Sensors 20, no. 9: 2606. https://doi.org/10.3390/s20092606
APA StyleYang, L., Gao, X., Hua, J., Wu, P., Li, Z., & Jia, D. (2020). Very Short-Term Surface Solar Irradiance Forecasting Based On FengYun-4 Geostationary Satellite. Sensors, 20(9), 2606. https://doi.org/10.3390/s20092606





