Effectiveness of Non-Local Means Algorithm with an Industrial 3 MeV LINAC High-Energy X-ray System for Non-Destructive Testing
Abstract
:1. Introduction
2. Materials and Methods
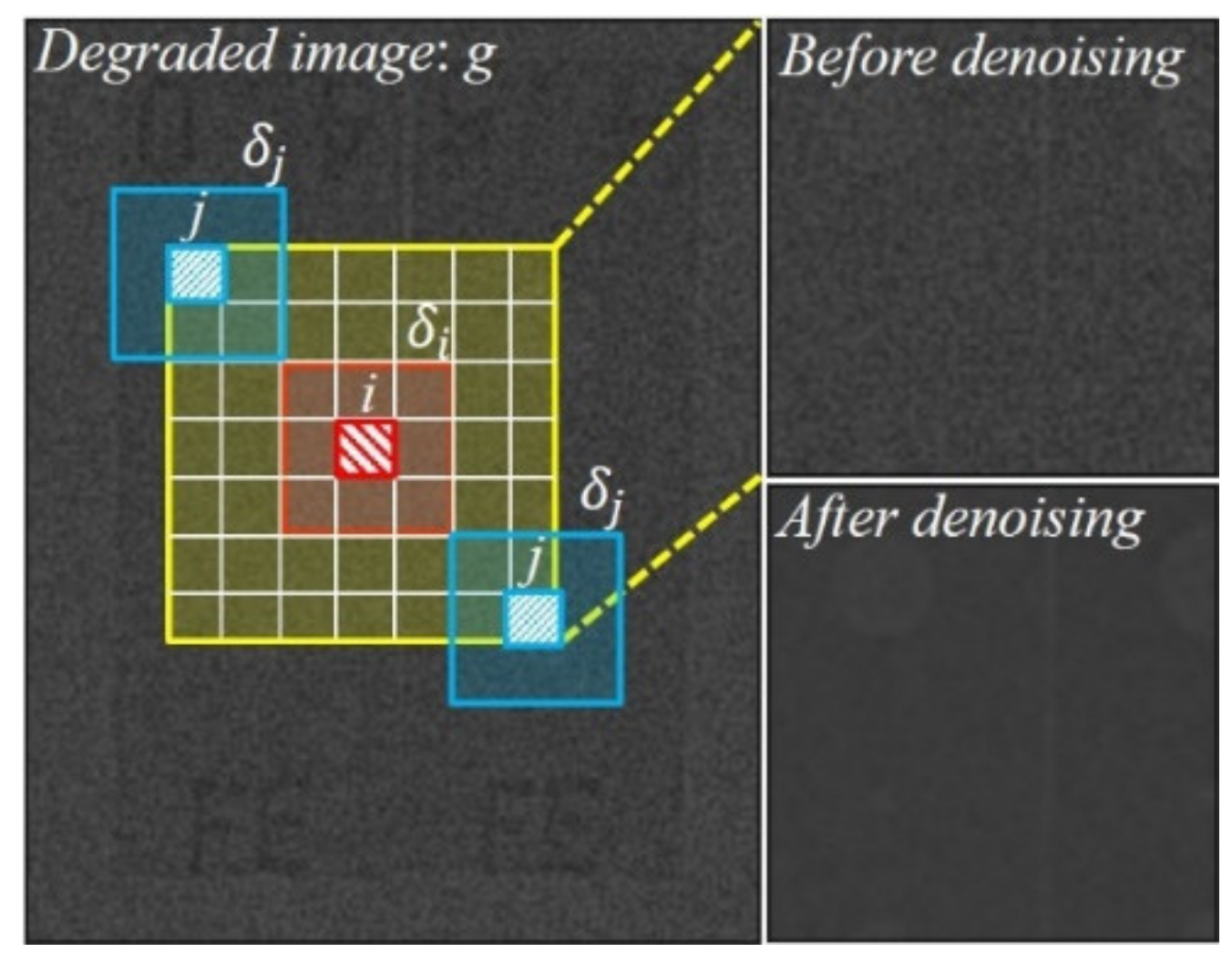
2.1. Modeling the Proposed NLM Denoising Algorithm
2.2. Industrial High-Energy X-ray Imaging System and Materials Modeling
2.3. Evaluation of Image Quality
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kruth, J.P.; Bartscher, M.; Carmignato, S. Computed tomography for dimensional metrology. CIRP Ann. Manuf. Technol. 2011, 60, 821–842. [Google Scholar] [CrossRef]
- Aryan, P.; Sampath, S.; Sohn, H. An overview of non-destructive testing methods for integrated circuit packaging inspection. Sensors 2018, 18, 1981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Katunin, A.; Wronkowicz-Katunin, A.; Dragan, K. Impact damage evaluation in composite structures based on fusion of results of ultrasonic testing and X-ray computed tomography. Sensors 2020, 20, 1867. [Google Scholar] [CrossRef] [Green Version]
- Chiffre, L.D.; Carmignato, S.; Kruth, J.P.; Schmitt, R.; Weckenmann, A. Industrial applications of computed tomography. CIRP Ann. Manuf. Technol. 2014, 63, 655–677. [Google Scholar] [CrossRef]
- Takagi, H.; Murata, I. Energy spectrum measurement of high power and high energy (6 and 9 MeV) pulsed X-ray source for industrial use. J. Radiat. Prot. Res. 2016, 41, 93–99. [Google Scholar] [CrossRef]
- Wu, Y.C.; Zhu, B.; Li, G.; Zhang, X.H.; Yu, M.H.; Dong, K.G.; Zhang, T.K.; Yang, Y.; Bi, B.; Yang, J.; et al. Towards high-energy, high-resolution computed tomography via a laser driven micro-spot gamma-ray source. Sci. Rep. 2018, 8, 15888. [Google Scholar] [CrossRef] [Green Version]
- Zhu, L.; Wang, J.; Xing, L. Noise suppression in scatter correction for cone-beam CT. Med. Phys. 2009, 36, 741–752. [Google Scholar] [CrossRef] [Green Version]
- Foi, A.; Trimeche, M.; Katkovnik, V.; Egiazarian, K. Practical poissonian-gaussian noise modeling and fitting for single-image raw-data. IEEE Trans. Image Process. 2008, 17, 1737–1754. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Lee, M.S.; Kang, M.G. Poisson-gaussian noise analysis and estimation for low-dose x-ray images in the NSCT domain. Sensors 2018, 18, 1019. [Google Scholar]
- Kirti, T.; Jitendra, K.; Ashok, S. Poisson noise reduction from X-ray images by region classification and response median filtering. Sādhanā 2017, 42, 855–863. [Google Scholar] [CrossRef] [Green Version]
- Cadena, L.; Zotin, A.; Cadena, F.; Espinosa, N. Noise removal of the x-ray medical image using fast spatial filters and GPU. In Proceedings of the SPIE 10752, Applications of Digital Image Processing XLI, San Diego, CA, USA, 17 September 2018. [Google Scholar]
- Wang, L.; Lu, J.; Li, Y.; Yahagi, T.; Okamoto, T. Noise reduction using wavelet with application to medical x-ray image. In Proceedings of the 2015 IEEE International Conference on Industrial Technology, Hong Kong, China, 14–17 December 2005; pp. 33–38. [Google Scholar]
- Makitalo, M.; Foi, A. Optimal inversion of the anscombe transformation in low-count poisson image denoising. IEEE Trans. Image Process. 2010, 20, 99–109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makitalo, M.; Foi, A. A closed-form approximation of the exact unbiased inverse of the anscombe variance-stabilizing transformation. IEEE Trans. Image Process. 2011, 20, 2697–2698. [Google Scholar] [CrossRef] [PubMed]
- Osher, S.; Burger, M.; Goldfarb, D.; Xu, J.; Yin, W. An iterative regularization method for total variation-based image restoration. Multiscale Model. Simul. 2005, 4, 460–489. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Physica D 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, L.; Zuo, W.; Zhang, D.; Feng, X. Patch group based nonlocal self-similarity prior learning for image denoising. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 244–252. [Google Scholar]
- Zhang, H.; Ouyang, L.; Huang, J.; Ma, J.; Chen, W.; Wang, J. Few-view cone-beam CT reconstruction with deformed prior image. Med. Phys. 2014, 41, 121905. [Google Scholar] [CrossRef]
- Sattar, F.; Floreby, L.; Salomonsson, G.; Lovstrom, B. Image enhancement based on a nonlinear multiscale method. IEEE Trans. Image Process. 1997, 6, 888–895. [Google Scholar] [CrossRef]
- Koutalonis, M.; Delis, H.; Spyrou, G.; Costaridou, L.; Tzanakos, G.; Panayiotakis, G. Contrast-to-noise ratio in magnification mammography: A monte carlo study. Phys. Med. Biol. 2007, 52, 3185–3199. [Google Scholar] [CrossRef]
- Lee, J.H.; Kim, Y.R.; Lee, G.M.; Ryu, J.H.; Cho, E.Y.; Lee, Y.H.; Yoon, K.H. Coefficient of variation on Gd-EOB MR imaging: Correlation with the presence of early-stage hepatocellular carcinoma in patients with chronic hepatitis B. Eur. J. Radiol. 2018, 102, 95–101. [Google Scholar] [CrossRef]
- Williams, M.B.; Mangiafico, P.A.; Simoni, P.U. Noise power spectra of images from digital mammography detectors. Med. Phys. 1999, 26, 1279–1293. [Google Scholar] [CrossRef]
- Kim, D.S.; Kim, E. Noise power spectrum of the fixed pattern noise in digital radiography detectors. Med. Phys. 2016, 43, 2765–2773. [Google Scholar] [CrossRef]
- Diwakar, M.; Kumar, M. Edge preservation based CT image denoising using wiener filtering and thresholding in wavelet domain. In Proceedings of the 2016 Fourth International Conference on Parallel, Distributed and Grid Computing (PDGC), Waknaghat, India, 22–24 December 2016; pp. 332–336. [Google Scholar]
- Agrad, D.A.; Hiraoka, Y.; Shaw, P.; Sedat, J.W. Fluorescence microscopy in three dimensions. Methods Cell Biol. 1989, 30, 353–377. [Google Scholar]
- Lu, H.; Wei, J.; Liu, Q.; Wang, Y.; Deng, X. A dictionary learning method with total generalized variation for MRI reconstruction. Int. J. Biomed. Imaging 2016, 2016, 7512471. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shim, J.; Yoon, M.; Lee, Y. Feasibility of fast non local means filter in pediatric chest x-ray for increasing of pulmonary nodule detectability with 3D printed lung nodule phantom. J. Radiol. Prot. 2019, 39, 872–889. [Google Scholar] [CrossRef] [PubMed]









| Categories | Values |
|---|---|
| Focal spot size | 2 mm |
| Beam angle | 0–23° |
| Beam symmetry | 5% |
| Dose rate | 3.0 Gy/min@1m |
| Noise Reduction Method | RMSE | EPI |
|---|---|---|
| Noisy image | 38.7 | 0.17 |
| Wiener filter | 12.5 | 0.3 |
| Total variation | 6.5 | 0.74 |
| Non-local means | 1.2 | 0.87 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Choi, J.; Lee, Y. Effectiveness of Non-Local Means Algorithm with an Industrial 3 MeV LINAC High-Energy X-ray System for Non-Destructive Testing. Sensors 2020, 20, 2634. https://doi.org/10.3390/s20092634
Kim K, Choi J, Lee Y. Effectiveness of Non-Local Means Algorithm with an Industrial 3 MeV LINAC High-Energy X-ray System for Non-Destructive Testing. Sensors. 2020; 20(9):2634. https://doi.org/10.3390/s20092634
Chicago/Turabian StyleKim, Kyuseok, Jaegu Choi, and Youngjin Lee. 2020. "Effectiveness of Non-Local Means Algorithm with an Industrial 3 MeV LINAC High-Energy X-ray System for Non-Destructive Testing" Sensors 20, no. 9: 2634. https://doi.org/10.3390/s20092634
APA StyleKim, K., Choi, J., & Lee, Y. (2020). Effectiveness of Non-Local Means Algorithm with an Industrial 3 MeV LINAC High-Energy X-ray System for Non-Destructive Testing. Sensors, 20(9), 2634. https://doi.org/10.3390/s20092634




