Design Rule of Mach-Zehnder Interferometer Sensors for Ultra-High Sensitivity
Abstract
:1. Introduction
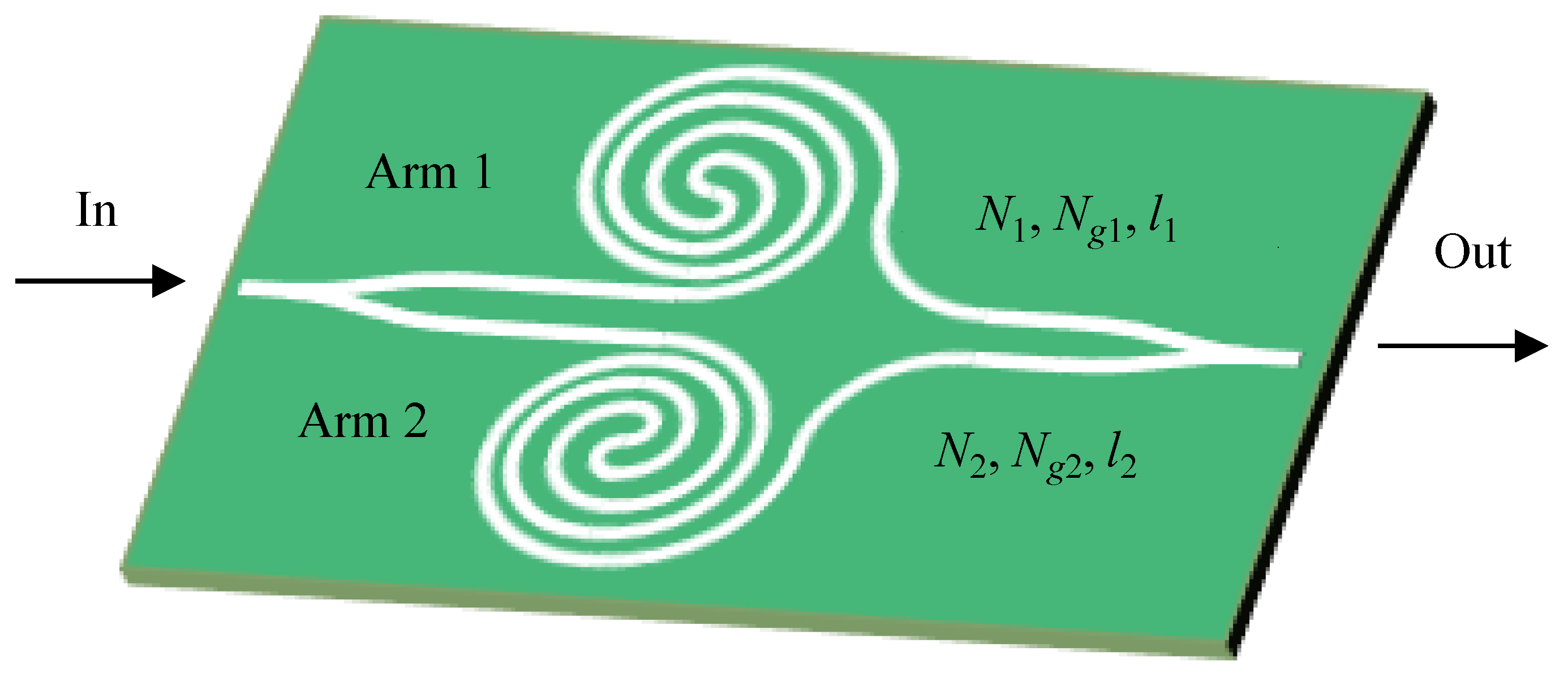
2. Principle
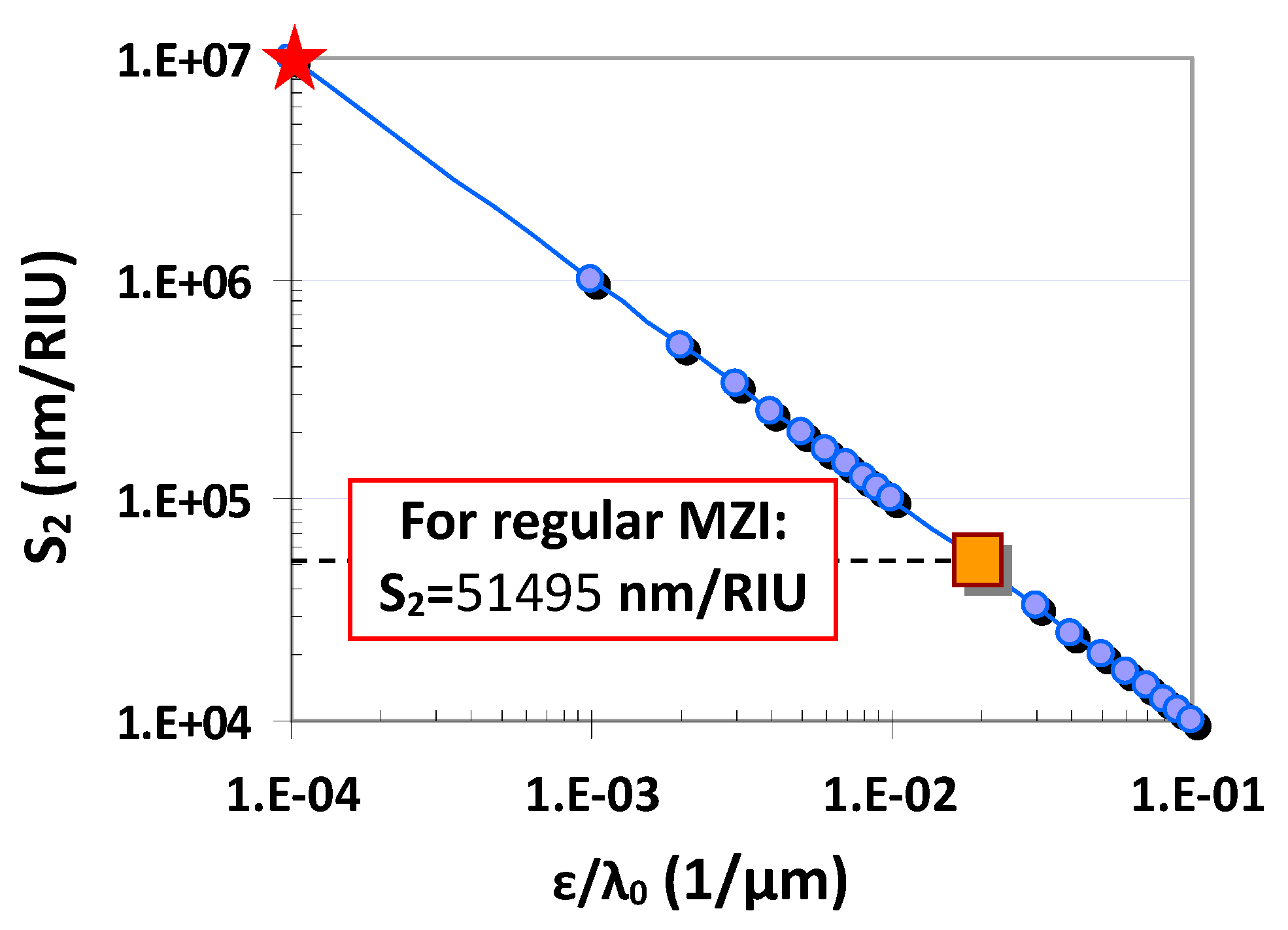
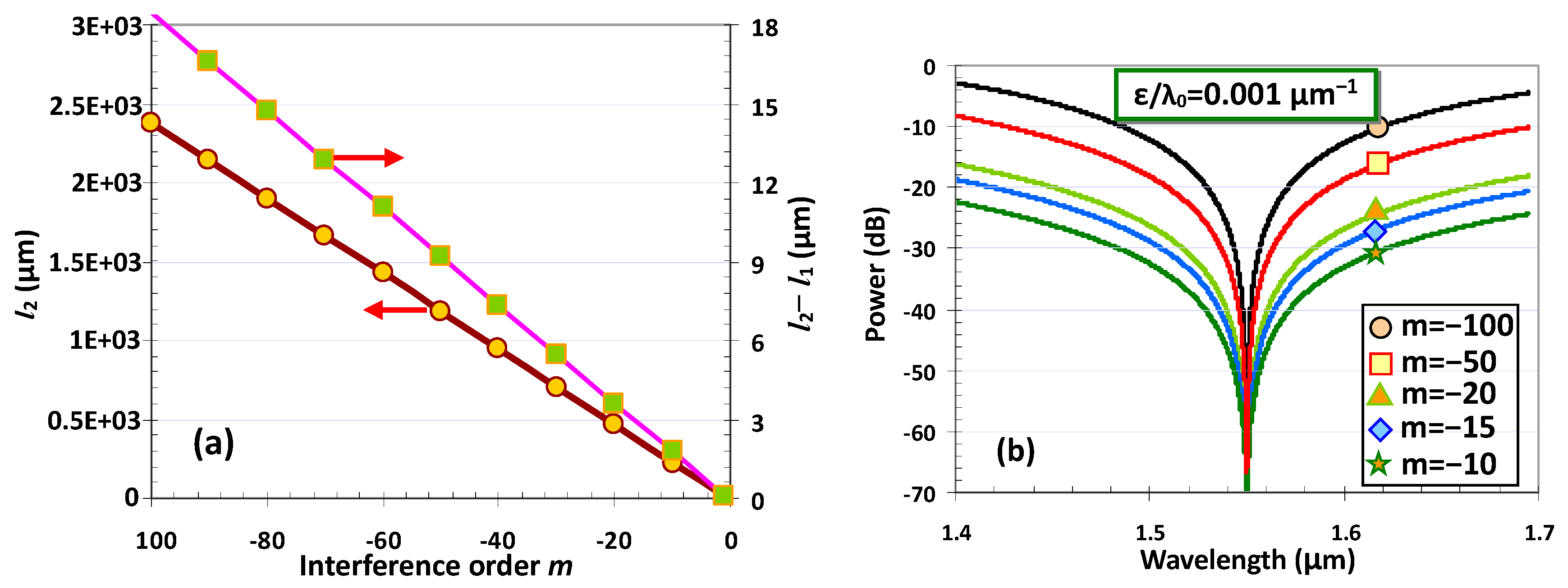
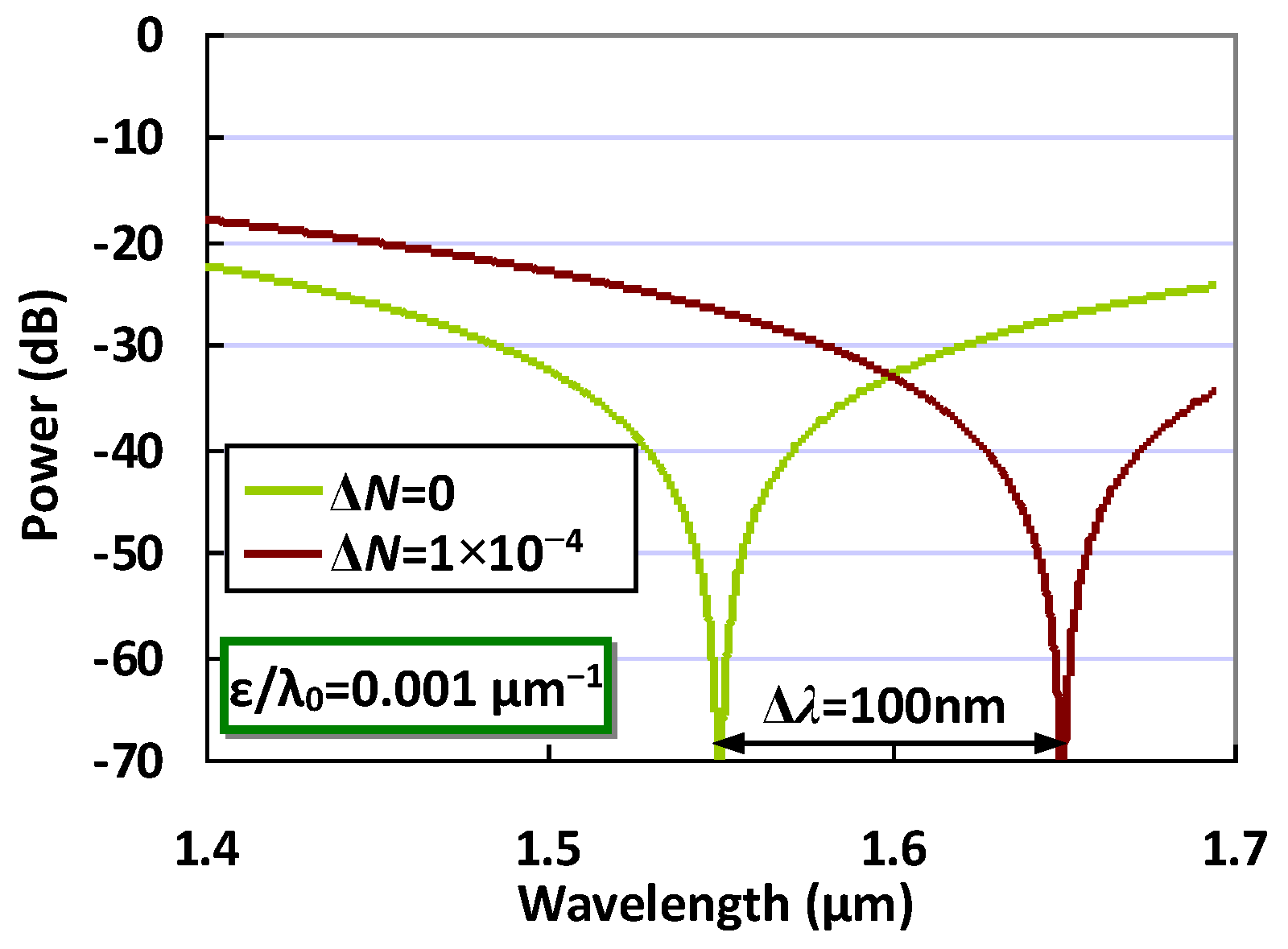
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Densmore, A.; Xu, D.-X.; Waldron, P.; Janz, S.; Cheben, P.; Lapointe, J.; Delâge, A.; Lamontagne, B.; Schmid, J.H.; Post, E. A silicon-on-insulator photonic wire based evanescent field sensor. IEEE Photon. Technol. Lett. 2006, 18, 2520–2522. [Google Scholar] [CrossRef]
- Nemova, G.; Kashyap, R. Theoretical model of a planar integrated refractive index sensor based on surface plasmon-polariton excitation with a long period grating. J. Opt. Soc. Am. B 2007, 24, 2696–2701. [Google Scholar] [CrossRef]
- Cho, S.-Y.; Jokerst, N.M. A polymer microdisk photonic sensor integrated onto silicon. IEEE Photon. Technol. Lett. 2006, 18, 2096–2098. [Google Scholar] [CrossRef]
- Chao, C.-Y.; Guo, L.J. Biochemical sensors based on polymer microrings with sharp asymmetrical resonance. Appl. Phys. Lett. 2003, 83, 1527–1529. [Google Scholar] [CrossRef]
- Xu, Q.; Almeida, V.R.; Panepucci, R.R.; Lipson, M. Experimental demonstration of guiding and confining light in nanometer-size low-refractive-index material. Opt. Lett. 2004, 29, 1626–1628. [Google Scholar] [CrossRef]
- Xu, D.-X.; Densmore, A.; Delâge, A.; Waldron, P.; McKinnon, R.; Janz, S.; Lapointe, J.; Lopinski, G.; Mischki, T.; Post, E.; et al. Folded cavity SOI microring sensors for high sensitivity and real time measurement of biomolecular binding. Opt. Express 2008, 16, 15137–15148. [Google Scholar] [CrossRef]
- Armani, A.M.; Kulkarni, R.P.; Fraser, S.E.; Flagan, R.C.; Vahala, K.J. Label-free, single-molecule detection with optical microcavities. Science 2007, 317, 783–787. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Guo, L.J. Optical sensors based on active microcavities. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 143–147. [Google Scholar] [CrossRef]
- Li, M.; Cushing, S.K.; Wu, N. Plasmon-enhanced optical sensors: A review. Analyst 2015, 140, 386–406. [Google Scholar] [CrossRef] [Green Version]
- Liao, Z.; Zhang, Y.; Li, Y.; Miao, Y.; Gao, S.; Lin, F.; Deng, Y.; Geng, L. Microfluidic chip coupled with optical biosensors for simultaneous detection of multiple analytes: A review. Biosens. Bioelectron. 2019, 126, 697–706. [Google Scholar] [CrossRef]
- Kumar, M.; Kumar, A.; Dwivedi, R. Ultra high sensitive integrated optical waveguide refractive index sensor based on multimode interference. Sens. Actuators B Chem. 2016, 222, 556–561. [Google Scholar] [CrossRef]
- Zhao, N.; Qian, G.; Fu, X.C.; Zhang, L.J.; Hu, W.; Li, R.Z.; Zhang, T. Integrated optical displacement sensor based on asymmetric Mach–Zehnder interferometer chip. Opt. Eng. 2017, 56, 027109. [Google Scholar] [CrossRef]
- Kim, H.T.; Yu, M. Cascaded ring resonator-based temperature sensor with simultaneously enhanced sensitivity and range. Opt. Express 2016, 24, 9501–9510. [Google Scholar] [CrossRef] [PubMed]
- Chao, C.-Y.; Guo, L.J. Design and optimization of microring resonators in biochemical sensing applications. J. Lightwave Technol. 2006, 24, 1395–1402. [Google Scholar] [CrossRef]
- Dai, D. Highly sensitive digital optical sensor based on cascaded high-Q ring-resonators. Opt. Express 2009, 17, 23817–23822. [Google Scholar] [CrossRef]
- Jin, L.; Li, M.; He, J. Highly-sensitive silicon-on-insulator sensor based on two cascaded micro-ring resonators with vernier effect. Opt. Commun. 2011, 284, 156–159. [Google Scholar] [CrossRef]
- Hu, J.; Dai, D. Cascaded-ring optical sensor with enhanced sensitivity by using suspended Si-nanowires. IEEE Photon. Technol. Lett. 2011, 23, 842–844. [Google Scholar]
- Qin, L.; Wang, L.; Li, M.; He, J. Optical sensor based on vernier-cascade of ring resonator and echelle diffraction grating. IEEE Photon. Technol. Lett. 2012, 24, 954–956. [Google Scholar] [CrossRef]
- Yi, H.; Citrin, D.; Chen, Y.; Zhou, Z. Dual-microring-resonator interference sensor. Appl. Phys. Lett. 2009, 95, 191112. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.; Li, M.; He, J.J. High-sensitivity and wide-range optical sensor based on three cascaded ring resonators. Opt. Express 2017, 25, 972–978. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.Y.; Liao, J.X.; Zhang, L. Vernier effect of cascaded dual microring sensor. Pramana 2018, 91, 81. [Google Scholar] [CrossRef]
- Chen, C.; Hou, X.; Si, J. Protein analysis by Mach-Zehnder interferometers with a hybrid plasmonic waveguide with nano-slots. Opt. Express 2017, 25, 31294–31308. [Google Scholar] [CrossRef]
- Xu, S.; Thylén, L.; Lech, W. Hollow hybrid plasmonic mach–zehnder sensor. Opt. Lett. 2017, 42, 807–810. [Google Scholar]
- Jiang, X.; Chen, Y.; Yu, F.; Tang, L.; Li, M.; He, J.J. High-sensitivity optical biosensor based on cascaded Mach–Zehnder interferometer and ring resonator using Vernier effect. Opt. Lett. 2014, 39, 6363–6366. [Google Scholar] [CrossRef] [PubMed]
- Chatzianagnostou, E.; Manolis, A.; Dabos, G.; Ketzaki, D.; Miliou, A.; Pleros, N.; Markey, L.; Weeber, J.; Dereux, A.; Chmielak, B.; et al. Scaling the Sensitivity of Integrated Plasmo-Photonic Interferometric Sensors. ACS Photonics 2019, 6, 1664–1673. [Google Scholar] [CrossRef]
- Martens, D.; Ramirez-Priego, P.; Murib, M.S.; Elamin, A.A.; Gonzalez-Guerrero, A.B.; Stehr, M.; Jonas, F.; Anton, B.; Hlawatsch, N.; Soetaert, P.; et al. A low-cost integrated biosensing platform based on SiN nanophotonics for biomarker detection in urine. Anal. Methods 2018, 10, 3066–3073. [Google Scholar] [CrossRef] [Green Version]
- Kitsara, M.; Misiakos, K.; Raptis, I.; Makarona, E. Integrated optical frequency-resolved Mach-Zehnder interferometers for label-free affinity sensing. Opt. Express 2010, 18, 8193–9206. [Google Scholar] [CrossRef]
- Xia, Z.; Chen, Y.; Zhou, Z. Dual waveguide coupled microring resonator sensor based on intensity detection. IEEE J. Quantum Electron. 2008, 44, 100–107. [Google Scholar] [CrossRef]
- Stievater, T.; Park, D.; Rabinovich, W.; Pruessner, M.; Kanakaraju, S.; Richardson, C.; Khurgin, J. Enhanced electro-optic phase shifts in suspended waveguides. Opt. Express 2010, 18, 885–892. [Google Scholar] [CrossRef]
- Yang, B.; Sheng, Z.; Dai, D. Design of suspended SU-8 optical waveguides for ultrasmall bending. In Proceedings of the Asia Communications and Photonics conference and Exhibition (ACP), Shanghai, China, 2–6 November 2009. [Google Scholar]
- Tao, S.H.; Fang, Q.; Song, J.F.; Yu, M.B.; Kwong, D.L. Cascade wide-angle y-junction 1 × 16 optical power splitter based on silicon wire waveguides on silicon-on-insulator. Opt. Express 2008, 16, 21456–21461. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, S.; Wang, K.; Skafidas, E. Ultra-broadband and low-loss 3 db optical power splitter based on adiabatic tapered silicon waveguides. Opt. Lett. 2016, 41, 2053–2056. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Zhang, M.; Dai, D. Design Rule of Mach-Zehnder Interferometer Sensors for Ultra-High Sensitivity. Sensors 2020, 20, 2640. https://doi.org/10.3390/s20092640
Xie Y, Zhang M, Dai D. Design Rule of Mach-Zehnder Interferometer Sensors for Ultra-High Sensitivity. Sensors. 2020; 20(9):2640. https://doi.org/10.3390/s20092640
Chicago/Turabian StyleXie, Yiwei, Ming Zhang, and Daoxin Dai. 2020. "Design Rule of Mach-Zehnder Interferometer Sensors for Ultra-High Sensitivity" Sensors 20, no. 9: 2640. https://doi.org/10.3390/s20092640
APA StyleXie, Y., Zhang, M., & Dai, D. (2020). Design Rule of Mach-Zehnder Interferometer Sensors for Ultra-High Sensitivity. Sensors, 20(9), 2640. https://doi.org/10.3390/s20092640





